Cours d'apprentissage en ligne

Étude f : Niveau MPSI mais outils de première !

Le cours porte sur l'étude d'une famille de fonctions de la forme E(2x)/x^n, où n est un entier naturel non nul. Tout d'abord, il est demandé de déterminer le plus grand ensemble de définition de la fonction f. Cela est relativement simple, car il suffit d'éviter que le dénominateur soit nul. Ensuite, il est demandé de déterminer le plus grand ensemble de dérivabilité de f. Étant donné que f est le produit d'une exponentielle et d'une fraction de polynôme, f sera dérivable sur tout son ensemble de définition. Ensuite, en supposant que n est pair, il est demandé de dresser le tableau de variation de f sans indication des limites aux bornes. Pour cela, on étudie la dérivée de f, qui est obtenue en utilisant la règle du quotient. On factorise certains termes et on constate que le changement de signe se produit en 0 et en 2p. On en déduit le tableau de variation de f. Ensuite, les limites de f aux bornes sont calculées. Pour les limites en plus et moins l'infini, le résultat est directement obtenu en utilisant la croissance comparée. Pour les limites en 0 plus et 0 moins, on analyse les termes de la fonction f et on conclut que ces limites tendent vers plus l'infini. Enfin, le même processus est effectué pour le cas où n est impair. On constate que le tableau de variation est différent et que les limites en 0 plus et 0 moins tendent vers moins l'infini. Ce cours met l'accent sur l'importance de faire une distinction de cas et illustre les différentes étapes de l'étude de fonctions et de limites.

Composition : Déf

Dans cette vidéo, l'auteur explique la composition de deux fonctions. Il commence par donner un exemple concret, en décomposant la fonction racine de x² plus 7 en trois étapes. Ensuite, il donne une définition théorique de la composition de fonctions, en notant VU comme la fonction définie par V2U2x. Il explique ensuite les propriétés de la composition de fonctions, notamment l'associativité et le fait que la composition n'est pas commutative. Il donne un exemple concret pour montrer que V rond U est différent de U rond V dans la plupart des cas. Il conclut en rappelant que la composition de fonctions n'est pas commutative et invite les spectateurs à poser des questions dans le forum.

Dériver une composée

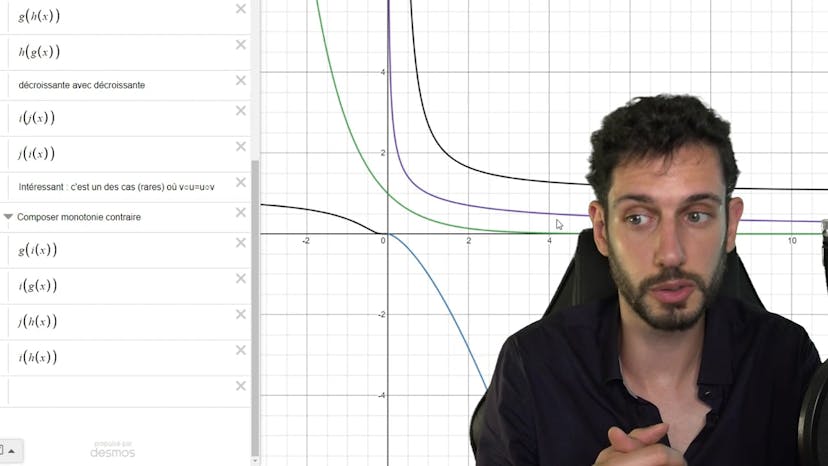
Dans cette vidéo, nous allons voir comment dériver une fonction composée. Avant de commencer, rappelons rapidement ce qu'est la composition. En première, nous avons déjà vu les bases de la composition, mais maintenant nous allons approfondir notre compréhension théorique. La composition nécessite certaines contraintes sur les ensembles d'arrivée et de départ des fonctions que nous composons. Pour dériver une fonction composée, nous allons reprendre des exemples que nous connaissons déjà. Au lieu de nous lancer directement dans une formule théorique, nous préférons commencer par des exemples plus simples. Reprenons l'exemple de la fonction 1/x, nous savons déjà que sa dérivée est -1/x^2. Donc, intuitivement, nous pourrions penser que la dérivée de 1/u est -1/u^2. Cependant, cela n'est pas correct. En réalité, la bonne formule est 1/u' = -u'/u^2. Nous devons toujours prendre en compte le facteur u' dans notre formule. Poursuivons avec l'exemple de la racine de x. Nous savons que la dérivée de la racine de x est 1/(2√x). Une fois de plus, intuitivement, nous pourrions penser que la dérivée de la racine de u est 1/(2√u). Mais nous devons prendre en compte le facteur u'. La bonne formule est u'/(2√u). Nous voyons ici un motif se dessiner : le facteur intuitif que nous connaissons, multiplié par u'. Si nous continuons, nous pouvons rappeler que la dérivée de e^u est e^u * u'. Voici un tableau récapitulatif des différentes dérivées : a*u+b = a*u' + b, u^2 = 2*u*u', u^3 = 3*u^2*u', u^n = n*u^(n-1) * u', 1/u = -1/u^2 * u', etc. Il y a toujours ce facteur u' qui s'ajoute. La formule générale se résume donc à : v o u' = v' o u * u'. Une conséquence intéressante est que si v et u ont la même monotonie (toutes les deux croissantes ou toutes les deux décroissantes), alors la fonction composée v o u est croissante. Par contre, si elles ont des monotonies opposées (une croissante et une décroissante), alors la fonction composée v o u est décroissante. Nous pouvons également voir cela à travers quelques exemples graphiques. J'espère que tout cela est clair, n'hésitez pas à poser des questions sur le forum. Bon entraînement avec les vidéos de méthodes et à la prochaine !

Fonction Composée

Dans cette leçon, nous étudions une fonction composée et apprenons comment effectuer son étude et construire le tableau de variation. L'exemple donné est la fonction E2-1/ x². Nous identifions la fonction h comme étant l'exponentielle, définie et dérivable sur R, tandis que la fonction g est égale à -1/ x², définie et dérivable sur R* (sauf en 0). En composant ces deux fonctions, nous concluons que f est définie sur R*. Nous utilisons ensuite les formules de dérivation pour trouver que g' est égal à 2/ x³ (du même signe que x), et nous pouvons en déduire les variations de g et construire son tableau de variation. Les limites de g sont également calculées dans le tableau complet. Le sens de variation de F est ensuite étudié en analysant la variation de H. En utilisant les règles des sens de variation (croissant avec croissant donne croissant, etc.), nous concluons que F est décroissante sur R* - et croissante sur R* +. Les limites de F sont calculées en utilisant les limites de G et H par composition. Enfin, nous obtenons le tableau de variation complet de F. La fonction n'est pas définie en 0, ce qui ne peut pas être détecté sur une calculatrice. Cependant, dans le contexte de la continuité, nous pourrions étendre la fonction en définissant F(0) = 0. Une autre méthode aurait été d'étudier directement la fonction F en calculant sa dérivée, mais cette approche a été évitée dans cette leçon. Si vous avez des questions, n'hésitez pas à les poser sur la FAQ.

En construction !

Aucun résumé n'est disponible pour cette vidéo

Dérivabilité par la définition formelle

Dans cette vidéo, nous abordons un exercice concernant la notion de prolongement par continuité. On examine une fonction f définie par f(x) = x^2*sin(1/x). On doit prouver trois choses : 1) f peut être prolongée par continuité en 0, 2) f est dérivable sur R, et 3) f' n'est pas continue en 0. Pour montrer que f peut être prolongée par continuité en 0, nous commençons par noter que f est continue sur R* (l'ensemble des réels non nuls) car elle est le produit et la composition de fonctions continues. Ensuite, nous prouvons que f a une limite finie en 0. En effet, en utilisant les bornes du sinus, nous encadrons f(x) par -x^2 et x^2. Or, ces deux expressions tendent vers 0 lorsque x tend vers 0. Donc, par encadrement, on conclut que f(x) tend vers 0 lorsque x tend vers 0. Ainsi, f est prolongeable par continuité en 0. Ensuite, nous montrons que f est dérivable sur R. Comme précédemment, on remarque que f est dérivable sur R* car elle est le produit et la composition de fonctions dérivables. Pour prouver qu'elle est dérivable en 0, nous revenons à la définition fondamentale de la dérivée, qui est la limite du taux d'accroissement. En calculant le taux d'accroissement, nous trouvons que celui-ci est égal à h*sin(h). En utilisant l'encadrement du sinus, nous concluons que h*sin(h) tend vers 0 lorsque h tend vers 0. Donc, f est dérivable sur tout R. Enfin, nous démontrons que f' n'est pas continue en 0. Nous utilisons une caractérisation séquentielle de la limite pour cela. En calculant f', nous obtenons f'(x) = 2x*sin(1/x) - cos(1/x). En choisissant une suite un égale à 1/(2πn), nous remarquons que un tend vers 0 lorsque n tend vers l'infini, mais f'(un) = -1 pour tout n appartenant à N. Ainsi, la limite de f'(un) n'est pas égale à 0, qui est la valeur attendue pour la dérivée en 0. Par conséquent, nous concluons que f' n'est pas continue en 0 et donc que f n'est pas C1 sur R. En résumé, dans cette vidéo, nous avons montré que la fonction f(x) = x^2*sin(1/x) peut être prolongée par continuité en 0, est dérivable sur tout R, mais que sa dérivée f' n'est pas continue en 0, ce qui signifie que f n'est pas C1 sur R.

Inégalités classiques !

Dans cette vidéo, nous avons abordé un exercice classique en mathématiques qui consiste à démontrer trois inégalités importantes. La première inégalité à démontrer est que pour tout x supérieur ou égal à 0, le sinus de x est inférieur ou égal à x. En étudiant les variations de la fonction sinus de x moins x, nous montrons que cette fonction est décroissante et atteint son maximum en 0. Ainsi, nous concluons que pour tout x dans R+, le sinus de x est inférieur ou égal à x. La deuxième inégalité à démontrer est que pour tout x appartenant à R, l'exponentielle de x est supérieure ou égale à 1 plus x. Nous utilisons le fait que la fonction exponentielle est convexe pour montrer que sa courbe se situe au-dessus de sa tangente en 0, qui est x plus 1. Par conséquent, pour tout x dans R, l'exponentielle de x est supérieure ou égale à 1 plus x. Enfin, la dernière inégalité à démontrer est que pour tout x dans (-1, +∞), le logarithme népérien de 1 plus x est inférieur ou égal à x. En utilisant le fait que la fonction ln de 1 plus x est concave, nous montrons que sa courbe se situe en-dessous de sa tangente en 0, qui est x. Ainsi, pour tout x dans (-1, +∞), ln de 1 plus x est inférieur ou égal à x. Ces inégalités sont classiques et importantes à maîtriser, et vous les utiliserez fréquemment en prépa et même dans votre vie.

Fonction réciproque

Dans ce cours, nous étudions une fonction polynomiale de degré 3, f, et nous devons montrer qu'elle possède une fonction réciproque, g, sur R. Ensuite, nous devons montrer que g est dérivable sur R et exposer g' en fonction de g. Enfin, nous devons prouver que g est deux fois dérivable sur R, exposer g'' en fonction de g et donner la valeur de g'' en 0. Tout d'abord, nous notons que f est continue et dérivable sur R puisqu'elle est un polynôme de degré 3. Nous dérivons f et remarquons que sa dérivée est strictement positive, ce qui implique que f est strictement croissante sur R. De plus, f tend vers plus l'infini lorsque x tend vers plus l'infini et f tend vers moins l'infini lorsque x tend vers moins l'infini. En analysant le graphique de f, nous observons qu'elle visite toutes les valeurs de R une seule fois, ce qui est la définition d'une fonction bijective. Par conséquent, f est bijective de R dans R et possède une fonction réciproque, g. Ensuite, nous démontrons que g est dérivable en utilisant un rappel. Si f est dérivable et bijective avec f' strictement supérieur à 0 pour tout x, alors la fonction réciproque g est dérivable sur l'image du domaine de définition de f et g' est égal à 1 sur f'g. Dans notre cas, nous avons déjà prouvé que f est dérivable sur R avec f' strictement supérieur à 0. Donc, g' de y est égal à 1 sur 3g²y plus 1, où y est dans R. Pour la question suivante, nous utilisons les résultats précédents. Nous dérivons g' à l'aide de la formule obtenue précédemment et nous obtenons une expression pour g'. Ensuite, nous remplaçons g' par cette expression pour obtenir une réponse cohérente avec les questions précédentes. Finalement, nous trouvons g' de 0, qui est égal à -1 sur 36.

Fonction C1

Dans cet exercice, nous avons deux fonctions, f(x) et g(x), et nous devons déterminer si elles sont dérivables ou continûment dérivables. Pour la fonction f(x), nous avons montré qu'elle est continue et dérivable sur R* (l'ensemble des réels non nuls). Ensuite, nous avons prouvé que f(x) est dérivable en 0 en utilisant la définition du nombre dérivé. Nous avons conclu que le taux d'accroissement de f tend vers 0 lorsque h tend vers 0, ce qui signifie que f est dérivable en 0 et que f'(0) = 0. Ensuite, nous avons examiné si f'(x) est continue en 0. Nous avons remarqué que pour tout x dans R*, f'(x) = 2x sin(1/x) - cos(1/x). En utilisant le rappel que f(x) tend vers l lorsque x tend vers a si et seulement si pour toute suite un tendant vers a, f(un) tend vers l, nous avons posé un = 1/(2πn) pour tout n dans N. Nous avons montré que un tend vers 0 lorsque n tend vers l'infini et que f'(un) = -1 pour tout n dans N, ce qui est différent de 0. Par conséquent, nous avons conclu que f est dérivable sur R mais pas continue, ce qui signifie qu'elle n'est pas C1 (continûment dérivable) sur R. Pour la fonction g(x), nous avons montré de la même manière que précédemment qu'elle est C1 sur R* et dérivable en 0. Ensuite, nous avons montré que g'(x) est continue en 0 en calculant sa dérivée g'(x) = 3x² sin(1/x) - x cos(1/x). En utilisant l'inégalité triangulaire et le fait que sin(1/x) et cos(1/x) sont inférieurs ou égaux à 1, nous avons montré que g'(x) tend vers 0 lorsque x tend vers 0, ce qui est égal à g'(0). Par conséquent, nous avons conclu que g est C1 sur R. Résumé SEO friendly: Dans cet exercice, nous avons analysé les fonctions f(x) et g(x) pour déterminer leur dérivabilité et leur continuité. Nous avons montré que f(x) est dérivable en 0 mais pas continue sur R, tandis que g(x) est dérivable en 0 et continue sur R.

Dérivée d’une composée

Dans cette transcription de la vidéo, Corentin présente un exercice qui combine la dérivation et les polynômes. L'exercice consiste à montrer que la dérivée de la fonction f(x) est égale à une autre fonction Q(x), où f(x) est défini comme f(x) = P(1/(1-x)) * e^(1/(1-x)). On doit également trouver la relation entre les polynômes P(x) et Q(x). Pour résoudre cet exercice, Corentin propose de dériver. La dérivée de f(x) est alors égale à P'(1/(1-x)) * (1-x)^2 * e^(1/(1-x)) + P(1/(1-x)) * (1/(1-x))^2 * e^(1/(1-x)). En factorisant par e^(1/(1-x)), on obtient le polynôme Q(1/(1-x)) = P'(1/(1-x)) + P(1/(1-x)) * (1/(1-x))^2. En posant Q(x) = P'(x) + P(x) * x^2, on obtient notre polynôme Q(x) et la relation entre Q et P. Cet exercice est simple, mais il est souvent demandé lors des examens oraux et écrits car il est fréquemment utilisé.

Dérivée n-ième

Bonjour à tous, c'est Corentin. Aujourd'hui, nous avons un exercice qui demande beaucoup de calculs et de concentration. L'énoncé demande de dériver la fonction f(x) = x^2 * ln(1+x) n fois. Nous remarquons qu'il s'agit du produit de deux fonctions, ce qui nous amène à la formule de Leibniz. Selon cette formule, la dérivée n-ième de f est égale à la somme des produits de g dérivée k fois et de h dérivée n-k fois, pour k allant de 0 à n. En identifiant nos fonctions g(x) = ln(1+x) et h(x) = x^2, nous pouvons trouver les dérivées successives. Après quelques calculs, nous obtenons que g'(x) = 1+x, g''(x) = -1/(1+x)^2, et pour tout k supérieur ou égal à 3, g^(k)(x) = 0. Quant à h(x), nous avons h'(x) = 2x et h''(x) = 2. Maintenant, nous pouvons appliquer la formule de Leibniz en réinjectant les dérivées trouvées. La fonction f dérivée n fois est égale à une expression compliquée, mais nous pouvons la simplifier en factorisant par v(x). Nous travaillons alors avec v(x) qui est égal à 2x^2 + 2nx + n(n-1). En développant et simplifiant v(x), nous trouvons que f^(n)(x) = 2x^2 + 2nx + n^2 - n(x/(1+x)^2). Finalement, nous arrivons à une expression plus simple pour la dérivée n-ième de f(x) qui est 2x^2 + 2nx + n^2 - n(x/(1+x)^2). Cet exercice nécessite des calculs précis et de la rigueur. Cependant, il est important de noter qu'il est essentiel de simplifier les expressions et de diviser le travail en étapes. La compréhension de la formule de Leibniz, l'identification des fonctions et le domaine de définition, ainsi que la capacité à simplifier sont des compétences clés pour résoudre cet exercice.