 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Corrigés de BAC
Bac Maths
Terminale

Géométrie - Nouvelle Calédonie 2022
L'exercice porte sur la géométrie dans l'espace et aborde plusieurs concepts classiques. Dans un premier temps, on nous demande de trouver les coordonnées du point G, qui est obtenu en additionnant les vecteurs AB, AD et AE. En utilisant les relations données, on obtient les coordonnées de G qui sont (3, 2, 1). Ensuite, on nous demande de montrer que le vecteur N de coordonnées (2, 0, -3) est un vecteur normal au plan EHI, et de déterminer une équation cartésienne de ce plan. En utilisant la formule d'une équation cartésienne et en remplaçant les coordonnées d'un point sur le plan, on trouve que l'équation cartésienne de EHI est 2X - 3Z + 3 = 0. Ensuite, on nous demande de trouver les coordonnées du point I en utilisant les informations sur le triangle EIF et le plan EHI. En remplaçant les coordonnées de I dans l'équation cartésienne de EHI, on trouve que ZI = 2. Les coordonnées de I sont donc (3.5, 0, 2). On nous demande ensuite de déterminer une mesure au degré près de l'angle EIF en utilisant le produit scalaire. En calculant le produit scalaire entre les vecteurs IE et IF et en utilisant la formule du cosinus, on trouve que l'angle EIF mesure environ 112.6 degrés. Enfin, on nous demande de donner une représentation paramétrique de la droite delta passant par le point R(6, -3, -1) et dirigée par le vecteur U(-3, 4, 1). La représentation paramétrique de delta est alors x = 6 - 3t, y = -3 + 4t, z = -1 + t. On nous dit également qu'une équation du plan BFG est x = 3. Finalement, on nous demande de déterminer les coordonnées du point K, intersection de la droite delta et du plan BFG. En remplaçant x par 3 dans la représentation paramétrique de delta, on obtient une équation en une inconnue t. En résolvant cette équation, on trouve que t = 1, et en remplaçant t par 1 dans les coordonnées de delta, on trouve que les coordonnées de K sont (3, 1, 0). On nous demande également de vérifier si le point K appartient au segment BC, et en observant que les coordonnées de K sont les demi-sommes des coordonnées de B et C, on conclut que K est bien le milieu de BC et donc qu'il appartient au segment BC.
Corrigés de BAC
Bac Maths
Terminale

Suites et fonctions - Centres étrangers 2022
Dans cet exercice de BAC, nous devons étudier les exponentielles et les suites. Nous commençons par trouver les limites de la fonction h(x) = e^x - x. On détermine les limites lorsque x tend vers plus ou moins l'infini. En utilisant la méthode de factorisation, nous trouvons que la limite de h en plus l'infini est plus l'infini et la limite de h en moins l'infini est plus l'infini. Ensuite, nous analysons les variations de h en utilisant sa dérivée. Nous trouvons que h est décroissante pour x négatif et croissante pour x positif. Nous dressons un tableau de variations en utilisant les limites trouvées précédemment.
Ensuite, nous étudions la fonction f(x) = e^x et trouvons son équation de tangente au point d'abscisse 0. En utilisant la dérivée de f, nous trouvons que la tangente a pour équation y = x + 1.
Ensuite, nous introduisons la suite un = e^(1/n) - 1/n - 1 et déterminons sa limite lorsque n tend vers plus l'infini. En utilisant les propriétés des limites, nous trouvons que la limite de un est 0.
Enfin, nous démontrons que pour tout entier naturel non nul n, un+1 - un = h(1/(n+1)) - h(1/n). En utilisant les résultats précédents sur les variations de h, nous trouvons que la suite un est décroissante.
En utilisant un tableau de valeurs, nous trouvons la plus petite valeur de n pour laquelle l'écart entre la tangente et la courbe de f est inférieur à 0,01. En lisant dans le tableau, nous trouvons que n = 8 est la valeur recherchée.
Corrigés de BAC
Bac Maths
Terminale

Probabilités - Centres étrangers 2022
Dans cet exercice, nous abordons les notions de probabilités et de variables aléatoires. Nous sommes dans le contexte de la fabrication de paires de lunettes et nous avons deux traitements possibles, T1 et T2. Nous devons calculer différentes probabilités, notamment en utilisant les probabilités conditionnelles et la loi binomiale.
Nous commençons par remplir un tableau en utilisant les probabilités données dans l'énoncé. Ensuite, nous calculons la probabilité qu'une paire de verres présente un défaut pour au moins un des deux traitements. Pour cela, nous utilisons la formule de l'union des événements.
Ensuite, nous calculons la probabilité qu'une paire de verres présente un défaut pour les deux traitements. Pour cela, nous utilisons la formule de l'intersection des événements.
Nous vérifions ensuite si les événements A et B sont indépendants en utilisant la formule des probabilités conditionnelles.
Nous calculons ensuite la probabilité qu'une paire de verres présente un défaut pour un seul des deux traitements, en utilisant la formule de l'union des événements moins la probabilité de l'intersection.
Nous calculons également la probabilité qu'une paire de verres présente un défaut pour le traitement T2, sachant qu'elle présente un défaut pour le traitement T1 en utilisant la formule des probabilités conditionnelles.
Ensuite, nous passons à la partie B de l'exercice, où nous considérons un échantillon de 50 paires de verres prélevées au hasard dans la production. Nous introduisons la variable aléatoire X, qui compte le nombre de paires de verres présentant le défaut pour le traitement T1 dans cet échantillon.
Nous montrons que X suit une loi binomiale de paramètres n = 50 et p = 0,1.
En utilisant la formule de la probabilité d'une loi binomiale, nous calculons la probabilité d'avoir exactement 10 paires de verres présentant ce défaut dans l'échantillon.
Nous calculons également l'espérance de la variable aléatoire X, qui donne en moyenne le nombre de paires de verres dans un échantillon de 50 avec ce défaut.
Cela conclut l'exercice sur les probabilités.
Corrigés de BAC
Bac Maths
Terminale

Géométrie - Centres étrangers 2022
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Maths
Terminale

Suites et fonctions 1 - Centres étrangers-2 2022
Dans cet exercice de BAC sur les fonctions et suites, on nous pose différentes questions. Dans la première question, on nous donne une fonction g et on nous demande de déterminer sa convexité. Pour cela, on dérive deux fois la fonction et on observe le signe de la dérivée seconde. En analysant les résultats, on conclut que la fonction g est convexe.
Dans la deuxième question, on nous demande de déterminer si une tangente est parallèle à une droite donnée. Pour cela, on regarde le coefficient directeur de la tangente, qui est égal à la dérivée de la fonction au point considéré. En observant les graphiques, on conclut que la tangente est parallèle à la droite d'équation y = x.
Dans la troisième question, on nous demande si une suite est majorée, bornée ou minorée. On observe que la suite est comprise entre -1 et 1, ce qui signifie qu'elle est bornée.
Dans la quatrième question, on nous indique que la suite change de signe à chaque terme. En analysant cette propriété, on conclut que les termes de la suite ont le même signe si leur indice est pair, et un signe différent si leur indice est impair.
Dans la cinquième question, on nous donne des valeurs pour une suite et on nous demande de déterminer une autre valeur manquante. En utilisant les équations données, on trouve rapidement la valeur recherchée.
Dans la sixième question, on nous dit qu'une suite est définie par une formule complexe et on nous demande quelles sont ses variations. En analysant la formule, on conclut que la suite est décroissante.
Enfin, dans la dernière question, on nous donne des informations sur le temps de génération des cellules. En utilisant des calculs mathématiques, on détermine qu'il faut environ 20 minutes pour qu'une cellule se divise en deux.
Cet exercice aborde différents aspects des fonctions et suites, en utilisant des calculs et des raisonnements logiques pour parvenir aux réponses.
Corrigés de BAC
Bac Maths
Terminale

Suites et fonctions 2 - Centres étrangers-2 2022
Aucun résumé n'est disponible pour cette vidéo
Corrigés de BAC
Bac Maths
Terminale

Probabilités - Centres étrangers-2 2022
Dans cet exercice de bac sur les probabilités, nous devons effectuer différents calculs avec des probabilités conditionnelles et des variables aléatoires. Pour commencer, nous avons des informations sur une étude statistique réalisée dans une entreprise, qui indiquent que 48% des salariés sont des femmes et 52% sont des hommes. Parmi les femmes, 16,5% sont cadres et parmi les hommes, 21,5% sont cadres.
Ensuite, nous devons représenter cette situation par un arbre pondéré, en prenant en compte les différentes probabilités. Par exemple, la probabilité d'être une femme est de 0,48 et la probabilité d'être un cadre sachant que c'est une femme est de 0,165. Nous utilisons ces informations pour calculer la probabilité que la personne choisie soit une femme qui exerce une profession de cadre, soit 0,0792.
Nous devons ensuite démontrer que la probabilité que la personne choisie exerce une profession de cadre est égale à 0,191, en utilisant la formule des probabilités totales. La probabilité d'être un cadre sachant que c'est un homme est également calculée.
Par la suite, nous devons déterminer si les événements "être une femme" et "être un cadre" sont indépendants en comparant la probabilité de leur intersection avec le produit de leurs probabilités respectives. Dans ce cas, les événements ne sont pas indépendants.
Nous introduisons ensuite une variable aléatoire X qui représente le nombre de cadres parmi un échantillon de 15 salariés. Nous déterminons la probabilité que l'échantillon contienne zéro ou un cadre, soit 0,1890.
Nous calculons ensuite l'espérance de la variable aléatoire X en utilisant la formule correspondante.
Dans la dernière partie de l'exercice, nous considérons un échantillon de N salariés et cherchons la valeur minimum de N pour avoir une probabilité supérieure ou égale à 0,99 d'avoir au moins un cadre dans cet échantillon. En utilisant le logarithme, nous trouvons que N doit être supérieur ou égal à 22.
Cet exercice met en pratique différentes notions de probabilités, notamment les probabilités conditionnelles, les probabilités totales et les variables aléatoires.
Maths Expertes
Arithmétique
Terminale

Division euclidienne
Dans cette transcription vidéo, Paul nous explique la division euclidienne de -534 par 6. Il précise que bien que parfois appelée division euclidienne, l'écriture correcte pour celle-ci est "moins 534 égale à 6 fois Q plus R". Il rappelle également que le dividende est -534, le diviseur est 6, le quotient (Q) peut être positif ou négatif, et le reste (R) doit être compris entre 0 et 6 exclus.
Paul procède ensuite à la division. En prenant -53 comme base, il explique qu'il faut multiplier par -8 pour atteindre -534. Le reste est alors -5, et en ajoutant le 4, il descend à -54. Il explique ensuite que pour atteindre 0, on multiplie par -9. Ainsi, le quotient est -89 et le reste est 0.
En conclusion, la division euclidienne de -534 par 6 est -534 égale à -89 fois 6 plus 0. Paul recommande d'écrire "+0" pour montrer que l'on a bien compris l'écriture de la division euclidienne. Il termine en disant au revoir et en donnant rendez-vous pour la prochaine fois.
Maths Expertes
Arithmétique
Terminale

CAPITAL : Reste de 145²⁰²² par 7 ?
Dans cet exercice de congruence, on nous demande de trouver le reste dans la division par 7 de 145 puissance 2022. Pour résoudre cet exercice, il est important de comprendre et connaître une méthode spécifique.
Tout d'abord, on simplifie le nombre 145 en le réduisant modulo 7, ce qui donne un reste de 5. On utilise ensuite une technique pour comprendre le comportement des différentes puissances de 5. On remarque un cycle dans les restes des puissances successives, où le reste peut être 3, 4, 2, 3, etc.
On utilise alors une règle des congruences qui dit que si A est congruent à B, alors A puissance N est congruent à B puissance N. On applique cette règle pour réduire la puissance 2022 à la puissance 2022 modulo 6, car 5 est plus simple que 145.
En étudiant les différentes puissances de 5 modulo 6, on remarque qu'au bout de 6 puissances, on a un cycle qui se répète. On montre alors qu'on a couvert tous les entiers naturels, car tout entier peut s'écrire comme un multiple de 6, un multiple de 6 plus 1, etc.
Maintenant, on se concentre sur la puissance 2022. On remarque que 2022 est pair et divisible par 3 (la somme de ses chiffres est 6), donc il est dans la case correspondant à un multiple de 6.
Finalement, on conclut que 145 puissance 2022 est congru à 5 puissance 2022, qui est congru à 1.
Il est important de comprendre cette méthode en profondeur et de savoir l'utiliser, car elle est très utile pour résoudre de nombreux exercices de congruence et d'arithmétique.
Maths Expertes
Arithmétique
Terminale

Divisibilité et fraction
Dans cette vidéo, nous abordons un exercice de mathématiques qui concerne la fraction 35 sur n-4. Nous devons déterminer pour quelles valeurs de l'entier n (différentes de 4), cette fraction sera entière.
Il est important de prendre en compte que n est un entier relatif et non un entier positif ou naturel. Beaucoup d'élèves se trompent à ce niveau et perdent des points.
Pour résoudre cet exercice, nous devons étudier les diviseurs de 35. Les diviseurs de 35 sont 1, 5, 7, et 35. Ils sont également présents dans leur version négative : -1, -5, -7, et -35.
Maintenant, nous devons vérifier si n-4 appartient à l'ensemble des diviseurs de 35. Donc nous devons résoudre les équations :
- n-4 = 1, ce qui donne n = 5
- n-4 = 5, ce qui donne n = 9
- n-4 = 7, ce qui donne n = 11
Remarquons qu'il ne faut pas inclure 4 dans les réponses car n doit être différent de 4.
Finalement, les solutions entières sont les nombres 5, 9, et 11.
J'espère que cette vidéo vous a été utile. A bientôt pour une prochaine vidéo.
Maths Expertes
Arithmétique
Terminale

Divisibilité de n⁵-n ?
Le cours porte sur la factorisation de l'expression a_n = n^5 - n. L'auteur recommande de procéder à une étape de simplification initiale en factorisant l'expression, ce qui permet d'avoir une version plus simple pour les calculs ultérieurs.
Ensuite, l'auteur se concentre sur la démonstration que a_n est un nombre pair. Plutôt que de faire une table de congruence, l'auteur remarque que le produit de deux entiers consécutifs (n-1 et n) est toujours pair, car l'un des deux est toujours pair. Par conséquent, a_n est divisible par 2.
Pour la question suivante, qui est de montrer que a_n est divisible par 3, l'auteur utilise le fait que n-1, n et n+1 sont trois entiers consécutifs, et donc l'un des trois est toujours un multiple de 3. Par conséquent, leur produit, a_n, est divisible par 3.
Enfin, l'auteur utilise les congruences modulo 5 pour montrer que a_n est divisible par 5. En analysant les différentes valeurs possibles pour n modulo 5, l'auteur constate que le produit n*(n-1)*(n+1)*(n^2+1) est toujours congru à 0 modulo 5. Par conséquent, a_n est divisible par 5.
En conclusion, l'auteur souligne l'importance d'investir dans une simplification préalable de l'expression, ce qui permet de faciliter les démonstrations ultérieures. L'auteur utilise également les propriétés des entiers consécutifs et des congruences modulo pour simplifier les calculs et parvenir rapidement aux résultats.
Maths Expertes
Arithmétique
Terminale
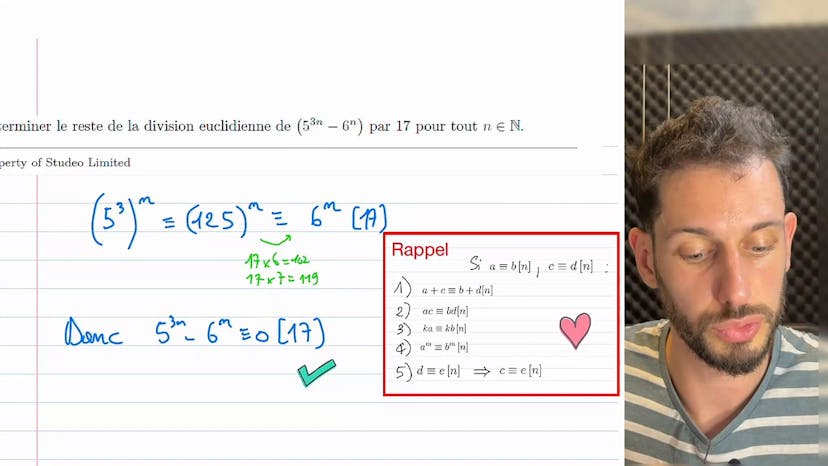
Reste de 5³ⁿ - 6ⁿ par 17 ?
Bonjour à tous, dans cet exercice sur les congruences, nous abordons un exemple de calcul de la division Euclidienne qui peut sembler complexe au premier abord. Il s'agit de trouver le reste de la division de 5 puissance 3n moins 6 puissance n par 17.
Plutôt que de nous précipiter dans une table de congruence, nous prenons le temps de réfléchir à une approche plus simple. Nous pouvons examiner séparément les congruences de 5 puissance 3 et 6 puissance n modulo 17 pour essayer de déceler un schéma ou un cycle.
Nous commençons par simplifier l'expression 5 puissance 3n en utilisant la propriété des puissances : 5 puissance 3n = (5 puissance 3) puissance n = 125 puissance n. Ensuite, nous utilisons la propriété de congruence pour simplifier modulo 17 en enlevant les multiples de 17.
Par exemple, nous pouvons enlever 102 (puisque 17x3 = 51 et 51x2 = 102) et même un peu plus en enlevant 119 (102 + 17) car cela reste éloigné de 125.
Ainsi, nous obtenons 125 congru à 6. En conclusion, 5 puissance 3n moins 6 puissance n est toujours congru à 0 modulo 17. Cela signifie que 17 divise toujours cette expression.
J'espère que cette explication vous aura été utile. Je vous donne rendez-vous pour de nouvelles vidéos.


