 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Probabilités
Terminale

Déterminer le + petit entier
Le cours porte sur la détermination du plus petit entier k tel que la probabilité que la variable aléatoire X, qui suit une loi binomiale de paramètres n=50 et p=0,63, soit inférieur ou égal à k est supérieure ou égale à 0,5.
La méthode utilisée consiste à calculer les probabilités que X soit inférieur ou égal à différents nombres de manière décroissante à l'aide d'une calculatrice.
En partant de 40 et en diminuant progressivement, on remarque que la probabilité que X soit inférieur ou égal à 36 est égale à 0,93, ce qui est inférieur à la probabilité souhaitée de 0,95.
Ainsi, on conclut que le plus petit entier k recherché est égal à 37.
Maths Spé
Probabilités
Terminale

Somme de VA : Bernoulli
Dans cet exercice, nous avons 300 variables aléatoires indépendantes suivant une loi de Bernoulli de paramètre p égal à 0,23. La question est de déterminer la loi de la variable aléatoire x, qui est la somme de ces 300 variables aléatoires.
Pour comprendre cela, nous faisons deux rappels. D'abord, un schéma de Bernoulli est la répétition de n épreuves de Bernoulli identiques et indépendantes. Ensuite, nous rappelons qu'une loi binomiale de paramètre np donne le nombre de succès sur n répétitions.
Dans notre cas, x est la somme des 300 variables aléatoires indépendantes suivant une loi de Bernoulli de paramètre p égal à 0,23. En sommant ces variables, nous comptons le nombre de succès sur les 300 répétitions. Donc, x suit une loi binomiale de paramètre n égal à 300 et p égal à 0,23.
De plus, nous rappelons que l'espérance d'une variable aléatoire suivant une loi binomiale est égale à n fois p. Dans notre cas, n est égal à 300 et p est égal à 0,23, donc l'espérance de x est égale à 69.
Maths Spé
Probabilités
Terminale

Somme de VA de même loi
Dans cette vidéo, nous abordons un exercice de probabilité portant sur la somme de variables aléatoires indépendantes. Plus précisément, l'exercice consiste à tourner une roue de loterie comportant cinq secteurs angulaires égaux plusieurs fois. Chaque secteur a une valeur de points attribuée, soit 300 points pour les deux premiers secteurs, 100 points pour le troisième secteur et moins 400 points pour les deux derniers secteurs.
Nous devons décomposer la variable aléatoire Z, représentant le gain algébrique en points à la fin du jeu, en une somme de variables aléatoires identiques et indépendantes. Ensuite, il nous est demandé de calculer l'espérance de Z, c'est-à-dire la moyenne des gains.
En procédant à cette décomposition, nous identifions que Z est égal à x1 + x2 + x3 + x4, où x1 représente le gain algébrique au premier lancé de roue. Nous déduisons également que les x1 suivent une certaine loi : x1 est égal à 300 avec une probabilité de 0,4, à 100 avec une probabilité de 0,2 et à moins 400 avec une probabilité de 0,4.
Pour calculer l'espérance de Z, nous pouvons utiliser la propriété d'additivité de l'espérance. Ainsi, nous obtenons l'espérance de Z en additionnant l'espérance de chaque x1, x2, x3 et x4. Comme les variables aléatoires suivent la même loi, nous multiplions l'espérance de x1 par 4.
En substituant les valeurs correspondantes, nous trouvons que l'espérance de Z est égale à 4 fois moins 20, ce qui donne moins 80. En d'autres termes, en moyenne, les joueurs perdront 80 euros ou 80 points en jouant à ce jeu.
Maths Spé
Probabilités
Terminale

Modéliser par une somme (1)
Dans cette vidéo, Corentin présente un exercice portant sur les variables aléatoires et la modélisation probabiliste d'événements. L'exercice consiste à lancer un dé tétraédrique équilibré dont les faces sont numérotées de 1 à 4, ainsi qu'un dé cubique équilibré dont les faces sont numérotées de 1 à 6. L'objectif est d'étudier la somme des résultats des deux dés (D2D) et de proposer deux variables aléatoires x et y qui permettent de modéliser la situation.
Corentin suggère de réfléchir à cette situation de manière logique, en pensant comme un programme informatique. Il explique que x représente le résultat obtenu avec le dé tétraédrique et y représente le résultat obtenu avec le dé cubique. Ainsi, la somme x + y représente la somme des résultats des deux dés.
Il propose ensuite un bonus, qui est de calculer l'espérance de x + y. L'espérance de x + y est égale à l'espérance de x + l'espérance de y. En considérant que les résultats des deux dés sont équiprobables, Corentin effectue les calculs nécessaires et trouve que l'espérance est égale à 6. Il interprète alors cela comme signifiant qu'en moyenne, le participant à ce jeu obtient un score de 6.
En résumé, l'exercice consiste à modéliser la somme des résultats de deux dés en utilisant les variables aléatoires x et y, et à calculer l'espérance de cette somme, qui s'avère être égale à 6.
Maths Spé
Probabilités
Terminale

Modéliser par une somme (2)
Dans cette vidéo, nous étudions la notion de somme de variables aléatoires en utilisant un exercice pratique. Elia s'entraîne au jet de 7 mètres et fait 30 tirs le matin et 50 l'après-midi. Elle a une probabilité de marquer de 0,46 le matin et de 0,78 l'après-midi. Les tirs sont supposés indépendants.
Nous devons tout d'abord déterminer la loi suivie par la variable aléatoire x, qui représente le nombre de tirs réussis par Elia le matin, et la loi suivie par y, qui représente le nombre de tirs réussis par Elia l'après-midi.
En analysant la situation, nous remarquons que cela correspond à une expérience de Bernoulli, où réussir le tir est considéré comme un succès et rater le tir comme un échec. Nous devons donc comptabiliser le nombre de succès, c'est-à-dire le nombre de fois qu'Elia réussit son tir.
Étant donné l'indépendance des tirs, nous concluons que x suit une loi binomiale avec les paramètres 30 et 0,46, où 30 représente le nombre de tirs et 0,46 la probabilité de réussir le tir le matin. De la même manière, y suit une loi binomiale avec les paramètres 50 et 0,78, où 50 représente le nombre de tirs et 0,78 la probabilité de réussir le tir l'après-midi.
Ensuite, nous devons comprendre ce que représente la somme des variables aléatoires x et y, c'est-à-dire x + y. Il s'agit du nombre total de tirs réussis pendant la journée.
Enfin, nous devons calculer l'espérance de x + y. Nous savons que l'espérance d'une variable aléatoire binomiale est égale à n fois p, où n est le nombre de tirs et p est la probabilité de réussir le tir. Nous calculons donc l'espérance de x, qui est égale à 30 fois 0,46, et l'espérance de y, qui est égale à 50 fois 0,78. En fin de compte, nous trouvons que l'espérance de x + y est égale à 45. Cela signifie qu'Elia peut espérer réussir 45 tirs au cours de la journée.
Maths Spé
Probabilités
Terminale

Utiliser l'Inégalité de B-T
Dans cette vidéo, Corentin aborde la première méthode consacrée aux inégalités et concentrations en terminale. Il commence par lire l'énoncé qui concerne une variable aléatoire, donnant le débit de la Loire en mètre cube par seconde à un instant t. Une étude statistique a permis de déterminer que l'espérance de la variable est de 350 et que la variance est de 28000.
Dans un premier temps, il est demandé de donner une majoration de la probabilité que le débit de la Loire soit écarté de plus ou moins 200 mètres cubes par seconde de son cours moyen et d'interpréter cette majoration. Corentin utilise ensuite l'inégalité de Bien-Aimé Tchibitchev, qui établit une relation entre l'espérance et la variance d'une variable aléatoire, pour majorer cette probabilité à 0,7. Cela signifie que la probabilité que le débit de la Loire soit écarté de plus ou moins 200 mètres cubes par seconde de son cours moyen est inférieure ou égale à 0,7.
Dans un second temps, il est demandé de donner une minoration de la probabilité que le débit de la Loire soit strictement compris entre 50 et 650 mètres cubes par seconde. Corentin utilise à nouveau l'inégalité de Bien-Aimé Tchibitchev pour se ramener à cette question. Il pose l'expression 1 moins la probabilité que la valeur absolue de la différence entre le débit de la Loire et son espérance soit supérieure ou égale à 300. En utilisant l'inégalité de Tchibitchev, il trouve que cette probabilité est égale à 0,311. Par conséquent, la probabilité que le débit de la Loire soit compris entre 50 et 650 mètres cubes par seconde est supérieure ou égale à 0,311.
Maths Spé
Probabilités
Terminale

Inegalité de concentration
Dans cette vidéo, Corentin nous présente une méthode pour résoudre un problème lié aux variables aléatoires et aux inégalités. Le problème consiste à trouver une estimation de la probabilité que la valeur absolue de la variable aléatoire moyenne soit supérieure ou égale à 3, étant donné un échantillon de variables aléatoires binomiales.
Corentin commence par expliquer qu'il souhaite redémontrer l'inégalité de concentration en utilisant l'inégalité de Bienaimé-Chebyshev. Il vérifie d'abord si l'espérance de la variable aléatoire moyenne est égale à 9, ce qui est nécessaire pour appliquer l'inégalité de Chebyshev. En effectuant les calculs, il constate que l'espérance est bien de 9.
Ensuite, il utilise l'inégalité de Bienaimé-Chebyshev pour dire que la probabilité que la valeur absolue de la variable aléatoire moyenne moins 9 soit supérieure ou égale à 3 est inférieure ou égale à la variance de la variable divisée par 9. Il reste donc à calculer la variance de la variable aléatoire moyenne.
Corentin rappelle que la variance de la variable aléatoire moyenne est égale à la variance de chaque variable divisée par le nombre de variables. En effectuant les calculs, il obtient une variance de 0,0225.
Enfin, en divisant cette quantité par 9, il conclut que la probabilité recherchée est inférieure ou égale à 0,0025.
Corentin insiste sur le fait que l'inégalité de concentration est utile pour résoudre ce problème, en utilisant l'inégalité de Bienaimé-Chebyshev pour démontrer le résultat.
Maths Spé
Probabilités
Terminale

Utiliser la LGN
Dans ce cours, nous discutons des inégalités et des concentrations que vous rencontrerez en terminale. Plus précisément, nous examinons un exercice dans lequel nous devons estimer l'espérance de la variable aléatoire XI.
L'énoncé nous dit que nous devons remplir un questionnaire qui comprend le nombre d'enfants de moins de 18 ans dans le foyer. On appelle X1 à X1000 les variables aléatoires qui représentent les réponses des mille premiers utilisateurs. Nous faisons l'hypothèse que ces variables aléatoires sont indépendantes et identiquement distribuées.
Pour estimer l'espérance de XI, nous utilisons le graphique qui montre l'évolution de la moyenne du nombre d'enfants de moins de 18 ans par utilisateur. Nous rappelons alors la loi des grands nombres, qui dit que lorsque nous avons un échantillon de variables aléatoires X1 à XN avec une espérance attendue mu, la moyenne empirique Mn de cet échantillon tend vers l'espérance mu lorsque la taille de l'échantillon tend vers l'infini.
Dans notre cas, nous remarquons que la moyenne empirique Mn tend vers 1,5 lorsque la taille de l'échantillon devient très grande. Par conséquent, nous estimons que l'espérance de XI est égale à 1,5.
Il est important de noter que la moyenne empirique tend vers l'espérance en probabilité, et non exactement. Cependant, cela peut être étudié plus en détail dans le cadre des études en mathématiques.
En résumé, dans cet exercice, nous utilisons la loi des grands nombres pour estimer l'espérance de la variable aléatoire XI, en se basant sur les réponses des utilisateurs à un questionnaire sur le nombre d'enfants de moins de 18 ans dans le foyer. Nous constatons que la moyenne empirique tend vers 1,5 lorsque la taille de l'échantillon augmente, ce qui nous permet d'estimer que l'espérance de XI est également de 1,5.
Maths Spé
Probabilités
Terminale

Concentration et taille d'échantillon
Dans cette vidéo, Corentin aborde un exercice sur l'inégalité de concentration. D'abord, il explique qu'une urne contient deux jetons marqués "3", deux jetons marqués "5" et un jeton marqué "10". En tirant un jeton de l'urne, on obtient une variable aléatoire X qui représente le nombre obtenu. Corentin détermine ensuite l'espérance de X, qui est égale à 5,2, et la variance de X, qui est égale à 6,56.
Ensuite, Corentin aborde la question de savoir combien de tirages avec remise peuvent être effectués pour être sûr à 95% que la moyenne des nombres obtenus se situe entre 5 et 5,4. Pour cela, il utilise l'inégalité de concentration. Il vérifie d'abord les hypothèses nécessaires pour appliquer cette inégalité, à savoir que les tirages sont avec remise et que les variables aléatoires sont un échantillon de variances 6,56.
Corentin définit alors la variable aléatoire moyenne M de cet échantillon et cherche à trouver la valeur de n telle que la probabilité que M-5,2 soit supérieure ou égale à 0,2 soit inférieure ou égale à 0,05. Il utilise l'inégalité de concentration pour trouver une condition suffisante pour cela, à savoir que 164/n soit inférieure ou égale à 0,05. En résolvant cette inégalité, Corentin conclut que si n est supérieur ou égal à 3280, on est sûr à 95% que la moyenne obtenue sera comprise entre 5 et 5,4.
Maths Spé
Probabilités
Terminale

Echantillon et prélèvement INSEE
Dans cette vidéo, Corentin nous parle de l'importance des échantillons et de la façon de les définir et de les manipuler. Il commence par nous présenter une lecture détaillée sur les achats en ligne en France en 2018, où 75,4% des personnes interrogées âgées de 15 à 29 ans ont réalisé un achat sur Internet au cours des 12 derniers mois. Ensuite, il explique comment il a réalisé une enquête en interrogeant 500 personnes de cette même population pour savoir si elles ont réalisé un achat en ligne au cours des 12 derniers mois.
Il souligne que, étant donné la taille de la population française, il suppose que les tirages au sort successifs n'affectent pas les probabilités de réponse positive ou négative, et donc que le prélèvement de 500 personnes peut être assimilé à un tirage avec remise. Il crée une liste de variables aléatoires, X1 à X500, où Xi est égal à 1 si la personne Y a réalisé un achat en ligne au cours des 12 derniers mois, et 0 sinon.
Il répond ensuite à deux questions. Dans la première question, il explique que la liste X1 à X500 peut être considérée comme un échantillon de variables aléatoires indépendantes, suivant toutes une loi de Bernoulli avec un paramètre de 0,754. Cela est dû au fait que les tirages au sort successifs n'affectent pas les probabilités des réponses.
Dans la deuxième question, il utilise deux méthodes pour calculer l'espérance et la variance de la somme S, qui est la somme des variables Xi de 1 à 500. La première méthode consiste à dire que S est la somme de variables aléatoires indépendantes et de même loi, ce qui donne une espérance de 377 et une variance de 92,742. La deuxième méthode consiste à considérer que S suit une loi binomiale de paramètres n=500 et p=0,754, ce qui donne également une espérance de 377 et une variance de 92,742.
En conclusion, Corentin nous rappelle l'importance des échantillons et nous remercie pour notre attention.
Maths
Algèbre
MPSI/PCSI

Est-ce un EV ? Avec un SEV
Le cours concerne les espaces vectoriels et présente des techniques pour montrer si un espace est un espace vectoriel ou non. Il y a deux techniques principales :
1) Montrer que l'espace est un sous-espace vectoriel d'un espace vectoriel connu en vérifiant trois propriétés : l'inclusion dans un espace vectoriel, la conservation des éléments par combinaison linéaire et la présence de zéro dans l'espace.
2) Montrer que l'ensemble peut être écrit comme un VECT (ensemble des combinaisons linéaires) puisque tous les VECTS sont des espaces vectoriels.
Il est également possible d'utiliser la notion de noyau d'une application linéaire pour montrer qu'un espace est un espace vectoriel.
Le cours présente plus en détail la technique 1 pour un exemple spécifique où l'ensemble E1 est l'ensemble des vecteurs de R3 dont les coordonnées vérifient une équation donnée. Les trois critères sont vérifiés pour montrer que E1 est un sous-espace vectoriel de R3.
Maths
Algèbre
MPSI/PCSI
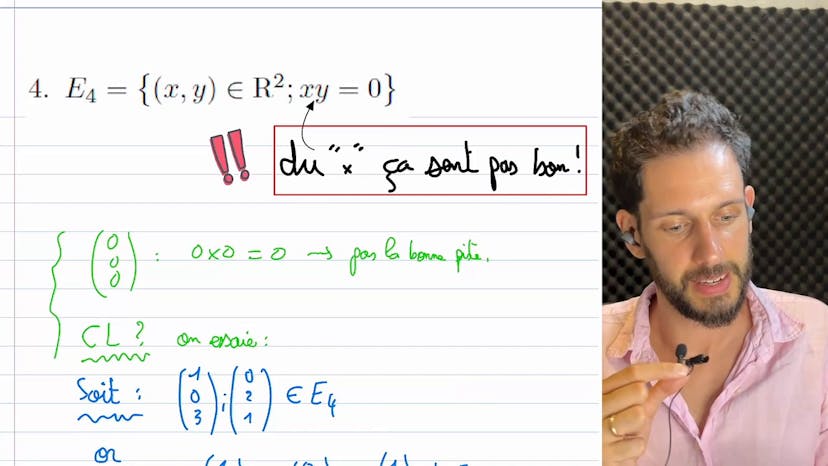
Cas où ce n'est PAS un EV
Dans cet extrait, le cours fait référence à différents cas où l'espace n'est pas un espace vectoriel. Le premier cas étudié est celui de E2, où l'équation x + y + 3z = 2 est donnée. Il est souligné que cette équation a une constante séparée des variables, ce qui indique un caractère non linéaire. En utilisant les définitions de base d'un espace vectoriel, il est prouvé que E2 n'est pas un espace vectoriel car l'élément 0 n'appartient pas à l'espace.
Les cas 4 et 5 sont également présentés comme des exemples où l'espace n'est pas un espace vectoriel. Il est mentionné que la technique habituelle de montrer que 0 n'appartient pas à l'espace ne fonctionne pas pour ces cas. Au lieu de cela, il est suggéré de trouver deux éléments dans l'espace tels que le produit de leurs coordonnées soit égal à 0. Ensuite, il est spécifié que si E4 est un espace vectoriel, la somme de ces deux éléments devrait également être dans E4. En prenant l'exemple de 1, 0 et 0, 2, il est montré que leur somme, 1, 2, n'est pas dans E4, ce qui prouve que E4 n'est pas un espace vectoriel.
Le dernier exemple présenté s'appelle E5 et montre également une relation non linéaire. Il est souligné que dès qu'il y a des constantes ou des relations non linéaires, cela peut indiquer que l'espace n'est pas un espace vectoriel. En prenant l'exemple de Y = X^2, il est prouvé que E5 n'est pas un espace vectoriel en montrant que la somme de deux éléments dans E5 n'est pas dans E5.
En résumé, le cours discute de ces différents cas pour illustrer des situations où l'espace n'est pas un espace vectoriel en utilisant des outils tels que l'élément 0 n'appartenant pas à l'espace, l'absence de conservation par combinaison linéaire, et l'existence de relations non linéaires ou de constantes.


