Online Complexes course by Top Instructors - Complexes

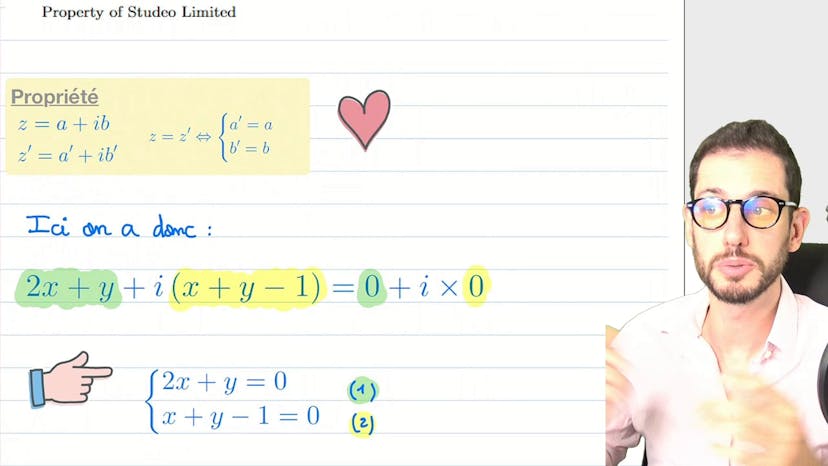
Partie réelle et imaginaire

Un nombre complexe est composé d'une partie réelle et d'une partie imaginaire, et s'écrit généralement sous la forme Z = A + iB. Pour résoudre une équation avec des nombres complexes, on peut utiliser une méthode classique en identifiant les deux complexes. Les complexes ont deux dimensions, la partie réelle et la partie imaginaire. L'équation donne 2X + Y comme partie réelle et X + Y - 1 comme partie imaginaire. On peut écrire cette équation sous forme de système en mettant les deux parties égales à 0. Après avoir résolu le système, on trouve X = -1 et Y = 2. Cette méthode permet d'identifier les solutions d'une équation complexe.

Rappel : le conjugué

Le cours traite du concept de conjugué d'un nombre complexe. Le conjugué de z = a + ib est noté z-bar et égal à a - ib. Le cours explique les propriétés du conjugué, à savoir que le conjugué de la somme de deux nombres complexes est égal à la somme des conjugués, que le conjugué du produit de deux nombres complexes est égal au produit des conjugués, et enfin que le conjugué du quotient de deux nombres complexes est égal au quotient des conjugués. Ensuite, le cours présente une équation à résoudre pour z, en utilisant le concept de conjugué. Pour cela, il introduit a et b tel que z = a + ib, et à partir de là, il effectue des calculs pour identifier les parties réelles et imaginaires de l'équation, ce qui permet de résoudre pour a et b et de trouver la solution. Le cours conclut en soulignant qu'il existe d'autres astuces plus avancées pour résoudre ces équations, mais la méthode basique de l'introduction de a et b reste valide et simple à utiliser. Le cours invite les étudiants à poser des questions et se termine en annonçant la prochaine vidéo.

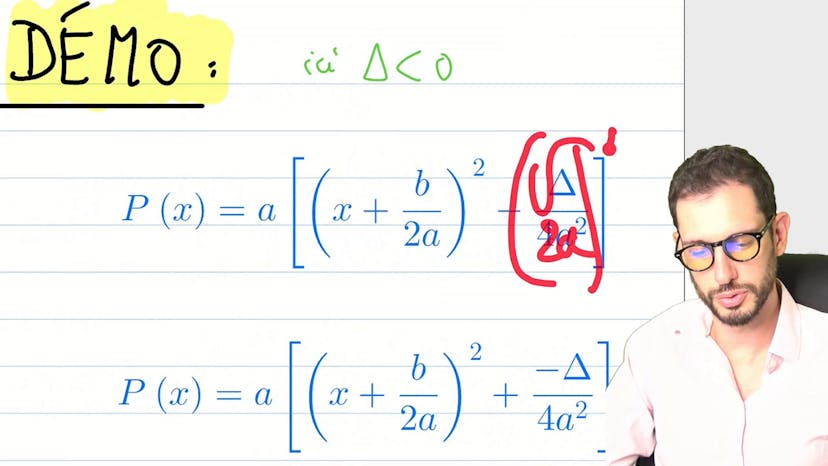
Second degré Δ<0

Dans ce cours, nous étudions les polynômes du second degré dans les nombres réels. Si le discriminant Δ est positif, cela signifie qu'il existe deux solutions réelles distinctes. Si Δ est nul, il existe une seule solution réelle qui touche la courbe de la parabole. Si Δ est négatif, cela signifie qu'il n'y a pas de solution réelle. Cependant, si nous élargissons notre domaine aux nombres complexes, même lorsque Δ est négatif, il existe des racines imaginaires conjuguées. Nous utilisons une formule pour factoriser les polynômes du second degré, où nous introduisons le discriminant Δ. Selon le signe de Δ, nous pouvons ou non factoriser le polynôme. Lorsque Δ est positif, nous pouvons utiliser une identité remarquable pour factoriser le polynôme. Lorsque Δ est négatif, nous sommes dans le domaine des complexes, où nous utilisons une propriété importante: a² + b² = (a + bi)(a - bi). En appliquant cette formule, nous obtenons les solutions complexes du polynôme. À titre d'exemple, nous calculons Δ pour un polynôme donné et trouvons les solutions complexes correspondantes. En conclusion, nous soulignons l'importance de la propriété des complexes et nous sommes disponibles pour répondre à toute question supplémentaire.

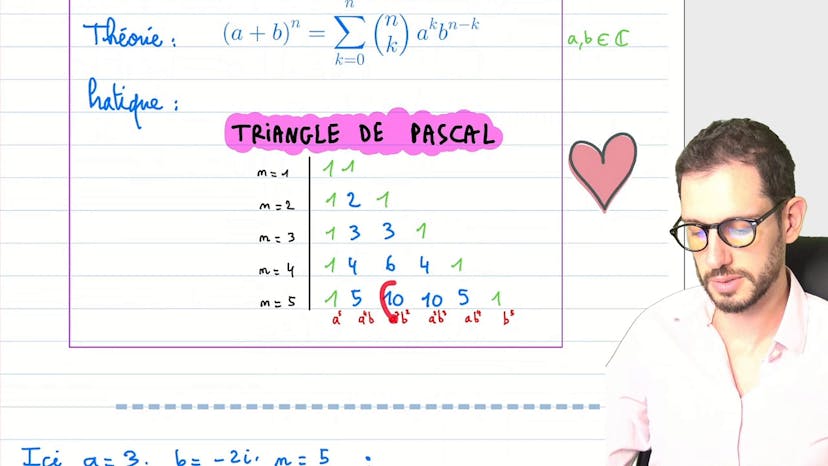
Binôme de Newton

Le cours parle de la formule du binôme de Newton, qui permet de calculer la puissance d'une somme de deux nombres (A + B)^N. Il explique que cette formule peut être utilisée pour tout nombre complexe A et B. Pour rappel, la formule est la suivante : A^N + (N parmi 1) * A^(N-1) * B + (N parmi 2) * A^(N-2) * B^2 + ... + B^N. Le professeur explique que la formule peut sembler compliquée, mais qu'en pratique, on peut la gérer de manière plus simple en suivant deux aspects. Le premier aspect est de se rendre compte qu'il y a N+1 termes dans la formule, du terme 1 au terme N, ainsi que le terme 0. Chaque terme correspond à une combinaison de puissances de A et B dont la somme est toujours égale à N. Par exemple, pour N=6, on aurait les termes A^6, A^5 * B, A^4 * B^2, A^3 * B^3, A^2 * B^4, A * B^5, B^6. Le deuxième aspect est la nature de chaque terme. Chacun d'entre eux est un produit de A et B avec des puissances cohérentes, et leur quantité peut être calculée à l'aide de factoriels ou du triangle de Pascal. Le triangle de Pascal permet de trouver les coefficients des différents termes pour chaque valeur de N, en suivant les règles suivantes : il y a toujours un 1 au début et à la fin de chaque ligne, et chaque coefficient est la somme des deux coefficients au-dessus de lui dans le triangle. Le professeur donne des exemples concrets pour illustrer l'utilisation de la formule, et explique que le but est de pouvoir comprendre et appliquer la logique du triangle de Pascal et du binôme de Newton, plutôt que de mémoriser la formule brute. Enfin, il donne un exemple spécifique en utilisant la formule pour calculer la puissance de (3-2i)^5, en rappelant une propriété intéressante sur les puissances successives de i. Il invite les étudiants à faire le calcul eux-mêmes et à poser des questions s'ils en ont besoin.

Quantité conjuguée

Dans ce cours, nous apprenons une méthode classique pour trouver la forme algébrique de certains nombres complexes. L'objectif est de se débarrasser des racines au dénominateur en multipliant par la quantité conjuguée. Par exemple, nous pouvons multiplier par racine de 5 moins 1 pour obtenir une quantité sans racine. Cette méthode s'applique également aux nombres complexes. Nous faisons ensuite un exemple détaillé pour illustrer cette méthode. Nous utilisons ensuite cette méthode pour résoudre une équation. Il est important de se rappeler que peu importe ce qui se trouve dans le numérateur, seule la méthode de multiplication dépend du dénominateur. Il est crucial d'être sûr de sa méthode et de ne pas se laisser perturber par des facteurs externes. L'objectif est de garder la tête froide et d'avancer avec la méthode apprise. En utilisant la méthode de multiplication par la quantité conjuguée, nous résolvons l'équation donnée pour trouver la valeur de z. En résumé, ce cours présente une méthode fondamentale pour exprimer les nombres complexes sous forme algébrique. Il est important de la connaitre par cœur afin de l'appliquer efficacement lorsque cela est nécessaire.

Z est-il réel ? V1

Ce cours aborde une méthode classique en mathématiques qui est souvent utilisée dans des exercices plus complexes. La méthode consiste à trouver l'ensemble de valeurs d'un complexe "z" pour lesquelles une quantité donnée, appelée "grand z", est réelle. On utilise la méthode de la quantité conjuguée pour simplifier l'expression et obtenir une conclusion. Dans cet exercice, on nous donne un petit z qui n'est pas égal à moins 1 et on nous demande de trouver les valeurs de ce petit z pour lesquelles grand z est réel. En utilisant la méthode de la quantité conjuguée, on développe l'expression et sépare les termes réels. On simplifie ensuite l'expression et on trouve que b doit être nul pour que le petit z soit réel. La solution finale est donc l'ensemble des nombres réels à l'exception de moins 1.

Z est-il réel ? V2

Le cours présente une méthode pour déterminer si un nombre complexe est réel en utilisant la propriété du conjugué. Le conjugué d'un nombre complexe est obtenu en changeant le signe de sa partie imaginaire. Si un nombre complexe est égal à son conjugué, alors il est réel. Cette méthode est élégante mais pas toujours optimale, car certains cas nécessitent l'utilisation des coefficients A et B. Le cours explique comment appliquer la propriété du conjugué dans différentes opérations mathématiques, telles que la soustraction et la multiplication, pour simplifier les expressions. En appliquant ces propriétés, on arrive à la conclusion que si un nombre complexe est égal à son conjugué, alors il est réel. Cette méthode est présentée comme une astuce supplémentaire à connaître, mais il est recommandé de comprendre le concept du conjugué pour l'utiliser correctement.

Equation bicarré complexe

Dans cette vidéo, le cours aborde le concept d'équation bicarrée, qui est une équation de degré 4 sans termes en x3 ou x. Pour résoudre ce type d'équation, il est possible d'effectuer un changement de variable pour se ramener à une équation de degré 2 plus facile à gérer. L'équation bicarrée étudiée dans cet exemple est z^4 + 3z^2 - 10 = 0. En posant z^2 = Z, l'équation devient Z^2 + 3Z - 10 = 0, une équation de degré 2. Pour résoudre cette nouvelle équation, plusieurs méthodes sont possibles. Dans cet exemple, l'auteur suggère de tester les racines évidentes, et dans ce cas, 2 est une racine. En utilisant le fait que 10 est le produit des deux racines, l'autre racine est -5. Ainsi, le polynôme a deux racines réelles, Z = 2 et Z = -5. Ensuite, en résolvant pour z, puisque z^2 = Z, on obtient z = √2 et z = -√2, qui sont les solutions réelles. Cependant, l'une des racines de l'équation initiale étant négative, cela implique l'introduction de nombres complexes. Ainsi, les solutions de l'équation bicarrée sont √2, -√2, i√5 et -i√5. En conclusion, pour résoudre une équation bicarrée, il est nécessaire d'effectuer un changement de variable et de gérer les racines de manière logique. Les solutions peuvent être réelles ou complexes, en fonction des conditions de l'équation. Cet apprentissage permet de comprendre comment résoudre les équations bicarrées et est idéal pour ceux qui souhaitent approfondir leurs connaissances en mathématiques.

Factoriser un cube ?!

Dans cette vidéo, l'exercice consiste à factoriser une expression complexe. Le professeur explique que même si cela peut sembler difficile au premier abord, il existe une astuce pour résoudre cet exercice plus rapidement. Il remarque que les nombres 27 et 8 peuvent être exprimés sous forme cubique (3 au cube et 2 au cube respectivement). De plus, il fait remarquer que i au cube est égal à -i. Grâce à ces observations, il peut réécrire l'expression initiale comme suit: 27z3-8i=3z³+2i³. En utilisant une formule connue qui dit que x³+y³ est égal à (x+y)(x²-xy+y²), il factorise l'expression pour obtenir: 27z3-8i=(3z+2i)(9z²-6zi+4i²). Le professeur souligne que cette méthode est plus avancée, mais qu'il est important de connaître cette formule et d'être capable d'observer ces astuces pour résoudre rapidement des exercices de ce type.

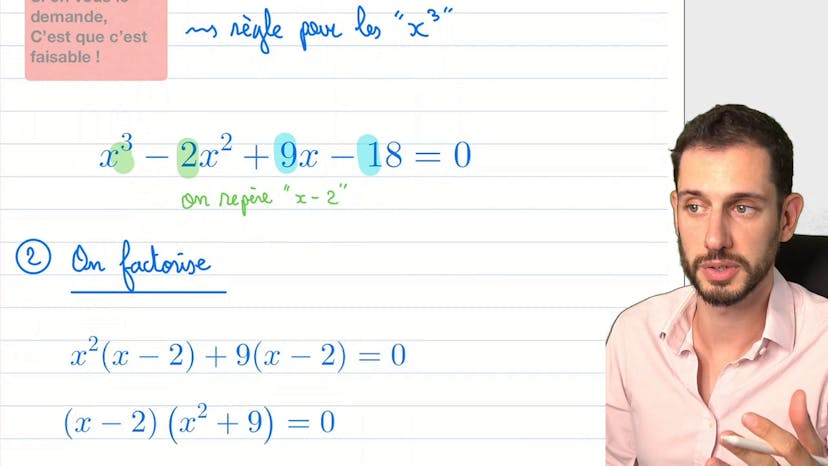
Factoriser un cube pire !!

Ce cours aborde la résolution d'un exercice de mathématiques. L'instructeur souligne l'importance de bien connaître le cours et de ne pas paniquer face à des exercices plus difficiles. Il explique qu'en observant attentivement l'énoncé, on peut trouver des indices pour résoudre l'exercice. Dans cet exemple, il remarque la présence de termes similaires et en déduit une factorisation. Ensuite, il résout l'équation et trouve les solutions correctes. Il corrige une petite erreur dans sa conclusion et donne une explication sur l'intérêt d'observer attentivement les exercices plus difficiles. Il invite les étudiants à poser des questions ou à demander des précisions dans les commentaires.

Inégalité triangulaire, partie réelle et imaginaire d’un quotient

Dans ce cours, Paul aborde plusieurs questions sur les complexes. Pour la première question, il utilise l'inégalité triangulaire pour établir une inégalité. Pour la deuxième question, il explique comment exprimer la partie réelle et la partie imaginaire de A sur B en fonction des parties réelles et imaginaires de A et B, ainsi que du module de B. Paul suggère d'utiliser les formules qui lient partie réelle, partie imaginaire, module, et le nombre et son conjugué. Ensuite, il calcule les parties réelles et imaginaires de 1+Eialpha et 1+Eibêta. Il fait également référence à la formule de l'air pour simplifier les calculs. Il note que cette formule est très utile dans les problèmes complexes et encourage à la retenir. En conclusion, Paul résume les résultats obtenus et donne quelques conseils pour mieux visualiser les angles complexes. Il termine en soulignant l'importance de comprendre les formules de l'air.

Équations polynomiales

Dans cette vidéo, Paul explique comment résoudre des équations du second degré à coefficient complexe. La technique pour résoudre ces équations est similaire à celle des équations en réel. Les solutions de l'équation AZ² + BZ + C = 0 sont Z1 = (-B - √Δ)/2A et Z2 = (-B + √Δ)/2A, où Δ = B² - 4AC. Paul résout une première équation avec A = 1, B = 1 et C = 1, et obtient les solutions Z1 = 1 + i et Z2 = 1 + 2i. Ensuite, Paul aborde une deuxième équation déguisée en équation du second degré en utilisant la substitution X = Z3. Il résout l'équation du second degré en X et trouve Δ = -15 - 8i. Pour trouver la racine carrée de Δ, il pose Δ = a + ib et utilise l'équation Δ² = Δ, ce qui donne les équations sur la partie réelle et la partie imaginaire de Δ. En résolvant ces équations, il obtient A = 1 et B = -4, ou A = -1 et B = 4. Les solutions de cette deuxième équation sont x1 = 1 - i et x2 = 3i. Cependant, Paul souhaite maintenant trouver les solutions pour l'équation originale. Il résout l'équation E1 en écrivant Z3 = 1 - i ou Z3 = 3i, sous forme exponentielle. Il utilise la racine 1ère de l'unité pour résoudre cette équation et obtient six solutions au total. Il conclut en disant que cela est cohérent avec le fait que le polynôme de départ était de degré 6. Ce résumé explique comment résoudre des équations du second degré à coefficient complexe et décrit les étapes suivies par Paul pour résoudre deux exemples spécifiques.