Online Calcul algébrique et trigonométrie course by Top Instructors - Calcul algébrique et trigonométrie

Inéquations trigonométriques

Dans cette vidéo, Mathilde Studio explique comment résoudre des inéquations trigonométriques compliquées. Pour résoudre la première inéquation, elle recommande de représenter le cercle trigonométrique et de limiter les valeurs de cos(x) à une plage spécifique. Pour la seconde inéquation, elle utilise une formule de cosinus pour se ramener à une équation plus gérable. Pour la troisième inéquation, elle ajoute des racines pour utiliser une formule trigonométrique et la résoudre. Enfin, pour la quatrième inéquation, elle utilise une transformation pour isoler cos(x/3) et l'expresser en fonction de cos(pi/4) et sin(x/3) en utilisant une formule trigonométrique. Elle explique comment extraire les solutions sur l'intervalle 0 à 2pi pour obtenir les solutions finales. Elle fournit également des astuces pratiques pour résoudre les inéquations trigonométriques en général.

Formule de duplication

Dans cette vidéo, Mathis de studio explique comment calculer les cosinus et sinus de π sur 8 de manière exacte sans utiliser de calculatrice. Il démontre que π sur 8 peut être ramené à des angles plus connus comme π sur 3, π sur 6 et π sur 4. A partir de là, il utilise la formule classique de cosinus 2x pour trouver la valeur exacte de cosinus 2π sur 8, qui est approximativement égal à 0.92. Il utilise la même logique pour trouver la valeur exacte de sinus 2π sur 8, qui est approximativement égal à 0.38. La démarche est intéressante car elle montre comment trouver des valeurs exactes en utilisant des formules connues.

Formule d'addition

Cette vidéo de Matisse de Studio explique comment calculer les sinus et les cosinus de pi sur 12 de manière exacte. Il explique que même si ce ne sont pas des angles courants, on peut les ramener à des angles de référence tels que pi sur 6, pi sur 3 et pi sur 4. Il donne deux méthodes pour calculer ces angles : diviser pi sur 12 par 2 ou le représenter comme pi sur 3 moins pi sur 4. En utilisant les formules trigonométriques de base, il calcule ensuite le cosinus de pi sur 12 (1 + racine de 3 sur 2 racine de 2) et le sinus de pi sur 12 (racine de 3 moins 1 sur 2 racine de 2). Il conclut en encourageant les gens à utiliser ces méthodes pour ramener les angles rares à des angles connus et à manipuler les formules de la trigonométrie de base.

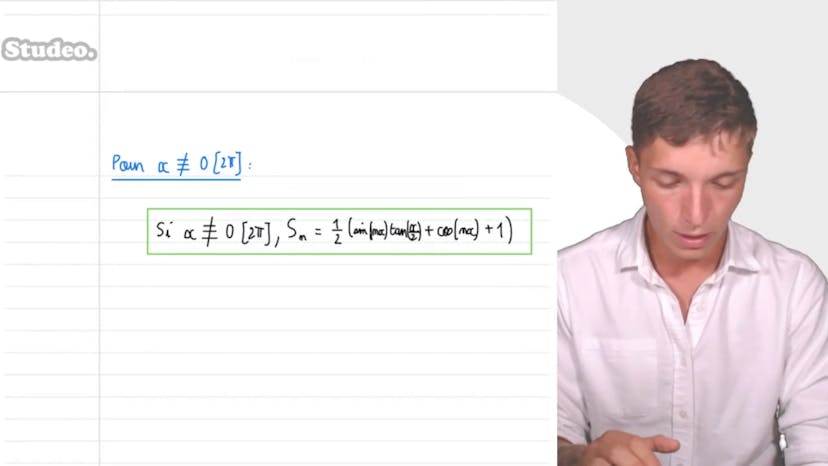
Sommes trigonométriques

Dans cette vidéo, Mathis de Studio explique comment calculer des sommes de cosinus et sinusoïdes. Il commence par expliquer comment calculer la somme pour k allant de 0 à n de cosinus kx, où n est un nombre entier négatif et x est un réel. Il utilise la formule de trigonométrie 2 sin a cos b pour simplifier l'expression. Il en vient alors à la somme télescopique, qui est une somme où la fonction évaluée en n+1 moins la fonction évaluée en 0 donne la somme recherchée. Il applique cette technique pour trouver la somme pour k allant de 0 à n de sinus kx. Ensuite, il utilise cette technique pour trouver la somme pour k allant de 0 à n de cosinus carré kx et la somme pour k allant de 0 à n de sinus carré kx. Enfin, il résume les résultats obtenus pour ces différentes sommes et explique l'importance de la digestion de cas lorsqu'on divise des fonctions trigonométriques.

Autour de la tangente

Dans cette vidéo, Mathijs de studio compare deux approches mathématiques : algébrique et trigonométrique pour résoudre une équation complexe. En utilisant des formules, il calcule la tangente de 3θ en fonction de la tangente de θ. Ensuite, il résout l'équation en utilisant une méthode algébrique qui factorise le polynôme et une méthode trigonométrique qui identifie les racines en utilisant la tangente. Il explique également que la tangente est une fonction bijective de -π/2 à π/2 et que chaque élément a un antécédent sur cette plage. Enfin, il conclut que les deux approches donnent le même ensemble de solutions, mais la méthode trigonométrique est plus élégante.

Valeurs remarquables

Dans cette vidéo, Mathis de Studio explique comment résoudre 14 équations trigonométriques en utilisant le cercle trigonométrique, qui est une image importante à connaître en mathématiques et en physique. Il recommande de dessiner le cercle trigonométrique et de se souvenir que pour trouver les solutions, il faut tourner d'un angle de pi à chaque fois. Il résout les équations pour le sinus, le cosinus et la tangente, et donne les ensembles des solutions sur R et sur 0 à pi pour chacune d'entre elles. Il explique également l'astuce pour trouver la tangente et donne des exemples de valeurs plus particulières pour les trigonométriques. Mathis souligne l'importance de connaître le cercle trigonométrique pour résoudre les équations rapidement et sans erreur.

Équations trigonométriques

Dans cette vidéo, Mathis résout des équations trigonométriques en R et dans des intervalles spécifiques. Pour la première équation sin2x = 1/2 sur 0 à Pi, il utilise l'équivalence de la formule du sinus pour résoudre l'inégalité. Pour la deuxième équation tangente de 5x = 1, il divise le résultat par 5 pour trouver la solution de x. Pour la troisième équation la valeur absolue de cosNx = 1, il divise le résultat par N pour obtenir x. Pour la quatrième équation sinus 2x + sinus x = 0, il utilise la formule trigonométrique pour factoriser par sinus x et trouver la solution. Enfin, pour la dernière équation 12cos²x - 8sin²x = 2, il utilise la formule trigonométrique pour se ramener à des égalités plus simples. Mathis explique également qu'il ne faut pas avoir peur des arguments inhabituels des équations et qu'il faut utiliser les formules pour résoudre les équations avec des sinus et des cosinus mélangés. L'ensemble des solutions pour chaque équation est donné pour R et pour l'intervalle donné.

Mathématiques