 All subjects
All subjects
 All subjects
All subjects
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Introduction
Ce cours est une introduction au nouveau sous-chapitre sur les intégrales, les applications et calculs. Le premier point abordé est l'utilisation des méthodes d'intégration pour calculer des primitives plus complexes, telles que l'intégration par parties. Ensuite, il est possible de calculer des aires entre des courbes en utilisant le lien établi entre les aires et les primitives dans le sous-chapitre précédent. De plus, la définition de la valeur moyenne d'une fonction est présentée, avec différentes méthodes associées. En résumé, ce cours aborde le calcul des aires sous une courbe, entre deux courbes, la valeur moyenne d'une fonction, ainsi que les méthodes d'intégration par parties. La partie la plus intéressante est l'accumulation d'exercices et de méthodes plus difficiles pour explorer les limites des calculs d'intégration par parties et d'aires. Bon courage pour cette partie et n'hésitez pas à consulter la FAQ en cas de questions ou de doutes. À bientôt pour la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Intégration par Parties
Dans cette vidéo, nous abordons le thème de l'intégration par parties en mathématiques. L'intégration par parties est une formule qui permet de calculer des intégrales plus complexes.
La formule de l'intégration par parties est la suivante : l'intégrale de uv' est égale à la primitive de uv moins l'intégrale de u'v.
L'intégration par parties est ut
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Aire entre 2 courbes
Dans cette vidéo, nous allons explorer comment calculer l'aire entre deux courbes. Le théorème affirme que si f et g sont deux fonctions continues sur un intervalle i, et que f(x) est toujours plus petite que g(x), alors l'aire entre les courbes de f et g sur cet intervalle est donnée par l'intégrale de g(x) moins f(x) entre les bornes a et b.
Pour illustrer cette propriété, on nous montre deux fonctions f et g. Lorsque f est au-dessus de g, l'aire entre les courbes est calculée sur l'intervalle [a,b], où a serait approximativement 0,2 et b serait environ 3,8, le point d'intersection des courbes. On peut appliquer le théorème précédent pour calculer cette aire, qui vaut l'intégrale de f(x) moins g(x) sur cet intervalle.
Après le point d'intersection, il y a un changement de comportement et c'est g qui devient au-dessus. Donc, l'aire entre les courbes à ce stade est égale à l'intégrale de g(x) moins f(x) entre ce point et 5.
Cette démonstration visuelle est ajoutée pour mieux comprendre la propriété. Si vous avez des questions, consultez la FAQ. À bientôt dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Valeur Moyenne
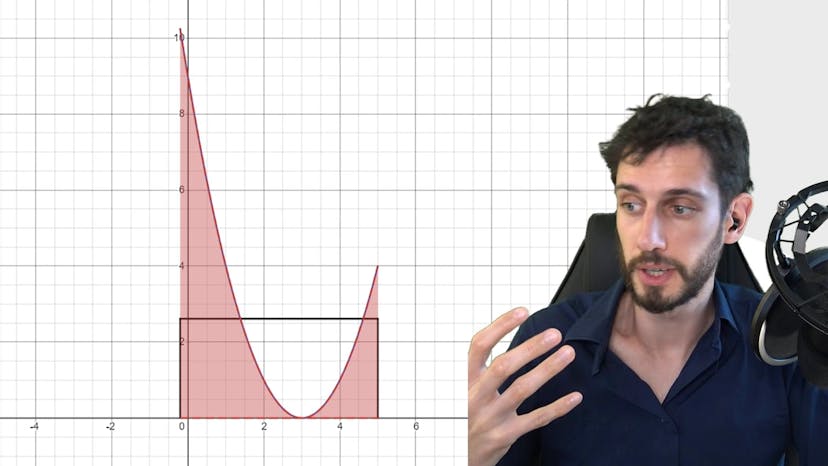
La valeur moyenne d'une fonction f est définie comme étant le nombre µ égal à 1/(b-a) fois l'intégrale de f sur l'intervalle [a,b]. On peut la voir comme une moyenne arithmétique où la somme des valeurs de f est divisée par le nombre total de valeurs. Une autre façon de la visualiser est géométrique : µ est la valeur constante telle que l'aire sous la courbe de la fonction constante égale à µ est égale à l'aire sous la courbe de f. Pour trouver la valeur moyenne, il faut trouver le rectangle où les deux aires sont égales. C'est à ce moment-là que l'on obtient la valeur moyenne.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Intégration par Parties : Calcul
La méthode d'intégration par partie est une méthode utilisée en mathématiques pour calculer certaines intégrales. Elle repose sur une formule spécifique : l'intégrale de U'V est égale à UV moins l'intégrale de UV'. Cette formule découle de la dérivée du produit.
Pour appliquer cette méthode, il faut choisir judicieusement les fonctions U et V'. Les critères sont les suivants : il doit y avoir un produit dans l'intégrale, au moins l'un des deux facteurs doit avoir une primitive facilement calculable et l'autre fonction doit faciliter la dérivation.
Prenons l'exemple de l'intégrale de X ln de X entre 1 et E. On peut choisir U = X et V' = ln de X. La primitive de U est X²/2 et la dérivée de V est 1/X. En utilisant la formule d'intégration par partie, on simplifie l'intégrale initiale en une autre intégrale plus simple à calculer. Finalement, on évalue cette intégrale et obtient le résultat E² + 1/4.
Il est important de noter que l'ordre des fonctions peut parfois être inversé, mais il est préférable de choisir la combinaison qui facilite le calcul. Il est également recommandé d'écrire clairement les fonctions U', U, V et V' pour éviter les erreurs.
En résumé, la méthode d'intégration par partie permet de calculer des intégrales en échangeant une intégrale contre une autre. Le choix des fonctions U et V' est crucial pour simplifier le calcul.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Aire sous une Courbe : Calcul
Nous allons maintenant aborder le calcul des erreurs sous une courbe à l'aide des intégrales. Nous allons prendre deux exemples et calculer les erreurs sous les courbes, ce qui revient à calculer des intégrales.
Le premier exemple concerne l'erreur entre la courbe CF, dont l'équation est f2x = x²-4, et l'axe d'étape 6 entre les droites d'équation x = -2 et x = 2. Mathématiquement, cela correspond à l'intégrale de x²-4dx entre -2 et 2.
Nous cherchons alors la primitive de la fonction à l'intérieur de l'intégrale. La primitive de x²-4 est (1/3)x^3-4x. En utilisant le théorème fondamental, nous savons que l'erreur est égale à (1/3)x^3-4x évaluée entre -2 et 2. Après calculs, nous obtenons une erreur de -32/3.
Pour le deuxième exemple, l'erreur b est calculée entre la courbe et l'axe des abscisses entre les droites d'équation x = -5 et x = 1. Nous effectuons l'intégrale de x²-4dx entre -5 et 1, ce qui donne la même primitive. Après simplification, nous trouvons une erreur de 18.
Il est important de noter que la variable d'intégration est x, et que dans ces cas précis, elle ne peut pas être ailleurs. Il est crucial de faire attention à cela.
En conclusion, nous avons calculé les erreurs grâce aux primitives et nous avons obtenu une erreur négative de -32/3 dans le premier exemple et une erreur de 18 dans le deuxième exemple. Si vous avez d'autres questions, n'hésitez pas à consulter notre FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
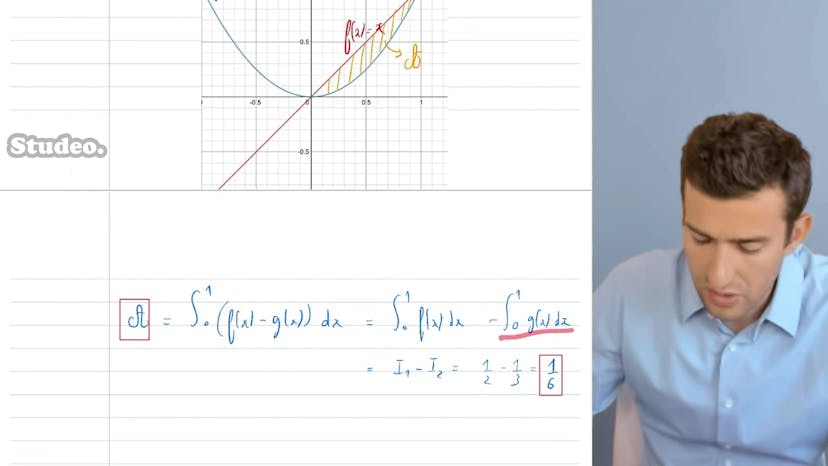
Aire entre 2 Courbes
Dans ce cours, nous apprenons comment calculer l'R entre deux courbes, f(x) = x et g(x) = x², sur l'intervalle de x = 0 à x = 1.
Pour calculer l'R, nous devons d'abord trouver les primitives des deux fonctions f et g. La primitive de f(x) = x est F(x) = x²/2, et la primitive de g(x) = x² est G(x) = x³/3.
En utilisant le théorème fondamental du calcul, l'R se situe entre les courbes f et g, et peut être calculée en trouvant la différence entre les intégrales de f(x) et g(x) sur l'intervalle de x = 0 à x = 1.
Dans ce cas, la fonction f(x) est toujours supérieure à la fonction g(x) sur l'intervalle de 0 à 1. Donc, nous calculons l'intégrale de f(x) - g(x), ce qui équivaut à l'intégrale de 0 à 1 de f(x) moins l'intégrale de 0 à 1 de g(x).
En utilisant les primitives que nous avons trouvées, nous évaluons les intégrales et obtenons les valeurs I1 et I2. I1 est égal à 1/2 et I2 est égal à 1/3. Donc, la différence entre I1 et I2 est égale à 1/2 - 1/3, ce qui donne 1/6.
Ainsi, l'R entre les courbes f(x) et g(x) sur l'intervalle de 0 à 1 est égale à 1/6. C'est ainsi que l'on calcule l'R entre deux courbes.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Calcul Valeur Moyenne
Le cours explique comment calculer la valeur moyenne d'une fonction à partir de deux exemples : la fonction f et la fonction g, avec des intervalles différents. La valeur moyenne est définie comme l'intégrale de la fonction sur l'intervalle divisée par la largeur de l'intervalle. Pour trouver cette valeur moyenne, on doit trouver une primitive de la fonction intégrale. Dans le premier exemple, on pose h égale à x² plus 3, et on utilise le théorème fondamental pour trouver que la valeur moyenne est de 13 tiers. Dans le deuxième exemple, on veut la valeur moyenne de g, qui est x sur x²-3. On remarque que c'est un quotient et on l'écrit comme u' sur u. On trouve que la primitive de g est un demi de ln de la valeur absolue de x²-3. On intègre cette fonction sur l'intervalle de e à 4 en se débarrassant de la valeur absolue. On obtient une expression avec des ln, et on simplifie si possible. Finalement, on conclut que le calcul de la valeur moyenne d'une fonction revient à faire un simple calcul d'intégrale.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Suite d'Intégrales
Une méthode pour étudier la convergence d'une suite d'intégrales est présentée dans cette transcription de vidéo. On nous donne une suite de fonctions qui vaut 1 plus t à la puissance n, et on cherche à trouver sa convergence.
La première méthode consiste à encadrer cette fonction entre 1 et 1 moins t à la puissance n. On construit des inégalités en utilisant les propriétés des fonctions croissantes et décroissantes. Cependant, cette méthode ne fonctionne pas pour la deuxième inégalité.
Donc, on utilise une deuxième méthode plus instinctive, qui consiste à faire la différence entre les deux termes de l'inégalité. On met tout au même dénominateur et on simplifie pour montrer que cette expression est positive. Ainsi, on conclut que 1 moins t à la puissance n est plus petit que 1 sur 1 plus t à la puissance n.
Ensuite, on calcule l'intégrale de 1 moins t à la puissance n de 0 à 1 en utilisant la linéarité de l'intégrale. On trouve que cette intégrale est égale à n sur n plus 1.
En utilisant l'encadrement précédemment obtenu, on déduit un encadrement pour l'intégrale im. On montre ensuite que la suite im converge vers 1 en utilisant le théorème d'encadrement.
Révisions Maths lycée
Analyse Terminale
BCPST

Introduction
Ce cours présente les intégrales, leurs applications et calculs. Il aborde des concepts plus complexes tels que la méthode d'intégration par partie pour calculer des primitives qui ne sont pas trouvées dans les tables classiques. Il explique également comment calculer des aires entre des courbes en utilisant le lien établi entre intégrales et primitives. Il aborde la définition de la valeur moyenne d'une fonction et les différentes méthodes à utiliser. En conclusion, ce cours comprend le calcul des aires sous une courbe, entre deux courbes, la valeur moyenne d'une fonction, ainsi que les méthodes spécifiques à chaque calcul. La partie la plus intéressante sera d'appliquer ces concepts à des exercices plus difficiles pour explorer les limites des calculs d'intégration par partie et d'aires.
Révisions Maths lycée
Analyse Terminale
BCPST

Intégration par Parties
Le cours présente le concept d'intégration par parties en mathématiques. L'intégration par parties est utilisée pour calculer des primitives ou résoudre des équations différentielles. La formule de base est donnée, où l'intégrale de uv' est égale à la primitive de u x v moins l'intégrale de u' x v.
La méthode consiste à choisir u et v' de manière à facil
Révisions Maths lycée
Analyse Terminale
BCPST

Aire entre 2 courbes
Dans cette vidéo, on explore comment calculer l'air entre deux courbes. Le théorème dit que si f et g sont deux fonctions continues sur un intervalle i, et que f2x est toujours plus petite que g2x, alors l'air compris entre x = a et x = b, les bords de l'intervalle, et les courbes de f et g, est égal à l'intégrale de g2x moins f2x entre a et b.
Dans l'illustration de la vidéo, on voit deux fonctions f en rouge et g en bleu. Quand f est au-dessus de g, l'air entre les courbes sur l'intervalle de x = 0,2 à environ x = 3,8 est calculée en utilisant le théorème précédent.
Après le point de croisement, où g devient au-dessus de f, l'air entre les courbes entre ce point et x = 5 est calculée en utilisant l'intégrale de g moins f.
Il est important de bien comprendre cette propriété. La vidéo a ajouté une illustration dynamique pour mieux la visualiser.
Si vous avez des questions, consultez la FAQ pour les poser. Sinon, rendez-vous dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

Valeur Moyenne
La valeur moyenne d'une fonction est définie comme étant le résultat de la division de l'intégrale de cette fonction entre deux bornes a et b par la différence entre ces deux bornes. On peut la comprendre en la comparant à une moyenne arithmétique, où la somme des valeurs est divisée par le nombre total de valeurs. Une autre façon de l'expliquer est en termes géométriques, où la valeur moyenne est équivalente à une hauteur constante sous la courbe de la fonction, qui a la même aire que la courbe elle-même. Cette notion peut être illustrée sur un graphe, où la valeur moyenne est le point où l'aire sous la courbe est égale à l'aire d'un rectangle ayant la largeur b-a et une hauteur égale à la valeur moyenne. Il est important de choisir un rectangle qui n'est ni trop bas ni trop haut pour obtenir une aire équivalente à celle de la courbe. La valeur moyenne est utilisée dans différentes méthodes et exercices, et toutes questions supplémentaires peuvent être posées dans la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Intégration par Parties : Calcul
La méthode d'intégration par partie est utilisée pour calculer certaines intégrales. La formule utilisée est l'intégrale de U'V est égale à UV moins l'intégrale de UV'. Pour se souvenir de cette formule, on peut la dériver du produit de dérivées connu, UV' égal à U'V plus UV'.
Il y a trois points importants à prendre en compte lors du choix des fonctions U et V : il doit y avoir un produit dans l'intégrale, au moins l'un des facteurs doit avoir une primitive facilement calculable, et le fait de dériver l'autre fonction doit faciliter le calcul.
Dans l'exemple donné, on souhaite calculer l'intégrale de X ln X entre 1 et E. On peut choisir U = X et V' = ln X. La primitive de U est X²/2 et la dérivée de V est 1/X. Ces choix facilitent le calcul de l'intégrale, qui se simplifie en X/2. On peut ensuite calculer cette intégrale plus facilement et obtenir le résultat E²/2 + 1/4.
Il est important de ne pas se tromper dans le choix de quelle fonction dériver et quelle fonction intégrer. Une astuce consiste à noter clairement les fonctions U', U, V et V' pour faciliter le calcul.
Cet exemple illustre comment appliquer la méthode d'intégration par partie. Si vous avez des questions, n'hésitez pas à consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Aire sous une Courbe : Calcul
Dans ce cours, nous abordons le calcul d'erreurs sous une courbe à l'aide d'intégrales. Pour illustrer cette méthode, nous prenons deux exemples.
Le premier exemple concerne l'erreur entre la courbe CF, dont l'équation est f2x = x²-4, et l'axe d'étape 6 entre les points d'équation x=-2 et x=2. En termes mathématiques, cette erreur peut être calculée en trouvant l'intégrale de x²-4 entre -2 et 2.
Nous commençons par trouver la primitive de la fonction à l'intérieur de l'intégrale. Dans ce cas, la fonction est un polynôme et donc assez facile à intégrer. La primitive est donc (1/3)x³ - 4x.
En utilisant le théorème fondamental du calcul intégral, nous pouvons calculer l'erreur comme étant la différence entre la valeur en 2 et la valeur en -2 de la primitive. Après avoir effectué les calculs, nous obtenons -32/3 comme résultat pour l'erreur.
Le graphique correspondant montre clairement que l'erreur est située en dessous de l'axe des abscisses, ce qui explique le signe négatif de -32/3. Il est important de noter que cette valeur correspond à l'erreur algébrique, tandis que la valeur absolue de l'erreur est égale à 32/3.
Dans ce cas, la variable d'intégration est x, et il est crucial de respecter la portée de cette variable. Elle varie entre -2 et 2, et ne peut pas être utilisée ailleurs.
Passons maintenant au deuxième exemple qui concerne l'erreur entre la courbe et l'axe des abscisses entre les points d'équation x=-5 et x=1. Pour calculer cette erreur, nous trouvons l'intégrale de x²-4 entre -5 et 1.
La primitive de cette fonction reste la même, mais les calculs diffèrent. Après simplification, nous obtenons 18 comme résultat pour l'erreur.
Le graphique correspondant montre que l'erreur est composée d'une partie positive et d'une partie négative. La somme des deux parties donne 18.
Ces exemples illustrent comment calculer les erreurs sous des courbes en utilisant des primitives. Si vous avez des questions supplémentaires, n'hésitez pas à consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST
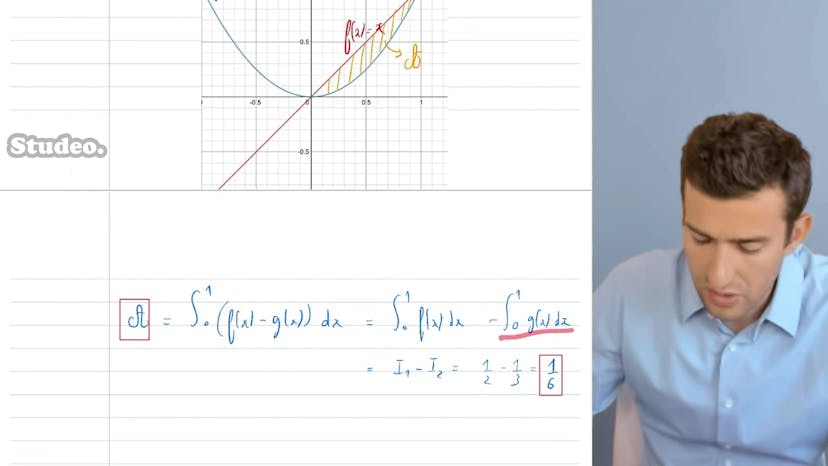
Aire entre 2 Courbes
Dans ce cours, on nous présente le calcul de l'R entre deux courbes, à savoir les fonctions f(x)=x et g(x)=x². Le but est de trouver l'R entre ces deux courbes sur l'intervalle entre x=0 et x=1.
Pour effectuer ce calcul, il est nécessaire de déterminer les primitives des deux fonctions f et g. Pour f(x)=x, la primitive est f(x)=x²/2, tandis que pour g(x)=x², la primitive est g(x)=x³/3.
En utilisant le théorème fondamental, il est possible de calculer visuellement l'R entre ces deux courbes. La fonction f est toujours supérieure à la fonction g sur l'intervalle de 0 à 1, il suffit donc de prendre la différence entre les intégrales de f et g sur cet intervalle.
En développant cette différence, on obtient l'intégrale de 0 à 1 de f moins l'intégrale de 0 à 1 de g. En utilisant les valeurs des intégrales calculées précédemment (I1=1/2 et I2=1/3), on trouve que la différence entre les deux intégrales est égale à 1/6.
Ainsi, l'R entre les deux courbes, sur l'intervalle de 0 à 1, est égal à 1/6. C'est de cette manière que l'on calcule l'R entre deux courbes.
Révisions Maths lycée
Analyse Terminale
BCPST

Calcul Valeur Moyenne
Dans ce cours, nous apprenons comment calculer la valeur moyenne d'une fonction.
La valeur moyenne d'une fonction est l'intégrale de la fonction sur un intervalle, divisée par la largeur de cet intervalle. Pour calculer cela, nous devons trouver la primitive de la fonction à intégrer.
Dans le premier exemple, nous avons la fonction f et l'intervalle de calcul est [-2, 2]. La largeur de cet intervalle est 4. En trouvant la primitive de f, nous pouvons facilement calculer l'intégrale sur cet intervalle et obtenir la valeur moyenne de f.
Dans le deuxième exemple, nous avons la fonction g et l'intervalle de calcul est [e, 4], avec e comme nombre constant. Pour calculer la valeur moyenne de g, nous devons trouver la primitive de g. En remarquant que g a une forme de quotient, nous pouvons simplifier l'intégrale en utilisant une forme comparable à "u' sur u". En trouvant la primitive de g, nous pouvons calculer l'intégrale sur cet intervalle et obtenir la valeur moyenne de g.
En appliquant la définition de la valeur moyenne et en utilisant le théorème fondamental du calcul, nous pouvons simplifier et résoudre ces calculs d'intégrales pour obtenir les expressions explicites des valeurs moyennes des fonctions f et g.
En résumé, pour calculer la valeur moyenne d'une fonction, il suffit d'appliquer la définition de l'intégrale et de trouver la primitive de la fonction.
Révisions Maths lycée
Analyse Terminale
BCPST

Suite d'Intégrales
Dans ce cours, nous étudions une suite d'intégrales et essayons de trouver sa convergence. La suite de fonctions fn est définie pour t, valant 1 sur 1 plus t à la puissance n, et l'intégrale de 0 à 1 de cette fonction est notée in.
Pour encadrer cette fonction, nous utilisons deux méthodes. La première méthode consiste à construire des inégalités. Nous constatons que 1 plus t à la puissance n est compris entre 1 et 2, et en prenant l'inverse, nous obtenons 1 sur 1 plus t à la puissance n compris entre 1 et 1,5. Cependant, cette méthode ne fonctionne pas pour l'autre inégalité.
Dans ce cas, nous utilisons la méthode de la différence. Nous prenons la différence entre 1 sur 1 plus t à la puissance n et 1 moins t à la puissance n et montrons qu'elle est positive en simplifiant. Ainsi, nous obtenons que 1 moins t à la puissance n est plus petit que 1 sur 1 plus t à la puissance n.
Nous avons donc deux encadrements pour la fonction fn. Ensuite, nous calculons l'intégrale de 0 à 1 de 1 moins t à la puissance n en utilisant la linéarité de l'intégrale. Nous obtenons 1 moins 1 sur n plus 1, que nous simplifions en n sur n plus 1.
À partir de ces résultats, nous déduisons un encadrement de l'intégrale in. En utilisant la monotonie de l'intégrale, nous calculons l'intégrale de chacune des fonctions encadrantes de 0 à 1. Ainsi, nous encadrons l'intégrale in.
Finalement, nous devons montrer que la suite in converge et donner sa limite. En réécrivant n sur n plus 1 sous la forme 1 moins 1 sur n plus 1, nous voyons que cela tend vers 1. Par conséquent, nous utilisons le théorème d'encadrement pour montrer que la suite in converge vers 1.
En conclusion, ce cours traite de méthodes pour étudier les suites d'intégrales et montre un exemple de ces méthodes en action.
Révisions Maths lycée
Analyse Terminale
ECG

Introduction
Cette vidéo d'introduction présente le nouveau sous-chapitre sur les intégrales, les applications et les calculs. Dans ce cours, nous utiliserons les connaissances précédentes pour calculer des primitives plus complexes en utilisant la méthode d'intégration par parties. Nous pourrons également calculer des aires entre des courbes en utilisant le lien entre les aires et les primitives établi dans le sous-chapitre précédent. En outre, nous étudierons la valeur moyenne d'une fonction et les différentes méthodes pour la calculer. En conclusion, ce cours abordera le calcul d'aires sous une courbe, entre deux courbes, le calcul de la valeur moyenne d'une fonction et l'intégration par parties. Nous explorerons également des exercices plus difficiles pour approfondir nos connaissances dans ces domaines. Bon courage pour cette partie du cours et n'hésitez pas à consulter la FAQ en cas de questions ou de doutes. À bientôt pour la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
ECG

Intégration par Parties
Bienvenue dans cette vidéo sur l'intégration par parties. Je vais vous présenter en détail ce sujet important du chapitre et vous montrer comment l'appliquer concrètement.
Le théorème de base de l'intégration par parties dit que l'intégrale de uv' est égale à la primitive de u x v moins l'intégrale de u' x v. Cette formule est utile lorsque l'on a des
Révisions Maths lycée
Analyse Terminale
ECG

Aire entre 2 courbes
Dans cette vidéo, nous apprenons comment calculer l'aire entre deux courbes. Le théorème nous indique que si nous avons deux fonctions continues, f et g, sur un intervalle i, et que f2x est toujours inférieur à g2x, alors l'aire entre les courbes de f et g sur l'intervalle [a, b] est égale à l'intégrale de g2x moins f2x sur cet intervalle.
L'auteur nous montre ensuite une illustration de ce théorème en utilisant deux fonctions représentées en rouge et en bleu. Il applique le théorème pour calculer l'aire lorsque f est au-dessus de g sur l'intervalle [0,2] jusqu'au point de croisement. Ensuite, il nous explique qu'après le point de croisement, il y a un changement et c'est la fonction g qui devient au-dessus. Ainsi, il applique le théorème à nouveau pour calculer l'aire entre g et f à partir du point de croisement jusqu'à 5.
La vidéo se termine en nous invitant à poser nos questions dans la FAQ et en nous donnant rendez-vous dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
ECG

Valeur Moyenne
La valeur moyenne d'une fonction est définie comme le nombre µ égal à 1 sur b-a fois l'intégrale de f entre les limites a et b, lorsque f est une fonction continue. Pour mieux comprendre cette notion, on peut la comparer à une moyenne arithmétique. L'intégrale entre a et b représente une somme infinie de rectangles infiniment petits, où chaque rectangle a une valeur correspondant à la fonction f. La somme de ces valeurs divisée par le nombre total de rectangles est similaire à la moyenne des notes de mathématiques des élèves de votre classe. Une autre façon de l'interpréter est de manière géométrique. On peut dire que µ est la valeur constante telle que l'aire sous la courbe de la fonction constante égale à µ soit égal à l'aire sous la courbe de f. Pour illustrer cela, on peut tracer un graphique représentant une fonction parabolique et la valeur moyenne correspond à la hauteur pour laquelle l'aire sous la courbe est égale à l'aire du rectangle ayant pour base la largeur de l'intervalle a-b et pour hauteur µ. Si la hauteur est trop basse, l'aire sera trop petite par rapport à l'aire sous la courbe et si la hauteur est trop élevée, l'aire sera trop grande. La valeur moyenne se situe entre ces deux extrêmes. J'espère que cela a clarifié votre compréhension de la valeur moyenne. Vous verrez dans les exercices comment l'appliquer et si vous avez des questions, n'hésitez pas à les poser.
Révisions Maths lycée
Analyse Terminale
ECG

Intégration par Parties : Calcul
La méthode d'intégration par partie est une technique pour calculer des intégrales. Cette méthode repose sur la formule suivante : l'intégrale de U'V est égale à UV moins l'intégrale de UV'. Pour faciliter la mémorisation de cette formule, on peut remarquer qu'elle provient de la dérivée du produit (UV'), qui se décompose en U'V plus UV'. En utilisant cette formule, il est important de choisir correctement les fonctions U et V. Trois points doivent être pris en compte : il faut avoir un produit dans l'intégrale, au moins l'un des deux facteurs du produit doit avoir une primitive facilement calculable, et la dérivée de l'autre fonction doit simplifier le calcul. L'objectif est d'échanger l'intégrale initiale contre une autre intégrale plus simple à calculer. Il est également possible d'appliquer l'intégration par partie dans les deux sens, mais il faut faire attention à choisir la méthode la plus avantageuse. Une astuce consiste à noter les fonctions U', U, V et V' afin de ne pas se tromper lors du calcul. Un exemple d'application de cette méthode est donné, où l'intégrale de X ln de X est calculée en utilisant l'intégration par partie. En résumé, l'intégration par partie est une méthode permettant de calculer des intégrales en utilisant une formule spécifique et en choisissant judicieusement les fonctions U et V.
Révisions Maths lycée
Analyse Terminale
ECG

Aire sous une Courbe : Calcul
Dans ce cours, nous allons parler du calcul d'erreurs sous une courbe en utilisant les intégrales. Nous utiliserons deux exemples pour calculer les erreurs sous les courbes, ce qui revient à calculer une intégrale.
Le premier exemple concerne l'erreur entre la courbe CF, avec l'équation f2x = x²-4, et l'axe d'étape 6 entre les valeurs de x égales à -2 et 2. Mathématiquement, cela peut être interprété comme l'intégrale de x²-4dx entre -2 et 2. Pour trouver la primitive de cette fonction, on pose f2x = x²-4. Étant donné que c'est un polynôme, il est facile de trouver une primitive, qui est x³/3 - 4x. Ensuite, on utilise le théorème fondamental pour calculer l'erreur, qui est égale à (x³/3 - 4x) entre les valeurs de -2 et 2. Après les calculs, on trouve une erreur de -32/3.
En utilisant un graphique, on peut visualiser que cette erreur se situe sous l'axe de la piste, ce qui explique pourquoi elle est négative. Il est important de noter que l'erreur absolue est de 32/3. De plus, cela nous donne une information importante sur la variable d'intégration, qui est x dans ce cas. Il faut faire attention à ne pas confondre la variable locale dans l'intégrale avec la variable utilisée pour définir la fonction.
Le deuxième exemple concerne l'erreur b entre la courbe et l'axe des abscisses entre les valeurs de x égales à -5 et 1. Pour calculer cette erreur, on fait l'intégrale de x²-4 entre -5 et 1. La primitive reste la même, mais les calculs sont différents. Après simplification, on trouve une erreur de 18. Visuellement, on peut voir que la partie positive de la courbe est plus grande que la partie négative, ce qui explique pourquoi l'erreur est positive.
En résumé, ce cours explique comment calculer les erreurs sous une courbe à l'aide des intégrales.
Révisions Maths lycée
Analyse Terminale
ECG
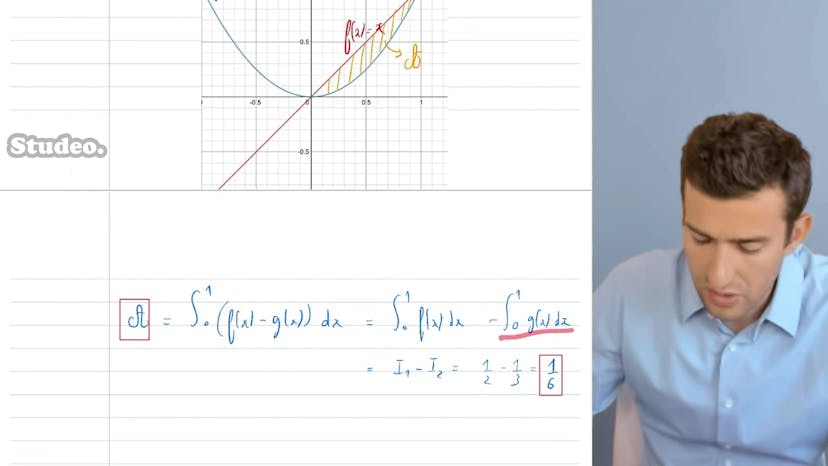
Aire entre 2 Courbes
Le calcul de l'R entre deux courbes consiste à déterminer la différence entre les intégrales des fonctions f2x et g2x sur un intervalle donné. Dans cet exemple, les fonctions f2x et g2x sont respectivement égales à x et x², et nous souhaitons calculer l'R entre x=0 et x=1.
Tout d'abord, nous devons trouver les primitives de ces deux fonctions. Une primitive de f2x est f2x = x²/2, et une primitive de g2x est g2x = x³/3.
En utilisant le théorème fondamental du calcul intégral, nous pouvons visualiser l'R entre les deux courbes. La fonction f est située en dessous de la fonction g sur tout l'intervalle, donc nous calculons l'intégrale de f2x-g2x sur l'intervalle [0, 1]. En appliquant la propriété de linéarité de l'intégrale, nous obtenons l'intégrale de f2x sur [0, 1] moins l'intégrale de g2x sur [0, 1].
En effectuant les calculs, nous obtenons que l'intégrale de f2x sur [0, 1] évaluée en 1 moins évaluée en 0 est égale à 1/2, et l'intégrale de g2x sur [0, 1] évaluée en 1 moins évaluée en 0 est égale à 1/3. Donc la différence entre les deux intégrales est égale à 1/6.
Ainsi, l'R entre les deux courbes entre x=0 et x=1 est égal à 1/6. C'est ainsi que l'on calcule l'R entre deux courbes.
Révisions Maths lycée
Analyse Terminale
ECG

Calcul Valeur Moyenne
Dans ce cours, nous apprenons comment calculer la valeur moyenne d'une fonction. Il y a deux exemples avec deux fonctions différentes, et les intervalles sur lesquels nous calculons la moyenne ne sont pas exactement les mêmes.
La valeur moyenne est définie comme l'intégrale de la fonction sur l'intervalle divisée par la largeur de l'intervalle. Par exemple, si la largeur de l'intervalle est de 4 (deux moins moins deux), alors le calcul de la valeur moyenne est simplement l'intégrale de la fonction sur cet intervalle divisée par 4.
Le problème principal est de trouver une primitive de la fonction à intégrer. Dans cet exemple, nous posons h(x) = x² + 3 et trouvons que H(x) = (1/3)*x³ + 3x est une primitive de h(x). Nous utilisons ensuite le théorème fondamental du calcul pour effectuer les calculs et obtenons une valeur de 13/3 pour la première intégrale.
Ensuite, nous voulons trouver la valeur moyenne de la fonction g(x) = x/(x² - 3), avec un intervalle de largeur 4-e. Encore une fois, le problème principal est de trouver une primitive de g(x). Nous remarquons que g(x) ressemble à un quotient, et en multipliant par 1/2*2, nous pouvons mettre la fonction sous la forme d'une dérivée logarithmique. Nous trouvons que k(x) = (1/2)*ln|x²-3| est une primitive de g(x). En effectuant les calculs, nous trouvons une expression pour la valeur moyenne qui n'est pas très agréable, mais qui a une forme explicite.
En résumé, pour calculer la valeur moyenne d'une fonction, il suffit d'appliquer la définition et de procéder à un simple calcul d'intégrale.
Révisions Maths lycée
Analyse Terminale
ECG

Suite d'Intégrales
Dans cette vidéo, nous étudions une suite d'intégrales et essayons de trouver sa convergence. Nous commençons par définir une suite de fonctions "fn" de "t" égale à 1 + "t" à la puissance "n" et "in" comme l'intégrale de 0 à 1 de "fn".
Nous essayons ensuite d'encadrer cette fonction entre 1 et 1 - "t" à la puissance "n". Nous construisons des inégalités en utilisant les propriétés des fonctions croissantes et décroissantes. Cependant, nous rencontrons des difficultés pour établir la deuxième inégalité.
Dans ce cas, nous utilisons une méthode plus intuitive en effectuant la différence entre les deux expressions. Nous parvenons à montrer que cette différence est positive, ce qui prouve que 1 - "t" à la puissance "n" est inférieur à 1 / (1 + "t" à la puissance "n").
Ensuite, nous calculons l'intégrale de 0 à 1 de 1 - "t" à la puissance "n", en utilisant la linéarité de l'intégrale. Nous trouvons que cette intégrale est égale à "n" / ("n" + 1).
En utilisant les résultats précédents, nous encadrons l'intégrale "in" entre 1 et "n" / ("n" + 1). Nous montrons ensuite que cette suite converge vers 1 en utilisant le théorème d'encadrement.
En conclusion, nous avons encadré la fonction "fn" grâce aux inégalités et calculé l'intégrale "in". Nous avons démontré que cette suite converge vers 1.


