 All subjects
All subjects
 All subjects
All subjects
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Introduction à la récurrence
Le cours introduit le principe de la méthode de démonstration par récurrence en expliquant son application aux propriétés dépendant de n. L'exemple utilisé est la formule de la somme des n entiers consécutifs. La démonstration par récurrence permet de prouver une formule dont on a déjà une intuition, en montrant que si elle est vraie à un certain rang, elle est également vraie au rang suivant. Cependant, il est important d'avoir une initialisation, c'est-à-dire un rang où la propriété est déjà vraie. Le cours propose également trois points à retenir : le principe général de la récurrence, l'initialisation qui peut commencer à un rang autre que n=0, et une inégalité classique appelée l'inégalité de Bernoulli qui peut être démontrée par récurrence. En ce qui concerne les méthodes, il est recommandé d'appliquer la récurrence aux suites, de démontrer une formule générale à partir de quelques termes connus, et de pratiquer différentes stratégies pour montrer la transmission de la propriété d'un rang à l'autre.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Concept et rédaction
Dans cette première vidéo de cours sur la récurrence, l'enseignant aborde plusieurs points importants en matière de rédaction, d'initialisation et d'erreurs à éviter.
La récurrence est une méthode de démonstration utilisée en mathématiques pour prouver qu'une propriété est vraie pour tous les entiers. Pour ce faire, on démontre d'abord que la propriété est vraie pour un entier donné, puis on montre que si elle est vraie pour un certain entier, elle est également vraie pour l'entier suivant. Ainsi, en combinant cette "pichenette initiale" et cette "transmission", la propriété est vraie pour tous les entiers.
Il est primordial de conclure la démonstration en mentionnant que la propriété est vraie pour tout entier. Omettre cette conclusion peut entraîner une perte de points dans l'évaluation. L'enseignant souligne l'importance de cette phrase de conclusion, en indiquant que certains professeurs pourraient même attribuer une note de zéro si elle est absente.
L'enseignant remarque également que dans environ 10% des exercices, la démonstration par récurrence commence par un entier différent de zéro, comme 3 ou 4. Il insiste sur le fait que le principe reste le même dans ces cas-là.
Un exemple concret de démonstration par récurrence est présenté à travers une suite numérique. L'enseignant explique les différentes étapes de la démonstration, de l'initialisation à l'hérédité en passant par la conclusion. Il rappelle aux élèves de s'adapter aux exigences de leur professeur en termes de rédaction.
En conclusion, cette vidéo met en évidence l'importance de la rédaction, de l'initialisation et de la conclusion dans la démonstration par récurrence. Elle rappelle aux élèves d'être attentifs aux spécificités de chaque exercice et de suivre les indications de leur professeur pour obtenir de bons résultats.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Pourquoi l'initialisation ?
Dans cette vidéo, l'importance de l'initialisation dans le domaine de la PitchNet est discutée. Bien que l'hérédité soit généralement considérée comme l'aspect le plus important, l'initialisation ne doit pas être négligée. Un exemple est donné pour illustrer cette importance. Le sujet abordé est la propriété P2N, qui affirme que 2 puissance N est divisible par 3. En réalité, 2 puissance N n'est pas divisible par 3, mais cette propriété peut être transmise. Il est démontré que si cette propriété est vraie pour un instant N, elle sera également vraie pour l'instant N+1. Cependant, il est souligné qu'il peut être difficile de trouver une initialisation pour cette propriété, ce qui justifie l'importance de l'initialisation dans la pratique. Cette vidéo bonus conclut en rappelant l'importance de faire l'initialisation correctement dans chaque situation.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
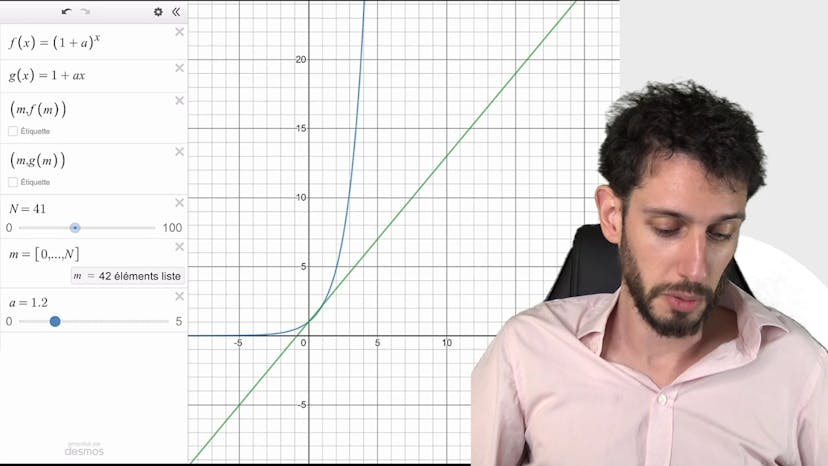
Inégalité de Bernoulli : visuel
Dans cette vidéo, le professeur cherche à expliquer graphiquement l'inégalité de Bernoulli. Il explique que cette inégalité peut être démontrée grâce au principe de récurrence. Pour mieux comprendre cette formule, il propose une simulation où il compare deux fonctions: une exponentielle et une affine. Il montre que l'exponentielle monte beaucoup plus vite que la fonction affine, ce qui justifie l'inégalité de Bernoulli. Il souligne que cette inégalité est valable pour toutes les valeurs positives de A et pour toutes les valeurs de N. Il précise également que l'inégalité est vérifiée pour les entiers 0 et 1. Il encourage les spectateurs à poser des questions et à utiliser la simulation pour mieux comprendre cette inégalité.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Récurrence et croissance
La démonstration par récurrence est une technique utilisée en mathématiques pour prouver une propriété P(n) qui est vraie pour tous les entiers naturels n. Dans cette transcription d'une vidéo, nous avons un exemple de démonstration par récurrence pour prouver que la suite donnée est strictement décroissante.
Pour commencer, nous définissons P(2n) comme la propriété qui est vraie au rang n dans la démonstration par récurrence. Dans ce cas, nous voulons montrer que Un+1 est plus petit que Un. Il est important de noter que la propriété de récurrence, P(2n), n'inclut pas la mention "pour tout n" car elle est seulement vraie pour un rang spécifique.
Nous commençons par l'initialisation, c'est-à-dire montrer que la propriété est vraie pour le premier rang (n=0). Ensuite, nous passons à l'hérédité, où nous assumons que la propriété est vraie au rang n et essayons de montrer qu'elle est également vraie au rang n+1.
Dans cet exemple, nous utilisons une relation de récurrence pour montrer l'hérédité. Nous posons la fonction f(x) = 2x - 6 et utilisons le fait que cette fonction est strictement croissante. En utilisant cette fonction, nous pouvons montrer que Un+2 est plus petit que Un+1 en composant f(Un) et f(Un+1).
En conclusion, en utilisant le principe de récurrence, nous avons prouvé que pour tout entier naturel n, Un+1 est strictement inférieur à Un, ce qui signifie que la suite est strictement décroissante.
Il est également souligné qu'il est important de distinguer entre le réel Un (la valeur de la suite au rang n) et l'objet suite Un (l'ensemble des valeurs de la suite). L'utilisation de parenthèses pour indiquer l'objet suite est recommandée pour éviter toute confusion.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Conjecture puis récurrence
Dans ce cours, nous avons vu comment utiliser une démonstration par récurrence pour calculer la somme des entiers de 1 à n. La formule à retenir est que la somme des entiers naturels de 1 à n est égale à n(n + 1)/2.
Il est important de noter que pour utiliser cette méthode de démonstration, il faut connaître le résultat que l'on souhaite démontrer. Si vous n'avez aucune idée de la valeur de la somme des entiers naturels, vous ne pourrez pas poursuivre la démonstration.
Dans cet exemple, nous allons redémontrer cette formule. Nous posons la proposition p(2n) suivante : 1 + 2 + 3 + ... + n = n(n + 1)/2. Nous supposons que p(2n) est vrai pour tout n appartenant à l'ensemble des entiers naturels.
Nous commençons par l'initialisation en vérifiant que la formule est vraie pour n = 1. En effet, 1 = 1(1 + 1)/2, donc cela est vérifié.
Ensuite, nous passons à l'hérédité. Nous supposons que p(2n) est vrai pour un certain n fixé. Nous souhaitons montrer que p(2n + 1) est également vrai, c'est-à-dire que 1 + 2 + ... + (n + 1) = (n + 1)(n + 2)/2. Pour cela, nous remplaçons chaque occurrence de n par (n + 1) dans la formule au rang n. Nous obtenons donc (n + 1)(n + 1 + 1)/2, ce qui se simplifie en (n + 1)(n + 2)/2.
Ainsi, en appliquant cette méthode de manière itérative, nous parvenons à démontrer que pour tout entier naturel non nul n, la somme des entiers de 1 à n est égale à n(n + 1)/2.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Hérédité : comment démarrer ?
La démonstration par récurrence est un point complexe dans ce cours transcrit d'une vidéo. Il y a deux cas possibles pour montrer l'hérédité. Il est préférable de bien écrire l'hypothèse de récurrence et ce que l'on souhaite démontrer, puis de faire le lien entre les deux. Deux méthodes peuvent être utilisées : partir de l'hypothèse de récurrence et aboutir à Pn+1, ou partir de Pn+1 et se servir de P2n pour conclure. Un exemple simple est donné pour illustrer la différence entre les deux méthodes. On a une suite U définie par récurrence où U0 = 5, U1+1 = 3U1 + 6, et on veut montrer que U1 est strictement positif pour tout n. On pose P2n, qui est Un strictement supérieur à 0, et on montre que P2n est vrai pour tout n. Pour l'initialisation, U0 = 5, ce qui ne pose aucun problème. Pour l'hérédité, on peut choisir de partir de l'hypothèse de récurrence et construire Un+1 à partir de cela en multipliant par 3, ou partir de Pn+1 en utilisant l'égalité Un+1 = 3Un + 6. Les deux méthodes sont possibles, mais cela dépend de l'exercice et de la préférence de chacun. Si une méthode ne fonctionne pas, il est possible d'essayer avec l'autre. Pour plus de questions, il y a une FAQ disponible.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Hérédité mais...
Ce cours porte sur une proposition mathématique et la démonstration de sa validité. L'exercice utilise le principe de récurrence pour montrer que si la propriété est vraie pour un certain rang n, alors elle est également vraie pour le rang suivant n+1. L'accent est mis sur l'importance de bien comprendre l'énoncé et de ne pas surinterpréter les informations fournies. L'exercice montre également qu'il faut prouver l'initialisation pour être sûr
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
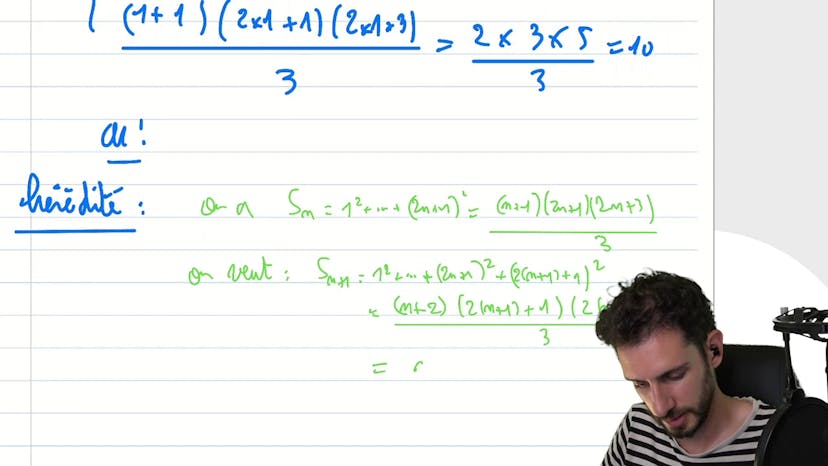
Avec une Somme
Ce cours est une transcription d'une vidéo qui explique l'importance d'écrire clairement et précisément en mathématiques. L'exemple donné est la démonstration par récurrence d'une formule mathématique. Le professeur utilise des notations et des termes spécifiques pour expliquer le processus de rédaction d'une démonstration mathématique. Il insiste sur la nécessité de suivre les consignes du professeur et de montrer clairement chaque étape du raisonnement. Le professeur utilise également des astuces pour simplifier les calculs, comme factoriser ou utiliser des notations abrégées. La conclusion est que la rédaction soignée et précise est essentielle pour éviter les erreurs et faciliter la compréhension des démonstrations mathématiques.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Majoration 'simple'
Ce cours est une transcription d'une vidéo qui traite de la démonstration par récurrence. L'objectif est de montrer que pour toute valeur de n appartenant à n étoiles, la propriété est vraie.
La démonstration commence par l'initialisation avec n=1, où l'on obtient S1=1. Ensuite, on utilise l'hérédité en supposant que la propriété est vraie pour un certain n et en démontrant qu'elle est aussi vraie pour n+1. On utilise une inégalité pour montrer que Sn+1 est inférieur ou égal à 2-1/n+1.
En utilisant des manipulations algébriques, on montre que l'inégalité est vraie et donc que la propriété est héréditaire.
En conclusion, on peut affirmer que la propriété est démontrée pour tout n appartenant à n étoiles. Cependant, il est important d'écrire une conclusion pour éviter de perdre des points lors de l'évaluation.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Trop de puissance !
Ce cours concerne une suite définie par un terme initial u0 et une relation de récurrence. Le processus pour calculer les termes de la suite consiste en deux étapes : d'abord avoir une intuition du résultat en calculant u1, u2, u3, etc., puis démontrer cette intuition par récurrence. Pour cela, on écrit une formule générale basée sur les premiers termes de la suite et on la démontre. Dans cet exemple, on montre que la suite est égale à u0 puissance 2 puissance n. On commence par l'initialisation avec n=0, où la formule se simplifie à u0. Ensuite, on utilise la récurrence pour démontrer que Pn implique Pn+1. La démonstration de la récurrence dans cet exemple est assez simple, mais il est important de comprendre la méthode générale pour résoudre ce type d'exercice, en utilisant des intuitions, des essais de premiers termes et des démonstrations par récurrence. Ces compétences seront utiles non seulement pour le supérieur, mais aussi pour le bac.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Majoration plus costaude
Ce cours est une transcription d'une vidéo sur les démonstrations récursives en mathématiques. Il aborde les concepts de récurrence, d'initialisation et d'hérédité, ainsi que les manipulations des équations trigonométriques. L'orateur insiste sur l'importance de connaître les formules et d'être capable de poser les bonnes questions pour résoudre les problèmes mathématiques.
Révisions Maths lycée
Analyse Terminale
BCPST

Introduction à la récurrence
Dans cette vidéo, nous allons vous introduire le principe de la méthode de démonstration par récurrence. Cette méthode s'applique uniquement aux propriétés qui dépendent de n, principalement utilisée dans le chapitre des suites. Bien que cette méthode soit souvent appliquée sans trop de difficulté, il est important de comprendre pourquoi elle fonctionne réellement.
Nous allons utiliser un exemple classique pour expliquer cela, la formule de la somme des n entiers consécutifs. Cette formule peut être exprimée de manière compacte, en multipliant le dernier entier à sommer par le suivant, n+1, et en divisant le tout par 2. La démonstration par récurrence ne va pas vous fournir une formule à partir de rien, mais plutôt permettre de prouver une formule pour laquelle vous avez déjà une intuition.
Il est souvent nécessaire de faire des calculs pour des cas particuliers, comme n = 0, n = 1, n = 2, afin de vérifier que la formule se vérifie bien. Une fois que vous avez cette intuition, vous pouvez utiliser la démonstration par récurrence. L'idée est de prouver que si la propriété est vraie à un certain stade, elle sera aussi vraie à l'étape suivante. Ainsi, il n'est pas nécessaire de prouver la propriété pour chaque valeur de n individuellement.
Il est important de noter qu'il faut une "pitch net" initiale pour que la démonstration par récurrence fonctionne. Cela signifie qu'il doit exister un moment où la propriété est vraie. Par exemple, si la propriété est vraie pour n = 0 et qu'elle implique la propriété pour n = 1, 2, 3, etc., alors la démonstration par récurrence est valide.
En résumé, il y a trois points importants à retenir de ce cours. Premièrement, connaître le principe général de l'initialisation et de l'hérédité dans la démonstration par récurrence. Deuxièmement, comprendre que l'initialisation peut commencer à n = 0 ou à une autre valeur. Et enfin, savoir utiliser la démonstration par récurrence dans des exemples concrets, comme les suites ou la démonstration d'une formule générale.
Il est également important de comprendre les différentes façons de montrer la transmission de la propriété d'un rang à l'autre, ce qui nécessite de la pratique et de l'expérience. Cela vous permettra d'être à l'aise avec cette méthode et d'obtenir de bons résultats dans vos démonstrations.
Voilà, c'est tout pour cette introduction. À bientôt dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

Concept et rédaction
Dans cette vidéo, le professeur explique le concept de démonstration par récurrence. Il commence par rappeler que pour démontrer une propriété par récurrence, il faut montrer qu'elle est vraie pour un entier donné, et que si elle est vraie pour un entier, alors elle est aussi vraie pour l'entier suivant. Il souligne l'importance de l'initialisation et des erreurs à éviter.
Le professeur explique que la démonstration par récurrence peut être traduite en mathématiques par le fait que si une propriété P est vraie pour un entier n=0, et si elle est transmissible de l'entier n à l'entier n+1, alors la propriété P est vraie pour tous les entiers. Il met en garde contre l'oubli de la conclusion dans la démonstration, qui peut entraîner une perte de points lors de l'évaluation.
Le professeur donne ensuite un exemple concret pour illustrer la démonstration par récurrence. Il présente une suite récurrente et montre comment démontrer que la propriété P est vraie pour tous les entiers n+2. Il souligne également que dans certains cas, la démonstration peut commencer avec un entier différent de zéro, et que le principe reste le même.
Le professeur conclut en rappelant l'importance de suivre les consignes du professeur et en encourageant les étudiants à poser des questions supplémentaires si nécessaire.
Révisions Maths lycée
Analyse Terminale
BCPST

Pourquoi l'initialisation ?
Dans cette vidéo, l'importance de l'initialisation dans la PitchNet est discutée. L'orateur explique qu'à première vue, l'initialisation peut sembler insignifiante, mais il donne un exemple pour illustrer son importance. Il évoque la propriété P2N, qui affirme que 2 puissance N est divisible par 3. Il souligne que normalement, cela n'est pas vrai, car 2 puissance N ne contient pas de facteur 3. Cependant, il explique que cette propriété peut être transmise, c'est-à-dire que si elle est vraie à un certain moment, elle peut aussi être vraie plus tard. Il développe cette idée en montrant que si 2 puissance N est divisible par 3, alors 2 puissance N plus 1 est aussi divisible par 3. Toutefois, il précise que pour que cette propriété puisse être utilisée, il faut une initialisation appropriée, ce qui peut être difficile à obtenir. Il conclut en soulignant l'importance d'être complet et de prendre en compte l'initialisation dans la résolution de problèmes.
Révisions Maths lycée
Analyse Terminale
BCPST

Inégalité de Bernoulli : visuel
Dans cette vidéo, le cours aborde l'inégalité de Bernoulli, qui affirme que pour tout nombre réel positif A et tout nombre entier N, l'inégalité suivante est vérifiée : 1 + A^N ≥ 1 + NA. Cette inégalité est étudiée dans le cadre de la récurrence, car il est facile de la démontrer en utilisant le principe de récurrence.
Pour donner une intuition graphique de cette formule, le professeur l'analyse en termes de fonctions. Plus précisément, il compare la fonction 1 + A^X à la fonction 1 + AX. L'idée est que la fonction exponentielle (1 + A^X) monte beaucoup plus rapidement que la fonction affine (1 + AX), ce qui explique pourquoi 1 + A^N est toujours plus grand ou égal à 1 + NA.
Le professeur utilise une simulation graphique pour illustrer cette idée. Il affiche les deux fonctions (1 + A^X en bleu et 1 + AX en vert) en fonction de la valeur de A, qu'il peut ajuster. En déplaçant la valeur de A, on observe que les fonctions évoluent différemment. La fonction exponentielle 1 + A^X a une croissance exponentielle, tandis que la fonction affine 1 + AX a une croissance linéaire.
En s'approchant de certaines valeurs de A, on peut voir que la fonction exponentielle est toujours au-dessus de la fonction affine. Cependant, entre 0 et 1, la fonction affine semble être parfois au-dessus de la fonction exponentielle. Cela montre que l'inégalité n'est pas toujours vérifiée pour tous les nombres réels entre 0 et 1. Cependant, pour les entiers, les deux fonctions sont égales pour les valeurs 0 et 1.
Le professeur souligne que l'intérêt de cette inégalité réside dans son application dans les démonstrations mathématiques. Elle repose sur une réalité de fonction que l'on connaît bien, ce qui facilite sa compréhension et son utilisation. Il encourage les élèves à poser des questions et à consulter la Foire Aux Questions (FAQ) pour plus d'informations. Une simulation graphique est également mise à leur disposition pour les aider à comprendre cette inégalité.
Révisions Maths lycée
Analyse Terminale
BCPST

Récurrence et croissance
La démonstration par récurrence est une méthode utilisée en mathématiques pour prouver qu'une propriété est vraie pour tous les rangs d'une suite. Dans cet exemple, nous devons montrer par récurrence que la suite est strictement décroissante.
Pour ce faire, nous commençons par définir la propriété P2n, qui est vraie au rang n. Dans ce cas, nous devons montrer que Un+1 est plus petit que Un.
Nous commençons par l'initialisation en calculant les premiers termes de la suite (U0 et U1) pour vérifier la propriété au premier rang. Ensuite, nous utilisons l'hypothèse de récurrence pour montrer que la propriété est vraie pour le rang suivant (n+1).
Dans cet exemple, nous utilisons une fonction affine f(x) = 2x - 6 pour montrer la propriété. Nous constatons que cette fonction est strictement croissante, ce qui nous permet de conclure que Un+2 est plus petit que Un+1.
En utilisant le principe de récurrence, nous concluons que la suite est strictement décroissante pour tous les rangs n. Il est important d'utiliser des parenthèses pour distinguer entre le réel Un et l'objet suite Un.
Révisions Maths lycée
Analyse Terminale
BCPST

Conjecture puis récurrence
La vidéo porte sur la démonstration par récurrence pour calculer la somme des entiers de 1 à n. La formule à connaître est que la somme des entiers naturels de 1 à n est égale à n(n+1)/2. Il est important de connaître le résultat que l'on souhaite démontrer pour utiliser cette méthode. On suppose la proposition p2n valide pour tout n appartenant à n étoiles, mais cela ne s'applique pas pour n égal à 0. On commence par l'initialisation où la formule est validée pour n=1. Ensuite, on utilise l'hérédité en supposant que p2n est vrai pour un n quelconque. On souhaite montrer que p2n+1 est vrai, c'est-à-dire que la somme des entiers de 1 à n+1 est égale à (n+1)(n+2)/2. On remplace chaque n dans l'expression p2n par n+1 pour obtenir p2n+1. On applique la formule de récurrence p2n pour montrer que p2n+1 est vrai. On factorise par n+1 dans l'expression et on obtient (n+1)(n+2)/2, ce qui prouve l'hérédité. Ainsi, selon le principe de récurrence, la somme des entiers de 1 à n est égale à n(n+1)/2 pour tout n non nul.
Révisions Maths lycée
Analyse Terminale
BCPST

Hérédité : comment démarrer ?
La démonstration par récurrence est utilisée pour montrer l'hérédité dans un problème donné. Il existe deux méthodes possibles pour faire le lien entre l'hypothèse de récurrence et ce que l'on veut démontrer.
Dans l'exemple donné, la suite est définie par récurrence avec U0=5 et Un+1=3Un+6. L'objectif est de montrer que Un est strictement positif pour tout n.
Pour cela, on pose P2n comme hypothèse, c'est-à-dire que Un est strictement supérieur à 0. On va montrer que P2n est vrai pour tout n.
Dans la phase d'initialisation, aucun problème n'est rencontré car U0=5.
Ensuite, vient la phase d'hérédité. On part de l'hypothèse P2n, c'est-à-dire que Un est supérieur à 0, et on veut montrer que Pn+1 est vrai, c'est-à-dire que Un+1 est supérieur à 0.
On peut utiliser deux méthodes possibles pour cela. Soit on part de l'hypothèse de récurrence et on construit Un+1 à partir de Un en multipliant par 3. Ainsi, 3Un+6 est supérieur à 6, qui est lui-même supérieur à 0. Donc Un+1 est supérieur à 0.
Sinon, on peut partir de Pn+1 directement, c'est-à-dire Un+1, et dire que Un+1=3Un+6. Comme Un est supérieur à 0, tout ce qui est supérieur à 0 est également vrai. Donc Un+1 est supérieur à 0.
Les deux méthodes sont possibles, cela dépend de l'exercice. Si on rencontre des difficultés avec une méthode, on peut essayer l'autre.
En conclusion, la démonstration par récurrence permet de montrer l'hérédité dans un problème donné en utilisant deux méthodes possibles. Si des questions subsistent, il est conseillé de consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Hérédité mais...
Le cours porte sur la démonstration d'une propriété mathématique à l'aide de la récurrence. La question 1 demande de montrer que si la propriété est vraie pour un certain entier n, alors elle est aussi vraie pour n+1. L'élève explique qu'il faut se concentrer sur l'hérédité plutôt que sur l'initialisation, et utilise cette méthode pour montrer que la proposition est vraie pour n+1.
Dans la question 2, l'élève doit montrer si la propriété
Révisions Maths lycée
Analyse Terminale
BCPST
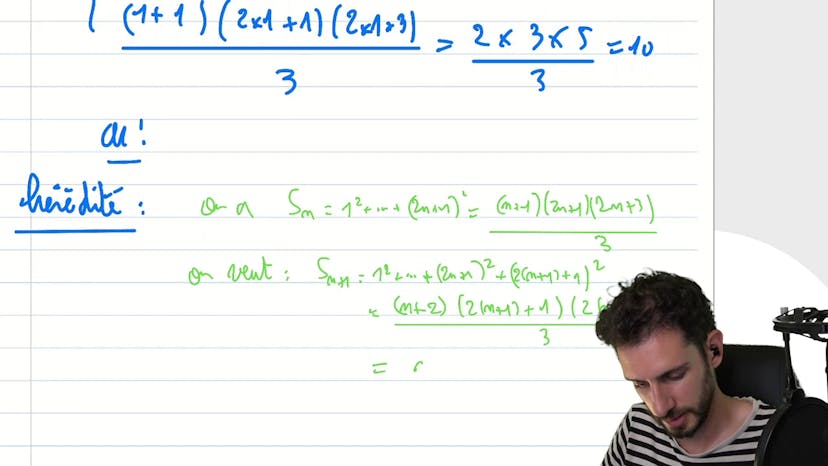
Avec une Somme
Dans ce cours, il est expliqué l'importance d'écrire ce que l'on veut. Le cours concerne une démonstration mathématique et l'orateur utilise des exemples concrets pour expliquer chaque étape. Il commence par définir une somme de nombres impairs et l'appelle SN. Ensuite, il démontre par récurrence que la somme SN plus 1 équivaut à une certaine expression, en utilisant une hypothèse de récurrence et en effectuant une factorisation. En conclusion, l'orateur souligne l'importance de prendre le chemin le plus efficace pour éviter les erreurs. La démonstration est réalisée de manière fluide et compréhensible.
Révisions Maths lycée
Analyse Terminale
BCPST

Majoration 'simple'
Ce cours porte sur une démonstration mathématique par récurrence. L'auteur montre que pour tout n appartenant à l'ensemble des entiers naturels, une certaine propriété est vraie. La démonstration se fait en deux étapes: l'initialisation et l'hérédité.
Dans l'initialisation, l'auteur vérifie que la propriété est vraie pour n=1. Il trouve que cela est en effet le cas.
Dans l'étape d'hérédité, l'auteur suppose que la propriété est vraie pour n=k, puis il cherche à prouver qu'elle est également vraie pour n=k+1.
Pour cela, il écrit l'expression de S(k+1) en utilisant l'hypothèse de récurrence, puis il simplifie cette expression pour la comparer à ce qu'il veut montrer. Il utilise une règle d'inégalité et une règle de simplification pour arriver à la conclusion que S(k+1) est inférieur ou égal à 2 - 1/(k+1).
En conclusion, l'auteur démontre que la propriété est vraie pour tout n appartenant à l'ensemble des entiers naturels.
Révisions Maths lycée
Analyse Terminale
BCPST

Trop de puissance !
Ce cours porte sur la résolution de suites définies par une relation de récurrence. L'auteur explique qu'il y a deux étapes principales dans ce processus: l'intuition du résultat et la démonstration de cette intuition par récurrence. Il utilise un exemple concret pour illustrer ces étapes.
L'auteur commence par donner la relation de récurrence de la suite et explique qu'il faut d'abord avoir une intuition du résultat en calculant les premiers termes de la suite. Ensuite, il montre comment cette intuition peut être démontrée par récurrence en utilisant une hypothèse sur le terme général de la suite et une démonstration par récurrence pour prouver cette hypothèse.
Il explique également que pour résoudre ce type d'exercice, il est important de faire des essais sur les premiers termes de la suite et d'essayer différentes approches pour arriver à une solution. Il souligne l'importance de savoir se dépatouiller dans ce genre d'exercice et de savoir faire preuve de créativité et d'initiative.
En conclusion, l'auteur souligne l'importance de développer des compétences en résolution de problèmes mathématiques, en particulier dans les situations où les indications sont limitées. Il encourage les étudiants à apprendre à gérer ces situations et à utiliser des stratégies de résolution adaptées.
Révisions Maths lycée
Analyse Terminale
BCPST

Majoration plus costaude
Ce cours concerne la démonstration d'une relation mathématique à l'aide de la récurrence. L'exemple utilisé est le cas où n égale 0. En utilisant la valeur absolue du sinus de 0 et du sinus d'un réel quelconque, il est démontré que le côté gauche de l'équation est égal à 0. Ensuite, l'étape d'hérédité est abordée, dans laquelle une formule mathématique est introduite pour démontrer l'inégalité souhaitée. Cette partie du cours souligne l'importance de connaître les formules mathématiques et de savoir les appliquer correctement. En fin de compte, la démonstration est réalisée grâce à la récurrence et à l'utilisation d'inegalités et de majorations. Le cours insiste sur l'importance de poser les bonnes questions et de maîtriser les notions fondamentales des mathématiques pour réussir dans ce domaine.
Révisions Maths lycée
Analyse Terminale
ECG

Introduction à la récurrence
Dans cette vidéo, le cours introduit le principe de la méthode de démonstration par récurrence. Cette méthode s'applique aux propriétés qui dépendent de n, ce qui justifie sa place dans le chapitre des suites. L'auteur remarque que les étudiants réussissent souvent à l'appliquer sans difficulté, mais sans véritable compréhension du pourquoi cela fonctionne. Il prend l'exemple de la formule de la somme des n entiers consécutifs pour expliquer le processus de démonstration par récurrence.
La démonstration par récurrence ne permet pas de trouver une formule, mais plutôt de démontrer une formule dont on a déjà une intuition. Il est souvent nécessaire de faire des calculs pour certains n afin de comprendre comment la propriété dépend de n. Une fois que l'intuition est claire, il est possible de démontrer la formule par récurrence.
La méthode consiste à montrer que si la propriété est vraie à un certain n, alors elle est également vraie au n+1. Si cette transmission de propriété est établie, il n'est pas nécessaire de prouver la formule pour tous les n individuellement.
Cependant, il est important d'avoir une initialisation, c'est-à-dire un cas de base où la propriété est vraie (par exemple, pour n=0) et de pouvoir prouver que cette initialisation implique la véracité de la propriété pour n+1 et les n suivants.
Le cours souligne également que la méthode de récurrence peut s'appliquer à d'autres problèmes, tels que la démonstration de l'inégalité de Bernoulli. Il offre également trois exemples d'application de la récurrence, notamment dans le domaine des suites et pour la démonstration de formules générales.
En résumé, ce cours introduit le principe de la méthode de démonstration par récurrence, explique comment elle fonctionne et donne des exemples d'application. Il souligne l'importance de l'initialisation et de la transmission de la propriété d'un rang à l'autre.
Révisions Maths lycée
Analyse Terminale
ECG

Concept et rédaction
Ce cours porte sur la récurrence et met l'accent sur l'importance de la rédaction, de l'initialisation et des erreurs à éviter. Pour démontrer une propriété par récurrence, il faut montrer qu'elle est vraie pour un entier donné, puis montrer qu'elle est vraie pour l'entier suivant. La combinaison de ces deux éléments permet d'établir la vérité de la propriété pour tous les entiers. Il est essentiel de conclure en indiquant que la propriété est vraie pour tout entier, sinon des points seront perdus. Dans cette vidéo, il est également souligné que dans environ 10% des exercices, le même processus est appliqué mais en commençant par un nombre différent de zéro. Un exemple de suite récurrente est donné pour illustrer cela. Le cours mentionne également l'importance de suivre les consignes du professeur en termes de vocabulaire et de rédaction. Les étapes de l'initialisation et de l'hérédité sont expliquées, et une conclusion est donnée pour résumer la démonstration. Si des questions subsistent, il est conseillé de consulter la FAQ ou de poser une question pour obtenir des clarifications supplémentaires.
Révisions Maths lycée
Analyse Terminale
ECG

Pourquoi l'initialisation ?
Dans cette vidéo, l'importance de la PitchNet initiale en SEO friendly est abordée. L'orateur mentionne qu'il pensait que l'initialisation était inutile et fastidieuse, mais il explique qu'il existe des propriétés qui peuvent être transmises même si elles ne sont jamais vraies.
Il donne l'exemple de la propriété P2N, qui représente le fait que 2 puissance N est divisible par 3. Il explique que normalement, 2 puissance N n'est pas divisible par 3. Cependant, il explique qu'en considérant uniquement la transmission de la propriété, sans se préoccuper de sa véracité, on peut imaginer un instant où cette propriété est vraie.
Il montre ensuite que si 2 puissance N est divisible par 3, alors 2 puissance N plus 1 est également divisible par 3. Il conclut en soulignant l'importance de faire une initialisation complète à chaque fois, car il est possible qu'une propriété fausse ait la propriété de transmission.
Il termine en encourageant les spectateurs à poser des questions et en indiquant que la FAQ est disponible.
Révisions Maths lycée
Analyse Terminale
ECG

Inégalité de Bernoulli : visuel
Dans cette première vidéo, le professeur explique l'inégalité de Bernoulli, qui stipule que pour tout réel positif A et tout nombre entier N, on a l'inégalité suivante : 1 + A^N >= 1 + NA. Il explique que cette inégalité est étudiée dans le chapitre de la récurrence car la démonstration par récurrence est simple. Il mentionne également que certains étudiants ont du mal à comprendre cette formule et propose une explication graphique. En utilisant des fonctions exponentielles et affines, il visualise graphiquement comment l'exponentielle monte plus rapidement que l'affine, ce qui justifie l'inégalité. Il montre ensuite une simulation où il peut manipuler les paramètres pour illustrer le comportement des fonctions. Il remarque que pour certains réels entre 0 et 1, l'affine est au-dessus de l'exponentielle, ce qui peut sembler contredire l'inégalité. Cependant, il souligne que pour les entiers, l'inégalité est vérifiée et que cela a une signification pratique. Il conclut en encourageant les spectateurs à poser des questions et à utiliser la simulation pour mieux comprendre l'inégalité de Bernoulli.
Révisions Maths lycée
Analyse Terminale
ECG

Récurrence et croissance
La démonstration par récurrence est une méthode utilisée en mathématiques pour prouver qu'une propriété est vraie pour tous les termes d'une suite. Voici les étapes de cette méthode :
1. Définir la propriété P(2n) qui est vraie pour le terme au rang n. Dans notre exemple, nous voulons prouver que la suite est strictement décroissante, donc nous devons montrer que Un+1 < Un.
2. Commencer par l'initialisation en montrant que la propriété est vraie pour le premier terme. Dans notre exemple, nous calculons U1 et U0 pour vérifier cette condition.
3. Supposer que la propriété est vraie pour le terme Un, c'est-à-dire que P(n) est vrai.
4. Montrer que la propriété est vraie pour le terme Un+1, c'est-à-dire P(n+1) est vrai. Dans notre exemple, nous utilisons la relation de récurrence Un+1 = 2Un - 6.
5. Utiliser une fonction affine f(x) = 2x - 6 pour simplifier la démonstration. Cette fonction est strictement croissante, donc si Un+1 < Un, alors f(Un+1) < f(Un).
6. Conclure que la propriété est vraie pour tous les termes de la suite en utilisant le principe de récurrence.
Il est important de bien préciser que Un représente le terme de la suite, tandis que U(n) représente l'objet suite. Il est préférable d'utiliser des parenthèses lorsqu'on parle de la suite pour éviter toute confusion.
En résumé, la démonstration par récurrence est une méthode utilisée pour prouver qu'une propriété est vraie pour tous les termes d'une suite. Dans notre exemple, nous avons montré que la suite est strictement décroissante en suivant les étapes de cette méthode.
Révisions Maths lycée
Analyse Terminale
ECG

Conjecture puis récurrence
Dans ce cours, nous étudions comment utiliser la démonstration par récurrence pour calculer la somme des entiers de 1 à n.
La formule pour calculer la somme des entiers naturels est nn plus 1 sur 2.
Pour utiliser la démonstration par récurrence, il est important de connaître le résultat que nous voulons démontrer, c'est-à-dire la formule de la somme des entiers naturels.
Nous supposons que la proposition p2n est vraie pour tout n appartenant à n étoiles. La proposition p2n est que la somme des entiers de 1 à n est égale à nn plus 1 sur 2.
Nous commençons par vérifier l'initialisation, c'est-à-dire lorsque n est égal à 1. Dans ce cas, la somme est simplement 1, ce qui correspond bien à nn plus 1 sur 2.
Ensuite, nous passons à l'hérédité. Nous supposons que p2n est vraie et nous voulons montrer que p2n plus 1 est vraie. Pour cela, nous remplaçons chaque n par n plus 1 dans l'expression de p2n. Par exemple, nn plus 1 devient (n plus 1)(n plus 1) plus 1 sur 2. Nous développons cette expression et nous obtenons (n plus 1)(n plus 2) sur 2, ce qui est équivalent à p2n plus 1.
Nous avons donc démontré que pour tout n appartenant à n étoiles, la somme des entiers de 1 à n est égale à nn plus 1 sur 2.
Cela conclut notre exemple de démonstration par récurrence pour la formule de la somme des entiers naturels.
Révisions Maths lycée
Analyse Terminale
ECG

Hérédité : comment démarrer ?
La démonstration par récurrence est une méthode utilisée en mathématiques pour prouver une propriété Pn pour tous les entiers n d'une suite définie par récurrence. Pour démontrer l'hérédité, il existe deux cas de figure :
- Le premier cas consiste à partir de l'hypothèse de récurrence (Un > 0) et à construire Un+1 à partir de cela. Par exemple, en multipliant Un par 3 et en ajoutant 6, on obtient 3Un + 6 > 6 > 0, ce qui prouve que Un+1 est également strictement positif.
- Le deuxième cas consiste à partir de ce que l'on veut montrer (Un+1 > 0) et à utiliser la propriété P2n pour conclure. Par exemple, si Un+1 = 3Un + 6 et Un > 0, alors 3Un + 6 > 0, ce qui prouve que Un+1 est bien positif.
Ces deux méthodes sont possibles et peuvent être utilisées en fonction de l'exercice. Si vous rencontrez des difficultés avec l'une des méthodes, vous pouvez essayer l'autre pour voir si cela fonctionne mieux.
Révisions Maths lycée
Analyse Terminale
ECG

Hérédité mais...
Cet exercice de mathématiques consiste à prouver une proposition pour tout nombre entier naturel n en utilisant le principe de la récurrence. Plus précisément, il s'agit de démontrer que si la proposition est vraie pour un rang n, alors elle est également vraie pour le rang n+1. L'exercice met en avant l'importance de bien lire l'énoncé et de ne pas surinterpréter les informations données. L'élève doit trouver une manière d
Révisions Maths lycée
Analyse Terminale
ECG
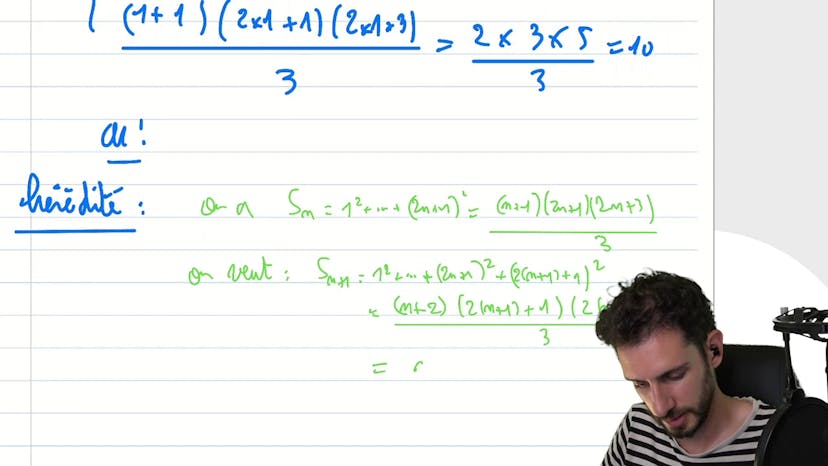
Avec une Somme
Ce cours traite de la démonstration d'une égalité en utilisant le principe de récurrence. L'auteur explique qu'il est important de suivre les instructions du professeur et d'écrire ce qu'on veut démontrer. Ensuite, il montre comment utiliser l'initialisation et l'hérédité pour prouver l'égalité. L'auteur utilise des notations mathématiques et fait des calculs pour démontrer chaque étape. Finalement, il conclut en montrant que l'égalité est démontrée.
Révisions Maths lycée
Analyse Terminale
ECG

Majoration 'simple'
Ce cours porte sur une démonstration mathématique par récurrence. L'objectif est de prouver que pour tout entier n appartenant à l'ensemble des entiers naturels, une certaine propriété est vraie.
Le professeur commence par expliquer les étapes de la démonstration, en utilisant des notations pour faciliter la compréhension. Il rappelle l'importance de nommer les différentes parties de la démonstration.
Ensuite, le professeur procède par récurrence en commençant par n = 1. Il montre que la propriété est vraie pour n = 1 en effectuant les calculs nécessaires.
Ensuite, il aborde l'étape de l'hérédité de la démonstration. Il écrit une expression avec une somme en fonction de n et montre comment il peut utiliser cette expression pour prouver que la propriété est vraie pour n+1.
Il utilise des étapes de logique et des règles mathématiques pour simplifier l'expression et finalement prouver que la propriété est vraie pour n+1.
Le professeur insiste sur l'importance de bien nommer chaque étape de la démonstration et de fournir une conclusion claire.
En résumé, ce cours explique comment utiliser la méthode de récurrence pour prouver qu'une propriété mathématique est vraie pour tous les entiers naturels. Le professeur décompose les étapes de la démonstration et montre comment simplifier les expressions pour arriver à la conclusion souhaitée.
Révisions Maths lycée
Analyse Terminale
ECG

Trop de puissance !
Ce cours traite de la démonstration d'une suite définie par une relation de récurrence, avec le grand principe de chercher des indices en calculant les premiers termes. L'exemple utilisé est une suite définie par un terme initial au hasard, et le processus de démonstration consiste en deux étapes : l'intuition du résultat en calculant les termes suivants, suivie de la démonstration de cette intuition par récurrence. L'objectif est de montrer que Pn implique Pn+1, et la récurrence est démontrée en utilisant la formule de la suite et en justifiant chaque égalité. Il est souligné que cette démarche est importante pour les élèves qui poursuivront dans l'enseignement supérieur, car il faut savoir se débrouiller face à des problèmes moins guidés.
Révisions Maths lycée
Analyse Terminale
ECG

Majoration plus costaude
Ce cours est une transcription d'une vidéo expliquant la démonstration d'une récurrence mathématique. Dans cette démonstration, on utilise le fait que le sinus de 0 fois tout réel est égal à 0, et que le produit de 0 par la valeur absolue de sinus x est également égal à 0. On vérifie également l'initialisation de la récurrence. Ensuite, on aborde la notion d'hérédité et on utilise une formule mathématique appelée "sin a plus b" pour faire apparaître sin nx. On applique ensuite l'inégalité triangulaire pour majorer les termes et on utilise le fait que les cosinus sont toujours plus petits que 1. On conclut que la relation est démontrée par récurrence. L'accent est mis sur la capacité à poser les bonnes questions et à utiliser les formules mathématiques pour résoudre les problèmes.


