Online Généralités et Fonctions de Référence course by Top Instructors - Généralités et Fonctions de Référence

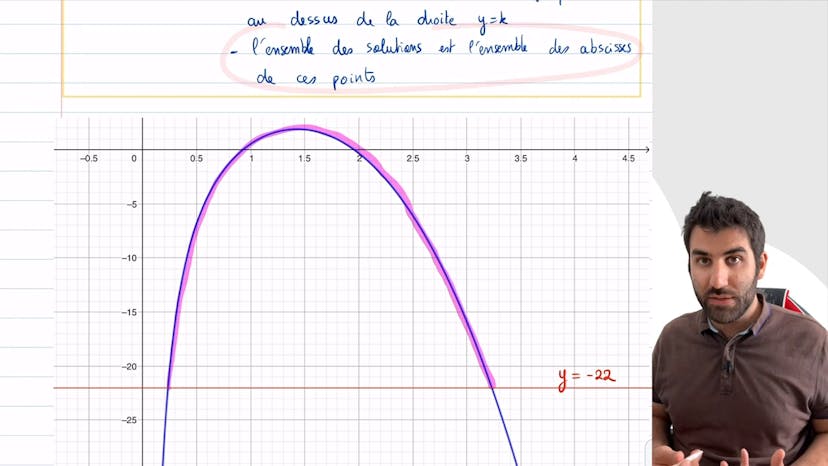
Résolution graphique : inéquation

Dans cet article, nous allons voir comment résoudre une inéquation graphiquement en trois étapes. Premièrement, nous devons tracer la courbe de la fonction f(x) supérieure à k. Deuxièmement, nous traçons la droite d'équation y=k. Enfin, nous repérons l'ensemble des points de la courbe au-dessus de la droite pour trouver l'ensemble des abscisses qui nous intéressent. Dans notre exemple, nous trace la courbe de f(x), traçons la droite y=-22, repérons l'ensemble des points au-dessus de la droite, puis nous trouvons que l'intervalle de solution graphique est entre 0,22 et 3,23.

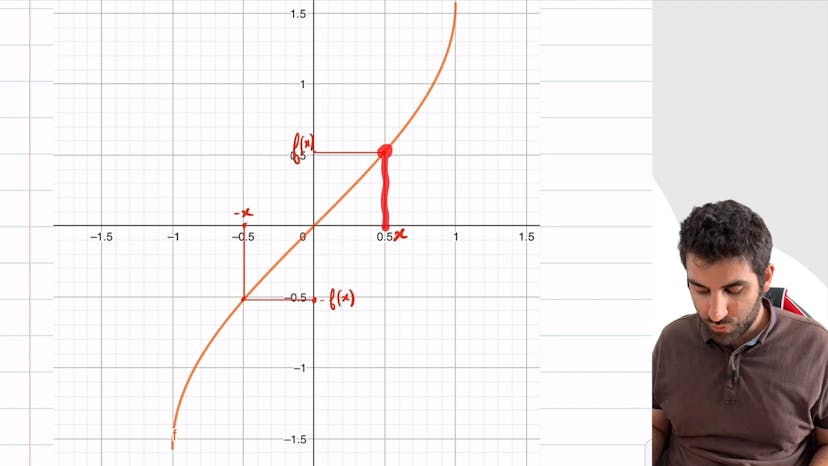
Parité d'une fonction

Cet exercice porte sur la détermination graphique de la parité d'une fonction, que ce soit paire ou impaire. Pour qu'une fonction soit paire, son ensemble de définition doit être centré en 0, et f de moins x doit être égal à f de x. En revanche, pour qu'une fonction soit impaire, son ensemble de définition doit être également centré en 0, mais cette fois-ci, f de moins x est égal à moins f de x. Pour le déterminer graphiquement, on peut prendre deux antécédents, les tracer sur le graphique, retrouver leur image, et observer si f de moins x est égal à f de x ou à moins f de x. Dans l'exemple donné, la fonction arcthynus est impaire.

Tracer une fonction symétrique

Dans cet exercice, nous apprenons à tracer la courbe symétrique par rapport à la première bissectrice d'une autre courbe. La première bissectrice est une droite qui passe par des points ayant la même abscisse que l'ordonnée. Pour tracer une courbe, nous devons faire un tableau de valeurs qui nous donne les coordonnées des points, que nous placon sur un graphique et nous les relions pour former la courbe. Pour trouver la courbe symétrique, nous devons inverser les coordonnées de la courbe initiale par rapport à l'axe Y = X. Nous faisons ensuite un tableau de valeurs de ces points qui nous donneront les nouvelles coordonnées. Nous plaçons ces points sur un graphique, en renversant l'axe des ordonnées et des abscisses et les reliant pour former notre courbe symétrique. Dans cet exercice, notre courbe symétrique est celle de la fonction racine carré.

Trouver un antécédent

Dans cet exercice de mathématiques, on apprend comment trouver les antécédents d'un nombre par une fonction en résolvant l'équation f(x) = k. Dans l'exemple présenté, la fonction f(x) est explicitement définie comme 2x + 7 au carré moins 4 et on cherche à trouver les antécédents de 6. Après avoir résolu l'équation, on factorise l'expression pour obtenir un produit de facteurs nul et on trouve deux solutions possibles : x = racine de 5 moins 7 et x = moins racine de 5 moins 7. Ces solutions représentent les antécédents de 6 par la fonction f.

Antécédent et Image

Dans cette leçon, nous apprenons comment savoir si un point appartient à la courbe d'une fonction en utilisant ses coordonnées. Si un point M a des coordonnées xm, ym et appartient à la courbe d'une fonction, alors l'ordonnée de M est égale à f de son abscisse. Nous pouvons également dire que chaque point sur la courbe d'une fonction vérifie que son ordonnée est égale à f de son abscisse. Pour vérifier si un point appartient à la courbe d'une fonction, nous devons simplement calculer f de son abscisse et voir si cela correspond à son ordonnée. Si oui, le point appartient à la courbe de la fonction. Sinon, il n'y appartient pas. Dans notre exemple, nous avons calculé g de moins 2 pour trouver que l'abscisse de a est bien égal à son ordonnée, donc le point a appartient à la courbe de g.

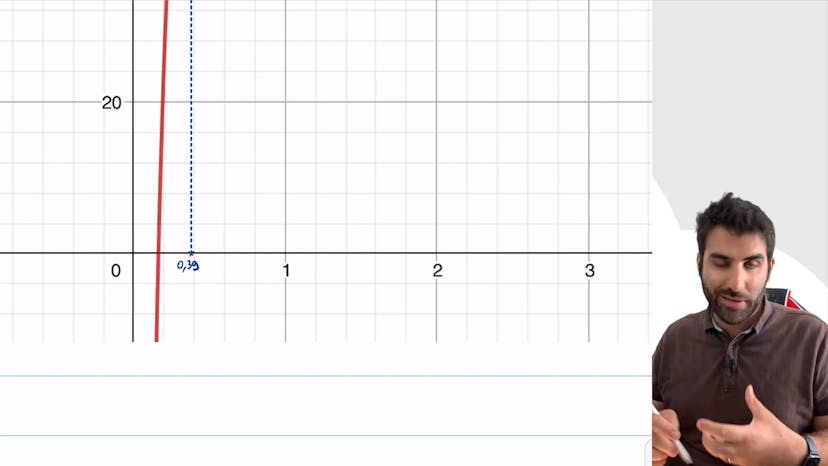
Résolution graphique : équation

L'exercice consiste à trouver graphiquement l'égalité entre f(x) et g(x) en tracant les courbes. Le point d'intersection des deux courbes est important car il donne l'abscisse du ou des points d'intersection, selon s'il y en a plusieurs. Pour résoudre graphiquement f(x) = g(x), il suffit de lire l'abscisse des points d'intersection. Dans cet exercice, le point d'intersection a une abscisse d'environ 0,39, il est donc possible de dire que f2x égale g2x a pour solution x est égal à 0,39. Il est important de noter que la précision n'est pas nécessaire, une approximation suffit.

Inéquation avec x²

Ce cours explique comment résoudre l'inéquation x² < 7 en utilisant la méthode générale pour résoudre une inéquation x² ≤ k ou x² ≥ k. Si k est négatif, il n'y a pas de solution pour x² < k car x² est toujours positif ou nul. Si k est positif, x² ≤ k a pour solution l'intervalle [−√k, √k) et x² > k a pour solution (−∞, −√k) ∪ (√k, ∞). Comme k = 7 est positif, l'inéquation x² < 7 a pour solution l'intervalle (−√7, √7).