 All subjects
All subjects
 All subjects
All subjects
Maths Expertes
Complexes
Terminale
test
Aucun résumé n'est disponible pour cette vidéo
Maths Expertes
Complexes
Terminale

Affixe, vecteurs et complexes
Le nombre complexe peut être associé à un point du plan, où l'on utilise la partie réelle et la partie imaginaire comme coordonnées. On peut également associer un vecteur à un nombre complexe, et inversement. Dans un exemple pratique, on utilise les affixes des points A, B, et C pour trouver le point D tel que ABCD soit un parallélogramme. On utilise la propriété qui dit que AB est égal à DC si et seulement si les affixes respectives de ces deux vecteurs sont égales. Cette méthode est équivalente à l'utilisation de vecteurs.
Maths Expertes
Complexes
Terminale

Forme trigo, Forme expo
Ce cours de maths porte sur l'écriture trigonométrique et exponentielle d'un nombre complexe. Il explique comment exprimer les coordonnées A et B avec le module de Z et l'angle θ. La forme trigonométrique est obtenue en remplaçant A et B par leurs équations en fonction de Z et θ. La forme exponentielle est une écriture compacte qui permet de simplifier certains calculs, elle est définie comme E de iθ égal à cosθ plus i sinθ. Cette quantité a des propriétés similaires à celles de l'exponentielle en maths réelles, ce qui justifie son appellation.
Maths Expertes
Complexes
Terminale

Racines de l'unité
Ce cours traite des racines énièmes de l'unité, qui sont des nombres complexes vérifiant Z^n = 1. On démontre que l'ensemble de ces racines a exactement n éléments en utilisant la formule E^(2iπk/n). Les racines de l'unité ont une intuition géométrique et peuvent aider à résoudre des équations complexes. Pour résoudre z^n = z0, où z0 est un nombre complexe avec un module et un argument, on utilise la formule z0^(1/n) * E^(iθ/n)^k, où k est compris entre 0 et n-1. Un exemple est donné et suivi d'un corrigé. L'accent est mis sur la compréhension de l'intuition géométrique et de l'application de la formule.
Maths Expertes
Complexes
Terminale

Savoir-faire : les médiatrices
En géométrie, un point peut être repéré soit par une abscisse et une ordonnée (coordonnées cartésiennes), soit par sa distance à l'origine et l'angle qu'il forme avec l'axe des abscisses (coordonnées polaires). En utilisant les nombres complexes, la norme du vecteur représentant un point correspond à son module, tandis que l'angle qu'il forme avec l'axe des abscisses correspond à son argument. Pour trouver l'ensemble des points à une distance donnée de l'origine, on trace un cercle, mais pour trouver un point spécifique, on combine la distance avec l'angle. La norme du vecteur entre deux points correspond à la distance entre ces points, et peut être définie comme la différence entre leurs nombres complexes associés. Cette propriété est utile pour identifier des droites médiatrices en utilisant des équations complexes. Pour trouver l'ensemble de points qui vérifie une relation donnée, il faut repérer les Z-ZA et Z-ZB correspondants et comprendre que cela correspond à une médiatrice.
Maths Expertes
Complexes
Terminale
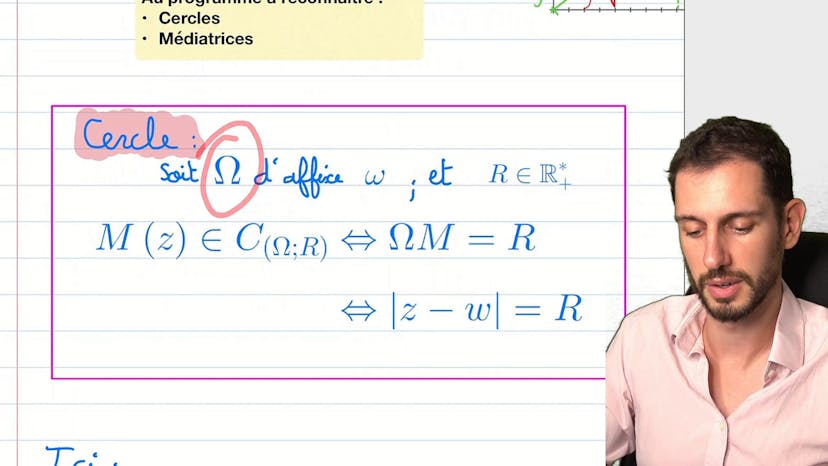
Savoir-faire : les cercles
Ce cours explique comment la représentation complexe peut être utilisée pour trouver des équations de cercles dans le plan. Un point peut être vu comme une intersection d'une abscisse et d'une ordonnée, mais il peut également être défini par sa distance à l'origine et son angle avec l'axe des abscisses. Pour définir un cercle, il faut que tous les points soient équidistants d'un point fixe. En utilisant la représentation complexe, cette distance peut être traduite en norme de la différence entre deux nombres complexes. Si une équation contient l'expression de la norme d'un nombre complexe égale à un nombre constant, alors cela peut être interprété comme une équation de cercle de centre et de rayon déterminés par les parties réelles et imaginaires du nombre complexe.
Maths Expertes
Complexes
Terminale

Forme expo 1 : méthode type
Le cours explique comment trouver la forme exponentielle de 2-2i en suivant une méthode classique de calcul, en factorisant Z et en trouvant son module. Le résultat est ensuite simplifié en utilisant les formules de trigonométrie pour identifier cosθ et isinθ. Finalement, la réponse est obtenue sous la forme exponentielle iθ. Une méthode plus astucieuse sera expliquée dans la vidéo suivante.
Maths Expertes
Complexes
Terminale

Forme expo 2 : + rapide
Dans cette vidéo, l'enseignant donne une méthode astucieuse pour résoudre les exercices de complexes en passant à travers les mailles du système. Il conseille d'apprendre les nombres complexes classiques, tels que π sur 6, π sur 4, π sur 3, en forme algébrique et en forme trigonométrique exponentielle dans les deux sens pour gagner du temps. Il montre ensuite comment utiliser cette méthode pour résoudre un exercice en reconnaissant que 2 - 2i est égal à 2 fois 1 - i et que 1 - i a une forme complexe connue. Enfin, il encourage les élèves à pratiquer la méthode classique au début, mais à passer rapidement aux astuces pour gagner du temps.
Maths Expertes
Complexes
Terminale
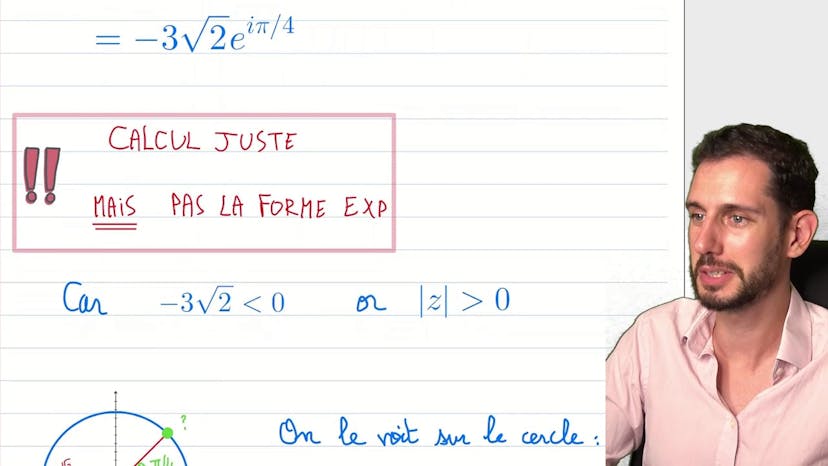
Forme expo 3 : erreur type !
Dans ce cours, nous apprenons comment éviter les erreurs lors de la résolution d'exercices de nombres complexes. Il est important de faire attention aux exercices piégeux, qui peuvent mettre en évidence une structure exponentielle. Dans l'exemple présenté, la forme exponentielle de (-3, -)3i doit être trouvée en utilisant l'astuce de connaître les nombres typiques couramment utilisés dans les exercices. Toutefois, il est crucial de noter que la forme exponentielle est égale à mod z fois e2iθ, avec θ représentant l'argument de z et que cela peut être différent de la solution obtenue. Pour résoudre ce problème, on peut remplacer le moins un par e2iπ pour trouver la véritable forme exponentielle. En comprenant cette astuce et en la mettant en pratique, nous pouvons éviter les erreurs et obtenir de meilleures notes lors des contrôles.
Maths Expertes
Complexes
Terminale
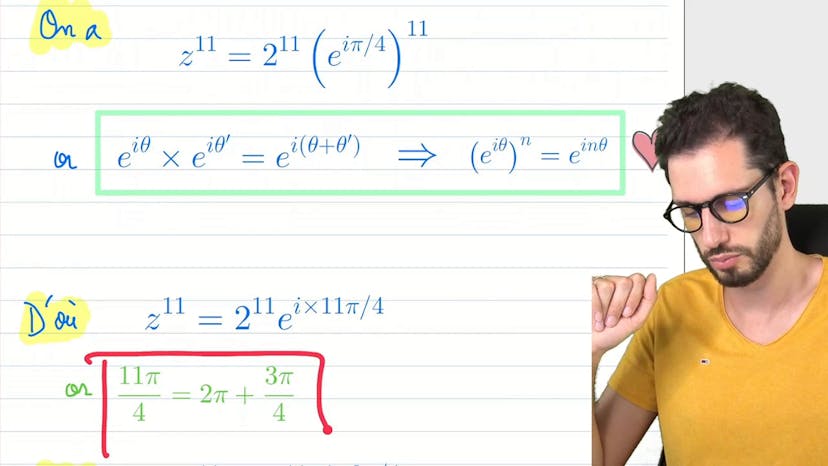
Forme expo → algébrique
Dans cette vidéo, on va utiliser la forme exponentielle pour obtenir une forme algébrique en travaillant avec la puissance 11 de z, où z est égal à 2EI pi sur 4. En utilisant des formules d'exponentielle complexe, on parvient à exprimer z puissance 11 sous la forme 2 puissance 10 fois racine de 2 fois moins 1 plus i. Pour cela, on cherche un angle simple en exprimant 11pi sur 4 en fonction de 2pi pour trouver les valeurs du cosinus et du sinus nécessaires pour la forme algébrique. En exploitant les propriétés de l'exponentielle, on peut facilement simplifier les calculs et obtenir une réponse claire.
Maths Expertes
Complexes
Terminale

Classique : trouver un cos
Dans ce cours, nous explorons l'utilisation des propriétés complexes pour faire de la trigonométrie poussée. Nous cherchons à exprimer cos(pi/12) sous deux formes distinctes : une forme algébrique et une forme exponentielle utilisant la fonction exponentielle. Pour ce faire, nous utilisons des valeurs d'angle connues, telles que pi/2, pi/3, pi/4 et pi/6, afin de réécrire pi/12 en termes de tiers et quarts ou sixièmes. Nous jouons ensuite sur les propriétés de multiplication de la fonction exponentielle pour simplifier l'expression de cos(pi/12) avec des nombres réels qui composent la partie réelle et imaginaire. En isolant la partie réelle et imaginaire, nous obtenons deux résultats pour le prix d'un, le cos et le sin et pouvons identifier l'expression algébrique : cos(pi/12) = racine(2) x (1 + racine(3)/4), qui peut également être exprimée sous la forme racine(2) x (1 + racine(6)/4).
Maths Expertes
Complexes
Terminale
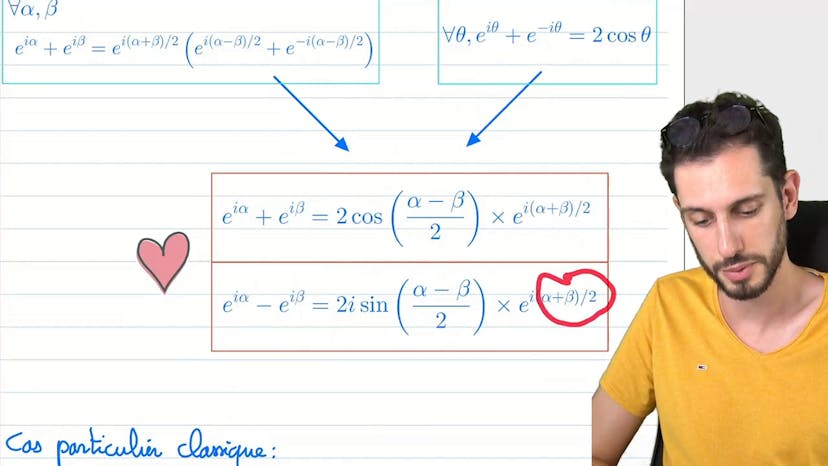
Astuce : angle moitié
This course teaches a method of factorizing and simplifying equations to make them easier to solve. The example given involves finding the exponential form of two complex numbers. The key is to factorize the equation by half angle to make it simpler, and then combine it with the formula for sum and difference. The resulting formula may or may not be in exponential form, depending on the sign of the cosine or sine. The course emphasizes the importance of understanding the formulas and being able to apply them to solve problems.


