Online Logarithme course by Top Instructors - Logarithme

Simplifier des expressions

Bienvenue dans ce cours sur les inéquations exponentielles et logarithmiques. Nous allons étudier les propriétés importantes pour résoudre ces équations. Pour la première équation ln(x) = 2, nous pouvons simplement composer avec l'exponentielle pour obtenir la solution x = e^2. Pour la deuxième équation e^x + 1 = 5, nous composons par le logarithme et trouvons x = ln(5) - 1. Pour la troisième équation 3ln(x) - 4 = 8, nous isolons le terme ln(x) avant de composer par l'exponentielle et obtenons x = e^(4/3). Pour les inéquations, nous devons toujours prendre en compte l'ensemble de définition. Par exemple, pour ln(6x - 1) > 2, nous composons par l'exponentielle pour obtenir la solution x > e^2 + 1/6. Pour e^x + 5 > 4e^x, nous rassemblons les termes exponentiels avant de composer par le logarithme et trouvons x < ln(5/3). Pour ln(x-3) + ln(9-x) = 0, nous combinons les termes ln pour obtenir ln((x-3)(9-x)) = 0, puis composons par l'exponentielle pour trouver les solutions x = 6 ± √8. Enfin, pour 3 - x > 0 et x + 1 > 0, nous résolvons l'inéquation ln(3-x)/(x+1) < 1 en multipliant par (x+1) et trouvons la solution x > 2. En résumé, il est important de prendre en compte l'ensemble de définition, de rassembler les termes en exponentiels ou en logarithmes et de composer par la fonction réciproque pour résoudre les équations et les inéquations exponentielles et logarithmiques.

Équations Inéquations

Dans ce cours, nous abordons une nouvelle inéquation avec le logarithme, similaire à celle que nous avons vue précédemment. L'équation proposée pour la résolution est 3-ln(2x+1)/2 > 1. Pour résoudre cette équation, nous voulons isoler le terme en ln afin de pouvoir composer par l'exponentielle et l'isoler. Comme d'habitude, il est important de vérifier l'ensemble de définition de l'inéquation avant de continuer. Dans ce cas, nous devons nous assurer que 2x+1 est strictement supérieur à 0. Cela signifie que nous devons résoudre l'inéquation sur l'intervalle -1/2 à l'infini. Pour isoler le terme en ln, nous déplaçons le facteur 3 de l'autre côté de l'inéquation, ce qui le transforme en -2. Ensuite, nous multiplions par -1 pour inverser le sens de l'inégalité. Maintenant, nous avons isolé parfaitement le ln. À ce stade, nous composons par l'exponentielle pour obtenir 2x+1 < e^4. Cette résolution est assez simple, nous isolons x pour obtenir x = e^4 - 1/2. Il est important de rappeler que l'intervalle sur lequel nous résolvons l'inéquation est -1/2 à l'infini. Nous devons vérifier si e^4 - 1/2 est compris dans cet intervalle. Comme cela est le cas, l'intervalle solution est l'intersection de ces deux intervalles, ce qui donne -1/2 à e^4 - 1/2. Il est crucial de ne pas oublier de vérifier l'ensemble de définition au début et de prendre l'intersection de la solution finale avec l'intervalle initial de résolution. Cette méthode nous permet d'isoler le terme en logarithme, de prendre l'exponentielle par la suite et de prendre en compte les intervalles de définition.

Exposant=Inconnue ?

Dans ce cours, on utilise l'exponentiel et le logarithme pour résoudre des inéquations où l'inconnu est un exposant. Cela est souvent utilisé en physique, notamment pour calculer la durée nécessaire pour que 80% des atomes radioactifs aient disparu. On utilise les lois géométriques, mais pour résoudre rigoureusement ces problèmes, on passe par la définition de l'exponentiel pour les puissances. Pour une puissance B non entière, on utilise la formule A^B = E^(B*ln(A)). Ainsi, lorsque l'inconnu est à l'exposant d'une puissance, on revient à la définition exponentielle. Dans l'exemple donné, 1/5^n est égal à E^(n*ln(1/5)) = E^(-n*ln(5)), ce qui est inférieur à 0,01. En isolant l'exponentielle, on obtient -n*ln(5) < ln(0,01). En multipliant par -1 et en divisant par ln(5), on obtient n > ln(0,01)/ln(5). En vérifiant la cohérence de nos calculs, on constate que pour des valeurs de n suffisamment grandes, la suite géométrique tend vers 0, ce qui confirme notre résultat. Dans un autre exemple, avec 1,22^n > 10^5, on utilise également la notation exponentielle pour obtenir E^(n*ln(1,22)) > E^(5*ln(10)). On en déduit n > 5*ln(10)/ln(1,22). En vérifiant la cohérence, on confirme que notre résultat est correct. En conclusion, il est important de revenir à la définition de la puissance avec l'exponentiel et le logarithme pour résoudre ces types de problèmes. N'hésitez pas à consulter la FAQ en cas de questions.

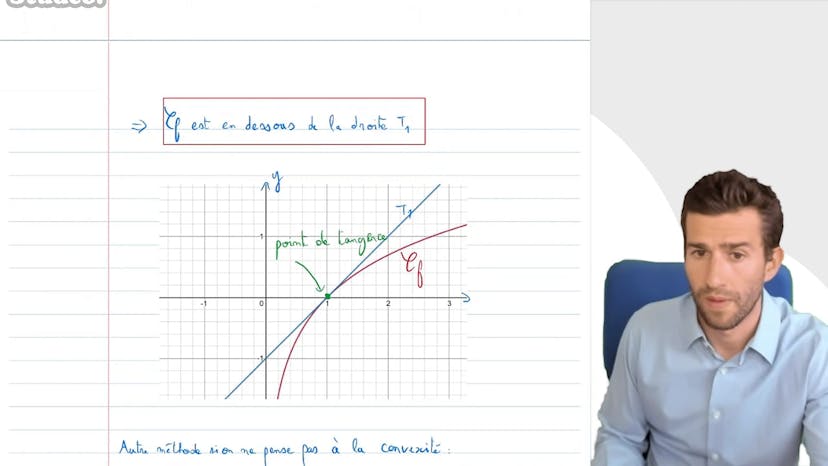
Courbe et Tangentes

Dans ce cours, nous étudions la fonction logarithme et cherchons à trouver l'équation de la tangente au point d'abscisse 1. Pour cela, nous utilisons la dérivée de la fonction logarithme, qui est égale à 1/x. En évaluant cette dérivée au point d'abscisse 1, nous obtenons une tangente d'équation y = x - 1. Ensuite, nous nous intéressons à la position relative de la courbe par rapport à sa tangente. Nous pouvons étudier cette position en examinant la convexité de la fonction. En calculant la dérivée seconde de la fonction logarithme, qui est égale à 1/x², nous constatons que la fonction est concave. La courbe se trouve donc en dessous de toutes ses tangentes, y compris celle au point d'abscisse 1. Nous pouvons également utiliser une méthode alternative en effectuant une étude de fonction classique. Pour cela, nous créons une fonction auxiliaire, g(x) = ln(x) - x + 1, et étudions le signe de cette fonction en examinant ses variations. En dérivant g(x), nous trouvons que cette dérivée est positive pour x compris entre 0 et 1, et négative pour x supérieur à 1. Ainsi, nous obtenons le tableau de variation de g(x), qui montre que g(x) est inférieur à 0 pour tout x, ce qui signifie que la différence entre la courbe et la tangente est toujours négative ou nulle. En conclusion, nous avons déterminé que la tangente au point d'abscisse 1 de la fonction logarithme a pour équation y = x - 1, et que la courbe de la fonction logarithme est en dessous de cette tangente. Cette méthode permet de reconnaître facilement cette tangente et de l'utiliser dans des calculs ultérieurs. Il est également recommandé de penser à la concavité pour déterminer la position relative de la courbe par rapport à sa tangente.

Dérivabilité et Variations

Cet article traite de l'étude d'une fonction logarithmique, qui est facile à étudier mais utilise une méthode classique. La fonction proposée est ln2x+1/ln2x-1, définie sur 0 exclu jusqu'à l'infini. La méthode utilisée pour étudier cette fonction est de la dériver, en utilisant la formule g' = u'v - uv' / v², ce qui permet d'obtenir une fonction dérivée de la forme -2x / (ln2x - 1)², qui est strictement négative sur 0e, mais aussi sur e jusqu'à l'infini, sauf en e où elle est indéfinie. Le tableau des variations de la fonction est ensuite déterminé en calculant les limites de la fonction en 0, e-, e+ et à plus l'infini, pour avoir un tableau des variations complet. Il est également noté que la présence de la valeur interdite du logarithme engendre une asymptote verticale en x = e et une asymptote horizontale en y = 1. Enfin, il est souligné que la fonction n'est pas strictement décroissante sur tout l'intervalle.

Croissance Comparée

Dans ce cours, nous analysons la fonction f qui définit la position suivante 3-x + 2ln2x. Nous dérivons la fonction pour trouver son signe et en déduire que la fonction est décroissante sur R étoile plus. En utilisant des croissances comparables, nous trouvons les limites de la fonction à l'infini et à 0. Nous utilisons ces limites pour établir le tableau de variation de f et trouver son extrémum. Ensuite, nous étudions la convexité de f en trouvant la dérivée seconde et en déduisant qu'elle est concave sur R étoile plus tout entier.

Ln : Limites

Nous allons voir comment calculer des limites qui font intervenir la fonction ln. Pour cela, nous allons utiliser le principe de factorisation du terme prédominant et nous allons essayer de nous ramener à des limites usuelles en utilisant les propriétés sur le logarithme.Pour la première limite, nous avons 2 ln(x²) - 5 ln(x) + 1. En factorisant par le terme prédominant ln(x²), nous obtenons 2 - 5/ln(x) + 1/ln²(x), qui tendent toutes vers 0, donc la limite est plus l'infini.Pour la deuxième limite, qui est du ln(√x)/ln(2x), qui tend vers l'infini, nous utilisons les propriétés sur le logarithme pour transformer √x en x^(1.5) et obtenir 1.5 ln(x)/ln(2) + ln(x)/ln(2). En factorisant par le terme prédominant ln(x), nous obtenons 1.5 + ln(2)/ln(x), qui tend vers 1.5.Enfin, pour la dernière limite, qui est (x-1)² ln(x-1) quand x tend vers 1, nous posons grand x = x-1 pour obtenir x² ln(x). En séparant le x, nous obtenons x * x ln(x), qui tend vers 0, donc la limite recherchée est égale à 0.Si vous avez des questions, n'hésitez pas à consulter la FAQ.

Dériver ln(u)

Ce cours aborde la méthode pour déterminer l'ensemble de définition d'une fonction avec logarithme et calculer sa dérivée. Il est important de bien regarder l'ensemble de définition d'une expression, notamment pour une inégalité. La première fonction est f(x) = ln(8x-4), pour laquelle l'ensemble de définition est 1/2 à l'infini et la dérivée est 2/(2x-1). La deuxième fonction est f(x) = ln(x^2 + x + 1), qui est définie et dérivable sur R tout entier et la dérivée est 2x/(x^2 + x + 1). La troisième fonction est f(x) = ln(u/v), avec u(x) = x-1 et v(x) = 2x+4. L'ensemble de définition est (-∞, -2) U (1, +∞) et la dérivée est (6/(v(u-v))(u/v)). Finalement, la quatrième fonction est f(x) = ln(e^x / e^0.1x), qui est définie et dérivable sur R+ étoile et la dérivée est e^x / e^0.1x. Il est important de mémoriser de toujours vérifier l'ensemble de définition pour une expression impliquant une fonction logarithmique.

Déf fondamentale

Le logarithme, noté ln, est une fonction définie sur l'intervalle des nombres réels strictement positifs. Pour un nombre réel x strictement positif, ln(x) est l'unique solution de l'équation 2y = x. On peut définir le logarithme avec n'importe quel nombre x, en appelant la solution de l'équation 2y = x, ln(x). Les fonctions exponentielle et logarithme sont réciproques l'une de l'autre, ce qui signifie que la fonction exponentielle de ln(x) est égale à x, et que ln de la fonction exponentielle de x est égale à x. Cependant, ces fonctions ne sont pas définies de la même manière pour tous les x. Par exemple, le logarithme n'est défini que pour les x positifs stricts. Il est important de se rappeler que la racine carrée d'un carré est égale à la valeur absolue du nombre d'origine, et que la fonction logarithme et la fonction exponentielle sont réciproques l'une de l'autre.

On redécouvre le log ?!

Le cours porte sur la fonction LN et sa relation fonctionnelle. Il s'agit de déterminer les fonctions satisfaisant l'équation f2ab = f2a + f2b et f'(1) = 1. En utilisant la dérivée du log, on démontre que si la fonction est non nulle et définie en 0, alors elle est égale à zéro partout. On conclut donc que la fonction ne peut pas être définie en 0. Ensuite, on démontre que f(1) = 0 en utilisant la relation fonctionnelle. On établit également que f(x/y) = f(x) - f(y) en s'inspirant de la démonstration de log(a/b) = log(a) - log(b). Enfin, on détermine le sens de variation de f sur (0, +∞) en utilisant la dérivée f'(x) = 1/x. On conclut en disant qu'en partant de ces deux propriétés, on peut retrouver toutes les propriétés du log et définir fondamentalement la fonction LN.

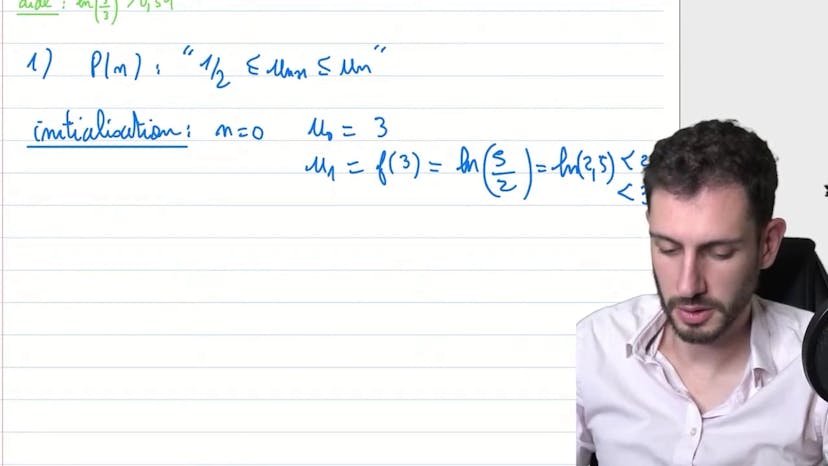
Fonction et suite récurrente associée

Dans ce cours, nous étudions une fonction définie par une fraction rationnelle avec un degré de 1 au-dessus et en-dessous de la barre de fraction. La fonction est définie sur l'intervalle de 0 à l'infini. Nous déterminons la limite de la fonction lorsque x tend vers l'infini et interprétons graphiquement cette limite comme un plateau atteint par la fonction à mesure que x tend vers l'infini. Ensuite, nous démontrons que la dérivée de la fonction est égale à une expression donnée pour tout nombre réel positif ou nul. Nous utilisons des transformations mathématiques pour simplifier le calcul de la dérivée. Nous concluons en disant que la fonction est strictement croissante et positif sur son ensemble de définition. Dans la deuxième partie du cours, nous étudions une suite définie par récurrence à l'aide de la fonction précédemment étudiée. Nous démontrons par récurrence que la suite est décroissante et minorée. Nous utilisons des calculs numériques pour vérifier l'initialisation de la récurrence et la propriété héréditaire. Enfin, nous concluons en disant que la suite converge vers une limite strictement positive en utilisant le théorème des suites décroissantes et minorées.