Online Learning Courses

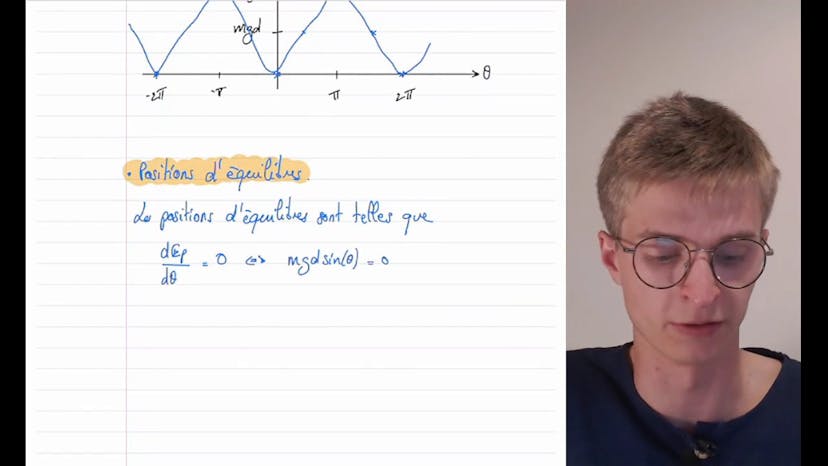
Energie mécanique du pendule pesant

Dans cette vidéo, Théobald de Studio nous parle du pendule pesant et de son énergie mécanique. Il commence par décrire les différentes caractéristiques du pendule, telles que le moment d'inertie (J), le centre de gravité (G) et la distance entre G et l'axe des zéros (D). Il énonce ensuite les questions qui seront traitées dans l'exercice. La première question concerne l'énergie cinétique du pendule. Théobald explique que l'énergie cinétique d'un solide en rotation autour d'un axe fixe est égale à 1,5 de Jθ², où θ est l'angle de rotation du pendule. Ensuite, il aborde l'énergie potentielle du pendule. Il explique que cette énergie est égale à mgd(1-cosθ), où m est la masse du pendule, g est l'accélération due à la gravité, d est la distance entre G et l'axe des x, et θ est l'angle de rotation. Théobald explique alors pourquoi l'énergie mécanique du pendule est constante au cours du mouvement. Il explique que cela est dû au fait que les seules forces agissant sur le pendule sont le poids (une force conservative) et l'action de la liaison pivot (qui ne travaille pas). Par conséquent, l'énergie mécanique est une intégrale première du mouvement. La troisième question porte sur l'équation différentielle du mouvement du pendule. Théobald montre comment dériver l'expression de l'énergie mécanique par rapport à θ pour obtenir cette équation du mouvement. Ensuite, il explique comment tracer le profil d'énergie potentielle du pendule et comment trouver les positions d'équilibre. Il montre que ces positions d'équilibre sont stables lorsque la dérivée de l'énergie potentielle par rapport à θ est positive, et instables lorsque cette dérivée est négative. Il discute ensuite des deux comportements possibles du pendule. Si l'énergie mécanique est inférieure à 2mgd, le pendule oscille entre deux positions extrêmes et a un comportement pendulaire. Si l'énergie mécanique est supérieure à 2mgd, le pendule peut prendre toutes les valeurs d'énergie potentielle et effectuer des tours complets, ce qui correspond à un comportement révolutif. En conclusion, Théobald souligne l'importance de bien comprendre tous les concepts abordés dans cet exercice, car ils sont récurrents et utiles dans le domaine du pendule pesant. Il encourage les spectateurs à poser des questions et annonce une prochaine vidéo à venir.

Saut de Tarzan

Dans cette vidéo, on étudie le mouvement de Tarzan se déplaçant le long d'une liane. Tarzan est assimilé à un point matériel de masse 70 kg. La liane est de longueur 10 mètres et de masse négligeable, accrochée à un point fixe O. Lorsqu'il attrape la liane, celle-ci forme un angle de 30 degrés avec la verticale. On néglige les frottements et la masse de la liane. La première question est de justifier l'utilisation des coordonnées polaires. Le mouvement s'effectue dans le plan vertical, car les forces appliquées sur Tarzan (son poids et la tension de la liane) sont verticales. De plus, le mouvement démarre avec une vitesse nulle, ce qui confirme que le mouvement se déroule dans le plan vertical. Étant donné que le mouvement est à la fois vertical et circulaire, on peut utiliser des coordonnées polaires. La deuxième question consiste à utiliser le théorème de l'énergie cinétique pour obtenir l'équation du mouvement. L'énergie cinétique du système est égale à 1/2 * masse * (longueur de la liane)^2 * (dérivée de l'angle theta par rapport au temps)^2. Les puissances des forces appliquées (poids et tension de la liane) sont calculées. En dérivant l'énergie cinétique par rapport au temps, on obtient l'équation du mouvement : (dérivée seconde de l'angle theta par rapport au temps) + (gravité * sinus de l'angle theta / longueur de la liane) = 0. La dernière question est de déterminer la tension s'exerçant sur Tarzan lorsque la liane forme un angle theta avec la verticale. On applique le principe fondamental de la dynamique : la masse fois l'accélération est égale à la somme des forces (poids et tension de la liane). En projetant cette équation sur le vecteur unitaire UR, on obtient une expression pour la tension en fonction de la masse, de la gravité, de l'angle theta et de l'angle alpha (angle lorsque Tarzan attrape la liane) : tension = 3 * masse * gravité * cos(theta) - 2 * masse * gravité * cos(alpha). Cet exercice est important pour comprendre le mouvement de Tarzan le long de la liane. La deuxième partie, où l'on cherche à déterminer la tension, est particulièrement significative. Si vous avez des questions, n'hésitez pas à les poser en commentaire.

Etude de manège

Dans cette vidéo, Oval2Studio aborde les questions suivantes concernant un manège : 1. Est-il possible de considérer un manège comme un solide indéformable ? 2. À quelles conditions les enfants peuvent-ils être inclus dans le modèle du solide indéformable ? 3. Un enfant peut-il être en translation circulaire sur un manège ? 4. Comment exprimer la vitesse d'un enfant assis sur un cheval sur le manège ? Un solide indéformable est un solide dont les points restent à une distance constante les uns des autres. Un manège vide peut être considéré comme un solide indéformable, mais la présence d'éléments mobiles tels que des chevaux peut rendre cette considération non valable. Pour inclure les enfants dans le modèle du solide indéformable, ils doivent être solidement attachés et complètement immobiles. Un enfant assis sur un manège n'est pas en translation circulaire car ses mains n'effectuent pas un mouvement circulaire avec le même rayon. Cependant, si l'enfant est assimilé à un point matériel, il est en translation circulaire. Pour calculer la vitesse de l'enfant, on le considère comme un point matériel situé à une distance de 2 mètres du centre du manège. La vitesse de rotation du manège est de 2π/24 radian par seconde. La vitesse de l'enfant est donc de 0,52 mètre par seconde. En conclusion, cet exercice démontre que la vitesse de l'enfant sur le manège dépend de sa position par rapport au centre du manège. Ce résumé SEO friendly couvre les principales questions et réponses de la vidéo d'Oval2Studio sur le manège.

Pendule à deux masses

Dans cette vidéo, nous étudions un pendule à deux masses. Le pendule est composé d'une tige rigide de longueur L, avec deux masses identiques de masse m fixées à une distance de L/2 et une distance L du centre O. Nous négligeons le moment d'inertie de la tige. Dans la première question, nous devons montrer que l'équation du mouvement s'écrit comme suit. Pour ce faire, nous utilisons le théorème du moment cinétique et appliquons la loi scalaire du moment cinétique par rapport à l'axe de rotation, donnant dLoz/dt = somme des moments des forces. Nous calculons les moments des forces exercées sur les masses (les poids P1 et P2) et obtenons l'équation du mouvement θ¨ + (6GM/5L)sinθ = 0. Dans la deuxième question, nous devons montrer que le centre de masse G du système se trouve à une distance de 3L/4 du centre O. En utilisant la définition du centre de masse, nous trouvons que OG = (3L/4)UR, confirmant que G est à une distance de 3L/4 de O. Dans la troisième question, nous devons déterminer si l'étude précédente est équivalente à celle d'un système où seule une masse de 2M est située en G. En appliquant la loi scalaire du moment cinétique à ce nouveau système, nous obtenons une équation du mouvement différente θ¨ + (4GM/3L)sinθ = 0. Par conséquent, les deux systèmes ne sont pas équivalents car ils ont des équations du mouvement différentes. Il est important de noter que la dynamique d'un solide en rotation n'est pas simplement donnée par la dynamique d'un point matériel en son centre d'inertie. Cette équivalence n'est valable que pour un solide en translation. Les deux systèmes étudiés dans cette vidéo sont donc distincts et donnent des équations du mouvement différentes.

Machine tournante et volant d'inertie

Dans cette vidéo, nous nous intéressons à une machine tournante équipée d'un volant d'inertie. Le volant d'inertie est un anneau de masse et de rayon ajouté à la machine tournante. Il permet de réguler la vitesse angulaire de rotation de la machine. On considère une machine tournante dont la vitesse angulaire de rotation est régulée par un volant d'inertie. Le volant d'inertie est un anneau lié au rotor, de masse élevée et de grand rayon. La machine tournante est modélisée par un moment d'inertie J et est soumise à un couple moteur constant γ0 et un couple de frottement fluide γf, égal à moins αω, où α est un certain coefficient positif. La première question demande de justifier, en utilisant un argument énergétique, que α est supérieur à 0. En regardant la puissance du couple de frottement, on constate qu'elle doit être négative. Pour que cela soit possible, α doit être positif dans l'équation. Donc, α est supérieur à 0. La deuxième question demande de trouver l'évolution de la vitesse angulaire ω en fonction du temps. On introduit la vitesse finale ωf et un temps caractéristique τ. En résolvant l'équation différentielle, on obtient que ω en fonction du temps est égal à ωf(1 - exp(-t/τ)). Ensuite, on introduit un couple de vibrations γvib égal à γcos(ωt) et on se demande pourquoi on ne perd pas en généralité en considérant ce couple. L'équation différentielle étant linéaire, on peut reconstruire la réponse à n'importe quelle forme de vibration grâce au théorème de Fourier. Ainsi, en ajoutant ce couple de vibrations, on rajoute simplement une contrainte supplémentaire au système, mais cela n'affecte pas la résolution de l'exercice. En considérant ce nouveau couple de vibrations, on cherche à déterminer le temps caractéristique de la durée du régime transitoire. Ce couple de vibrations ne dépend pas de ω et n'affecte pas le régime transitoire, qui est toujours caractérisé par τ, égal à J/α. Enfin, on cherche la vitesse angulaire de rotation après le régime transitoire, sous la forme ω = ωf + Acos(ωt + φ) et on nous demande de déterminer l'amplitude A. L'équation différentielle devient J(dω/dt) + γ0 - αω + γcos(ωt). En utilisant le principe de superposition, on trouve que A = γ/√(α² + Jω²). En conclusion, l'avantage d'un volant d'inertie est qu'il permet de stabiliser la vitesse angulaire d'une machine tournante en diminuant l'impact des variations et des vibrations. Cependant, son inconvénient est qu'il augmente la durée du régime transitoire, ce qui retardera l'atteinte du régime permanent.

Tableau suspendu

Dans cette vidéo, Théobaldo Studio étudie le mouvement d'un tableau accroché au mur qui effectue de petites oscillations autour de sa position d'équilibre. Le tableau est rectangulaire, de masse m, et oscille autour de l'axe delta perpendiculaire au mur. Le moment d'inertie du tableau par rapport à cet axe est donné par J = m(A^2 + 4B^2/12). La position du tableau est repérée par l'angle theta entre OG et la verticale passant par O. Dans la première question, il faut trouver l'équation du mouvement. En appliquant le théorème du moment cinétique par rapport à delta, on trouve que J * theta point point + MgB/2 sin(theta) = 0. En simplifiant l'expression dans le cadre des petites oscillations, où sin(theta) peut être approximé à theta, on obtient l'équation d'un oscillateur harmonique : theta point point + (MgB/2J) * theta = 0. La période de ces oscillations est donnée par T = 2π * racine(J/(MgB/2)). Dans la troisième question, si la surface du tableau reste constante et que A est augmenté, la période augmentera si A > 2√3B et diminuera sinon. Dans la quatrième question, si B est augmenté, la période augmentera si B > √3/2A. Cet exercice nécessite des calculs et des études de fonctions.

Volume dans une seringue

Dans cette vidéo, nous abordons le chapitre des fondements de la thermodynamique. Nous commençons par examiner le cas d'une seringue dans laquelle nous comprimons l'air avec un piston. Au départ, la pression est égale à la pression atmosphérique, soit 1 bar. L'air est considéré comme un gaz parfait à température constante. Le problème consiste à déterminer la pression finale lorsque le volume est réduit de 90%. Pour résoudre ce problème, nous devons choisir le système sur lequel appliquer les théorèmes de la thermodynamique. Dans ce cas, le système est l'air à l'intérieur de la seringue, avec une pression initiale de V1, un volume de V1, une température de T, et une quantité de matière Na. Nous pouvons utiliser l'équation d'un gaz parfait, P1V1 = NaRT, pour lier ces variables d'état. En réduisant le volume de 90%, nous posons un défi pour déterminer les nouvelles variables d'état, P2, V2, T et Na. Comme la transformation est à température constante et qu'il n'y a pas de fuite d'air, T et Na restent les mêmes que dans l'état initial. En utilisant de nouveau l'équation d'état du gaz parfait, P2V2 = NaRT, nous pouvons résoudre le problème. En utilisant les deux équations d'état, nous trouvons que P2V2 = P1V1, et en supposant que V2 = 0,1V1, nous pouvons conclure que P2 = 10P1. En effectuant le calcul, nous obtenons une pression finale de 10 bars pour cette transformation. Dans la deuxième question, nous cherchons à obtenir une pression de 2,5 bars. En utilisant à nouveau l'équation P2V2 = P1V1, nous trouvons que le rapport V2/V1 est égal à P1/P2. Nous pouvons alors déduire que pour obtenir une pression finale de 2,5 bars, le volume doit être réduit de 60%. En concluant, nous pouvons constater que l'utilisation de l'équation d'état du gaz parfait nous permet de résoudre ces problèmes thermodynamiques. En fixant les valeurs de Na, R et T, nous pouvons observer que la pression varie inversement avec le volume. Cette méthodologie nous permet de résoudre ces problèmes plus facilement. Merci d'avoir suivi cette vidéo et à bientôt !

Pression de pneus

Bonjour à tous ! Aujourd'hui, nous allons parler de la pression des pneus. La pression recommandée pour les roues avant d'une voiture est de 2,2 bars. Dans cet exercice, nous nous intéressons à la variation de pression en fonction de la température. Nous supposons que le volume des pneus ne change pas et qu'il n'y a aucune fuite d'air possible. Nous devons déterminer l'indication du manomètre lorsqu'il fait 30 degrés. Pour cela, nous utilisons l'équation d'état d'un gaz parfait, qui relie la pression, le volume, la température et la quantité de matière. Nous avons P1V = NAR T1. En isolant P1 / T1, nous obtenons P1 / T1 = NA R / V. Ensuite, nous déclarons un nouvel état final, avec une pression P2, un volume V, une température T2 et une quantité de matière NA. En utilisant à nouveau l'équation d'état des gaz parfaits, nous avons P2V = NAR T2. En isolant P2 / T2, nous obtenons P2 / T2 = P1 / T1. Nous cherchons maintenant la pression finale, l'indication du manomètre, qui est donnée par P2 = P1 * T2 / T1. En effectuant les calculs, nous obtenons une pression P2 de 1,9 bars. Ensuite, nous devons calculer la variation relative de pression due au changement de température. La variation relative de pression est donnée par (P2 - P1) / P1. En effectuant les calculs, nous obtenons une variation de 14%. En conclusion, pour compenser la perte de pression due aux variations de température, il est conseillé de légèrement augmenter la pression des pneus entre chaque saison. Cela permet de maintenir une pression standard pour une conduite optimale. Merci d'avoir suivi cet exercice sur la thermodynamique et à bientôt !

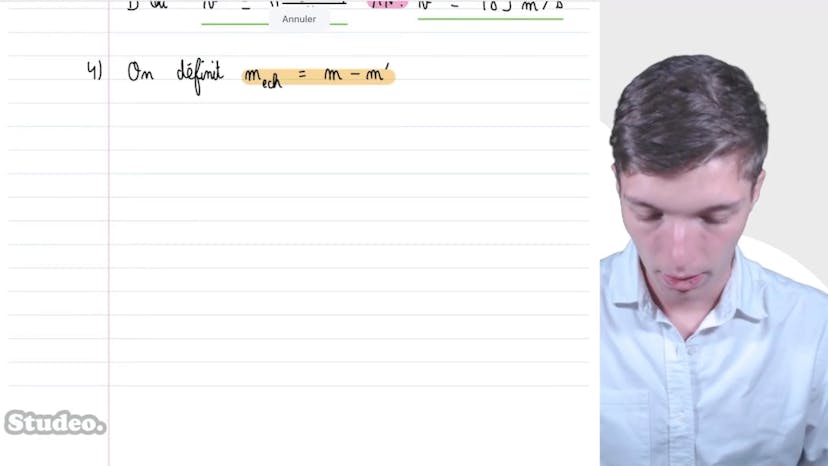
Helium

Dans cette vidéo, Matisse de Studio parle de l'hélium contenu dans une bouteille de volume constant (10 litres) à une pression de 2,1 bar et une température de 300 Kelvin. Il utilise l'équation d'état des gaz parfaits pour calculer la masse d'hélium dans la bouteille, qui est de 3,4 g. Il explique également comment calculer la densité particulière, qui est le nombre d'atomes par unité de volume, en utilisant l'équation d'état des gaz parfaits. La valeur obtenue est de 84 mol/m³. Il aborde ensuite la vitesse quadratique moyenne des atomes, qui correspond à la norme de la vitesse moyenne des molécules dans une pièce. La vitesse quadratique moyenne est calculée à l'aide de l'énergie cinétique moyenne, qui est égale à 1,5 fois la masse molaire fois la vitesse quadratique moyenne au carré. En utilisant des valeurs numériques, la vitesse quadratique moyenne est de 789 m/s. Ensuite, il analyse le cas où la pression passe à 1,4 bar et la température à 290 Kelvin après avoir ouvert la bouteille, ce qui entraîne une fuite de gaz. Il détermine la masse de gaz échappée en utilisant les nouvelles valeurs de pression et de température. La masse de gaz échappée est de 1,1 g d'hélium. Enfin, il explique comment déterminer la température nécessaire pour que la bouteille retrouve sa pression d'origine. Il utilise l'équation des gaz parfaits avec la quantité de matière restante dans la bouteille. La température calculée est de 450 Kelvin. En conclusion, Matisse souligne l'intérêt de cet exercice qui permet de comprendre les équations d'état des gaz parfaits et les variables importantes d'un système. Il encourage les spectateurs à revoir l'exercice de leur côté.

Pot de confiture

Dans cette vidéo, Matisse de Studio parle de l'utilisation d'un pot de confiture. Il explique que pour remplir le pot, on verse de la confiture à une température de 105°C et à une pression atmosphérique de 1 bar. Le pot a un diamètre de 82 mm et on laisse un espace entre la confiture et le bord du pot. L'air emprisonné entre le couvercle et la confiture est considéré comme un gaz parfait à une température T1. Le pot de confiture refroidit lentement jusqu'à atteindre une température de 20°C, et on souhaite déterminer la pression P2 à l'intérieur du pot à ce moment-là. Pour résoudre ce problème, Matisse applique la méthode classique de résolution thermodynamique. Il considère l'air à l'intérieur du pot comme le système et utilise l'équation d'état d'un gaz parfait (P1V = NAR T1) pour établir une relation entre la pression initiale (P1) et la température initiale (T1), et la pression finale (P2) et la température finale (T2). Il trouve finalement que la pression P2 est égale à 0,78 bar. Ensuite, Matisse aborde la seconde question qui consiste à déterminer la résultante des forces de pression sur le couvercle du pot une fois qu'il est refroidi. Il explique que pour relier la pression aux forces de pression, il faut connaître la définition de la force de pression. La force de pression sur une surface est donnée par P fois la surface fois la normale sortante de la surface. En prenant en compte la pression intérieure et la pression extérieure, Matisse trouve que la force sur le couvercle est égale à la valeur absolue de la différence entre la pression intérieure et la pression extérieure, multipliée par la surface du couvercle. En effectuant les calculs numériques, il obtient une force de 1,2 10-3 N due à cette différence de pression. Matisse explique que cela rendra plus difficile l'ouverture du pot, car la pression intérieure est inférieure à la pression extérieure. Il souligne que cela est dû aux forces de pression et à la sous-pression à l'intérieur du pot. Ces forces peuvent rendre encore plus difficile l'ouverture si le pot est sous vide. Il conclut en encourageant les spectateurs à comprendre pourquoi il est plus difficile d'ouvrir un pot en se basant sur la formule PxS (force de pression = pression fois surface) et en faisant des schémas pour mieux visualiser les concepts. En résumé, cette vidéo explique comment remplir un pot de confiture, comment calculer la pression à l'intérieur du pot une fois qu'il est refroidi, et comment les forces de pression affectent l'ouverture du couvercle du pot.

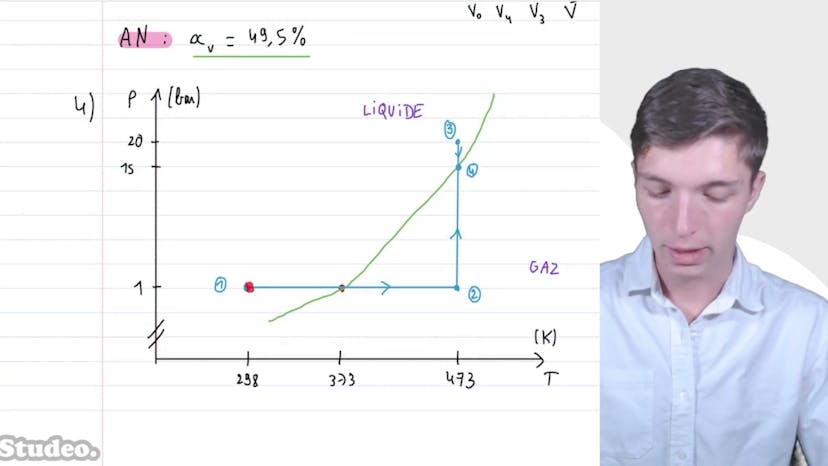
Diagramme (P,T)

Dans cette vidéo, nous étudions le diagramme pression-température de l'eau. Nous considérons une masse de 900 g d'eau à la température T1 de 298 Kelvin et à la pression de 1 bar. L'eau subit ensuite un chauffage à pression constante jusqu'à la température T2 de 473 Kelvin, puis une compression à température constante jusqu'à un volume de 100 litres, et enfin une détente à température constante jusqu'à un état d'équilibre liquide-vapeur de volume V4 de 50 litres. Nous tenons compte de la pression à vapeur saturante pour deux températures différentes, de la masse molaire de l'eau et de la constante des gaz parfaits. Dans l'état 1, nous n'avons pas la pression de vapeur saturante, mais la pression correspond presque à la pression de vapeur saturante pour 373 Kelvin. Cela indique que nous sommes dans un état liquide à 298 Kelvin et dans un état gazeux à 473 Kelvin. Pour l'état 2, qui correspond à l'état gazeux, nous pouvons utiliser l'équation d'état des gaz parfaits pour déterminer sa pression. En appliquant cette équation avec une masse de 900 grammes et la masse molaire de l'eau donnée, nous trouvons une pression de 20 bars. Nous pouvons alors comparer cette pression à la pression de vapeur saturante et conclure que l'état est liquide. Pour déterminer le titre en vapeur d'eau dans l'état 4, qui est un mélange liquide-gaz, nous utilisons le théorème des moments. En appliquant ce théorème, nous trouvons un titre en vapeur de 49,5%. Enfin, nous représentons les différentes transformations dans un diagramme pression-température, en passant d'une pression de 1 bar à 298 Kelvin à une pression de 20 bars à 473 Kelvin, avant de revenir sur la courbe de saturation pour le mélange liquide-gaz. En résumé, cette vidéo explore différentes transformations de l'eau dans un diagramme pression-température. Elle aborde des concepts tels que la pression de vapeur saturante, l'équation d'état des gaz parfaits, le titre en vapeur d'eau et le théorème des moments. N'hésitez pas à revoir cet exercice pour mieux comprendre ces concepts. Merci de nous avoir suivi et à bientôt !