 All subjects
All subjects
 All subjects
All subjects
Physique-Chimie
Physique
Terminale

Différence de marche
Dans cette vidéo, Matisse de Studio explique l'importance de la différence de marche en interférence. Il donne un exemple concret de deux vibreurs synchrones produisant des ondes à la surface d'un liquide et demande de déterminer la longueur d'onde des ondes produites pour chacun des vibreurs. Il explique ensuite comment exprimer la différence de marche entre les deux ondes en fonction de la distance B du vibreur V1 et précise la relation entre la différence de chemin et la longueur d'onde pour des interférences qui sont constructives.Matisse de Studio énumère ensuite les valeurs de B pour lesquelles l'amplitude des ondes au point P est maximale et calcule le nombre de franges d'interférences d'amplitude maximale entre les deux vibreurs. Au final, il y a 17 franges d'interférence constructive entre les deux vibreurs.Cet exercice permet de travailler les relations classiques et les manières de raisonner typiques du chapitre sur les interférences.
Physique-Chimie
Physique
Terminale
Diffraction
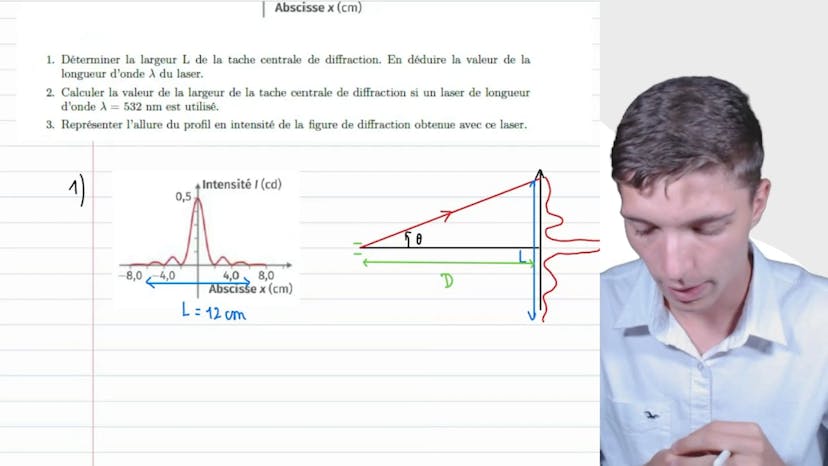
Dans cette vidéo, on explore le phénomène de diffraction en utilisant un laser rouge et une fente verticale de 35 micromètres. En analysant le profil en intensité de la figure de diffraction, on détermine la largeur de la tâche centrale de diffraction pour en déduire la longueur d'onde lambda du laser. On utilise une relation géométrique pour relier la tâche centrale de diffraction à l'angle de diffraction θ, qui est à son tour relié à la relation classique sin θ = λ/a. Ensuite, on utilise une application numérique pour obtenir la valeur de lambda qui est égal à 1,9 µm. Enfin, on calcule la valeur de la tâche centrale de diffraction pour un laser de longueur d'onde différente et on obtient une tâche beaucoup plus petite avec un profil de densité plus serré. L'exercice permet de comprendre l'importance d'identifier la relation géométrique et la relation classique pour obtenir les valeurs des grandeurs qui nous intéressent.
Physique-Chimie
Physique
Terminale

Enceintes
Dans cette vidéo, on apprend que les enceintes sont constituées d'un caisson avec un haut-parleur et une ouverture de diamètre d. On calcule la longueur d'onde des ondes sonores de fréquences 200 Hz, 2 Hz et 20 kHz en utilisant la relation classique ondulatoire. On déduit que les sons avec la longueur d'onde la plus grande seront les mieux diffractés. Une personne placée sur le côté de l'enceinte percevra mieux les sons graves car la longueur d'onde est inversement proportionnelle à la fréquence. Les enceintes comportent au minimum deux haut-parleurs, le woofer et le tweeter, avec des diamètres différents car le tweeter transmet principalement les sons aigus et a un plus petit diamètre pour compenser le phénomène dissipatif d'écartement vis-à-vis de la longueur d'onde.
Physique-Chimie
Physique
Terminale

Digue et vagues
Cette vidéo traite de l'impact de la diffraction sur les vagues atteignant une digue de port de plaisance et de l'effet de cette diffraction sur deux bateaux se trouvant à proximité. Des vagues de 1 mètre de hauteur sont espacées de 30 mètres et peuvent traverser une passe de 40 mètres. En utilisant les paramètres clés des ondes, l'amplitude d'une vague est de 0,5 mètre, la longueur d'onde est de 30 mètres et la largeur de la fente est de 40 mètres. En appliquant la relation classique pour le calcul de l'angle d'ouverture de diffraction, on obtient θ égal à 0,75 radian, soit 43 degrés. Le bateau 2 est mieux protégé de la houle par la digue que le bateau 1.
Maths
Analyse
MPSI/PCSI

Changement de variable
Dans cette vidéo, Mathis de Studio résout une équation différentielle non linéaire à coefficient non constant. Pour y arriver, il pose une nouvelle variable z qui est égale à y multiplié par exponentielle de t. Il calcule ensuite z' et z'' pour obtenir une équation différentielle linéaire d'ordre 2 à coefficient constant que l'on peut résoudre en posant une solution homogène z_h. Cette solution générale est composée de lambda t plus mu exponentielle de t, où lambda et mu sont des réels. En réinjectant cette solution dans l'équation différentielle, Mathis de Studio obtient les solutions de l'équation, qui sont toutes de la forme lambda x plus mu x carré avec lambda et mu des réels. Finalement, il explique le raisonnement en analyse synthèse pour déduire que l'ensemble des solutions est celui-ci, et que l'on a atteint les deux degrés de liberté nécessaires pour définir l'ensemble des solutions.
Maths
Analyse
MPSI/PCSI

Interprétation géométrique
Dans cette vidéo, Mathis de Studio calcule l'air d'un triangle à l'aide de nombres complexes. Il montre que les complexes ont la même partie imaginaire et que celle-ci est non nulle en utilisant une formule de produit vectoriel. Il introduit ensuite la notion de triangle direct et montre que la partie imaginaire de conjugué de B moins conjugué de A, facteur de C moins A, permet de déterminer si le triangle est direct ou non. Enfin, il montre que 1 demi de la partie imaginaire de conjugué de B moins conjugué de A, facteur de C moins A, est égal à epsilon fois l'air du triangle ABC, où epsilon est un pseudo-symbole de Kronecker, qui vaut 1 si ABC est direct et moins 1 si non. Ce cours complet sur la représentation des nombres complexes en géométrie donne des outils pour résoudre des exercices complexes.
Maths
Analyse
MPSI/PCSI
Somme sinusoïdale
Aucun résumé n'est disponible pour cette vidéo
Maths
Analyse
MPSI/PCSI

Le tour des sommes
Dans cette vidéo, on aborde plusieurs propriétés des nombres complexes.
D'abord, on montre que si les arguments de deux nombres complexes Z et Z' sont les mêmes, alors le conjugé de Z multiplié par Z' appartient à R+ (les réels positifs).
Ensuite, on démontre l'inégalité triangulaire pour le module de la somme de deux nombres complexes. Cette inégalité devient une égalité si et seulement si le produit du conjugé de Z par Z' appartient à R+.
On utilise ensuite une démonstration par récurrence pour montrer que pour n nombres complexes, le module de la somme de ces n nombres est inférieur ou égal à la somme des modules de ces nombres.
On prouve également qu'il y a égalité dans cette inégalité si et seulement si le produit du conjugé de chaque paire de nombres dans la somme appartient à R+.
Enfin, on examine une somme avec des coefficients complexes et on montre que si la somme des ces coefficients est égale à zéro, alors la somme des modules des nombres complexes correspondants est inférieure ou égale à la somme des modules de la différence entre z et chaque nombre.
Cette inégalité devient une égalité si et seulement si le produit du conjugé de chaque coefficient par la différence entre z et chaque nombre appartient à R+.
Le cours se termine en affirmant que si la somme des modules des nombres complexes est inférieure ou égale à la somme des modules des différences entre z et chaque nombre, alors chaque paire de conjugé de coefficient multiplié par la différence entre z et chaque nombre appartient à R+.
Maths
Analyse
MPSI/PCSI

Somme et inégalité
Dans cette vidéo, on étudie les propriétés des nombres complexes.
Tout d'abord, on montre que deux nombres complexes ont les mêmes arguments si et seulement si leur conjugué multiplié ensemble est un nombre réel positif.
Ensuite, on démontre l'inégalité triangulaire pour le module de la somme de deux nombres complexes : le module de la somme est inférieur ou égal à la somme des modules. De plus, cette inégalité devient une égalité si et seulement si le conjugué du produit des deux nombres complexes appartient à l'ensemble des nombres réels positifs.
On généralise ensuite cette inégalité triangulaire pour la somme de n nombres complexes en utilisant la récurrence.
Ensuite, on montre que si la somme des nombres complexes divisés par leur module est égale à zéro, alors la somme des modules de ces nombres est inférieure ou égale à la somme des modules de z moins chaque nombre complexe.
Enfin, on montre que cette inégalité devient une égalité si et seulement si le conjugué de chaque nombre complexe divisé par z moins ce nombre complexe appartient à l'ensemble des nombres réels positifs.
Cette démonstration nécessite une bonne manipulation et calcul des nombres complexes.
Maths
Analyse
MPSI/PCSI

Equations avec arccos arcsin arctan
Dans cette vidéo, Corentin résout cinq équations de trigonométrie. La première équation est arcsinus de x est égal à arccosinus de 1 tiers moins arccosinus de 1 quart. Pour la résoudre, il utilise l'équivalent suivant: y est égal à arcsinus de x si et seulement si sinus de y est égal à x avec y compris entre moins pi sur 2 et pi sur 2. Il en conclut que x est égal à sinus de arccosinus de 1 tiers moins arccosinus de 1 quart, et utilise des formules trigo pour trouver la solution.Pour la deuxième équation, 2x divisé par 1 plus x carré est égal à racine de 3 sur 2, qu'il résout avec le théorème de Pythagore et la résolution d'un polynome de degré 2.La troisième équation est arc tangente de 2x plus arc tangente de 3x est égal à pi sur 4, qu'il résout en passant à la tangente et en appliquant une formule d'addition.La quatrième équation est arc sinus de x plus arc sinus de racine de 1 moins x carré est égal à pi sur 2. Il pose x est égal à sinus de theta, utilise des formules trigo pour simplifier l'équation, et détermine que theta doit être compris entre 0 et pi sur 2.Enfin, la dernière équation n'a pas de solution car arc tangente de 2 et arc tangente de 3 sont strictement supérieurs à pi sur 2, alors que la fonction arc sinus est à valeur dans moins pi sur 2 pi sur 2.
Maths
Analyse
MPSI/PCSI
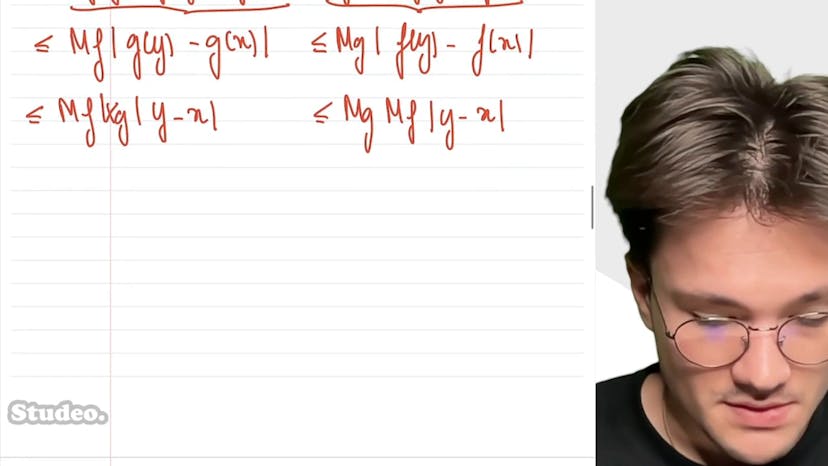
Type Mines : Partie A - 1/4
Dans cette vidéo, Corentin nous présente un exercice sur les fonctions Lipschitzschiene en mathématiques. Il commence par définir les termes et notations importants, puis explore les différentes questions de l'exercice. La première question demande de montrer que l'ensemble des fonctions Lipschitzschiene est non vide et stable par combinaison linéaire. La deuxième question demande de montrer que la composition de deux fonctions Lipschitzschiene est également une fonction Lipschitzschiene. La troisième question explore l'idée que si deux fonctions sont bornées, leur produit est également une fonction Lipschitzschiene. Enfin, Corentin présente un contre-exemple pour prouver que le produit de deux fonctions Lipschitzschiene n'est pas toujours Lipschitzschiene.
Maths
Analyse
MPSI/PCSI

Type Mines : Partie A - 2/4
Ce cours traite de la démonstration de l'existence de deux réels positifs a et b pour toute fonction Lipschitzienne f, telle que pour tout réel x, la valeur absolue de f de x soit inférieure ou égale à a fois la valeur absolue de x plus b. La démonstration repose sur une inégalité triangulaire et sur le caractère Lipschitzien de f. Ensuite, le cours aborde la question de la généralisation de cette propriété pour toutes les fonctions vérifiant que pour tout réel x et y, ayant une distance inférieure ou égale à 1, on a f de y moins f de x inférieur ou égal à m fois y moins x. Pour cela, il est nécessaire de montrer que la fonction en question appartient à l'ensemble des fonctions Lipschitzienne. La démonstration passe par une décomposition et une majoration de la différence de f entre deux réels x et y, d'une distance strictement supérieure à 1, en utilisant une combinaison télescopique et l'inégalité triangulaire. Finalement, la propriété Lipschitzienne est établie, et la fonction est montrée comme étant m-lipschitzienne.


