Cours d'apprentissage en ligne

Existence et Calcul des Primitives

Dans ce cours, nous abordons quelques théorèmes importants sur l'existence des primitives. Tout d'abord, le premier théorème stipule que toute fonction continue sur un intervalle admet des primitives sur cet intervalle. Par exemple, si nous prenons la fonction x², nous pouvons trouver plusieurs types de primitives tels que 3x+2, 3x+5, 3x-pi, etc. Une fois que nous avons trouvé une primitive, nous pouvons en trouver une infinité. Cependant, il est important de noter que l'ensemble de toutes les primitives peut contenir d'autres fonctions que nous n'avons peut-être pas envisagées, mais dans cet exemple, nous avons montré qu'il y en a plus d'une. Le deuxième théorème affirme que pour toute valeur y0 donnée, il existe une unique primitive qui passe exactement par ce point. Par conséquent, si nous fixons un point sur l'axe des ordonnées, il n'y a qu'une seule primitive qui passe par ce point. Par exemple, si nous fixons le point (0,5), il n'y a qu'une seule primitive qui vaudra F(0)=5. Il en va de même pour d'autres points donnés. Il est important de démontrer ces théorèmes, car ils établissent une équivalence entre être une primitive et être de la forme F(x)+k. La démonstration consiste à utiliser une preuve par double implication, où l'on montre que les ensembles des primitives et des fonctions de la forme F(x)+k sont équivalents. En outre, il existe un autre théorème important qui donne les règles de primitives pour des fonctions du type U'+V'. Par exemple, la primitive de U'+V' est U+V, et la primitive de λU' est λU, où λ est une constante. Il est important de mémoriser ces règles, tout comme on mémorise les règles de dérivation. En conclusion, ces théorèmes sont essentiels pour comprendre l'existence des primitives et leurs propriétés. Il est important de les connaître et de comprendre comment les démontrer.

Primitives : condition initiale

Cet exercice porte sur la vérification des primitives d'une fonction présentée, ainsi que la détermination de l'ensemble des primitives et d'une condition initiale. La fonction f est donnée par f(x) = 3x² + 1/x. La première question consiste à vérifier si la fonction F, proposée comme x³ + ln(x), est une primitive de f. Pour cela, il suffit de dériver F et de voir si on obtient f. En dérivant, on obtient bien f(x). Donc F est une primitive de f. Cependant, il faut noter qu'il existe une infinité de primitives, définies à une constante additive près. Dans la deuxième question, on cherche à déterminer l'ensemble des primitives de F et à trouver celle qui prend la valeur 0 en E. Les primitives de F sont de la forme F(x) = x³ + ln(x) + K, où K est une constante réelle. Pour trouver la primitive qui s'annule en E, on utilise la condition initiale F(E) = 0. En substituant E dans F, on obtient l'équation K = -1 - E³. Ainsi, la primitive de F qui s'annule en E est F(x) = x³ + ln(x) - 1 - E³. Cet exercice introduit les méthodes sur les primitives, qui sont utiles pour la résolution des équations différentielles. Si vous avez des questions, n'hésitez pas à consulter la FAQ.

Transformer puis primitiver

Dans ce cours, nous allons voir comment trouver une primitive à partir d'une fonction pour laquelle il n'est pas évident de la trouver. La méthode consiste à identifier la fonction sous la forme d'un produit et à utiliser la décomposition en éléments simples pour les fonctions rationnelles. Dans le premier exemple, la fonction étudiée est f(x) = 3x² + 2x³ + 2x. Nous cherchons à l'exprimer sous la forme "u' fois u". En observant la fonction, nous remarquons que nous pouvons prendre u(x) = x³ + 2x. En dérivant u(x), nous obtenons u'(x) = 3x² + 2, ce qui correspond exactement à la partie "u'" que nous cherchions. Ainsi, la fonction peut s'écrire comme u'(x) * u(x), où u(x) au carré serait une primitive de f(x). En poursuivant, nous cherchons une primitive de f(x) qui prend la valeur 5 pour x = 1. Nous savons que les primitives sont de la forme f(x) + k, où k est une constante réelle. Nous imposons la condition que la primitive prenne la valeur 5 pour x = 1. Après calculs, nous trouvons que k = 1/2. Donc la fonction recherchée est 1/2 * x³ + 2x² + 1/2. Dans le deuxième exemple, nous étudions une nouvelle fonction g(x) qui est également un produit, mais cette fois au dénominateur. Nous utilisons la méthode de décomposition en éléments simples pour transformer la fonction en une somme. Après calculs, nous trouvons que g(x) peut s'écrire comme -1/x + 1/(x-1). Ensuite, nous cherchons la primitive de g(x). Nous calculons la primitive de chaque terme de la somme, ce qui nous donne -ln|x| + ln|x-1|. Cependant, il est important de noter que la primitive de 1/x est ln|x| pour x>0, et ln|x-1| pour x>1. Donc, pour éviter les valeurs absolues, nous pouvons écrire la primitive de g(x) comme ln(x) - ln(x-1) pour x>1. En conclusion, ces deux méthodes nous permettent de trouver des primitives en identifiant des produits et en utilisant la décomposition en éléments simples pour les fonctions rationnelles.

Composition et Primitives

Dans cette vidéo, nous apprenons à repérer des primitifs de fonctions composées. Il est important de reconnaître certaines formes qui reviennent souvent. Par exemple, lorsque nous avons U' sur racine de U, nous savons que la primitive sera deux racines de U. De même, lorsque nous avons cos U fois quelque chose, si c'est U', alors la primitive est sin U. Si nous avons U' fois sin U, la primitive sera moins cos U. Lorsqu'une exponentielle est présente, telle que U' fois E2U, la primitive est E2U. Si nous avons un coefficient du type U' sur U, alors la primitive est ln de U. Lorsque nous avons U' fois U puissance n, la primitive est U puissance n plus 1 sur n plus 1. Pour être sûr de ne pas se tromper, nous pouvons proposer une primitive, la dériver et vérifier si nous obtenons la bonne fonction en retour. Si nous constatons un problème de facteur, nous pouvons ajuster notre proposition. Pour U' sur U puissance n, la primitive est -1 sur n-1 fois 1 sur U puissance n-1. En résumé, nous diminuons le degré au dénominateur de la dérivation pour trouver la primitive. Ensuite, nous examinons les opérations inverses, telles que la racine de U dont la dérivée est U' de racine de U. Comprendre ces opérations inverses nous permet de trouver plus facilement les primitives des fonctions composées. La constante multiplicative n'est pas un problème. Si nous avons une constante incorrecte, nous pouvons simplement la décomposer et ajuster notre valeur. Finalement, nous mettons en pratique ces méthodes pour déterminer les primitives d'une fonction donnée. Dans l'exemple donné, nous devons trouver toutes les primitives sur R de la fonction exponentielle de U. Nous remarquons que la dérivée de notre fonction est 6x, donc nous devons ajouter le facteur 6 pour obtenir la bonne forme. Ainsi, les primitives de la fonction sont de la forme E de 3x² plus 5, multipliée par 1/6 et ajoutée à une constante. En résumé, nous pouvons trouver les primitives d'une fonction composée en reconnaissant les formes courantes et en ajustant si nécessaire.

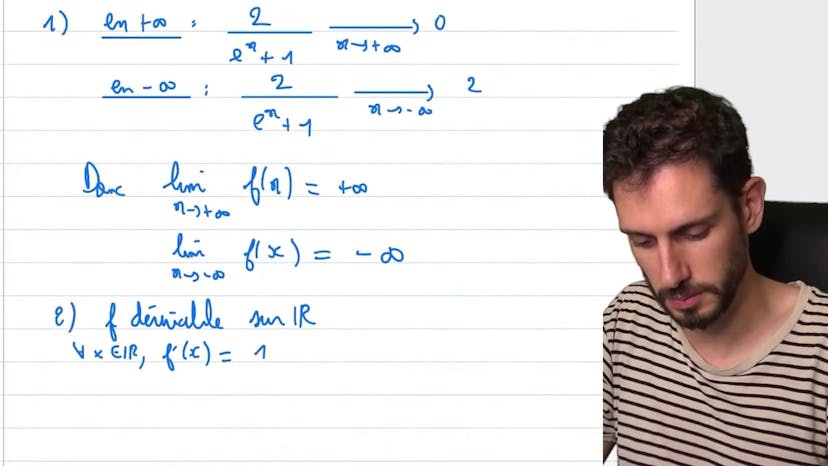
Primitive et réécriture

Dans ce cours, nous étudions une fonction définie par f2x = x + log(4) + 2/(e^(2x) + 1). Nous commençons par analyser cette fonction pour essayer de trouver une expression de primitive facile à détecter. Nous calculons la limite de la fonction lorsque x tend vers l'infini et nous obtenons 0. Pour x tendant vers moins l'infini, la limite est de 2. Ensuite, nous étudions le sens de variation de la fonction et dressons le tableau de variation. Nous montrons que la fonction est dérivable sur R et nous calculons sa dérivée f'2x. En analysant le signe de cette dérivée, nous concluons que f'2x est toujours positif. Par conséquent, la fonction f2x est croissante sur l'ensemble des réels. Pour déterminer les primitives de la fonction, nous remarquons que x et log(4) sont communs dans les différentes expressions de la fonction. Nous obtenons donc une primitive sous la forme x²/2 + (2 + log(4))x. De plus, nous reconnaissons une expression de la forme -2(e^(2x)/(e^(2x) + 1)), que nous pouvons intégrer en utilisant le logarithme. Nous obtenons ainsi une expression de primitive de la forme logarithme de (e^(2x) + 1) + K, avec K appartenant à R.

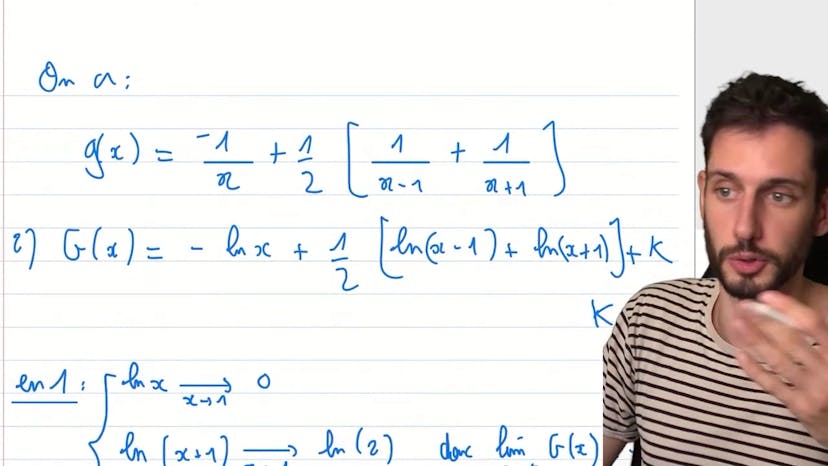
Décomposition en éléments simples

"En MathSup, on apprend à simplifier les fractions rationnelles. On peut le faire de deux façons : en mettant tout au même dénominateur ou en utilisant une méthode plus efficace. Cette méthode consiste à prendre les valeurs de x qui annulent certains termes pour isoler les constantes. En appliquant cette technique, on peut trouver rapidement les constantes a, b et c. Ensuite, on peut déterminer l'ensemble des primitifs de la fonction et ajouter une constante k. Enfin, on peut trouver la limite de la primitive en plus infini et en 1. En utilisant les propriétés du logarithme, on peut réécrire la fonction de manière plus simple. La limite de la fonction tend vers 0, peu importe la constante k."

Polynôme × exponentielle

Ce cours explique comment trouver la primitive d'une fonction contenant une exponentielle. En général, si la fonction est un polynôme multiplié par une exponentielle, sa primitive sera probablement un polynôme du même degré multiplié par l'exponentielle. On apprend également les règles générales de relations entre les primitives et les fonctions. La question 1 demande de trouver la dérivée de la primitive de moins 1, qui est simplement la fonction elle-même. La question 2 demande d'exprimer la dérivée de la fonction en fonction de x, en utilisant les paramètres a et b trouvés dans la question 1. La question 3 demande d'identifier les paramètres a et b en égalant les deux polynômes de la question 2. On trouve que a est égal à moins 1 et b est égal à 3. En utilisant ces valeurs, on trouve que la dérivée de la fonction est moins x plus 3, moins x2 plus 3x, et moins 2x.

Introduction ED

Une équation différentielle est une équation dont l'inconnue est une fonction. Les équations différentielles sont utilisées en physique pour modéliser des phénomènes tels que le mouvement d'un objet ou la variation de température. Par exemple, lorsque l'on tire un boulet de canon, sa vitesse dépend de sa position. La vitesse étant une dérivée de la position, cela donne une équation différentielle. De même, la loi de refroidissement de Newton stipule que la vitesse de refroidissement d'un objet dépend de l'écart entre sa température et la température ambiante, ce qui peut également être modélisé par une équation différentielle. Il existe différents types d'équations différentielles, tels que les équations homogènes et les équations linéaires. Les méthodes de résolution incluent la recherche de solutions particulières ainsi que l'ajout d'une fonction arbitraire dans la solution générale. En conclusion, les équations différentielles sont largement utilisées en physique pour modéliser des phénomènes variables dans le temps.

ED : définitions de base

Le cours traite des équations différentielles homogènes. Ces équations sont de la forme y' = ay, avec a étant un réel non nul. Les solutions de ces équations peuvent toujours s'écrire sous la forme k fois exponentielle à x, avec k étant une constante. Il y a donc une infinité de solutions pour ces équations. Cependant, lorsqu'on fixe une condition initiale, c'est-à-dire une valeur de y à un certain point x0, il n'y a qu'une seule fonction solution qui correspond à cette condition initiale. Il est intéressant de noter que cette fonction solution ressemble à l'exponentielle, ce qui était attendu car l'équation ressemble à la définition de l'exponentielle. Le cours explique ensuite une démonstration de cette propriété des équations homogènes. On commence par faire une démonstration formelle, mais le professeur souhaite montrer l'intuition derrière cette démonstration. Il utilise une approche "physicienne" qui consiste à ignorer certains détails techniques pour trouver une piste de résolution. Il parvient ainsi à montrer que les fonctions solutions sont de la forme exponentielle à x. Cette approche peut sembler choquante en mathématiques, mais elle peut être utilisée pour trouver des pistes de résolution avant de revenir à une démonstration rigoureuse. En utilisant cette intuition, le professeur parvient à poser une nouvelle fonction g(x) qui permet de simplifier la démonstration. Il montre ensuite que la dérivée de g(x) est nulle, ce qui prouve que g(x) est constante. En utilisant cette constante, on peut démontrer que les solutions de l'équation homogène sont bien de la forme exponentielle à x. En conclusion, le cours explique comment les équations différentielles homogènes sont intrinsèquement liées aux fonctions exponentielles, et donne une démonstration de cette propriété en utilisant une approche intuitive.

Solutions Particulières

Les équations différentielles non homogènes sont de la forme Y' = AY + F, où A et F sont des constantes quelconques. La solution de cette équation consiste en la somme d'une solution homogène (Y' = AY) et d'une solution particulière (U' = AU + F). L'ensemble des solutions est donc donné par U + V, avec U solution particulière et V solution homogène. Dans la plupart des cas, on cherche U en s'inspirant de la fonction F. Par exemple, si F est linéaire (3X + 2), on cherche une solution affine (AX + B), et si F est quadratique, on cherche une solution quadratique (AX² + BX + C). On peut appliquer cette méthode de manière systématique, en posant U de la même famille que F. Pour les équations non homogènes avec une fonction constante, la solution particulière est simplement U = -B/1. Cette solution constante est ensuite added to the general solution. Il est important de bien comprendre cette méthode pour résoudre les exercices.

Équation y'=ay

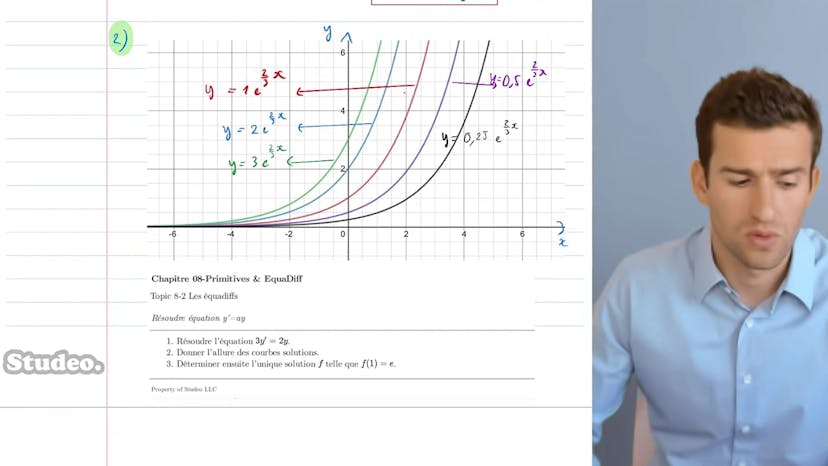
Dans cette méthode, on apprend à résoudre une équation différentielle de premier ordre à coefficient constant, c'est-à-dire une équation du type y' = y. On commence par étudier l'équation différentielle 3y' = 2y en la divisant par 3 pour obtenir y' = (2/3)y. On reconnaît alors la forme y' = y, avec a = 2/3. D'après le cours, on sait que les solutions de cette équation sont de la forme k * e^(ax), soit k * e^(2/3*x) où k est une constante réelle. Ensuite, on nous demande de tracer les courbes solutions de cette équation, en variant la constante k. Plus k augmente, plus la courbe se décolle de l'axe des x, car il s'agit d'une exponentielle avec une constante multiplicative. Toutes les courbes ont donc la même allure. Enfin, on nous demande de trouver la courbe parmi celles-ci qui vérifie f(1) = e. On sait que, pour une équation différentielle avec une condition particulière, il existe une unique solution qui satisfait à la fois l'équation différentielle et la condition particulière. Ici, on veut que f(1) = e, ce qui nous permet de trouver la valeur de k. On suppose que f(x) est de la forme k * e^(2/3*x), on évalue cette expression en x = 1 et on obtient k * e^(2/3) = e. Après résolution, on trouve k = e^(1/3). Donc, la solution recherchée est f(x) = e^(1/3) * e^(2/3*x). C'est une méthode classique pour résoudre une équation différentielle du type y' = y avec une condition initiale. Si vous avez d'autres questions, vous pouvez consulter la FAQ.