 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Analyse
2BAC SM Maroc
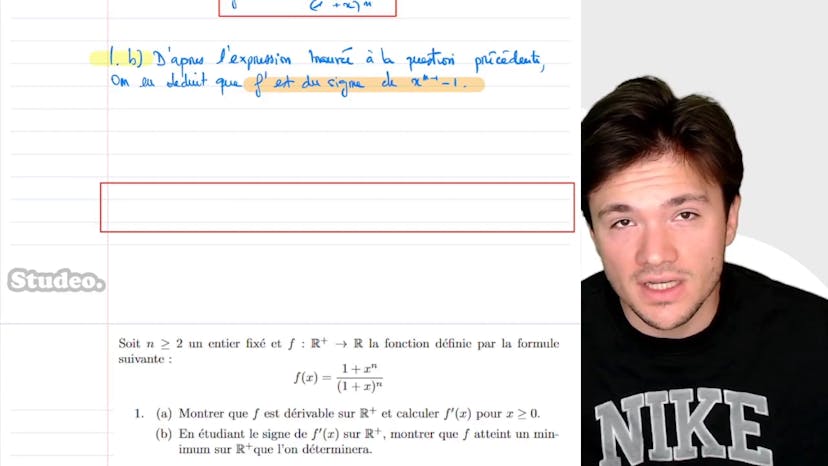
Inégalités par étude de fonction
Dans cette vidéo, Corentin commence par présenter un exercice qui consiste en une étude de fonction. Il demande aux spectateurs de montrer que la fonction f est dérivable sur R+ et de calculer sa dérivée. En étudiant le signe de cette dérivée, il montre que f atteint un minimum en 1.
Ensuite, il aborde une série d'inégalités à démontrer. En utilisant les résultats des questions précédentes, il montre que pour tout x dans R+ , f(2x) est supérieur ou égal à f(2). Il utilise cette inégalité pour établir une deuxième inégalité impliquant des puissances.
Enfin, Corentin démontre une dernière inégalité en se référant aux questions précédentes et en utilisant une équivalence. Il divise l'expression x + y^n par y^n (sous l'hypothèse que y^n est différent de zéro) pour se ramener à une inégalité déjà démontrée. Il conclut que pour tout couple (x,y) dans R+², x + y^n est inférieur ou égal à 2^n - 1 fois x^n + y^n.
En résumé, cet exercice consiste en une étude de fonction suivie par la démonstration de plusieurs inégalités, en utilisant des résultats précédents et en faisant appel à la concentration et aux astuces des spectateurs.
Maths SM&SP
Analyse
2BAC SM Maroc

Racine d’une somme de puissances
Dans cette vidéo, Corentin aborde un exercice mathématique concernant une équation fonctionnelle. L'exercice consiste à démontrer qu'une équation donnée admet une unique racine, puis d'étudier le sens de variation d'une fonction et de calculer des limites.
Pour simplifier les calculs, Corentin passe à l'exponentiel logarithme et obtient une équation équivalente avec une fonction notée f(x). Il calcule certaines valeurs particulières de f, telles que f(0), et remarque qu'elle est strictement positive. Il cherche alors la limite de f lorsque x tend vers l'infini, mais ne peut pas la trouver car il ne connait pas les valeurs exactes des coefficients a (supérieurs à 0 et classés dans l'ordre croissant). Pour contourner ce problème, Corentin divise l'équation par a, ce qui lui permet d'obtenir une expression plus simple et de calculer la limite de cette nouvelle fonction qu'il appelle ftilde. Il trouve que ftilde tend vers -1 lorsque x tend vers l'infini.
Il continue ensuite en calculant la dérivée de f et remarque qu'elle est strictement négative pour tout x dans R, ce qui signifie que f est strictement décroissante. Avec les résultats précédents (f(0) > 0 et limite en l'infini < 0), on peut conclure que f admet une unique racine xA.
Pour étudier le sens de variation de la fonction qui associe A à xA, Corentin revient à la définition fondamentale de la croissance et de la décroissance d'une fonction. En comparant fA(x) et fB(x) pour A < B, il montre que fB(x) ≤ fA(x), donc xB ≥ xA. Ainsi, la fonction est décroissante.
Enfin, Corentin cherche à calculer la limite de xA lorsque A tend vers l'infini. Comme la fonction est décroissante et minorée par 0, la limite est supérieure ou égale à 0. Par raisonnement par l'absurde, il suppose que la limite est différente de 0 et obtient une contradiction. Donc la limite de xA est bien 0. Il montre également que la limite de xA ln(A) est égale à ln(P), en remplaçant dans l'équation donnée.
En résumé, cet exercice permet de démontrer l'existence et l'unicité d'une racine d'une équation fonctionnelle, d'étudier le sens de variation d'une fonction associant A à cette racine, et de calculer des limites.
Maths SM&SP
Analyse
2BAC SM Maroc

Dérivée n-ième
Bonjour à tous, c'est Corentin. Aujourd'hui, nous avons un exercice complexe qui demande beaucoup de calculs et de concentration. L'énoncé nous demande de dériver n fois la fonction f(x) = x²ln(1+x). Nous utilisons la formule de Leibniz pour cela. On identifie les fonctions g(x) = x² et h(x) = ln(1+x). On commence par dériver h(x) et trouvons que h'(x) = 2x, h''(x) = 2, et h''''(x) = 0 pour tout k ≥ 3. Pour g(x), nous trouvons que g'(x) = 1+x, g''(x) = -(1/(1+x)²), et g''''(x) = -((k-1)!(1+x)^(-k)). En utilisant la formule de Leibniz, nous trouvons que la dérivée n-ième de f(x) est égale à la somme de (kCn)(g^(k))(h^(n-k)) pour k allant de 0 à n. En factorisant et simplifiant, nous trouvons finalement que f^(n)(x) = 2x² + 2nx + n² - n(1/(1+x)^(n)). Cet exercice est complexe dans les calculs, mais la clé est de simplifier les expressions et de découper le travail. Il est important d'identifier la formule de Leibniz comme outil nécessaire pour résoudre cet exercice. La qualité de la paresse peut être utile ici, car elle nous pousse à simplifier les expressions et à rendre le travail plus facile.
Maths SM&SP
Analyse
2BAC SM Maroc
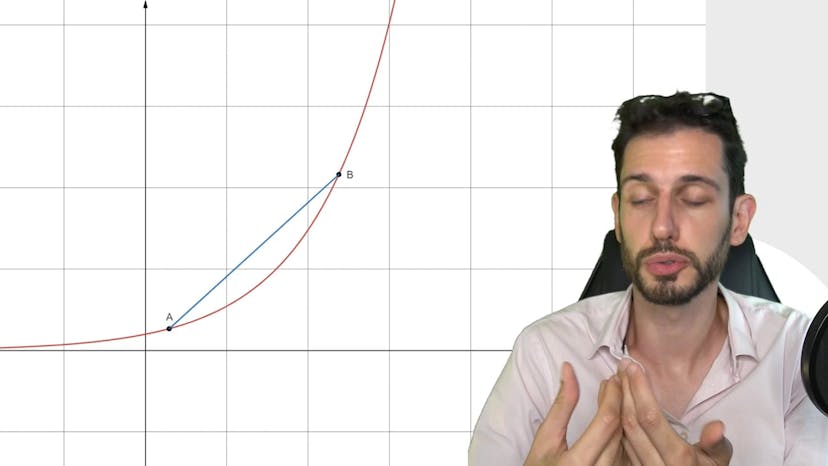
Intuition et déf
Dans cette première vidéo sur la convexité, nous abordons les différentes définitions de la convexité. Nous commençons par une explication simple à l'aide d'un graphique : la convexité fait référence à une courbe qui semble monter de plus en plus, tandis que la concavité fait référence à une courbe qui monte mais pas trop rapidement. Une autre façon de se rappeler des concepts est de penser à la convexité comme un sourire et à la concavité comme une tranche. Ensuite, nous introduisons la définition mathématique officielle, qui est basée sur les séquentes ou les cordes. Une séquente est une droite qui relie deux points d'une courbe. Une fonction est convexe si sa courbe est en dessous de toutes ses séquentes, et elle est concave si elle est au-dessus de toutes ses séquentes. Pour illustrer cela, nous regardons des graphiques de fonctions convexes et concaves et vérifions si leur courbe se trouve au-dessus ou en dessous de leurs séquentes. Il est important de noter que dans cette définition, il n'y a pas de mention de continuité ou de dérivabilité. On peut être convexe ou concave même si la fonction n'est pas dérivable. C'est tout pour cette vidéo de présentation et la définition de base de la convexité. À bientôt dans la prochaine vidéo. Au revoir.
Maths SM&SP
Analyse
2BAC SM Maroc

Fonctions usuelles
Ce cours aborde les fonctions classiques en mathématiques. Il explique que les fonctions racine et logarithme sont concaves, ce qui signifie qu'elles ressemblent à un sourire dans leur représentation graphique. En revanche, la fonction 1/x est convexe sur R+ et concave sur R-. Une petite règle intuitive est également donnée : les fonctions x puissance alpha, avec alpha entre 0 et 1, sont concaves (comme les racines), tandis que les fonctions x puissance alpha avec alpha supérieur à 1 sont convexes. La fonction y=x est à la fois convexe et concave car elle est une droite. Enfin, quelques exemples de tracés de fonctions sont donnés pour illustrer ces propriétés. Cela concerne des fonctions du type x puissance alpha, avec alpha allant de 0 à 2. On peut voir que les fonctions avec alpha entre 0 et 1 sont concaves, tandis que pour alpha supérieur à 1, elles sont convexes.
Maths SM&SP
Analyse
2BAC SM Maroc

Inégalité fondamentale
Dans cette vidéo, nous allons étudier la relation entre une courbe et ses sécantes pour traduire la convexité d'une fonction. Une fonction convexe est située en dessous de ses sécantes. Pour illustrer cela, nous avons un graphique avec une courbe rouge située sous les sécantes bleues. L'objectif est de comparer la différence d'ordonnée entre un point sur la sécante bleue et un point sur la courbe rouge pour une même abscisse entre les points A et B. En prenant une abscisse intermédiaire, représentée par le point T, nous pouvons démontrer que le point sur le segment est plus haut que le point sur la courbe rouge. Ainsi, nous concluons qu'il y a une inégalité entre ces deux points. En utilisant cette notion, nous pouvons considérer un point d'abscisse intermédiaire entre A et B, que nous appelons T, en pondérant les abscisses de A et B. En observant l'image de ce point T par la fonction courbe, notée F, nous constatons qu'elle est inférieure à l'image de cette abscisse par l'équation de la sécante. Il peut être difficile de comprendre cette équation rapidement, mais nous pouvons fournir une démonstration complète pour ceux qui sont intéressés. En résumé, cette vidéo explique comment traduire la relation entre une courbe et ses sécantes dans le contexte de la convexité d'une fonction. De plus, il est important de noter le lien logique entre la convexité et la concavité : si F est convexe, alors moins F est concave, et vice versa. Une démonstration complète est disponible dans une autre vidéo. Si vous avez des questions, n'hésitez pas à les poser sur le forum. Merci de votre attention et rendez-vous dans la prochaine vidéo.
Maths SM&SP
Analyse
2BAC SM Maroc

Lien dérivation
Dans ce cours, nous abordons la convexité d'une fonction dérivable. Nous rappelons que la convexité ne dépend ni de la continuité, ni de la dérivabilité de la fonction, mais seulement de la position entre les séquentes et la courbe de la fonction.
Nous simplifions la définition pour la rendre plus pratique pour une utilisation quotidienne. Nous expliquons que f est convexe sur un intervalle i si, pour tout réel x de cet intervalle, f' est croissante. De même, f est concave sur i si f' est décroissante.
Nous illustrons cela avec l'exemple de la fonction cubique. Nous observons que la fonction est concave au début et convex à la fin. Nous expliquons que cela correspond à la décroissance de la dérivée f', puis à son augmentation.
Nous utilisons également la dérivée seconde pour étudier la convexité. Nous expliquons que si f est deux fois dérivable et que f' est positive, alors f est convexe. Ainsi, plutôt que de comparer les courbes et les droites, il suffit de calculer la dérivée seconde f'' pour déterminer la convexité.
En conclusion, il est plus pratique d'étudier la convexité d'une fonction dérivable en calculant sa dérivée seconde. Cela simplifie l'étude en réduisant l'analyse à un simple calcul de dérivée.
Maths SM&SP
Analyse
2BAC SM Maroc
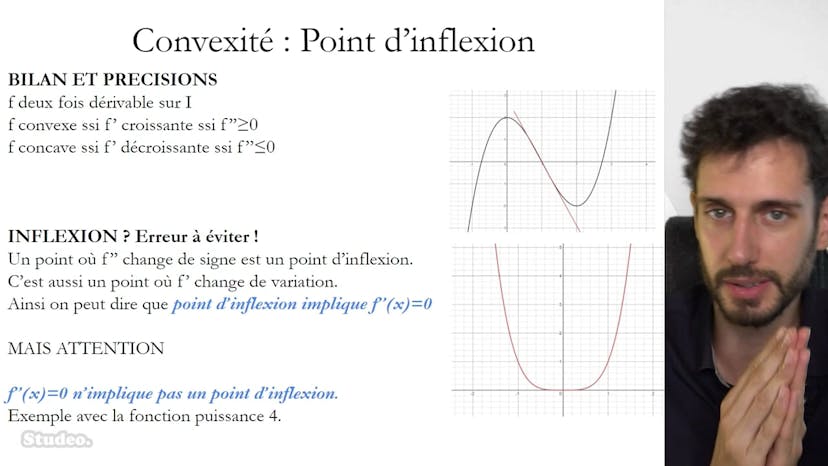
Point d'inflexion
Le cours présente la notion de point d'inflexion dans le contexte des fonctions dérivables. Un point d'inflexion est défini comme un endroit où la courbe d'une fonction traverse sa tangente, correspondant à un changement de comportement entre concavité et convexité. Il est également noté que le point d'inflexion correspond à un point de pente maximale de la tangente, où la pente devient la plus négative en valeur absolue. De plus, le cours rappelle que la convexité d'une fonction est liée à la positivité de sa dérivée première, tandis que la concavité est liée à la négativité de sa dérivée première. Enfin, il est souligné qu'un point d'inflexion implique un changement de signe de la dérivée seconde, mais que l'inverse n'est pas toujours vrai, comme illustré par des exemples.
Maths SM&SP
Analyse
2BAC SM Maroc

Démo inégalité convexité
Dans ce cours, nous prenons les points réels X et Y, ainsi que les points associés A et B. Nous avons une séquence illustrée par un dessin, ainsi qu'un point M défini par les coordonnées Apcis (TX+1-TY) et (TF2X+1-TF2Y). Nous allons démontrer que cette ordonnée est bien sur la séquence.
Pour cela, nous analysons la position de l'apcis entre X et Y, ainsi que l'ordonnée entre TF2X et TF2Y, afin de montrer qu'elle est bien sur la séquence. Nous démontrons aussi que M appartient au segment AB en vérifiant que les Apcis de M et de Y sont comprises entre les Apcis de A et B.
Ensuite, nous vérifions que M est sur la droite AB en utilisant l'équation de la droite, où Y est égal à AlphaX+Beta. Nous calculons Alpha en utilisant les variations des ordonnées et des Apcis entre A et B, et nous trouvons Beta en utilisant le fait que le point A est sur la droite.
Pour vérifier que M est sur la droite, nous remplaçons l'apcis de M à la place de X dans l'équation et espérons obtenir l'ordonnée de M à la fin du calcul. En effectuant les calculs, nous trouvons que l'apcis de Y correspond à l'ordonnée de M, ce qui confirme que M est sur la droite.
En conclusion, en démontrant que M appartient au segment AB qui est sur la séquence CF, nous pouvons affirmer que l'image de l'apcis de M par la séquence est au-dessus de son image par F.
Maths SM&SP
Analyse
2BAC SM Maroc

Démo au programme : convexité et f''
Dans ce cours, on étudie les propriétés graphiques d'une fonction et leur lien avec sa dérivée seconde. Si f'' (la dérivée seconde de f) est positive sur l'intervalle i, alors la courbe représentative de f est au-dessus de ses tangentes. Cela rappelle la définition de la convexité, où la courbe est au-dessus de ses cordes.
La démonstration de ce fait commence par une introduction, qui indique les hypothèses de départ et ce qu'on veut montrer. Ensuite, on met tout du même côté pour simplifier l'expression, puis on pose une fonction qui compare la courbe et la tangente au point a. On étudie cette fonction, en montrant qu'elle est dérivable et en cherchant le signe de sa dérivée. Puis, on utilise le fait que la dérivée seconde est positive pour conclure que la dérivée est croissante. Enfin, on fait un tableau de variation de la fonction pour montrer qu'elle est toujours positive ou nulle. Cela prouve que la courbe est au-dessus de la tangente.
Pour bien comprendre cette démonstration, il est important de reprendre chaque étape et de savoir les réécrire sans aide. Cela permet de maîtriser parfaitement le sujet.
Maths SM&SP
Analyse
2BAC SM Maroc
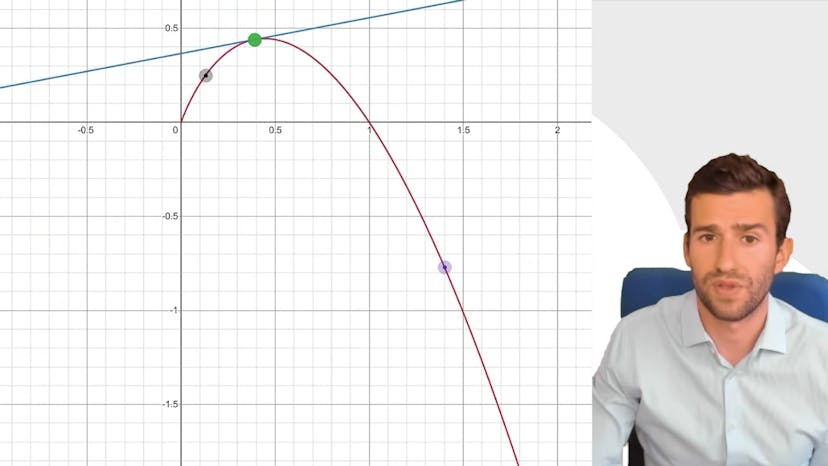
Convexité et f''
La convexité d'une fonction est un chapitre important en mathématiques. En étudiant la convexité d'une fonction, on peut trouver des propriétés intéressantes, comme la position de la tangente par rapport à la courbe. Dans cet exemple, nous étudions la fonction f(x) = (1/3)x^3 - (3/2)x^2 + 2x + 1. Cette fonction est un polynôme, donc dérivable au moins deux fois. Nous regardons le signe de la dérivée seconde pour déterminer si la fonction est concave ou convexe. La dérivée seconde de f(x) est 2x - 3. Cette dérivée seconde est positive pour x > 3/2 et négative pour x < 3/2. Cela signifie que f(x) est concave pour x < 3/2 et convexe pour x > 3/2. Dans le deuxième exemple, nous étudions la fonction f(x) = 3x - 3x^(3/2). Cette fonction n'est pas définie pour x < 0 et n'est pas dérivable en x = 0. Nous calculons la dérivée seconde qui est -9/(4√x). Comme √x est toujours positif, la dérivée seconde est toujours négative. Nous concluons que f(x) est concave sur tout son ensemble de définition. En termes d'interprétation, cela signifie que la courbe est toujours située sous les tangentes. On peut également dire que la courbe est au-dessus des cordes définies par deux points sur la courbe. La concavité et la convexité permettent de déterminer la position relative de la tangente par rapport à la courbe.
Maths SM&SP
Analyse
2BAC SM Maroc
Convexité et Inégalités
Dans cette leçon, nous abordons la méthode de la convexité. Il s'agit d'une approche classique, mais extrêmement utile une fois que l'on maîtrise son étude.
Nous commençons par examiner une fonction f(x) = x³ - 2x². Comme il s'agit d'un polynôme, il est dérivable deux fois sans problème. Nous calculons ensuite ses deux dérivées : f'(x) = 3x² - 4x et f''(x) = 6x - 4.
Notre objectif est d'étudier le signe de f''(x). Nous résolvons l'inéquation 6x - 4 > 0, ce qui nous donne x > 3/2. En revanche, si f''(x) < 0, cela signifie que x < 3/2. Nous en déduisons donc la concavité et la convexité de la fonction f : f est concave sur l'intervalle ]-∞, 3/2[ et convexe sur l'intervalle ]3/2, +∞[.
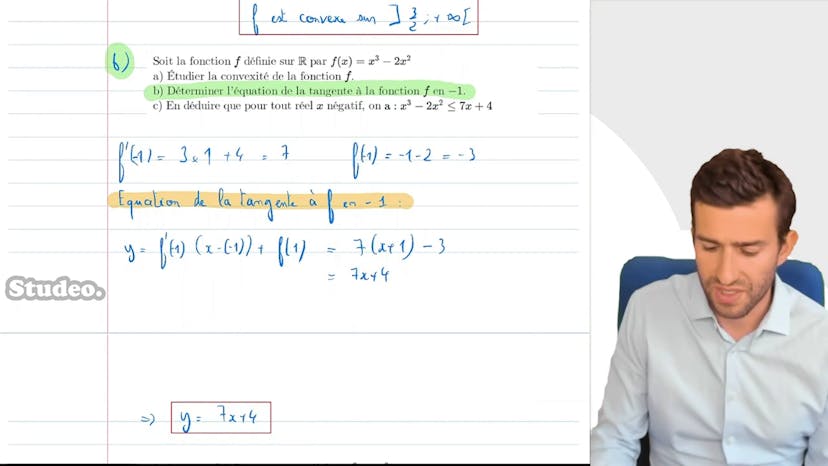
Ensuite, on nous demande de trouver l'équation de la tangente à la courbe de f au point x = -1. Nous appliquons les formules appropriées : l'équation de la tangente au point x = -1 est f'(-1) * x - (-1) + f(-1). Suite à nos calculs précédents, nous trouvons que f'(-1) = 7 et f(-1) = -3. Ainsi, l'équation de la tangente est y = 7x + 4.
Enfin, on nous demande de prouver que pour tout x négatif, x³ - 2x² < 7x + 4. Nous constatons que 7x + 4 est l'équation de la tangente que nous avons précédemment trouvée, et x³ - 2x² est équivalent à f(x). En analysant géométriquement cette inégalité, nous concluons que la courbe de f est située en dessous de sa tangente lorsque f est concave. Comme nous avons prouvé précédemment que f est concave sur l'intervalle ]-∞, 3/2[, nous pouvons affirmer que cette inégalité est vraie pour tout x négatif.
Il est essentiel de comprendre le concept de convexité lors de la résolution de ce problème. Si nous ne l'appliquons pas, nous nous retrouverons avec une équation de degré 3, ce que nous ne savons pas résoudre. La méthode de la convexité est donc indispensable.
N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires.


