 All subjects
All subjects
 All subjects
All subjects
Maths SM&SP
Algèbre
2BAC SM Maroc

Décomposition en facteurs premiers
Dans cet exercice, nous cherchons les couples d'entiers (A, B) qui satisfont l'équation 3 * (21^A) = 14 * (9^B). Pour résoudre ce problème, nous utilisons la décomposition en facteurs premiers. En effet, afin d'identifier les puissances dans le produit, nous devons décomposer l'équation en facteurs premiers. La décomposition en facteurs premiers d'un nombre est unique, donc la décomposition de 3 * (21^A) est identique à celle de 14 * (9^B).
Nous commençons par la partie gauche de l'équation, en décomposant 3 et en nous concentrant sur (21^A). Nous décomposons ainsi (21^A) en 3 * (7^A). Puis, nous utilisons les règles de calcul des puissances pour obtenir (3^A) * (7^A) à partir de (3 * (7^A)). En réorganisant le calcul de base, nous obtenons (3^(A+1)) * (7^A) pour 3 * (21^A). Ainsi, nous avons décomposé 3 * (21^A) de manière unique en (3^(A+1)) * (7^A).
Nous faisons la même décomposition pour la partie droite de l'équation. En décomposant 14, nous obtenons 2 * 7. Et en décomposant 9, nous obtenons 3^2. Utilisant ensuite la règle de calcul des puissances, nous obtenons 2 * (3^(2B)) * 7^B pour 14 * (9^B).
Pour que les deux produits soient identiques, nous devons trouver des valeurs de A et B qui satisfont cette équation. Cependant, le problème est que le facteur 2 apparaît dans la décomposition de 14 * (9^B), mais n'apparaît pas dans la décomposition de 3 * (21^A). Étant donné qu'A et B concernent le 3 (éventuellement le 7 aussi), mais pas le 2, nous ne pouvons pas compenser le facteur 2 avec A ou B. Par conséquent, il n'y a aucune valeur de A et B qui vérifie cette équation. Ainsi, nous concluons que l'équation n'a pas de solution.
Maths SM&SP
Algèbre
2BAC SM Maroc

Critère d'arrêt : n est premier ?
Dans cet exercice, nous utilisons le critère d'arrêt pour déterminer si un nombre est premier ou non. Le critère d'arrêt stipule que si un nombre n'est pas premier, il a un diviseur premier P compris entre 2 et la racine carrée de ce nombre. Nous n'avons pas besoin de tester tous les nombres premiers jusqu'au nombre que nous voulons tester pour savoir s'ils le divisent ou non. Nous devons simplement les tester jusqu'à la racine carrée de n.
Dans cet exercice, nous calculons la racine carrée de 349, ce qui donne environ 18,7. Par conséquent, nous devons tester tous les nombres premiers inférieurs ou égaux à 18,7. Nous nous arrêtons à 17, ce qui signifie que nous devons tester si 2, 3, 5, 7, 11, 13 et 17 divisent 349. Ces nombres premiers doivent être connus, puisqu'ils sont utilisés régulièrement dans les exercices.
En testant ces nombres, nous constatons rapidement qu'aucun d'entre eux ne divise 349. Par conséquent, nous concluons que 349 est un nombre premier. Cela conclut l'exercice sur l'utilisation du critère d'arrêt.
Maths SM&SP
Algèbre
2BAC SM Maroc

Démo infinité des premiers
Dans cet exercice, nous allons montrer qu'il existe une infinité de nombres premiers. Pour cela, nous supposons que l'ensemble des nombres premiers est fini, et nous allons parvenir à une contradiction.
Nous commençons par noter P comme étant l'ensemble des nombres premiers, et nous supposons qu'il contient N nombres, notés P1, P2, P3... jusqu'à PN.
Nous construisons ensuite un nouveau nombre appelé P étoile, qui est le produit de tous les nombres premiers de l'ensemble P, auquel nous ajoutons 1.
La première étape consiste à montrer que pour chaque indice i appartenant à N, le nombre Pi ne divise pas P étoile. Nous utilisons une démonstration par l'absurde et supposons qu'il existe un indice i pour lequel Pi divise P étoile. Cependant, P étoile est congru à 1 modulo Pi, ce qui contredit le fait que Pi divise P étoile. Ainsi, aucun nombre premier de l'ensemble P ne divise P étoile.
Ensuite, nous montrons que P étoile est strictement plus grand que le plus grand des nombres premiers de l'ensemble P. Par conséquent, P étoile ne peut pas être un nombre premier.
Cependant, selon le critère d'arrêt, il existe un nombre premier Pi dans l'ensemble P qui divise P étoile. Cela contredit ce que nous avons prouvé dans la première étape, où nous avons montré qu'aucun nombre premier de l'ensemble P ne divise P étoile.
Cette contradiction prouve que notre supposition selon laquelle l'ensemble des nombres premiers est fini est fausse. Par conséquent, il existe une infinité de nombres premiers.
Cela conclut l'exercice.
Maths SM&SP
Algèbre
2BAC SM Maroc

Décomposition et équation
Dans cet exercice, nous devons résoudre l'équation x(x+1)(2x+1) = 84 pour trouver les solutions entières. Pour cela, nous commençons par décomposer 84 en facteurs premiers, ce qui nous donne 2^2 * 3 * 7. Ensuite, nous examinons toutes les possibilités d'écrire 84 comme un produit de 3 facteurs distincts, en tenant compte du fait que x, x+1 et 2x+1 doivent tous être différents. Nous constatons que 2*6*7 n'est pas une option car 2x+1 serait plus petit que x+1. En revanche, 2*3*14 et 3*4*7 sont des options valides. En analysant chaque possibilité, nous trouvons que seule la deuxième option fonctionne, avec x=3. Ainsi, la solution de l'équation dans ce cas est x=3.
Maths SM&SP
Algèbre
2BAC SM Maroc

Nombre de diviseurs
Dans cet exercice, nous devons compter le nombre de diviseurs du nombre 300 puissance 300. Pour cela, nous devons décomposer 300 puissance 300 en facteurs premiers, puis conclure avec le nombre de diviseurs de ce nombre.
Nous commençons par remarquer que 300 est égal à 3 fois 10, ce qui est équivalent à 3 fois 2 au carré fois 5 au carré. En élevant cela à la puissance 300, nous obtenons 3 puissance 300 fois 2 au carré fois 5 au carré puissance 300.
En distribuant la puissance dans le produit, nous obtenons 3 puissance 300, 2 au carré fois 300 et 5 au carré fois 300. Il s'agit de puissances de puissance, donc nous multiplions les exposants, ce qui donne 2 puissance 600 et 5 puissance 600.
Maintenant, pour déterminer le nombre de diviseurs, nous utilisons une formule : si nous avons la décomposition en facteurs premiers d'un nombre n égale à p1 puissance alpha 1 fois p2 puissance alpha 2, etc., alors le nombre de diviseurs est égal à (alpha 1 + 1) fois (alpha 2 + 1), etc.
En utilisant cette formule, nous prenons toutes les puissances et nous leur ajoutons 1, puis nous multiplions tout cela. Dans le cas de 300 puissance 300, nous avons 301 fois 601 fois 601 diviseurs, ce qui donne un total de 108 721 501 diviseurs.
Maintenant, pour la deuxième question qui demande de trouver un nombre ayant plus d'un milliard de diviseurs, nous remarquons que nous sommes déjà très proches avec 108 721 501 diviseurs. Nous devons juste trouver un moyen de multiplier ce nombre par 10 pour atteindre le milliard.
En prenant par exemple la puissance 9, cela ajoute 10 diviseurs (puisque 9 + 1 = 10). En multipliant tous les diviseurs par 10 dans la formule, nous atteignons le milliard de diviseurs pour 300 puissance 300 fois 7 puissance 9.
Maths SM&SP
Algèbre
2BAC SM Maroc

Utiliser Fermat 1/2
Dans cet exercice, nous devons démontrer que, pour tout nombre premier P différent de 3 et tout nombre naturel n, l'expression 3^n + P - 3^(n+1) est divisible par P.
Nous allons utiliser le théorème de Fermat pour résoudre cet exercice. Le théorème de Fermat stipule que, si A est un nombre entier et P est un nombre premier qui ne divise pas A, alors A^P - 1 est congru à 1 modulo P.
Nous voulons montrer que 3^n + P - 3^(n+1) est congru à 0 modulo P. Pour cela, nous allons voir si nous pouvons utiliser le théorème de Fermat.
Dans l'énoncé, il est précisé que nous avons un nombre premier différent de 3. Étant donné que P est premier et différent de 3, cela signifie simplement que P ne divise pas 3. Par conséquent, nous pouvons appliquer le théorème de Fermat avec 3 et P.
D'après le petit théorème de Fermat, nous avons 3^P - 1 est congru à 1 modulo P.
Maintenant, nous allons utiliser ce résultat. Nous voulons faire apparaître les puissances 3^(n+P) et 3^(n+1). Nous allons donc multiplier cette congruence par 3^(n+1). Avant cela, nous allons tout passer d'un côté pour obtenir 0.
Donc, en multipliant par 3^(n+1), nous obtenons 3^(n+1) * (3^P - 1) - 3^(n+1).
Maintenant, nous avons obtenu la puissance que nous recherchions, à savoir 3^(n+1). Et comme nous avons deux puissances de 3 différentes en produit, nous additionnons les exposants. Donc, cela devient (n+1) + (P-1) = n + P.
Finalement, nous avons démontré que 3^n + P - 3^(n+1) est congru à 0 modulo P.
Maths SM&SP
Algèbre
2BAC SM Maroc

Utiliser Fermat 2/2
Le petit théorème de Fermat est utilisé pour montrer que pour tout nombre premier P et nombre entier A qui n'est pas divisé par P, A puissance P moins 1 est divisible par P. Dans le premier exercice, on montre que 4 puissance 28 moins 1 est divisible par 29 en appliquant le petit théorème de Fermat.
Dans le deuxième exercice, on montre que pour tout n, 4 puissance n moins 1 est divisible par 3 en utilisant les congruences et en remarquant que 4 est congru à 1 modulo 3.
Dans le troisième exercice, on montre que pour tout k, 4 puissance 4k moins 1 est divisible par 5 et par 17, en utilisant les congruences et en remarquant que 4 puissance 4 est congru à 1 modulo 5 et modulo 17.
Enfin, dans la dernière question, on déduit que 4 puissance 28 moins 1 a quatre diviseurs premiers, à savoir 3, 5, 17 et 29, en utilisant les résultats précédents.
Maths SM&SP
Algèbre
2BAC SM Maroc

Vers la sup : racine puissance n
Dans cet exercice, nous utilisons le théorème de Bézout pour calculer différentes expressions. Nous commençons par calculer 1 plus la racine carrée de 6 au carré, 1 plus la racine carrée de 6 puissance 4 et puissance 6, en utilisant les identités remarquables et les calculs simples. Ensuite, nous décomposons en facteurs premiers les nombres obtenus et observons qu'ils sont premiers entre eux, car ils n'ont aucun diviseur commun.
Ensuite, nous généralisons ces calculs en utilisant n au lieu de carré, 4 ou 6, et nous trouvons les valeurs de an et bn correspondantes.
Nous calculons également an plus 1 et bn plus 1 en fonction de an et bn, en appliquant les règles de calcul des puissances.
Enfin, nous démontrons que si 5 ne divise pas an plus bn, alors 5 ne divise pas non plus an plus 1 et bn plus 1, en utilisant la contraposée. Nous utilisons les propriétés de la somme de deux nombres divisibles par 5 pour montrer que si 5 divise an plus 1 et bn plus 1, alors il divise également an plus bn.
En conclusion, nous démontrons que si an et bn sont premiers entre eux, alors an plus 1 et bn plus 1 sont également premiers entre eux. Nous concluons également que les valeurs de an et bn trouvées précédemment sont toujours premières entre elles. L'exercice se termine en expliquant que ces résultats sont généralisables et en prouvant qu'ils sont vrais pour tous les n.
Maths SM&SP
Algèbre
2BAC SM Maroc

Congruence : équation degré 2
Dans cet exercice, nous devons résoudre l'équation x²-2x+2≡0 (mod 17) en utilisant l'équation du second degré en congruence. Tout d'abord, nous devons montrer que α=5 est une solution de l'équation E. En remplaçant x par 5, nous obtenons 25-10+2=17, qui est congruent à 0 modulo 17. Donc, α est bien une solution de E.
Ensuite, nous posons x̄=x-α pour trouver toutes les solutions de E. En remplaçant x par x̄+α dans l'équation E, nous obtenons (x̄+α)²-2(x̄+α)+2≡0 (mod 17). En développant l'équation, nous obtenons x̄²+8x̄≡0 (mod 17).
Nous factorisons l'équation en utilisant la congruence à 0 modulo 17, ce qui nous donne x̄(x̄+8)≡0 (mod 17). Selon le lemme de Gauss, puisque 17 est premier et qu'il divise le produit, il divise soit x̄ soit (x̄+8). Nous avons donc deux possibilités à étudier :
1) Si 17 divise x̄, cela signifie que x≡5 (mod 17).
2) Si 17 divise (x̄+8), cela signifie que x≡14 (mod 17).
Ainsi, toutes les solutions de E sont x≡5 (mod 17) ou x≡14 (mod 17).
Maths
Algèbre
MPSI/PCSI

Nombres de Fermat
Dans cet exercice, le but est de montrer que si M est un nombre entier positif tel que 2 puissance M plus 1 soit un nombre premier, alors M est une puissance de 2.
Pour cela, on développe une égalité : X puissance Q plus 1 est égal à X plus 1 fois X puissance Q moins 1, moins X puissance Q moins 2, plus X puissance Q moins 3, etc., jusqu'à plus 1.
Ensuite, en simplifiant cette équation, on remarque que si Q est impair, toutes les puissances paires de X ont un signe plus, ce qui fait apparaître le plus 1 nécessaire pour que 2 puissance M plus 1 soit premier.
Donc on peut conclure que M est une puissance de 2.
En utilisant cette propriété, on montre par l'absurde que si 2 puissance M plus 1 est premier et M n'est pas une puissance de 2, cela conduit à une contradiction.
Donc on en déduit que M est nécessairement une puissance de 2.
Maths
Algèbre
MPSI/PCSI

Nombres de Mersenne
Dans cette vidéo, on aborde le sujet des nombres de Mersenne.
Le premier objectif est de démontrer que si a^(n-1) est premier, alors a est égal à 2 et n est premier.
Pour cela, on factorise a^(n-1) avec a-1, a^(n-2), ..., jusqu'à 1. On remarque que 1-1 divise a^(n-1), tandis que a-1 est différent de a^(n-1) car n est supérieur ou égal à 2. Donc a-1 est égal à 1, ce qui implique que a est égal à 2.
Ensuite, il faut prouver que n est premier. On note n comme p*q, et on réécrit une égalité factorisée avec 2^(n-1). On observe que 2^(p-1) divise 2^(pq-1), qui est égal à 2^(n-1). Donc, si 2^(p-1) est égal à lui-même, cela signifie que p est égal à n. Ainsi, q est égal à 1 dans cette factorisation. De plus, si 2^(p-1) est égal à 1, cela entraîne que p est égal à 1. Donc, q est égal à n. Ainsi, dans tous les cas, n est un nombre premier.
Ensuite, on doit vérifier que M11 n'est pas premier. On calcule M11, qui est égal à 2^11 - 1, soit 2047. On peut le décomposer en 23 fois 89, ce qui prouve que ce n'est pas un nombre premier.
Le but de cette question est de comprendre pourquoi on nous l'a posée. On a vu précédemment que si un nombre de Mersenne est premier, alors la puissance n est aussi premier. Cependant, on vient de prouver le contre-exemple que si n est premier, alors 2^11 - 1 n'est pas premier. Donc, on a démontré que la réciproque ne marche pas.
Maths
Algèbre
MPSI/PCSI
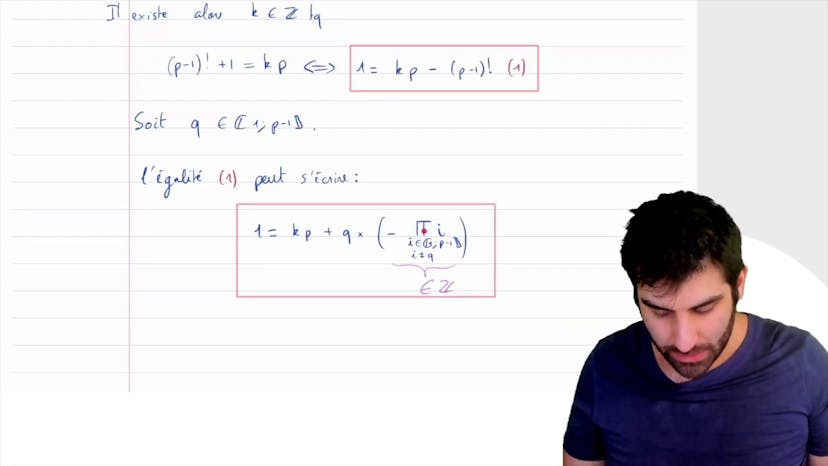
Théorème de Wilson
Dans cet exercice, nous allons démontrer que si P est un entier supérieur ou égal à 2 et que P-1! est congruent à -1 modulo P, alors P est premier. Nous allons démontrer cette implication dans un sens pour l'instant.
Nous partons donc du constat que P-1! est congruent à -1 modulo P, ce qui signifie qu'il existe un entier k tel que P-1! + 1 = k * P. En réarrangeant cette équation, nous obtenons 1 = k * P - (P-1!), que nous nommons équation 1 pour référence ultérieure.
Notre méthode pour prouver que P est premier consiste à montrer que P est premier avec tous les nombres plus petits que lui. Si tel est le cas, alors P est effectivement un nombre premier.
Nous prenons donc un nombre Q plus petit que P et dans l'intervalle [1, P-1!]. En réécrivant l'équation 1 comme 1 = k * P + Q * (P-1!), nous remarquons que le produit des entiers i dans l'intervalle [1, P-1!] (à l'exception de Q) est égal à P-1!. Nous avons également le terme -1.
Ce produit est un entier relatif, plus précisément un entier négatif, ce qui n'est pas important pour notre démonstration. Ce qui est important, c'est qu'il s'agit d'un entier. Nous pouvons donc considérer cette équation comme une équation de Bézout, où k * P et Q * (P-1!) sont premiers entre eux, selon le théorème de Bézout.
Ainsi, en prenant Q de manière arbitraire, nous avons démontré que P est premier avec tous les entiers plus petits que lui. Par conséquent, P est nécessairement un nombre premier.
Ceci conclut notre exercice.
Maths
Algèbre
MPSI/PCSI

Petit théorème de Fermat
Dans cet exercice, on étudie le petit théorème de Fermat en utilisant la méthode de récurrence sur A. On veut montrer que pour tout entier k compris entre 1 et p-1, le coefficient binomial p divise k parmi p. Pour cela, on utilise la définition du coefficient binomial k parmi p, qui est p factoriel divisé par p-k factoriel fois k factoriel. On remarque que si on sort le p et le k de la factorielle, on peut réécrire cela comme k-1 parmi p-1. Comme les coefficients binomiaux sont des nombres entiers, on peut en déduire que p divise k parmi p.
Ensuite, on veut montrer que a puissance p est congru à a modulo p en utilisant la récurrence sur a. On commence par l'initialisation en prenant a égale à 1, ce qui donne 1 puissance p congru à 1 modulo p.
Ensuite, on effectue l'étape de récurrence de a à a plus 1. Pour cela, on utilise la formule du binôme de Newton pour décomposer a plus 1 puissance p en une somme de coefficients binomiaux multipliés par a puissance k. On remarque que grâce à ce que l'on a montré précédemment, seul le terme correspondant à k égal à 0 et à k égal à p ne sont pas divisibles par p. En prenant la congruence modulo p, on peut simplifier cette somme pour obtenir a puissance p plus 1.
En utilisant l'hypothèse de récurrence, qui dit que a puissance p est congru à a modulo p, on peut conclure que a puissance p plus 1 est congru à a plus 1 modulo p. Ainsi, on a montré par récurrence que a puissance p est congru à a modulo p, ce qui est le petit théorème de Fermat.
Maths
Algèbre
MPSI/PCSI

Nombre de Fermat suite
Dans cet exercice, nous montrons qu'il y a une infinité de nombres premiers en utilisant les nombres de Fermat.
Nous commençons en montrant par récurrence que pour tout n et pour tout k plus grand que 1, nous avons l'égalité suivante : 2 puissance 2 puissance n plus k moins 1 est égal au produit de 2 puissance 2 puissance n moins 1 et du produit de 2 puissance 2 puissance n plus i plus 1 pour i allant de 0 à k moins 1.
Ensuite, nous montrons que pour tout m différent de n, les nombres de Fermat fn et fm sont premiers entre eux. Nous utilisons l'hypothèse de récurrence précédente pour montrer cela.
Enfin, nous utilisons les nombres de Fermat pour montrer qu'il y a une infinité de nombres premiers. Nous supposons qu'il existe un nombre fini de nombres premiers et nous considérons les nombres de Fermat F1, F2, F3, etc. jusqu'à FN plus 1. En utilisant le principe des tiroirs, nous montrons qu'il y a forcément deux nombres de Fermat distincts qui ont le même diviseur premier, ce qui contredit le fait qu'ils sont premiers entre eux. Par conséquent, il ne peut pas y avoir un nombre fini de nombres premiers et il en existe une infinité.
Maths
Algèbre
MPSI/PCSI

Ensemble de Nombre Premiers
Dans cet exercice, on cherche à démontrer qu'il existe une infinité de nombres premiers de la forme 4k + 3.
Tout d'abord, on doit prouver que l'ensemble x de ces nombres premiers est non vide. On remarque facilement que 3 est de la forme 4k + 3 avec k égal à 0, donc 3 appartient à x. Donc x est non vide.
Ensuite, on veut montrer que le produit de deux nombres de la forme 4k + 1 est également de cette forme. On prend donc deux nombres, k et l, et on effectue une multiplication. On factorise ensuite par 4 et on obtient un nombre k' qui peut s'écrire sous la forme 4k' + 1. Donc le produit de deux nombres de la forme 4k + 1 est bien de cette forme.
On suppose ensuite que l'ensemble x est fini, donc qu'il contient un nombre fini de nombres premiers de la forme 4k + 3, et on construit un nombre a égal à 4 multiplié par le produit de tous ces nombres, moins 1. On va montrer que a a nécessairement un diviseur premier de la forme 4k + 3.
On suppose par l'absurde que a n'a pas de diviseur premier de cette forme. On constate alors que tous les diviseurs de a doivent être de la forme 4k + 1. On exclut rapidement la possibilité que a soit divisible par 2, puisqu'il est impair. Donc tous ses diviseurs premiers doivent être de la forme 4k + 1.
Or, on a montré précédemment que le produit de nombres de la forme 4k + 1 est lui-même de cette forme. Mais a, qui est de la forme 4k - 1, ne correspond pas à cette propriété. Donc on aboutit à une contradiction et on prouve que a admet nécessairement un diviseur premier de la forme 4k + 3.
Cela signifie qu'il existe un nombre premier de la forme 4k + 3 qui divise a, contredisant ainsi l'hypothèse que l'ensemble x est fini. On conclut donc qu'il existe une infinité de nombres premiers de la forme 4k + 3.


