 All subjects
All subjects
 All subjects
All subjects
Corrigés de BAC
Bac Physique-Chimie
Terminale

La mission Grace-Fo (1)
Dans cette vidéo, Théobald de Studio explique la caractérisation de l'orbite d'un satellite dans le cadre de la mission GRAFO, qui envoie deux satellites jumeaux situés sur la même orbite. Il mentionne que l'attraction gravitationnelle de la planète varie faiblement d'un mois à l'autre en raison d'une infime fraction de la masse terrestre en mouvement. Dans la première partie de la vidéo, il se concentre sur la caractérisation de l'orbite des satellites de cette mission, qui est quasi-circulaire avec une altitude de 490 km et une inclinaison de 89° par rapport à l'équateur.
Il explique ensuite les forces qui s'appliquent sur les satellites. En se concentrant uniquement sur le mouvement d'un satellite, il présente le schéma de la Terre avec le satellite situé sur son orbite à une distance L de ce dernier. Il poursuit en donnant l'expression vectorielle de la force gravitationnelle exercée par la Terre sur le satellite, qui s'exprime par G * masse de la Terre * masse du satellite / distance Terre-satellite au carré, portée par un vecteur unitaire dirigé du satellite vers la Terre.
Il en déduit ensuite l'expression du champ vectoriel terrestre, qui est égal à G * masse de la Terre * masse du satellite / (rayon de la Terre + altitude du satellite) au carré, porté par le vecteur unitaire dirigé du satellite vers la Terre.
En considérant uniquement l'action de la Terre, il établit l'expression vectorielle de l'accélération du satellite en utilisant le principe fondamental de la dynamique. Il obtient que l'accélération du satellite est égale au champ gravitationnel terrestre.
Il montre ensuite que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Il explique que dans un mouvement circulaire, l'accélération peut être décomposée en une composante tangentielle et une composante normale. En utilisant cette décomposition, il démontre que l'accélération tangentielle est nulle, ce qui signifie que la vitesse du satellite est constante et donc que son mouvement est circulaire uniforme.
Il conclut cette partie de la vidéo en invitant les spectateurs à poser leurs questions en commentaire.
Corrigés de BAC
Bac Physique-Chimie
Terminale

La mission Grace-Fo (2)
Dans ce cours, nous étudions le mouvement d'un satellite autour de la Terre. Nous démontrons que la vitesse du satellite peut être exprimée par la relation GMt/RT+Z. Nous calculons ensuite la période de révolution du satellite, qui est d'environ 1h34. En utilisant cette période, nous déterminons que le satellite fait environ 15 tours de la Terre en une journée.
Ensuite, nous étudions deux satellites, où le premier passe au-dessus d'une zone où le champ gravitationnel n'est pas centripète, contrairement au deuxième satellite. Nous démontrons que la distance entre les deux satellites augmente, car le deuxième satellite est soumis à un mouvement circulaire uniforme, tandis que le premier subit un mouvement circulaire accéléré. En conséquence, la distance entre les deux satellites augmente.
Corrigés de BAC
Bac Physique-Chimie
Terminale

La mission Grace-Fo (3)
Dans cette vidéo, Théobald de Studio explique le principe de l'interféromètre embarqué utilisé dans la mission GRASFO. Deux satellites jumeaux sont envoyés sur la même orbite pour mesurer leur distance et analyser les variations du champ gravitationnel autour de la Terre. L'interféromètre fonctionne en envoyant un laser sur un miroir semi-réfléchissant. Les interférences observées permettent de calculer la distance entre les deux satellites. La cohérence des sources est assurée par le miroir semi-réfléchissant, qui sépare le faisceau laser en deux. La différence de marche, qui correspond à la différence de distance parcourue par les deux faisceaux, peut être calculée à partir du schéma du dispositif. La variation de la différence de marche, delta d, est égale à 2d lorsque le satellite 1 s'éloigne du satellite 2. La détectabilité maximale du détecteur d'interférence correspond à une variation de différence de marche égale à λ/2, où λ est la longueur d'onde de la lumière utilisée. Ainsi, la plus petite variation de distance détectable par l'interféromètre est de 532 nanomètres.
Corrigés de BAC
Bac Physique-Chimie
Terminale

La mission Grace-Fo (4)
Dans cette vidéo, Théobald de Studio explique le fonctionnement d'un accéléromètre utilisé dans le cadre d'une mission de Grasse-Faux pour mesurer le champ gravitationnel terrestre. L'accéléromètre utilise une masse d'épreuve placée au centre d'une cage électrostatique qui subit un déplacement en réponse à une force non gravitationnelle. Ce déplacement modifie la capacité des condensateurs du dispositif. L'étude se concentre sur un condensateur plan dont l'armature mobile est constituée par la face gauche de la masse d'épreuve. En l'absence de force non gravitationnelle, la capacité du condensateur est définie par la formule C = Y0S / (E + X), où Y0 est la permittivité électrique du vide, S est la surface en regard des armatures, E est la distance entre les armatures et X est le déplacement de la masse mobile. On observe donc une relation inverse entre le déplacement X et la capacité C. En ce qui concerne le champ électrique, il est déterminé par E = U / (E + X), où U est la tension appliquée entre les armatures du condensateur plan. L'armature mobile est soumise au champ E1 créé par l'armature fixe, et les lois de l'électrostatique montrent que E1 = E / 2. Ainsi, l'armature mobile subit une force F opposée à E. Parmi les quatre schémas donnés, le schéma 2 correspond à la représentation correcte du champ électrique E et de la force électrique F. Enfin, dans un dernier exercice, on nous présente un dispositif où la masse d'épreuve est mobile entre deux armatures fixes opposées. Les forces électrostatiques exercées par les armatures fixes se compensent, ce qui conduit à l'égalité des champs électriques à droite et à gauche, soit ED = EG.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Protection des fondations en acier des éoliennes en mer (1)
Dans cette vidéo, Théobald de Studio parle de la protection des éoliennes en mer contre la corrosion. Il explique qu'il y a deux principales méthodes de protection : l'utilisation d'une anode sacrificielle en aluminium, qui corrode à la place du fer, ou l'utilisation d'une protection par courant imposé. L'exercice se concentre sur la protection cathodique avec une anode sacrificielle en aluminium.
L'objectif de l'exercice est de vérifier si, en milieu oxydant, le fer peut être protégé de l'oxydation en étant en contact électrique avec de l'aluminium. Pour cela, une expérience est réalisée : une plaque d'aluminium est mise en contact avec une solution de sulfate d'aluminium, et une plaque de fer est mise en contact avec une solution de chlorure de fer. Les deux plaques sont reliées par un fil électrique pour former une pile.
On demande ensuite d'exprimer le quotient de réaction initial associé à cette réaction. Le quotient de réaction est calculé en utilisant les concentrations des ions Al3+ et Fe2+ et les coefficients stoichiométriques de la réaction.
La valeur du quotient de réaction initiale est calculée et comparée à la constante d'équilibre de la réaction. Si le quotient de réaction est inférieur à la constante d'équilibre, la réaction se fait dans le sens direct. Dans ce cas, la réaction va se faire dans le sens direct.
En utilisant les résultats précédents, Théobald déduit la réaction qui se passe à l'électrode d'aluminium. Il explique que l'aluminium solide réagit pour former des ions Al3+ et des électrons, ce qui est cohérent avec les observations expérimentales.
Ensuite, l'électrode qui joue le rôle de l'anode dans la pile est identifiée comme étant l'électrode d'aluminium, car elle subit une oxydation en cédant des électrons.
La prochaine vidéo abordera le sujet de la protection de l'éolienne et de la quantité d'aluminium nécessaire. Théobald encourage les spectateurs à poser des questions dans les commentaires.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Protection des fondations en acier des éoliennes en mer (2)
Dans cette vidéo, Oval2Studio explique comment calculer la masse d'aluminium nécessaire pour protéger complètement les éoliennes en air. Il est expliqué que l'aluminium réagit préférentiellement avec le dioxygène dissous dans l'eau, ce qui en fait le matériau idéal pour la protection cathodique des éoliennes. L'équation de réaction chimique entre l'aluminium et le dioxygène dissous est présentée, ainsi que les demi-équations correspondantes à chaque couple redox. En égalisant le nombre d'électrons échangés dans chaque demi-équation, on peut ensuite obtenir l'équation de réaction finale.
Ensuite, il est mentionné qu'une protection efficace correspond à un courant électrique d'intensité de 400 A. Pour calculer la masse d'aluminium nécessaire pour une durée de 25 ans, on utilise la relation entre l'intensité du courant électrique et la capacité électrique de la pile. On sait que pour chaque capacité électrique, on échange deux électrons, ce qui permet de relier le nombre d'électrons à la quantité de matière d'aluminium. En utilisant la masse molaire de l'aluminium, on peut alors calculer la masse d'aluminium nécessaire.
Le résultat numérique obtenu est de 2,9 x 10^4 kilogrammes d'aluminium, ce qui représente une quantité énorme. Cependant, le constructeur a choisi une autre solution pour la protection des éoliennes, en raison des coûts élevés associés à une telle quantité d'aluminium, ainsi que de l'impact environnemental de la libération d'ions aluminium dans la mer.
En conclusion, ce cours explique comment déterminer la masse d'aluminium nécessaire pour protéger les éoliennes en air, et présente les raisons pour lesquelles le constructeur a choisi une solution alternative.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Additif alimentaire pour les agneaux (1)
Dans cette vidéo, on se focalise sur un exercice de chimie ayant pour sujet le titrage par suivi conductimétrique. Cet exercice concerne les additifs alimentaires pour les agneaux, notamment le chlorure d'ammonium utilisé pour prévenir les maladies liées à la consommation excessive de céréales et de protéagineux.
Dans cet exercice, un éleveur administre quotidiennement un litre d'une solution de chlorure d'ammonium à un agneau de 24 kg, préparée par ses soins. L'objectif est de vérifier si la préparation de l'éleveur est conforme aux recommandations du site des partenaires de la production aux villes en France.
Un titrage conductimétrique est effectué en utilisant 10,00 ml de la solution préparée par l'éleveur diluée avec un volume d'eau distillée. La solution titrante utilisée est de l'hydroxyde de sodium (NaOH). La réaction chimique impliquée est celle entre le chlorure d'ammonium (NH4+) et l'hydroxyde de sodium (NaOH), qui donne de l'ammoniac (NH3) et de l'eau (H2O). Cette réaction est classée comme une réaction acido-basique étant donné l'échange de protons (H+) entre les réactifs.
En ce qui concerne le dispositif de titrage conductimétrique, un schéma est proposé avec une béchamel contenant la solution titrée, une burette graduée contenant la solution titrante, une sonde reliée à un conductimètre, et une autre sonde attachée à une potence avec un agitateur magnétique. Il est indiqué que le volume à l'équivalence est d'environ 14 mL, qui est déterminé en traçant la courbe conductimétrique obtenue à la fin du titrage.
Pour calculer la concentration en quantité de matière de la solution préparée par l'éleveur, il est utilisé l'équation de titration. Étant donné que les réactifs sont introduits en proportion stoichiométrique à l'équivalence, le nombre de moles de chlorure d'ammonium (NH4+) est égal au nombre de moles de l'hydroxyde de sodium (NaOH) à l'équivalence. En utilisant les concentrations et les volumes associés, l'expression de la concentration est trouvée. Il est précisé que la dilution de la solution titrée ne change rien et ne doit pas être prise en compte dans les calculs.
Ensuite, l'incertitude de la concentration obtenue est discutée. Il est proposé d'encadrer la concentration de la solution préparée par l'éleveur en utilisant les valeurs d'incertitude absolue données pour différents instruments de mesure (burette, pipette jaugée, éprouvette graduée). Étant donné la précision et la précision de mesure du volume VA (10,00 ml), il est conclu qu'une pipette jaugée a probablement été utilisée pour prélever ce volume. L'incertitude absolue sur ce volume est calculée et utilisée pour déterminer l'incertitude absolue sur la concentration.
Enfin, il est demandé de calculer la masse de chlorure d'ammonium donnée quotidiennement à l'agneau par l'éleveur et de comparer ce résultat à la valeur préconisée par le site des partenaires de la production aux villes en France. En utilisant la quantité de matière, la masse molaire et le volume (1 L) donnés, la masse est calculée. Il est constaté que la masse (7,5 g) est conforme à l'intervalle de valeurs préconisé par le site pour un agneau de 24 kg.
Pour toute question, il est invité à les poser en commentaire et le contenu se termine en annonçant une prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
Terminale

Additif alimentaire pour les agneaux (2)
Dans cette vidéo, Théobald de Studio parle du code Python nécessaire pour simuler un titrage par conductimétrie. Il explique qu'il s'agit d'un exercice dans lequel un éleveur donne des compléments alimentaires à son agneau et on veut vérifier si ces compléments sont cohérents. On effectue donc un titrage pour évaluer la concentration de la solution donnée à l'agneau.
La première question consiste à compléter le code à écrire aux lignes 6, 7 et 8, qui correspondent aux nombres stoichiométriques des espèces. A, B et C représentent respectivement les nombres stoichiométriques de NH4+, HO- et NH3+. Puisqu'ils sont tous égaux à 1 dans l'équation de réaction, on les définit tous comme 1.
Ensuite, on demande d'identifier les deux espèces chimiques correspondantes aux variables NSA et NSB. On constate que NSA est égal à la quantité de matière initiale de NH4+ ou de Cl-, alors que NSB est égal à la quantité de matière de Na+ versé dans la solution. Cela signifie que NSA représente la quantité de matière de Cl- et NSB représente la quantité de matière de Na+ en cours de réaction.
On nous présente ensuite cinq graphiques représentant l'évolution de la quantité de matière des différentes espèces chimiques en fonction du volume de solution titrante versé. Pour déterminer quel graphique correspond à quelle espèce chimique, on utilise un tableau de présence des espèces chimiques avant et après l'équivalence. On observe que la concentration de HO- augmente avant l'équivalence, que la quantité de matière de NH4+ diminue, que la quantité de matière de Na+ augmente, que la quantité de matière de Cl- reste constante et que la quantité de matière de NH3 augmente et reste constante après l'équivalence. On peut donc attribuer chaque graphique à l'espèce chimique correspondante.
Enfin, on nous demande de compléter le code aux lignes 12 et 19. À la ligne 12, on cherche le volume à l'équivalence en utilisant la formule CAVA/CB. À la ligne 19, on calcule Nb en utilisant la formule CAVA-CBVB. On conclut que A représente NH4+ et B représente HO-.
C'est ainsi que se termine cet exercice. N'hésitez pas à poser vos questions en commentaire et à attendre la prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
Terminale
Analyse d’un pigment à base d’oxyde de fer (1)
Dans cette vidéo, nous nous intéressons à l'analyse d'un pigment à base d'oxyde de fer. Un pigment est une espèce chimique colorante et insoluble dans le milieu qu'elle colore. Dans cet exercice, nous analysons une poudre colorante contenant un pigment d'oxyde de fer de formule Fe2O3.
Le fabricant indique que la teneur en oxyde de fer de cette poudre est de 5%. Nous allons donc réaliser une analyse quantitative de ce produit en utilisant un dosage par étalonnage.
Dans la première étape, nous préparons une gamme d'étalons contenant des ions fer 3. Nous réalisons ensuite une courbe d'étalonnage à partir des mesures spectrophotométriques sur des solutions de concentration connue. Enfin, nous effectuons la préparation et l'analyse de l'échantillon.
Dans la partie A de l'exercice, nous préparons une gamme d'étalons à partir de la solution mère S0, qui contient les ions fer 3 en milieu acide à une concentration de 25,0 mg par litre. Pour cela, nous dissolvons du chlorure de fer 3 exahydraté solide de formule FECL3-6H2O. L'équation de dissolution de ce chlorure de fer 3 exahydraté est la suivante : FECL3-6H2O → FE3+ + 3CL- + 6H2O.
Pour déterminer la masse de soluté nécessaire à l'obtention de la solution S0, nous utilisons la quantité de matière en ion fer 3. Cette quantité de matière est égale à la concentration massique multipliée par le volume de la solution, divisée par la masse molaire des ions fer 3.
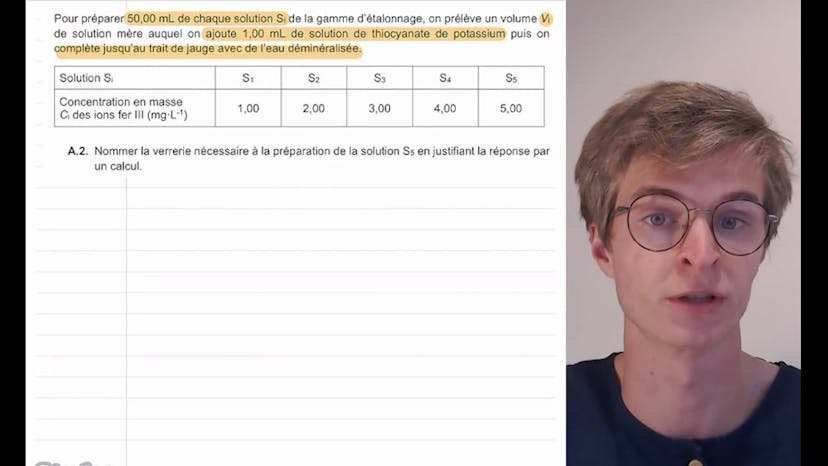
Dans la partie B de l'exercice, nous préparons différentes solutions SI de la gamme d'étalonnage en diluant la solution mère avec de l'eau déminéralisée et en ajoutant de la solution de thiocyanate de potassium. La masse de solution mère à prélever pour la préparation de la solution S5 est calculée en utilisant la conservation de la quantité de matière et de la masse lors d'une dilution.
Dans la partie C de l'exercice, nous réalisons un spectre d'absorption d'une solution de fer 3 en présence de thiocyanate. La couleur de la solution est déterminée en trouvant la longueur d'onde du maximum d'absorption et en prenant la couleur complémentaire. La longueur d'onde lambda0 la plus adaptée pour effectuer les mesures d'absorbance est également indiquée.
Si vous avez des questions, n'hésitez pas à les poser en commentaire et nous y répondrons avec plaisir.
Corrigés de BAC
Bac Physique-Chimie
Terminale
Analyse d’un pigment à base d’oxyde de fer (2)
Dans cette vidéo, Théobald de Cidéo aborde l'analyse d'un pigment à base d'oxyde de fer. Le pigment a une espèce chimique colorante insoluble dans le milieu qu'elle colore. L'objectif est de vérifier la teneur en oxyde de fer annoncée par le fabricant, qui affirme que la poudre contient 5% d'oxyde de fer.
La première partie de l'exercice consiste en la préparation d'une gamme étalon contenant des ions de fer. Ensuite, une courbe d'étalonnage est réalisée à l'aide de mesures spectrophotométriques pour établir la relation entre l'absorbance et la concentration molaire. Cette courbe d'étalonnage est compatible avec la loi de Berlembert, selon laquelle l'absorbance est proportionnelle à la concentration.
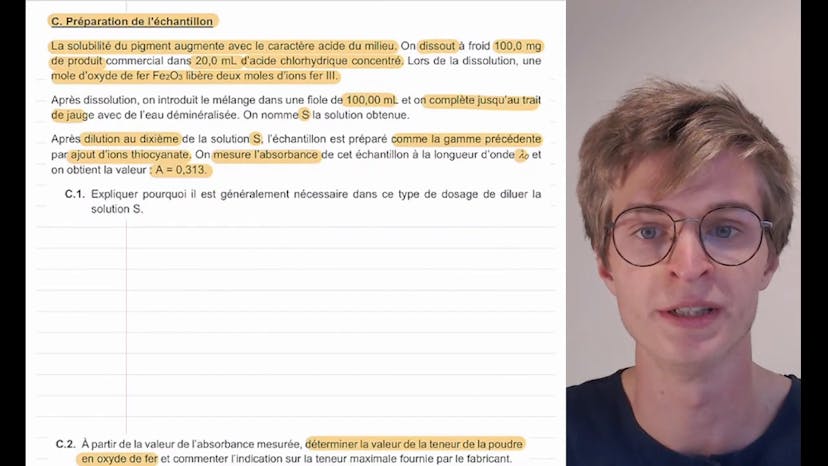
La deuxième partie de l'exercice concerne la préparation de l'échantillon. Il est mentionné que la solubilité du pigment augmente avec le caractère acide du milieu. Ainsi, 100 mg de produit sont dissous à froid dans 20 mg d'acide chlorhydrique concentré pour augmenter la solubilité du pigment. Le mélange est ensuite dilué et une fiole de 100 mg est complétée avec de l'eau déminéralisée. La solution obtenue est notée S.
Dans la troisième partie de l'exercice, la solution S est diluée au dixième pour préparer l'échantillon. L'absorbance de l'échantillon est mesurée à la longueur d'onde lambda0, et on obtient une valeur de 0,313.
Il est expliqué que la dilution de la solution S est nécessaire car la loi de Berlembert s'applique généralement aux solutions diluées. En utilisant la relation entre l'absorbance et la concentration massique en fer, la valeur de la teneur en oxyde de fer dans la poudre peut être déterminée. Le calcul est effectué en remontant les étapes : concentration massique en fer 3 dans l'échantillon, concentration massique en fer 3 dans la solution S, quantité d'ion fer dans la solution S, quantité de matière en oxyde de fer, et enfin la teneur en oxyde de fer dans la poudre.
Après les calculs, il est conclu que la teneur en oxyde de fer de la poudre est de 5,1%, ce qui est conforme à l'annonce du fabricant qui indiquait une teneur de 5%.
Cet exercice permet de comprendre comment réaliser un dosage par étalonnage et de vérifier les assertions d'un fabricant en utilisant des mesures spectrophotométriques.
Corrigés de BAC
Bac Physique-Chimie
Terminale

La vitamine C sans sucre (1)
Dans cette vidéo, Théobald de Cidéo explique comment déterminer le spectre infrarouge de l'aspartame, une molécule que l'on retrouve dans la vitamine C. Il commence par donner des informations sur la vitamine C et sur l'aspartame, qui est un édulcorant de synthèse utilisé dans de nombreux produits.
Ensuite, il aborde les différentes familles fonctionnelles présentes dans la formule topologique de l'aspartame. Il montre que l'aspartame contient un acide carboxylique, un amine et un ester, et explique l'importance de ces groupes pour l'analyse du spectre infrarouge.
Il explique ensuite que l'aspartame peut être synthétisé à partir de l'acide aspartique, et demande de représenter la formule semi-développée de cet acide. Il souligne l'importance de respecter la géométrie de la molécule et de dessiner les liaisons entre les bons éléments.
Enfin, il présente les spectres obtenus par spectroscopie infrarouge de l'aspartame et de l'acide aspartique, sans préciser à quel spectre correspond quelle molécule. Il explique les bandes caractéristiques qui devraient ressortir dans le spectre infrarouge de l'aspartame, en se basant sur les différentes familles fonctionnelles présentes.
Il analyse ensuite les spectres infrarouges des deux molécules et conclut que le spectre 2 correspond au spectre de l'aspartame, car il présente toutes les bandes caractéristiques attendues.
Enfin, il termine en invitant les spectateurs à poser des questions en commentaire et annonce une prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
Terminale
La vitamine C sans sucre (2)
Dans cette vidéo, Théobald de Studio aborde le sujet de l'aspartame et sa synthèse. Il explique que l'aspartame est une molécule présente dans la vitamine C et qu'il souhaite montrer comment la synthétiser.
Il commence par présenter le contexte de l'exercice, qui tourne autour de la vitamine C et de l'acide ascorbique qui la compose. Il mentionne également que la synthèse de l'aspartame nécessite plusieurs étapes, mais qu'il se concentrera sur l'une des premières étapes consistant à transformer une espèce chimique A en une espèce chimique C.
Il explique ensuite qu'il y a trois protocoles expérimentaux, notés 1, 2 et 3, qui sont réalisés à la même température. Ces protocoles varient en termes de masses des réactifs, de rendements, etc.
La première question de l'exercice demande de déterminer le volume de réactif B liquide à prélever dans le protocole 1. Théobald explique qu'il peut utiliser la quantité de matière du réactif B (NB) donnée dans l'énoncé pour calculer le volume correspondant. Il utilise la formule du volume (massse/masse volumique) pour obtenir le résultat, qui est de 1,0 millilitre.
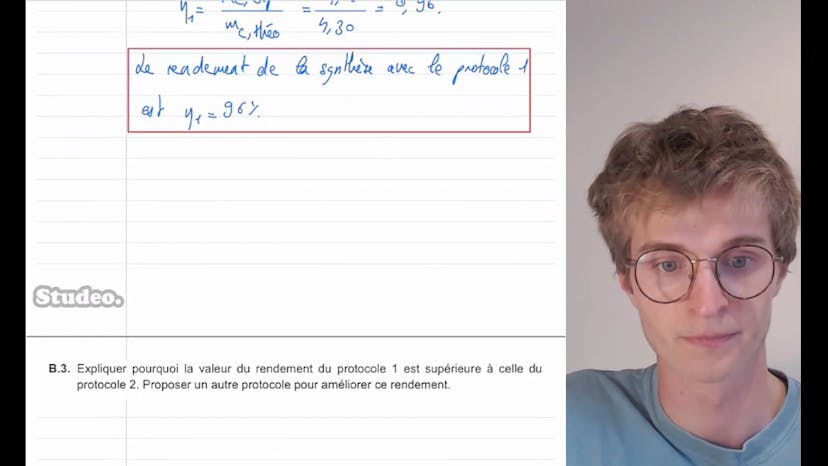
Ensuite, il est demandé de calculer le rendement de la synthèse dans le protocole 1. Théobald explique que le rendement est défini comme la masse du produit C obtenue expérimentalement divisée par la masse théorique maximale du produit. Il utilise les données expérimentales pour obtenir la masse théorique en supposant une réaction totale. Il obtient un résultat de 4,30 grammes de produit C théoriquement obtenu. En comparant cela avec la masse expérimentale de 4,12 grammes, il calcule un rendement de 96% dans le protocole 1.
On lui demande ensuite d'expliquer pourquoi le rendement du protocole 1 est supérieur à celui du protocole 2. Théobald remarque que la seule différence entre les deux protocoles est la quantité de matière en réactif A, qui est plus élevée dans le protocole 1. Il explique que cela signifie que A est en excès dans le protocole 1, ce qui permet d'obtenir un rendement plus élevé. Il suggère également que l'élimination d'un des produits, comme l'eau, pourrait améliorer le rendement.
En utilisant les informations du tableau, Théobald identifie ensuite le rôle du palladium sur carbone. Il remarque que sa présence dans les deux premières réactions raccourcit la durée de réaction, ce qui indique que le palladium sur carbone agit comme un catalyseur, accélérant la réaction.
En conclusion, Théobald résume les résultats obtenus dans cette vidéo et annonce qu'il abordera la partie C de l'exercice dans une prochaine vidéo. Il encourage les spectateurs à poser leurs questions dans les commentaires.
Corrigés de BAC
Bac Physique-Chimie
Terminale

La vitamine C sans sucre (3)
Dans cette vidéo, Théobald de Cidéo explique l'acide ascorbique, qui est le nom scientifique de la vitamine C. Il aborde un exercice du BAC portant sur l'acide ascorbique. Dans cet exercice, il est demandé de calculer la concentration en quantité de matière de l'acide ascorbique dans une solution obtenue en dissolvant un comprimé de 0,50 g d'acide ascorbique dans 200,0 ml d'eau. Théobald utilise la formule de concentration en quantité de matière qui est le nombre de moles divisé par le volume de la solution. Il calcule ensuite la concentration en quantité de matière de l'acide ascorbique, qui est de 1,4 x 10^-2 mol/L, correspondant à la réponse B.
Ensuite, Théobald explique comment écrire l'équation de réaction entre l'acide ascorbique et l'eau, en soulignant que l'acide ascorbique est un acide faible. Il présente les couples d'espèces présentes dans la réaction, et montre que la réaction se produit entre l'acide ascorbique et l'eau pour former l'ion ascorbate et l'ion H3O+. Il mentionne également que le pH à l'équilibre de la solution est de 2,9.
Théobald aborde ensuite le calcul de la constante d'acidité Ka, en montrant comment caractériser l'équilibre à l'aide d'un tableau d'avancement. Il utilise les concentrations en ion aspartame et en ion H3O+ pour déterminer la valeur de Ka, qui peut s'écrire selon la formule donnée dans l'énoncé.
L'étape suivante consiste à trouver la valeur de Ka et le pKa du couple acide ascorbique-ion ascorbate. Théobald substitue la concentration en ion H3O+ par C standard multipliée par 10^-pH dans la formule de Ka, et obtient une valeur de Ka égale à 1,2 x 10^-4. Il calcule ensuite le pKa, qui est égal à 3,9.
Enfin, Théobald représente le diagramme de prédominance du couple ascorbique-ion ascorbate en fonction du pH. Il indique que la forme majoritaire dans l'estomac, où le pH est d'environ 2, est l'acide ascorbique, car l'acide prédomine à pH faible. Il conclut la vidéo en souhaitant bonne chance dans les révisions et en proposant de poser des questions en commentaire.
Corrigés de BAC
Bac Physique-Chimie
Terminale

La vitamine C sans sucre (4)
Dans cette vidéo, Théoval de Cedéo aborde le sujet de la détermination de la masse d'acide ascorbique contenu dans un comprimé de vitamine C. Le fabricant indique que chaque comprimé contient 500mg de vitamine C, uniquement sous forme d'acide ascorbique. L'objectif est de vérifier cette information en utilisant une méthode de titrage conductimétrique.
Le processus expérimental consiste à dissoudre un comprimé de vitamine C dans de l'eau distillée pour obtenir une solution d'un volume de 250mL. Ensuite, un échantillon de 40mL de cette solution est titré à l'aide d'une solution d'hydroxyde de sodium de concentration connue. L'équation de réaction du titrage est donnée, où l'acide ascorbique réagit avec les ions hydroxyde.
Le dispositif expérimental est simple : un bécher contenant la solution titrée avec une sonde de conductimétrie reliée à un conductimètre et une burette graduée contenant la solution d'hydroxyde de sodium.
Les courbes d'évolution de la conductivité du milieu réactionnel en fonction du volume d'hydroxyde de sodium versé sont données. On observe une augmentation de la conductivité avec l'augmentation du volume ajouté, avec deux demi-droites tracées.
Pour expliquer cette évolution, il est nécessaire de comprendre la présence des ions dans la solution. Avant l'équivalence, les ions hydroxyde réagissent avec l'acide ascorbique, tandis que les ions sodium restent inchangés. Après l'équivalence, les ions hydroxyde sont ajoutés mais ne réagissent plus avec l'acide ascorbique, tandis que les ions sodium restent inchangés. Cette évolution explique l'augmentation de la conductivité avant et après l'équivalence.
La concentration molaire d'acide ascorbique de la solution titrée est déterminée en utilisant le principe de l'équivalence. Le volume à l'équivalence est trouvé à partir de l'intersection des deux demi-droites tracées sur la courbe. En utilisant cette concentration et le volume de la solution S, la quantité de matière d'acide ascorbique est calculée et convertie en masse.
La masse d'acide ascorbique contenue dans un comprimé est trouvée être de 0,19g. En comparant cette valeur à celle annoncée par le fabricant (200mg), on calcule le rapport entre la valeur mesurée et la valeur de référence. Ce rapport, également appelé z-score, est égal à 1, ce qui indique que la mesure est compatible avec la valeur de référence.
En conclusion, la méthode de titrage conductimétrique a permis de déterminer avec précision la masse d'acide ascorbique dans un comprimé de vitamine C, et cette valeur est cohérente avec celle annoncée par le fabricant.
Corrigés de BAC
Bac Physique-Chimie
Terminale
La pente d'eau de Montech (1)
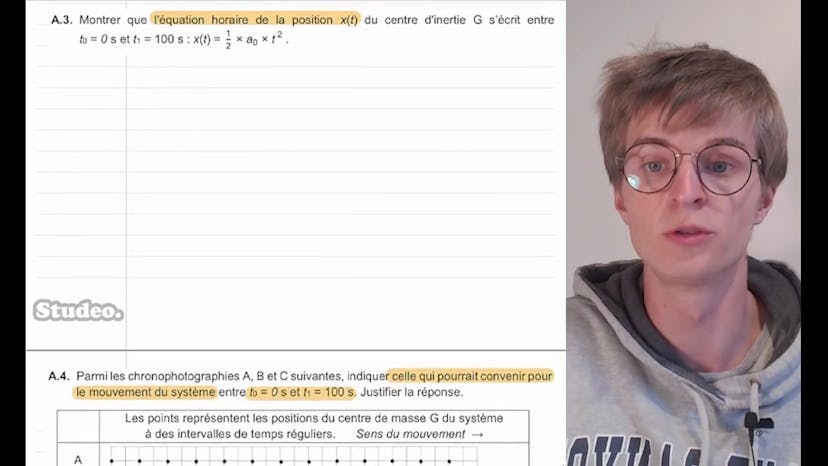
Avoir un ascenseur à bateau est très avantageux pour monter ou descendre les bateaux rapidement. L'ascenseur à bateau de Montaigue est un exemple de cela. Il est devenu un site touristique depuis 2021. Le principe de fonctionnement de cet ascenseur à bateau est expliqué ici. Il utilise une automotrice pour pousser le masque, le bateau et l'eau qui est entre les deux, permettant ainsi au système de monter la pente. Dans cette première partie, nous étudions le mouvement de ce système. Le centre de masse G se déplace selon l'axe OX avec un angle α par rapport à l'horizontale. À l'instant initial t=0, le centre de masse est au point O. Nous utilisons une chronophotographie pour représenter ce mouvement. On nous demande de donner la relation entre l'accélération et la vitesse, et de déduire la relation entre leurs valeurs absolues. La relation entre l'accélération A de t et la vitesse V de t est donnée par la dérivée de la vitesse par rapport au temps. En raison du mouvement rectiligne, nous pouvons exprimer l'accélération et la vitesse en termes de leurs valeurs absolues. Donc, A de t est égal à la dérivée de la vitesse par rapport au temps. Nous devons ensuite montrer que l'accélération du système est constante entre t=0 et t1=100 secondes, et qu'elle vaut A0=1,20 fois 10 à la puissance -2 m/s². En analysant la courbe, nous pouvons voir que l'accélération est constante dans cette période. En utilisant la relation delta V/delta t, nous pouvons calculer la valeur de l'accélération. Delta V est égal à V(t1) - V(t0) et delta t est égal à t1 - t0. En utilisant les conditions initiales V(t0) = 0 et t0 = 0, nous obtenons A0 = 1,20 fois 10 à la puissance -2 m/s², la valeur donnée dans l'énoncé. Ensuite, nous devons trouver l'équation de la vitesse et de la position du centre de masse du système en fonction de A0 et de t pour cette partie du mouvement. En intégrant l'accélération, nous obtenons la vitesse, V(t) = A0t. En intégrant à nouveau la vitesse, nous obtenons la position du centre de masse, x(t) = 1,5A0t². Entre t=0 et t1=100 secondes, la vitesse est une ligne droite et la position est une courbe parabolique. Enfin, en utilisant des chronophotographies, nous devons déterminer quelle représentation du mouvement correspond à notre système entre t0 et t1. En utilisant les équations précédentes, nous pouvons calculer les positions des points à différents intervalles de temps. En comparant ces positions avec celles des chronophotographies A, B et C, nous pouvons déterminer laquelle correspond à notre mouvement. La chronophotographie B correspond à notre mouvement car les distances entre les points sont régulières pour des intervalles de temps réguliers, ce qui correspond à une accélération constante.
Corrigés de BAC
Bac Physique-Chimie
Terminale

La pente d'eau de Montech (2)
Dans cette vidéo, Théobald poursuit l'exercice sur l'ascenseur à bateau. Dans la première partie, il étudie la dynamique du système, tandis que dans la deuxième partie, il utilise une lunette pour observer le bateau.
Le système étudié est composé du bateau, de l'eau et du masque. Le bateau se déplace le long de la pente et est soumis à quatre forces : son poids, la réaction normale de la pente, les forces automotrices et la force de frottement du masque et de l'eau le long de la pente. Les forces automotrices permettent au bateau de remonter la pente. Théobald explique que la somme des forces extérieures doit être selon le sens de l'accélération du système, qui est positif selon l'axe plus ux. Il analyse ensuite deux schémas pour déterminer lequel représente le mieux la situation. Il conclut que le schéma 1 est le plus approprié, car la somme des
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La mission Grace-Fo (1)
Dans cette vidéo, Théobald de Studio explique la caractérisation de l'orbite d'un satellite, en se basant sur la mission GRAFO qui envoie deux satellites jumeaux sur la même orbite. Il mentionne que l'attraction gravitationnelle de la planète varie faiblement d'un mois à l'autre en raison d'une infime fraction de la masse terrestre en mouvement constant, ce qui entraîne des variations dans l'attraction gravitationnelle.
Dans la première partie de la vidéo, Théobald se concentre sur la caractérisation de l'orbite des satellites. Il explique que l'orbite est quasi-circulaire, avec une altitude z de 490 km et une inclinaison de 89° par rapport à l'équateur. Il mentionne également que les satellites sont situés à une distance L l'un de l'autre. Il présente ensuite les forces qui s'appliquent sur les satellites, en se concentrant sur le mouvement d'un seul satellite pour l'instant.
Dans une question, il demande de faire un schéma montrant la Terre, le rayon RT et le satellite situé sur son orbite à une altitude z. Il explique ensuite l'expression vectorielle de la force gravitationnelle F de T sur S exercée par la Terre sur le satellite. Il utilise une formule qui comprend la masse de la Terre, la masse du satellite et la distance entre la Terre et le satellite. Il conclut que la force gravitationnelle est attractive et doit être dirigée vers la Terre.
Ensuite, il demande d'en déduire l'expression du champ vectoriel terrestre G. Il utilise la relation entre la force gravitationnelle et le champ gravitationnel pour trouver cette expression.
Dans une autre question, il demande d'établir l'expression vectorielle de l'accélération a du satellite en considérant uniquement l'action de la Terre. Il utilise le principe fondamental de la dynamique pour trouver cette expression.
Enfin, il demande de montrer que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Il suppose l'orbite circulaire et explique que dans ce cas, le mouvement est uniforme si la vitesse est constante. Il décompose l'accélération en accélération tangentielle et accélération normale et utilise cette décomposition pour montrer que la vitesse est constante dans le cas d'un mouvement circulaire.
La vidéo se termine ici, mais Théobald encourage les spectateurs à poser des questions dans les commentaires.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La mission Grace-Fo (1)
Dans cette vidéo, Théobald de Studio aborde la caractérisation de l'orbite d'un satellite dans le cadre de la mission GRAFO. Il explique que cette mission envoie deux satellites jumeaux sur la même orbite. L'attraction gravitationnelle de la planète varie légèrement d'un mois à l'autre en raison d'une fraction infime de la masse terrestre constamment en mouvement. Cela peut rendre l'attraction gravitationnelle tantôt centripète, tantôt non centrée.
Dans la première partie de la vidéo, Théobald se concentre sur la caractérisation de l'orbite. Il mentionne que l'orbite des satellites de cette mission est quasi-circulaire, à une altitude de 490 km et avec une inclinaison de 89° par rapport à l'équateur. Il note également que les deux satellites sont situés à une distance l l'un de l'autre.
Il explique ensuite les forces qui s'appliquent aux satellites, en se concentrant sur le mouvement d'un seul satellite pour l'instant. On lui demande de faire un schéma montrant la Terre, le rayon RT et le satellite situé sur son orbite à une altitude z. Il indique que la force gravitationnelle exercée par la Terre sur le satellite peut être représentée par le vecteur n dirigé du satellite vers la Terre. Il donne ensuite l'expression vectorielle de cette force, qui dépend de la masse de la Terre, de la masse du satellite et de la distance entre la Terre et le satellite, portée par le vecteur n. Il rappelle que cette force est attractive et donc dirigée dans le sens de n.
Il poursuit en déduisant l'expression du champ gravitationnel terrestre, puisque la force gravitationnelle et le champ gravitationnel sont reliés. Cette expression dépend de la masse de la Terre, de la masse du satellite, de la distance entre la Terre et le satellite et est portée par le vecteur n.
Ensuite, Théobald établit l'expression vectorielle de l'accélération du satellite en considérant uniquement l'action de la Terre. Il définit le système comme étant le satellite de masse m et de centre de masse S, et le référentiel comme étant géocentrique supposé galiléen. Utilisant le principe fondamental de la dynamique, il montre que la somme des forces extérieures est égale à la masse du satellite multipliée par son accélération. En utilisant l'expression de la force gravitationnelle précédemment calculée, il trouve l'expression de l'accélération du satellite, qui dépend du champ gravitationnel, de la masse du satellite, de la distance entre la Terre et le satellite et est portée par le vecteur n.
Enfin, il montre que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Pour cela, il suppose que l'orbite est circulaire et montre que si c'est le cas, le mouvement du satellite est uniforme, ce qui signifie que sa vitesse est constante. Il utilise la décomposition de l'accélération en accélération tangentielle et accélération normale pour montrer que dans ce cas, l'accélération du satellite est uniquement selon le vecteur unitaire n. Cela signifie que le terme de la dérivée de la vitesse par rapport au temps est nul, ce qui entraîne que la vitesse du satellite est constante et donc que son mouvement est uniforme.
Théobald conclut cette première partie de l'exercice et invite les spectateurs à poser des questions en commentaire.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La mission Grace-Fo (2)
Dans cette vidéo, Théobald de Sudéo poursuit l'étude du mouvement d'un satellite autour de la Terre. Il rappelle que dans la vidéo précédente, ils ont étudié le mouvement circulaire uniforme du satellite sur une orbite circulaire. Maintenant, ils doivent montrer que l'expression de la vitesse du satellite peut être exprimée comme GMt divisé par RT plus Z.
Théobald explique qu'ils ont l'expression de l'accélération du satellite, qui comprend GMt divisé par RT plus Z, où G est la masse de la Terre et RT est le rayon de la Terre. Il souligne également que dans un mouvement circulaire uniforme, l'accélération est uniquement portée par le vecteur normal, qui est dirigé vers le centre de la Terre. Il n'y a pas d'accélération tangentielle en raison de la nature uniforme du mouvement. Ainsi, la vitesse du satellite au carré peut être exprimée comme GMt divisé par RT plus Z.
Ensuite, Théobald aborde la question de la révolution du satellite. Il explique que la période de révolution correspond au temps qu'il faut au satellite pour faire le tour de la Terre. Il utilise la formule de la distance parcourue divisée par la vitesse constante du satellite pour trouver la période de révolution. En substituant la valeur de la vitesse du satellite dans la formule, il obtient une période de révolution de 5653 secondes, soit environ 1h34. Il conclut que le satellite fait environ 15,3 fois le tour de la Terre en une journée, ce qui est cohérent avec les informations fournies.
Ensuite, Théobald aborde une situation particulière où deux satellites sont impliqués. Il explique que le premier satellite survole une zone où le champ gravitationnel n'est pas centripète, tandis que le deuxième satellite survole une zone où le champ gravitationnel est centripète. La question posée est de savoir si la distance entre les deux satellites restera constante.
Théobald commence par étudier le deuxième satellite, qui suit un mouvement circulaire uniforme. Son accélération est seulement portée par le vecteur normal, et sa vitesse est constante. En revanche, le premier satellite subit un champ gravitationnel qui comporte à la fois une composante normale et une composante tangentielle. Sa vitesse n'est pas constante et il subit un mouvement circulaire accéléré. Théobald explique que dans ce cas, la distance entre les deux satellites augmentera, car le premier satellite accélère tandis que le deuxième satellite maintient une vitesse constante.
Théobald conclut en encourageant les spectateurs à poser des questions et annonce une prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La mission Grace-Fo (3)
Dans cette vidéo, Théobald de Studio explique le principe de l'interféromètre embarqué utilisé dans la mission GRASFO, qui consiste à mesurer la distance entre deux satellites jumeaux situés sur la même orbite pour étudier les changements du champ gravitationnel terrestre. Pour cela, un laser est envoyé sur un miroir semi-réfléchissant, séparant ainsi le laser en deux parties. L'interféromètre permet de détecter les interférences entre ces deux sources cohérentes pour mesurer la distance entre les satellites. La différence de marche entre les chemins optiques est calculée en fonction de la longueur d'onde et de la distance entre les miroirs. En montrant que la variation de distance entre les satellites correspond à deux états successifs d'interférence constructive, il est démontré que la plus petite variation de distance détectable par l'interféromètre est de 532 nanomètres, ce qui est très précis.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La mission Grace-Fo (4)
Dans cette vidéo, Théobald de Studio nous explique le fonctionnement d'un accéléromètre utilisé dans le cadre de la mission Grasse-Faux. L'accéléromètre permet d'accéder au champ gravitationnel terrestre en mesurant les forces non gravitationnelles.
L'accéléromètre est composé d'une masse d'épreuve située au centre d'une cage électrostatique. Cette masse subit un déplacement lorsque soumise à une force non gravitationnelle, ce qui modifie la capacité des trois paires de condensateurs. Dans cette étude, on se concentre sur un condensateur plan avec une armature mobile à gauche et une armature fixe. Une tension U est appliquée entre les deux armatures.
L'influence du déplacement X, choisi comme positif, sur la capacité C du condensateur est discutée. La capacité C est inversément proportionnelle à X, donc si X augmente, C diminue.
L'expression du champ électrique E entre les plaques du condensateur est déterminée en fonction de U, E, X et du vecteur unitaire i. On rappelle que le champ électrique entre deux plaques parallèles a pour norme U/D et est dirigé de la plaque positive vers la plaque négative. Ainsi, E est égal à U/(E+X) et est porté par le vecteur unitaire i.
L'armature mobile est soumise au champ E1 créé par l'armature fixe. Selon les lois de l'électrostatique, E1 est égal à E/2. La force mécanique subie par l'armature mobile, modélisée par F, est opposée à E. Parmi les quatre schémas proposés, le deuxième représente correctement le champ électrique E et la force électrique F car E va du plus vers le moins et F est opposée à E.
Dans la dernière question, on explique que le condensateur est associé à un deuxième condensateur et que la masse d'épreuve est mobile entre les deux armatures fixes. Les forces électrostatiques exercées par les deux armatures fixes se compensent, donc leur somme est nulle. Cela entraîne que les champs électriques EG à gauche et ED à droite sont égaux. Ainsi, la relation entre les champs électriques EG et ED est que EG = ED.
Ce cours explique donc le fonctionnement d'un accéléromètre dans le contexte de la mission Grasse-Faux et comprend des explications sur la capacité du condensateur, le champ électrique et les forces électriques.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Protection des fondations en acier des éoliennes en mer (1)
Dans cette vidéo, Théobald du Studio explique la protection des éoliennes en mer contre la corrosion. Deux méthodes principales sont utilisées : l'anode sacrificielle et la protection par courant imposé. Dans cet exercice, il se concentre sur la protection cathodique avec une anode sacrificielle en aluminium. Il cherche à vérifier si le fer peut être protégé de l'oxydation en le mettant en contact avec de l'aluminium. La réaction qui modélise cette transformation est 2Al + 3Fe2+ -> 3Al2+ + 3Fe. Le quotient de réaction initial est exprimé en fonction des concentrations en ions Al3+ et Fe2+, et sa valeur est calculée. Grâce à la comparaison de ce quotient avec la constante d'équilibre, on détermine que la réaction se fait dans le sens direct. La réaction à l'électrode d'aluminium est décrite comme l'oxydation de l'aluminium solide en ions Al3+. L'intensité électrique négative indiquée sur le schéma est cohérente avec cette réponse. Enfin, l'électrode d'aluminium est identifiée comme l'anode dans la pile. Dans la prochaine vidéo, Théobald continuera à expliquer comment protéger les éoliennes et déterminer la quantité d'aluminium nécessaire.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Protection des fondations en acier des éoliennes en mer (2)
Dans cette vidéo, Oval2Studio aborde l'exercice sur la protection cathodique des éoliennes en aluminium. L'objectif est de déterminer la masse d'aluminium nécessaire pour protéger complètement les éoliennes. On sait que l'aluminium réagit préférentiellement avec le dioxygène dissous dans l'eau, ce qui en fait le matériau de choix pour la protection cathodique.
Pour trouver la masse d'aluminium nécessaire, on commence par écrire l'équation de réaction de corrosion de l'aluminium par le dioxygène dissous. En équilibrant les deux demi-équations correspondantes aux couples redox présents, on obtient l'équation de réaction complète.
Ensuite, on nous dit qu'une protection efficace correspond à un courant électrique d'intensité de 400 A. On nous demande donc de calculer la masse d'aluminium nécessaire pour une durée de 25 ans. Pour cela, on utilise la relation entre l'intensité du courant électrique et la capacité électrique, qui est égale au nombre d'électrons échangés multiplié par la constante de Faraday. On utilise également la demi-équation du couple AL-AL3+ pour trouver la quantité de matière d'aluminium.
En combinant toutes ces informations, on obtient que la masse d'aluminium nécessaire est de 2,9 x 10^4 kilogrammes. Cependant, cette quantité est très importante et coûteuse pour le constructeur, en plus des rejets d'ions aluminium 3 dans la mer. C'est pourquoi le constructeur a choisi une autre solution que la protection cathodique par un matériau sacrificiel.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Additif alimentaire pour les agneaux (1)
Dans cette vidéo, Théobald de Cidéaux explique le principe du titrage par suivi conductimétrique. Il aborde l'exemple du titrage des additifs alimentaires dans les agneaux pour éviter certaines maladies. L'éleveur administre une solution de chlorure d'ammonium à un agneau de 24 kg, et le but de l'exercice est de vérifier si sa préparation est conforme aux recommandations du site des partenaires de la production animale en France.
Le titrage conductimétrique consiste à titrer un volume donné de la solution préparée par l'éleveur avec une solution titrante d'hydroxyde de sodium, et à mesurer la conductivité de la solution pendant le processus.
La première question de l'exercice demande de déterminer si la réaction chimique entre le chlorure d'ammonium et l'hydroxyde de sodium est une réaction acido-basique ou une réaction d'oxydo-réduction. En analysant les ions NH4+ et HO-, on constate qu'il y a un transfert de protons (H+), ce qui indique qu'il s'agit d'une réaction acido-basique.
Ensuite, il est demandé de réaliser un schéma légendaire du dispositif de titrage conductimétrique. Le schéma proposé comprend une bécher, une burette graduée, une sonde reliée au conductimètre, et une potence avec un agitateur magnétique.
On nous montre ensuite une courbe obtenue à la fin du titrage, et on nous demande d'exprimer la concentration en quantité de matière de chlorure d'ammonium de la solution préparée par l'éleveur, puis de calculer sa valeur. En analysant l'équation de la réaction de titrage, on détermine que les réactifs ont été introduits en proportion stoichiométrique, ce qui permet d'établir une relation entre les quantités de matière des deux espèces chimiques. En utilisant cette relation, on détermine la concentration de la solution préparée par l'éleveur grâce aux données du titrage.
Ensuite, on nous demande de proposer un encadrement de la concentration de la solution préparée par l'éleveur en prenant en compte les incertitudes. On utilise les incertitudes absolues des différentes verreries utilisées dans le titrage pour déterminer l'incertitude absolue sur la concentration.
Enfin, on nous demande de calculer la masse de chlorure d'ammonium apportée quotidiennement par l'éleveur à l'agneau, et de comparer ce résultat à la valeur préconisée par le site des partenaires de la production animale en France. On utilise la concentration de la solution préparée par l'éleveur et la quantité de solution donnée à l'agneau pour calculer la masse de chlorure d'ammonium. On compare ensuite cette valeur à celle préconisée par le site, en prenant en compte une marge d'erreur de 10%.
L'éleveur a donc bien respecté les recommandations du site, car la masse de chlorure d'ammonium donnée à l'agneau se situe dans l'intervalle préconisé.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Additif alimentaire pour les agneaux (2)
Bonjour à tous! Dans cette vidéo, nous nous intéressons au code Python nécessaire pour simuler un titrage par conductimétrie. Nous avons utilisé l'exemple d'un éleveur donnant des compléments alimentaires à son agneau et nous avons effectué un titrage pour évaluer la concentration de la solution donnée à l'animal. Nous avons donc titré les ions NH4+ grâce aux ions HO-.
Dans la première partie, nous avons complété le code aux lignes 6, 7 et 8. Les variables A, B et C correspondent aux nombres stoichiométriques des espèces chimiques dans l'équation de réaction. Dans notre cas, A=1, B=1 et C=1 car les nombres stoichiométriques de tous les réactifs et produits dans notre équation sont égaux à 1.
Ensuite, nous avons identifié les deux espèces chimiques correspondant aux variables NSA et NSB. NSA représente la quantité de matière en ions Cl- (chlorure) et NSB représente la quantité de matière en ions Na+ (sodium).
Ensuite, nous avons analysé les 5 graphiques obtenus à l'aide du programme Python. Nous avons utilisé un tableau de présence des différentes espèces chimiques en solution pour déterminer quelles espèces étaient représentées sur chaque graphique. Avant l'équivalence, les ions HO- sont ajoutés et réagissent immédiatement avec les ions NH4+, conduisant à une diminution de la quantité de matière en NH4+ et à la formation de NH3. Après l'équivalence, les ions HO- et Na+ sont ajoutés mais les ions NH4+ ne sont plus présents en solution.
Enfin, nous avons complété le code aux lignes 12 (calcul du volume à l'équivalence) et 19 (calcul de Nb). Le volume à l'équivalence correspond à la quantité de matière en ions HO- apportée à l'équivalence, ce qui peut être calculé en utilisant les concentrations et volumes initiaux des réactifs. Nb représente la quantité de matière en ions HO- en solution, qui est nulle avant l'équivalence car les ions HO- sont ajoutés et consommés immédiatement en réagissant avec les ions NH4+.
J'espère que ce résumé en SEO friendly du cours vous a été utile. Si vous avez des questions, n'hésitez pas à les poser en commentaire!
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

test greg
Dans cette vidéo, nous étudions la caractérisation de l'orbite d'un satellite dans le cadre de la mission GRAFO. Deux satellites jumeaux sont envoyés sur la même orbite. L'attraction gravitationnelle de la planète varie légèrement d'un mois à l'autre en raison d'une fraction infime de sa masse qui est en mouvement constant. Cette variation peut rendre l'attraction gravitationnelle tantôt centripète tantôt non centripète.
Dans la première partie, nous nous intéressons à la caractérisation de l'orbite. Les satellites de cette mission ont une orbite quasi-circulaire avec une altitude de 490 km par rapport à la Terre. L'inclinaison du plan de la trajectoire par rapport à l'équateur est de 89 degrés. Les deux satellites sont situés à une distance L l'un de l'autre.
Nous examinons les forces qui s'appliquent sur ces satellites, en nous concentrant sur le mouvement d'un satellite pour le moment. Nous devons d'abord dessiner un schéma représentant la Terre, le rayon RT, le satellite et le vecteur n qui est le vecteur unitaire du satellite vers la Terre.
Ensuite, nous devons donner l'expression vectorielle de la force gravitationnelle F exercée par la Terre sur le satellite. En notant cette force sur le schéma, nous pouvons exprimer cette force gravitationnelle en utilisant la formule G fois la masse de la Terre fois la masse du satellite divisé par la distance Terre-satellite au carré, portée par le vecteur n.
Nous déduisons ensuite l'expression du champ vectoriel terrestre G à partir de l'expression de la force gravitationnelle. Le champ gravitationnel est donc G fois la masse de la Terre fois la masse du satellite divisé par RT plus z au carré, porté par le vecteur n.
En considérant uniquement l'action de la Terre, nous établissons l'expression vectorielle de l'accélération a du satellite en utilisant le principe fondamental de la dynamique. L'accélération est donc gmt sur rt plus z au carré, portée par le vecteur n.
Ensuite, nous démontrons que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Pour cela, nous supposons que l'orbite est circulaire et montrons que lorsque le mouvement est circulaire, l'accélération tangentielle est nulle, ce qui signifie que la vitesse du satellite est constante et donc que le mouvement est uniforme.
En concluant cette partie de l'exercice, nous expliquons que si vous avez des questions, n'hésitez pas à les poser en commentaire et que nous y répondrons avec plaisir.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

test greg
Dans cette vidéo, Théobald de Studio aborde la caractérisation de l'orbite d'un satellite dans le cadre de la mission GRAFO, qui envoie deux satellites jumeaux sur la même orbite. Il mentionne que l'attraction gravitationnelle de la planète varie faiblement en raison du mouvement continu d'une fraction de la masse terrestre, ce qui peut rendre cette attraction gravitationnelle tantôt centripète et tantôt non.
Dans la première partie de la vidéo, Théobald se concentre sur la caractérisation de l'orbite des satellites. Il explique que l'orbite est quasi-circulaire, avec une altitude z de 490 km, et une inclinaison du plan de trajectoire à l'équateur de 89°. Il nous informe également que les deux satellites sont situés à une distance L l'un de l'autre, et examine les forces appliquées sur ces satellites. Il ne se penche que sur le mouvement d'un satellite pour le moment. Il nous demande de représenter la Terre, son rayon RT, et le satellite avec son centre de masse S, ainsi que le vecteur unitaire n allant du satellite vers la Terre.
Ensuite, il nous demande de donner l'expression vectorielle de la force gravitationnelle F de T sur S exercée par la Terre sur le satellite. Théobald suggère de refaire le schéma et de noter la force F de T sur S, qui est dirigée du satellite vers la Terre. Il explique que cette force gravitationnelle peut être exprimée comme G masse de la Terre fois masse du satellite divisé par la distance Terre-satellite au carré, portée par le vecteur n. Il souligne que cette force est attractive et doit attirer le satellite et la Terre, donc elle est dirigée vers la Terre.
Ensuite, il nous demande de déduire l'expression du champ vectoriel terrestre G. En utilisant la relation entre la force gravitationnelle et le champ gravitationnel, Théobald calcule l'expression du champ gravitationnel, qui est G masse de la Terre fois masse du satellite divisé par RT plus z au carré, porté par le vecteur n.
Il poursuit en établissant l'expression vectorielle de l'accélération a du satellite en considérant uniquement l'action de la Terre. En utilisant le principe fondamental de la dynamique, Théobald montre que la somme des forces extérieures est égale à la masse du satellite multipliée par son accélération. En utilisant l'expression de la force gravitationnelle calculée précédemment, il trouve l'expression de l'accélération, qui est g fois masse du satellite divisé par RT plus z au carré, toujours portée par le vecteur n. Il note que l'accélération est égale au champ gravitationnel g dans ce cas.
Ensuite, il montre que dans le cadre de l'approximation d'une orbite circulaire, le mouvement du satellite est uniforme. Il explique que pour un mouvement circulaire, l'accélération peut être décomposée en une accélération tangentielle et une accélération normale. En utilisant cette décomposition et l'expression de l'accélération, il montre que si le mouvement est circulaire, la vitesse du satellite est constante.
Pour conclure cette première partie de la vidéo, Théobald invite les spectateurs à poser leurs questions dans les commentaires et promet de répondre avec plaisir.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Analyse d’un pigment à base d’oxyde de fer (1)
Dans cette vidéo, nous nous intéressons à l'analyse d'un pigment à base d'oxyde de fer. Un pigment est une espèce chimique colorante et insoluble dans le milieu qu'elle colore. Nous allons analyser une poudre colorante contenant un pigment d'oxyde de fer de formule Fe2O3. Le fabricant indique que la teneur en oxyde de fer de cette poudre est de 5%. Nous allons effectuer une analyse quantitative de ce produit en utilisant une méthode de dosage par étalonnage.
Dans une première étape, nous préparons une gamme d'étalons contenant des ions fer 3. Pour cela, nous préparons une solution mère S0 contenant des ions fer 3 en utilisant du chlorure de fer 3 hexahydraté (FeCl3-6H2O). Nous devons écrire l'équation de dissolution de ce composé et déterminer la masse de solide nécessaire pour obtenir la solution S0.
L'équation de dissolution du chlorure de fer 3 hexahydraté est FeCl3-6H2O -> Fe3+ + 3Cl- + 6H2O. La masse de solide nécessaire pour obtenir la solution S0 est calculée en utilisant la quantité de matière en ion fer 3, qui est égale à la quantité de matière en chlorure de fer 3 hexahydraté. Nous obtenons une masse de 3,0 x 10-2 g.
Ensuite, nous préparons différentes solutions de la gamme d'étalonnage en diluant la solution mère S0. Nous devons estimer le volume à prélever de la solution mère pour préparer la solution S5. Nous utilisons la conservation de la quantité de matière et de la masse pour trouver que le volume à prélever est de 10,0 mL. Nous utiliserons une pipette jaugée de 10,0 mL pour cette étape.
Ensuite, nous réalisons un spectre d'absorption d'une solution du ion fer 3 en présence du ion thiocyanate, dans les mêmes conditions que les solutions de la gamme étalon. Nous devons déterminer la couleur de la solution en utilisant la méthode du maximum d'absorption. Nous trouvons que la solution est de couleur rouge.
Enfin, nous devons indiquer la longueur d'onde la plus adaptée pour effectuer les mesures d'absorbance. La longueur d'onde la plus adaptée correspond au maximum d'absorption, qui est d'environ 490 nm dans ce cas.
N'hésitez pas à poser vos questions en commentaire et nous nous retrouverons pour la suite de l'exercice.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

Analyse d’un pigment à base d’oxyde de fer (2)
Dans cette vidéo, Théobald de Cidéo aborde le sujet de l'analyse d'un pigment à base d'oxyde de fer. Le pigment est insoluble dans le milieu qu'il colore et le fabricant prétend que la teneur en oxyde de fer de la poudre est de 5%. Pour vérifier cela, un dosage par étalonnage est effectué.
La première partie de l'exercice consiste à préparer une gamme étalon contenant des ions de fer. Ensuite, une courbe d'étalonnage est réalisée en mesurant l'absorbance des solutions S1 à S5 avec un spectrophotomètre réglé à la longueur d'onde lambda0. La représentation graphique de cette courbe est compatible avec la loi de Berlembert, qui établit une relation entre l'absorbance et la concentration. La droite obtenue passe par l'origine, ce qui montre que l'absorbance est proportionnelle à la concentration molaire.
Pour établir la relation exprimant l'absorbance en fonction de la concentration en masse d'ion fer 3, on trace une droite qui passe au-dessus et en dessous des points de mesure. En choisissant deux points arbitraires sur cette droite, on peut calculer la constante K qui est égale à la différence d'ordonnées divisée par la différence d'abscisses.
La troisième partie de l'exercice concerne la préparation de l'échantillon. Pour augmenter la solubilité du pigment, 100mg de produit sont dissous dans 20mg d'acide chlorhydrique concentré. Ensuite, le mélange est introduit dans une fiole de 100mg et complété avec de l'eau déminéralisée. Par dilution au dixième, la solution S est préparée et ensuite l'absorbance de l'échantillon est mesurée à la longueur d'onde lambda0.
Il est généralement nécessaire de diluer la solution S dans ce type de dosage car la loi de Berlembert s'applique pour des solutions diluées. En utilisant la valeur de l'absorbance mesurée, on peut déterminer la teneur de la poudre en oxyde de fer. Cette teneur est donnée par la masse d'oxyde de fer dans la poudre divisée par la masse de la poudre. En effectuant les calculs nécessaires, on obtient une teneur de 5,1%, ce qui est conforme à l'indication du fabricant.
Il s'agit d'un exercice complexe mais formateur pour comprendre les dosages par étalonnage. Théobald encourage les spectateurs à travailler dessus et à poser des questions dans les commentaires si besoin.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La vitamine C sans sucre (1)
Dans cette vidéo, Théobald de Cidéo nous présente un exercice de chimie sur l'aspartame. Il explique que l'aspartame est une molécule présente dans la vitamine C et qu'il souhaite trouver son spectre infrarouge. Il explique également que la vitamine C, également appelée acide ascorbique, joue un rôle essentiel dans le métabolisme. Il précise que l'aspartame est un édulcorant de synthèse choisi pour son pouvoir sucrant élevé et sa faible teneur en calories.
Le cours poursuit en mentionnant les différentes caractéristiques de l'aspartame, notamment les trois groupes fonctionnels présents dans sa formule topologique. Ces groupes sont identifiés comme étant un acide carboxylique, un amine et un ester.
Ensuite, Théobald explique que l'aspartame peut être synthétisé en laboratoire à partir de l'acide aspartique, dont la formule semi-développée est donnée. Il explique brièvement comment représenter cette formule.
Ensuite, le cours aborde les spectres obtenus par spectroscopie infrarouge de l'aspartame et de l'acide aspartique. Théobald explique que l'objectif est d'identifier le spectre de l'aspartame. Il décrit les bandes caractéristiques qui devraient être présentes dans le spectre infrarouge de l'aspartame en fonction des différents groupes fonctionnels.
En analysant les deux spectres, Théobald conclut que le spectre 2 correspond au spectre de l'aspartame, car il présente toutes les bandes caractéristiques attendues.
La vidéo se termine en encourageant les spectateurs à poser des questions dans les commentaires et en annonçant une prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La vitamine C sans sucre (2)
Dans cette vidéo, Théobald de Studio aborde la synthèse de l'aspartame à partir de la vitamine C, plus précisément de l'acide ascorbique. On nous explique que cette synthèse se déroule en plusieurs étapes, et que dans cette transcription, on se concentre sur la première étape qui consiste à transformer l'espèce chimique A en l'espèce chimique C.
Différents protocoles sont présentés, avec des masses et des rendements variables. Dans la première question, on nous demande de déterminer le volume de réactif B liquide à prélever dans le protocole 1. Pour cela, on utilise la formule masse divisée par masse volumique et on obtient un volume de 1,0 millilitres.
La deuxième question porte sur le rendement de la synthèse avec le protocole 1. Le rendement se calcule en divisant la masse de produit C obtenue expérimentalement par la masse de produit C obtenue théoriquement. On nous donne la masse expérimentale de 4,12 grammes et on calcule la masse théorique de 4,30 grammes. Le rendement est donc de 96%.
Ensuite, on nous demande pourquoi le rendement du protocole 1 est supérieur à celui du protocole 2, et de proposer un autre protocole pour améliorer le rendement. La différence entre les deux protocoles réside dans la quantité de matière de réactif A utilisée. Dans le protocole 1, on en utilise plus, ce qui permet à A d'être en excès et d'augmenter le rendement. Pour améliorer le rendement, on propose d'éliminer un des produits, comme l'eau, pour favoriser la production des produits.
Enfin, en analysant un tableau présenté, on identifie le rôle du palladium sur carbone. On remarque que sa présence accélère la durée de la réaction, ce qui indique que le palladium sur carbone est un catalyseur.
La partie C de cet exercice sera traitée dans une prochaine vidéo.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La vitamine C sans sucre (3)
Dans cette vidéo, Théobald de Cidéo aborde le sujet de l'acide ascorbique, qui est le nom scientifique de la vitamine C. Il explique comment dissoudre cet acide dans l'eau et présente un exercice qui concerne le BAC de 2022 en Amérique du Nord. L'exercice consiste à calculer la concentration en quantité de matière de l'acide ascorbique lorsqu'un comprimé de 0,50 g est dissout dans 200,0 ml d'eau. Pour cela, Théobald utilise la formule de concentration en quantité de matière qui est le nombre de moles divisé par le volume de la solution. Il montre ensuite comment calculer cette concentration en utilisant la masse d'acide ascorbique, la masse molaire de l'acide ascorbique et le volume de la solution. Il obtient une concentration de 1,4 fois 10 moins 2 moles par litre, ce qui correspond à la réponse B de l'exercice. Ensuite, Théobald explique que l'acide ascorbique est un acide faible et que sa réaction avec l'eau est une réaction acido-basique. Il présente les couples d'espèces en présence et montre que la réaction se fait entre l'acide ascorbique et l'eau pour former les ions ascorbate et H3O+. Il mentionne également que le pH à l'équilibre de la solution est de 2,9. Théobald montre ensuite comment montrer que la constante d'acidité Ka peut s'écrire sous la forme donnée dans l'énoncé de l'exercice en utilisant les concentrations en ions H3O+ et ascorbate à l'équilibre et la concentration en quantité de matière apportée d'acide ascorbique. Il utilise un tableau d'avancement pour caractériser l'équilibre et montre que les concentrations en ions H3O+ et ascorbate à l'équilibre sont égales. En utilisant ces valeurs, il détermine la constante d'équilibre Ka. Il utilise ensuite Ka pour calculer le pKa du couple acide-ascorbique-ion-ascorbate, qui est de 3,9. Enfin, Théobald demande de représenter le diagramme de prédominance du couple ascorbique-ion-ascorbate en fonction du pH et de déduire la forme majoritaire dans l'estomac, où le pH est d'environ 2. Il explique que l'acide prédomine à pH faible et la base à pH élevé, et montre que dans l'estomac, qui a un pH de 2, la forme majoritaire est l'acide ascorbique. Théobald conclut en encourageant les spectateurs à poser des questions en commentaire et leur souhaite bonne chance pour leurs révisions.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La vitamine C sans sucre (4)
Dans cette vidéo, Théoval de Cedéo poursuit l'exercice sur la vitamine C en essayant de déterminer la masse d'acide ascorbique dans un comprimé de vitamine C. Le fabricant donne des informations sur la larose corbine, un comprimé contenant 500mg de vitamine C sous forme d'acide ascorbique et d'ascorbate de sodium. L'objectif est de vérifier si la masse d'acide ascorbique dans un comprimé est bien de 200mg.
Pour cela, Théoval dissout un comprimé dans de l'eau distillée pour obtenir une solution S de volume V0 égal à 250mL. Un volume de 40mL de cette solution est prélevé et titré avec une solution d'hydroxyde de sodium pour déterminer la masse en acide ascorbique.
La réaction de titrage est la suivante : acide ascorbique + hydroxyde de sodium → ascorbate + eau. La conductivité de la solution est mesurée tout au long du titrage.
Les courbes de conductivité en fonction du volume d'hydroxyde de sodium versé montrent une augmentation de la conductivité avec l'augmentation du volume versé. Avant l'équivalence, les concentrations des ions HO-, Na+ et ascorbate augmentent. Après l'équivalence, la concentration en ions ascorbate ne change plus. Cette évolution de la conductivité est cohérente avec les observations expérimentales.
En utilisant les courbes, il est possible de déterminer la concentration en acide ascorbique de la solution titrée, qui est de 4,3 x 10-3 mol/L. En utilisant cette concentration, le volume de la solution S0 et la masse molaire de l'acide ascorbique, la masse d'acide ascorbique contenue dans un comprimé est calculée et trouvée être de 0,19 g.
En comparant cette valeur à la valeur annoncée par le fabricant (200 mg), on trouve un rapport de 1, ce qui indique que la mesure est compatible avec la valeur de référence. Ainsi, la valeur mesurée est cohérente avec celle indiquée par le fabricant.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La pente d'eau de Montech (1)
Aujourd'hui, nous étudions la pente d'eau de Montaigue, un ascenseur à bateau devenu un site touristique depuis 2021. L'ascenseur permettait de monter ou descendre les bateaux en 20 minutes. Dans cette première partie, nous étudions le mouvement du système, dont le centre de masse est G. Le système se déplace selon l'axe OX avec un angle alpha par rapport à l'horizontale. Nous montrons que l'accélération du système est constante entre t = 0 et t1 = 100 secondes, et qu'elle vaut A0 = 1,20 x 10^-2 m/s^2. En intégrant l'accélération, nous obtenons l'équation horaire de la vitesse, V(t) = A0t. En intégrant la vitesse, nous obtenons l'équation horaire de la position, x(t) = 1,5A0t^2. En analysant les chronophotographies, nous déterminons que la chronophotographie C représente le mouvement du système entre t0 et t1, car les intervalles de temps et de distance sont réguliers.
Corrigés de BAC
Bac Physique-Chimie
MPSI/PCSI

La pente d'eau de Montech (2)
Dans cette vidéo, Théobald continue l'exercice sur l'ascenseur à bateau. Dans la première partie, il étudie dynamiquement le système et dans la deuxième partie, il essaie de se placer loin du bateau pour l'observer à l'aide d'une lunette.
Le système est composé du bateau, de l'eau et du masque. Le centre de masse du bateau se déplace le long de la pente d'OX et est soumis à quatre forces : poids, réaction normale de la pente, forces automotrices et force de frottement du masque et de l'eau le long de la pente.
On nous demande de déterminer le schéma qui représente le mieux la situation entre deux moments donnés et de justifier notre réponse en associant chaque vecteur force aux forces décrites précédemment.
En étudiant la situation entre t0 et t1, on trouve que l'accélération est positive selon l'axe plus ux. Donc la somme des forces extérieures doit également être selon plus ux. En compar


