Online Learning Courses

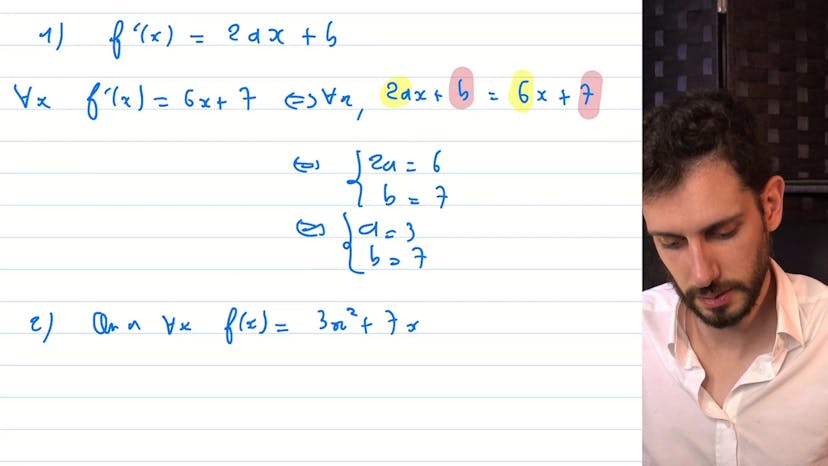
Trouver la formule d'une fonction

Ce cours traite de la résolution d'une fonction inconnue à partir de sources d'informations données. On commence par déterminer une expression possible de la fonction f2x en trouvant les valeurs des réels a et b. Pour cela, on dérive f2x et on l'égalise à 6x + 7. On en déduit que a = 3 et b = 7. Pour trouver la valeur de c, qui est la troisième inconnue, on utilise une information supplémentaire qui est que la courbe de f passe par le point (1,6). En mettant x = 1 dans f2x, on obtient une équation reliant c à 3 et 7, d'où on en déduit que c = -4. En combinant toutes les informations, on trouve que f2x = 3x2 + 7x - 4. La méthode consiste donc à trouver autant de sources d'information que d'inconnues pour résoudre la fonction.

Approximation affine

Dans ce cours sur l'approximation affine, nous examinons le concept de dérivation et expliquons comment on peut approximer une courbe en utilisant sa tangente. Tout d'abord, nous montrons que pour une fonction dérivable f, du point a à a plus h, le taux de variation est approximativement égal à f'(a). Cette formule peut être exprimée comme f(a + h) ≈ f(a) + h * f'(a). Pour mieux comprendre cette approximation, nous utilisons des graphiques. Par exemple, nous observons que lorsque nous zoomons sur une courbe, la tangente et la courbe se confondent dans une certaine plage. Nous illustrons cette idée avec différents exemples, tels que la fonction 1 + x². Ensuite, nous montrons comment cette approximation peut être utilisée pour justifier une équation particulière. Par exemple, pour la fonction f(x) = x², nous démontrons que lorsque h est proche de 0, on peut écrire 1 + h² ≈ 1 + 2h. Cette équation peut être dérivée de la formule précédente en utilisant f(1) = 1 et f'(x) = 2x. Enfin, nous utilisons cette approximation pour obtenir des valeurs approchées sans utiliser de calculatrice. Par exemple, nous approchons 1,05 et 0,999 en utilisant l'équation 1 + 2h avec h = 0,05 et h = -0,001 respectivement. Nous comparons ensuite ces valeurs approchées avec les valeurs exactes en utilisant une calculatrice. En résumé, l'approximation affine est une méthode qui permet d'approximer une courbe par sa tangente lorsque l'on se rapproche suffisamment de la courbe. Cela peut être utile pour calculer des valeurs approximatives sans avoir besoin d'une calculatrice.

Classique - Fonction à paramètre

Le cours porte sur les courbes avec un paramètre et les exercices de dérivation. Des fonctions sont présentées en fonction du paramètre m, qui peut varier. Dans le premier exercice, l'objectif est de trouver deux points d'abscisse pour lesquels les tangentes sont parallèles à l'axe des abscisses. En calculant la dérivée de la fonction g, on peut trouver ces deux points. Dans le deuxième exercice, le but est de déterminer pour quelle valeur de m il y a une seule solution pour la tangente parallèle à l'axe des abscisses. En calculant le delta de la fonction g, on peut trouver cette valeur. La réponse est m=4/3 et la solution unique pour la tangente parallèle à x-axis est x=1.5.

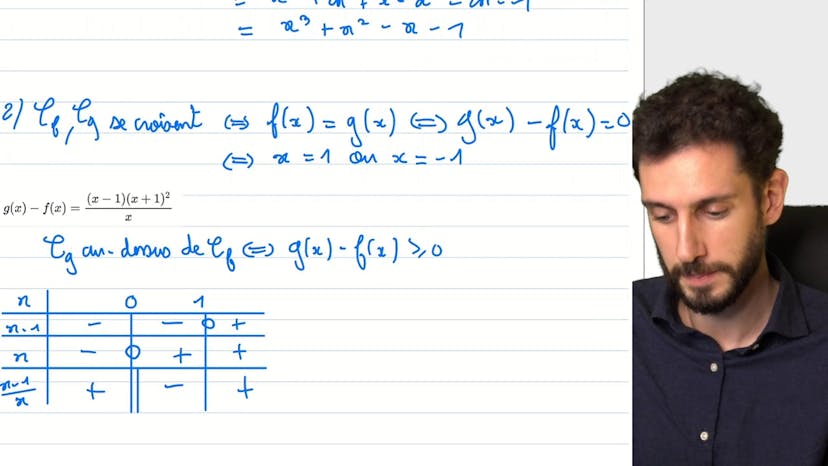
Des courbes tangentes

Ce cours présente un exercice qui introduit la notion de tangence entre deux courbes. Les deux courbes données sont une fonction f, qui est une hyperbole décrite par l'équation 5x + 4 / 4x, et une fonction g, qui est une parabole décrite par l'équation x^2 + x + 1/4. D'abord, on sépare la fraction de f en deux parties, simplifiant ainsi 5x / 4x à 5/4 et 4 / 4x à 1 / x. Cela rend l'expression de f beaucoup plus simple. Ensuite, on observe que l'expression de g peut être factorisée sous la forme (x + 1)^2. Cette observation n'est pas nécessaire mais peut être utile pour développer une intuition rapide. On montre graphiquement que les deux courbes se touchent en un point unique, situé à l'abscisse (-1, 0.25). Ensuite, on effectue des calculs pour montrer que g(2x) - f(2x) = x^3 + x^2 - x - 1. On utilise deux méthodes: la factorisation en utilisant les identités remarquables, et l'utilisation de la réponse donnée à l'exercice pour développer l'expression. En utilisant ces calculs, on déduit que les points d'intersection des courbes sont x = 1 et x = -1. On détermine également la position relative des courbes cf et cg en utilisant un tableau de signe. On conclut que cg est au-dessus de cf lorsque x < 0 et lorsque x < 1. Enfin, on montre que les courbes admettent la même tangente au point (-1, 0.25), en calculant les dérivées f'(-1) = -1 et g'(-1) = -1. En conclusion, cet exercice présente une situation intéressante où deux courbes se touchent en un point unique et admettent la même tangente à ce point.

Fonction définie par morceaux

La vidéo explique comment représenter une fonction définie par morceaux et comment déterminer si elle est dérivable en un point spécifique. On utilise l'exemple d'une fonction constituée d'une parabole jusqu'à 1 et une fonction affine de 1 jusqu'à l'infini. Cette fonction est représentée graphiquement et il est démontré qu'elle est dérivable dans les deux parties de la fonction, mais pas en 1. Le calcul des taux d'accroissement de chaque côté de 1 montre que les limites ne sont pas égales, ce qui signifie que la fonction n'est pas dérivable.

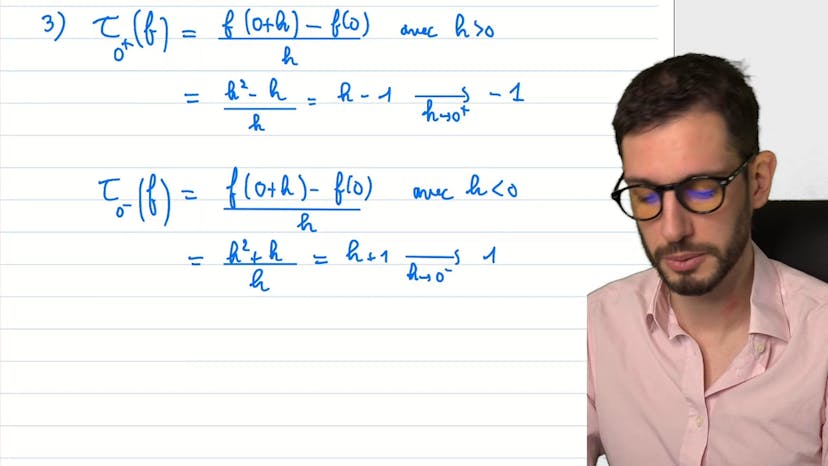
Une famille de fonctions !

Dans cette vidéo, il s'agit d'une transcription d'un cours sur une fonction avec une valeur absolue. Le professeur aborde plusieurs étapes pour étudier cette fonction. Tout d'abord, il explique que la valeur absolue pose des difficultés, notamment en ce qui concerne la tracé de la fonction et sa non-dérivabilité en zéro. Il propose donc de commencer par vérifier si la fonction est paire ou impaire, car cela peut permettre de réduire l'étude de la fonction à l'ensemble des réels positifs en utilisant une symétrie par rapport à l'axe Y. Dans cet exemple, la fonction est paire. Ensuite, le professeur propose d'écrire la fonction en utilisant différentes expressions sur différents intervalles pour se débarrasser de la valeur absolue. Il donne l'expression de la fonction pour les réels positifs (f(x) = x² - x) et pour les réels négatifs (f(x) = -x). Il explique également qu'il va tracer la fonction uniquement sur les réels positifs, mais qu'il a besoin de connaître l'expression sur les réels négatifs pour cela. Ensuite, le professeur aborde l'étude de la dérivabilité de la fonction. Il calcule le taux d'accroissement de la fonction en zéro en utilisant deux expressions différentes, une pour les réels positifs et une pour les réels négatifs. Il obtient deux limites différentes pour le taux d'accroissement en approchant zéro par la droite et par la gauche. Il conclut donc que la fonction n'est pas dérivable en zéro. Enfin, le professeur propose de continuer l'étude de la fonction sur l'ensemble des réels positifs. Il indique que la fonction est un polynôme du deuxième degré qui s'annule en zéro et en un. Il précise également que le maximum de la fonction se trouve en un demi. Il trace ensuite le graphe de la fonction sur les réels positifs, qui est une parabole. Il explique ensuite comment obtenir le graphe de la fonction sur les réels négatifs en utilisant une symétrie par rapport à l'axe des ordonnées. Il constate également la présence d'un point de non dérivabilité où la tangente a une pente de -1 d'un côté et une pente de 1 de l'autre côté. Il termine en notant que même si la fonction présente des points avec des "coins", on peut tout de même l'étudier et la tracer sans trop de difficultés. En conclusion, ce cours a abordé différentes étapes pour étudier une fonction avec une valeur absolue, notamment en vérifiant sa parité, en écrivant l'expression de la fonction sur différents intervalles, en étudiant sa dérivabilité et en traçant le graphe de la fonction.

Convexité étude COMPLETE

Aucun résumé n'est disponible pour cette vidéo

Fonctions cubes et convexité

Le cours aborde différents paramètres (A, B, C, D) et propose une démonstration générale sur les fonctions x³. Il met en évidence l'intuition graphique selon laquelle une fonction x³ avec un coefficient positif est concave, tandis qu'une fonction avec un coefficient négatif est convexe. Pour étudier la convexité de la fonction f, il faut analyser le signe de f prime prime, qui dépend de la valeur de A. Si A est positif, la fonction est concave, alors que si A est négatif, elle est convexe. Une erreur courante est de ne pas distinguer les différents cas. L'exercice demande également d'appliquer ce résultat à un exemple spécifique.

On redécouvre le log ?!

Le cours porte sur la fonction LN et sa relation fonctionnelle. Il s'agit de déterminer les fonctions satisfaisant l'équation f2ab = f2a + f2b et f'(1) = 1. En utilisant la dérivée du log, on démontre que si la fonction est non nulle et définie en 0, alors elle est égale à zéro partout. On conclut donc que la fonction ne peut pas être définie en 0. Ensuite, on démontre que f(1) = 0 en utilisant la relation fonctionnelle. On établit également que f(x/y) = f(x) - f(y) en s'inspirant de la démonstration de log(a/b) = log(a) - log(b). Enfin, on détermine le sens de variation de f sur (0, +∞) en utilisant la dérivée f'(x) = 1/x. On conclut en disant qu'en partant de ces deux propriétés, on peut retrouver toutes les propriétés du log et définir fondamentalement la fonction LN.

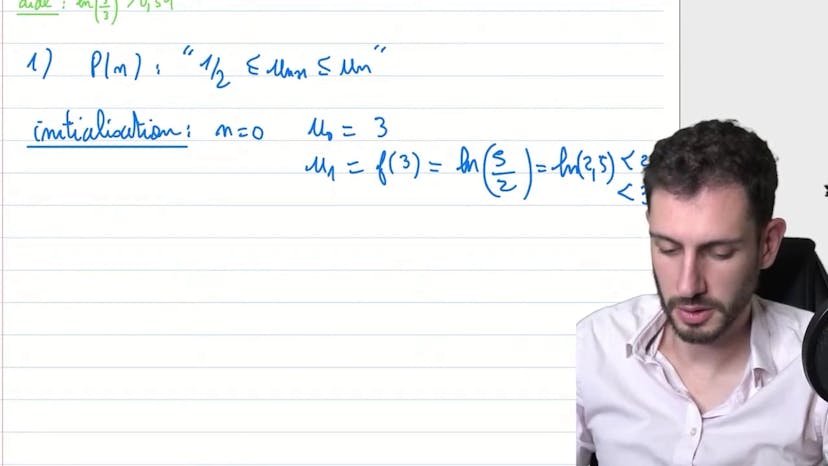
Fonction et suite récurrente associée

Dans ce cours, nous étudions une fonction définie par une fraction rationnelle avec un degré de 1 au-dessus et en-dessous de la barre de fraction. La fonction est définie sur l'intervalle de 0 à l'infini. Nous déterminons la limite de la fonction lorsque x tend vers l'infini et interprétons graphiquement cette limite comme un plateau atteint par la fonction à mesure que x tend vers l'infini. Ensuite, nous démontrons que la dérivée de la fonction est égale à une expression donnée pour tout nombre réel positif ou nul. Nous utilisons des transformations mathématiques pour simplifier le calcul de la dérivée. Nous concluons en disant que la fonction est strictement croissante et positif sur son ensemble de définition. Dans la deuxième partie du cours, nous étudions une suite définie par récurrence à l'aide de la fonction précédemment étudiée. Nous démontrons par récurrence que la suite est décroissante et minorée. Nous utilisons des calculs numériques pour vérifier l'initialisation de la récurrence et la propriété héréditaire. Enfin, nous concluons en disant que la suite converge vers une limite strictement positive en utilisant le théorème des suites décroissantes et minorées.

Une nouvelle définition de l'exp

Ce cours traite de sujets techniques et avancés en mathématiques, en particulier de la propriété du logarithme et de sa relation avec les puissances. Il explique comment utiliser le logarithme pour simplifier des expressions complexes avec des puissances et démontre une propriété importante du logarithme. L'objectif est de montrer que lorsque N tend vers l'infini, l'expression 1 + A/N^N converge vers l'exponentielle de A. Ce résultat est démontré en utilisant des propriétés du logarithme et de l'exponentielle, ainsi que des formules connues. En conclusion, le cours montre comment utiliser le logarithme pour simplifier et résoudre des problèmes de limite en mathématiques.