Online Learning Courses

Au choix : avec ou sans coordonnées ?

Dans ce cours, on apprend à résoudre un problème de géométrie avec des produits scalaires de deux manières : avec un système de coordonnées ou en utilisant la géométrie pure. La résolution avec coordonnées est très simple : on donne les coordonnées de tous les points et on calcule les coordonnées des vecteurs DE et AF pour démontrer que DE et AF sont perpendiculaires en appliquant la formule du produit scalaire. En revanche, la résolution sans coordonnées est un peu plus complexe : il faut réfléchir à comment décomposer DE et AF. En fin de compte, il faut développer le produit scalaire de DA plus AE et AB plus BF pour arriver à la conclusion que DE est orthogonal à AF. Même si la résolution sans coordonnées peut être plus créative, elle est souvent moins intuitive que la résolution avec coordonnées.

Caractériser un rectangle

In this video transcription, the goal is to prove that BA dot BC equals one quarter of (BD squared minus AC squared), where BCD is a parallelogram with a center at point H. The speaker initially tries to approach the problem from both sides but finds that it doesn't work well. Instead, they recommend starting from the left side and trying to simplify as much as possible, then doing the same for the right side, and finally comparing the two to see if they can be shown to be equal. The speaker also notes that the fact that H is the center of the parallelogram is important and should be used. By treating BD squared minus AC squared as a scalar function of AC, the speaker is able to simplify the expression to 4 times BO squared minus AO squared, which can then be compared to BO squared minus AO squared plus OC squared minus OA squared. Finally, it is shown that if BA dot BC equals 0, then BD equals AC, proving that ABCD is a rectangle. The main takeaway from this video is the method of approaching a problem from both sides and simplifying as much as possible before comparing the two expressions.

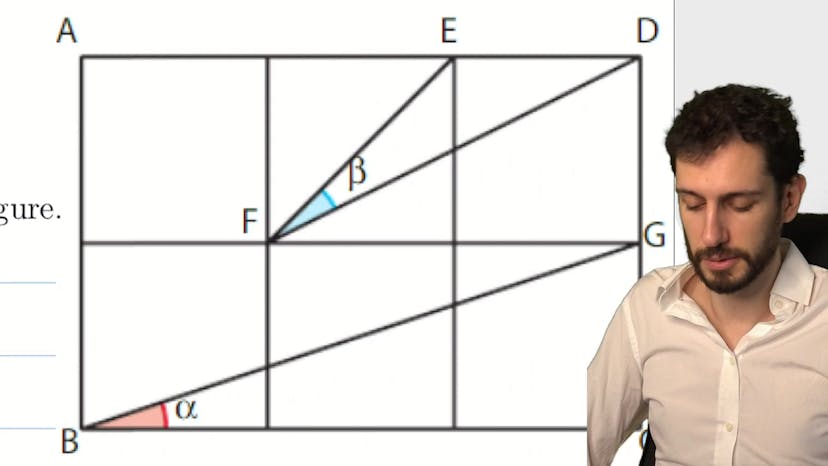
Comparer des angles : quelle formule appliquer ?

Dans cet exercice, il faut comparer les valeurs des angles alpha et beta d'une figure composée de 6 carrés de côté 1. Pour trouver les valeurs des angles, on peut utiliser le théorème d'Al-Kashi qui permet de calculer la mesure d'un côté en fonction des deux autres côtés et de l'angle correspondant. Pour alpha, on peut facilement accéder au cosinus en utilisant un triangle rectangle. Pour beta, on doit utiliser un triangle quelconque et appliquer Al-Kashi pour calculer la valeur de cos beta. Ensuite, il suffit de comparer les valeurs de cos alpha et cos beta pour déterminer lequel des deux angles est plus grand. On peut remarquer que les deux angles sont entre 0 et pi sur 2, ce qui permet de dire que si alpha est plus grand que beta, alors cos alpha est plus petit que cos beta. En résolvant l'exercice, on trouve que cos alpha et cos beta sont égaux, donc alpha = beta. L'exercice permet de tester notre utilisation du théorème d'Al-Kashi et notre réflexe pour résoudre des problèmes avec des angles bizarres.

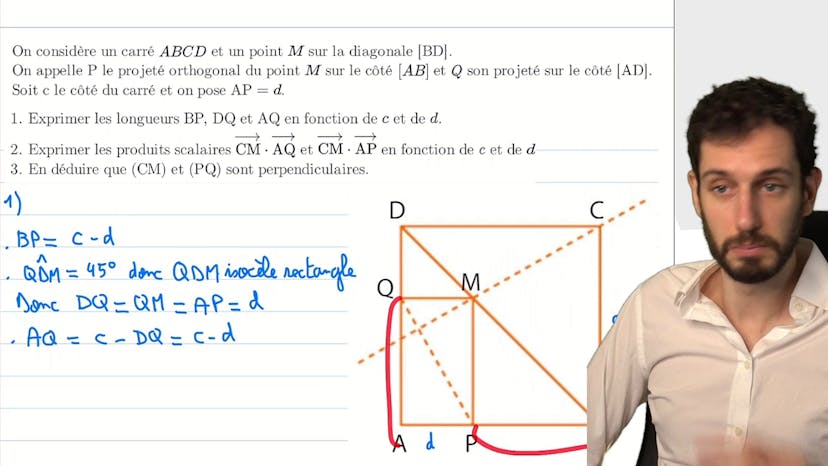
Améliorer sa géométrie sans coordonnées

Dans cet exercice de géométrie, on prend un carré ABCD et un point M sur la diagonale BD. On doit démontrer que la droite CM et la droite PQ sont orthogonales. Si on utilisait des coordonnées, cela pourrait être facile, mais on nous guide sur comment faire une démonstration géométrique à l'aise. On exprime les longueurs BP, DQ, AQ en fonction de C et D, puis les produits scalaires CM.scalar AQ et CM.scalar AP. En décomposant le vecteur CM en CD, DQ et QM, on peut montrer que CM.scalar AQ est égal à DQ.scalar AQ et CM.scalar AP est égal à moins C.scalar D plus la norme de QM. On en déduit que CM et PQ sont perpendiculaires. Pour résoudre des exercices de géométrie avec des produits scalaires et des vecteurs penchés, il est utile de décomposer les vecteurs en utilisant exclusivement des angles droits.

Encore plus loin sur les ensembles de points et les milieux

Dans cet exercice, nous devons déterminer l'ensemble des points M tel que M à scalaire MB est égal à 3, où AB est de longueur 2 et I est le milieu de AB. Pour résoudre l'exercice, nous utilisons la formule M à scalaire MB = MI² - 1/4 AB². Nous isolons ensuite MI² pour obtenir MI = 2. Ainsi, nous concluons que l'ensemble de points M est un cercle de centre I et de rayon 2.Dans la deuxième question, nous devons exprimer MA² + MB² en fonction de MI, étant donné que I est le milieu de AB. Nous utilisons la formule MA² + MB² = 2MI² + AB²/2 pour résoudre l'exercice. Nous comparons ensuite les ensembles obtenus dans les deux questions et constatons qu'ils sont identiques.Cette méthode est utile pour simplifier des expressions avec du M grâce au produit scalaire, en particulier lorsque le milieu d'un segment est impliqué. En appliquant cette méthode, on peut enlever des morceaux d'une expression qui sont communs aux deux points et obtenir une expression beaucoup plus compacte.

Analyse

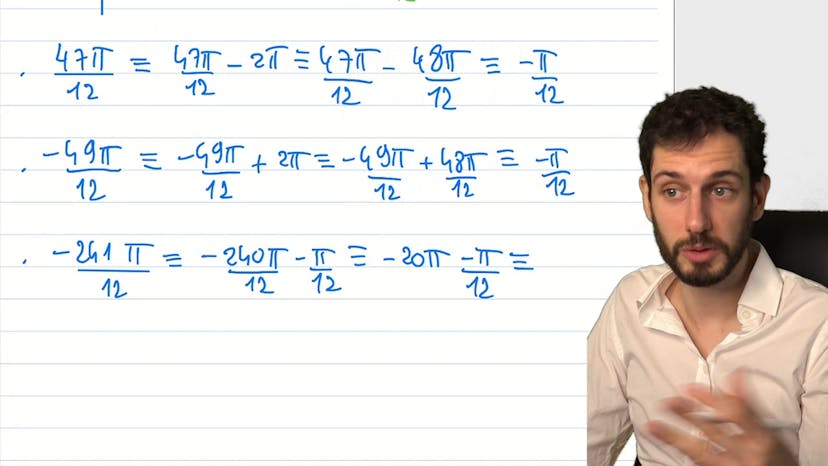
Point 1 : Mêmes mesures sur le cercle trigo

Le cours explique comment fonctionne le placement des angles sur le cercle trigonométrique. Chaque point du cercle correspond à plusieurs valeurs de longueur d'arc de cercle. Il est alors possible d'enlever des paquets de 2pi pour retrouver la mesure fondamentale ou la plus petite. Le cours présente plusieurs exemples pour aider à comprendre le concept et invite les étudiants à s'entraîner à enlever ces paquets pour retrouver la mesure souhaitée.

Analyse

Point 2 : Calcul de certains sin et cos grâce au cercle

Ce cours explique comment connaître les valeurs de pi sur 6, pi sur 3, pi sur 4, pi sur 2 en utilisant les valeurs de sine et de cos, et comment trouver des valeurs approchantes en utilisant des symétries sur le cercle. Il est important de mémoriser les valeurs canoniques de sine et de cos pour les utiliser efficacement. Cette méthode est simple et efficace pour lire les angles et éviter d'apprendre des centaines de valeurs.

Analyse

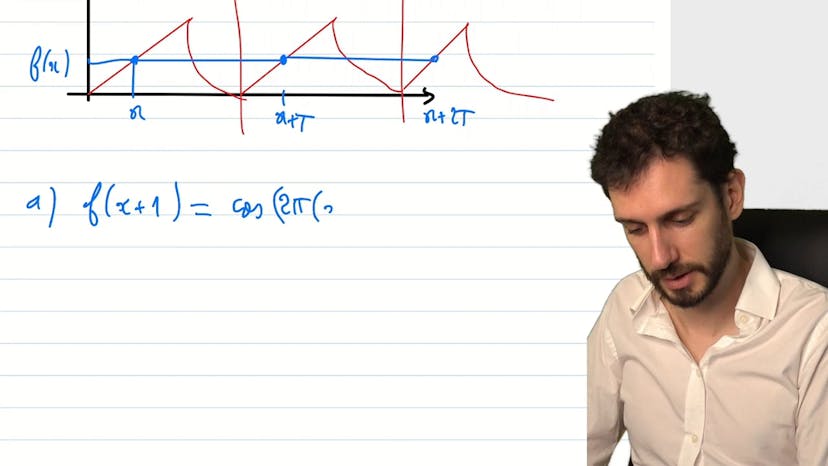
Point 3 : les fonctions périodiques

Une fonction périodique se caractérise par la répétition d'un motif de taille fixe appelé la période. Mathématiquement, cela signifie que pour tout nombre de périodes ajoutées, la valeur de la fonction reste la même. Pour vérifier qu'une fonction est périodique, il suffit de vérifier que f(x+T) = f(x) pour une période T donnée. Les fonctions sinus et cosinus sont périodiques de période 2π, ce qui permet de résoudre certains exemples en trouvant une période commune.

Point 1 : définition vecteur normal

This lesson is about finding the direction and normal vectors of a line, and then using them to determine the equation of a perpendicular line passing through a given point. The example in the lesson shows step-by-step how to find the direction vector of a line, as well as the equation of a perpendicular line passing through a given point. The lesson emphasizes the importance of making a quick sketch to better visualize the problem being solved. By following the fundamental definitions taught in this lesson, one can find equations for lines in a straightforward manner.

Trouver une droite à partir d'un vecteur normal

Dans ce cours, nous apprenons comment trouver l'équation d'une droite en connaissant un point et un vecteur normal. La première étape consiste à utiliser le vecteur normal pour trouver la forme générale de l'équation, qui est de la forme ax+by+c=0. Ensuite, nous utilisons le point donné pour calculer la constante c. En résolvant cette équation, nous pouvons trouver l'équation finale de la droite. Dans cet exemple, la droite est représentée par moins 2x plus 4y plus 6 égale zéro, qui peut également être écrite sous forme simplifiée de moins x plus 2y moins 3 égale zéro.

Utiliser vecteur directeur ET vecteur normal

This lesson covers how to find both the direction and normal vectors of a given line, and then how to use them to calculate a new line perpendicular to the first passing through a given point. A vector "-b-a" can be used as a direction vector, with a being the coefficient before y. The normal vector can be found from the Cartesian equation of the line through "-b-a". To find the equation of a new line perpendicular to the first, a direction vector can be used as a normal vector for the new line. The equation can then be found by applying the standard formula, using a known point on the new line to solve for the constant. Finally, the reduced equation can be found by isolating for the y variable.