Online Learning Courses

PGCD et n carré

Aucun résumé n'est disponible pour cette vidéo

Dans cet exercice, on doit trouver deux nombres et manipuler le PGCD et le PPCM. On sait que A est plus petit que B, leur PGCD vaut 6 et leur PPCM vaut 102. En utilisant une formule qui relie le produit de deux nombres au produit de leur PGCD et PPCM, on peut trouver A' et B' tels que A est 6 fois A' et B est 6 fois B', et A' et B' sont premiers entre eux. En simplifiant cette formule, on obtient A'B' est égal à 17, donc A' vaut 1 et B' vaut 17. A est donc 6 et B est 102.

PGCD et congruences

Dans cet exercice de mathématiques, nous manipulons le PGCD et des congruences. Le système S établit que n est congruent à 1 modulo 5 et à 5 modulo 7. Nous devons montrer que si n vérifie le système S, alors il vérifie également un autre système. Nous montrons cela en utilisant des congruences et en utilisant le corollaire du théorème de Gauss. Nous en déduisons que 4n est congruent à moins 1 modulo 35, et en résolvant cette équation, nous obtenons que l'ensemble des solutions est {26 + 35k | k ∈ Z}.

PGCD et Suite

Dans cet article, nous étudions un exercice sur le PGCD et les suites. Nous avons une suite définie sur n, avec u0 = 0 et u1 = 1, et une relation de récurrence. Nous avons également une autre suite, vn, définie comme étant un + 1 - un. Nous montrons que vn est une suite géométrique de raison 2 et que le terme initial v0 est égal à 1. Nous déduisons ensuite que pour tout entier n, un est un entier naturel et que un + 1 est égal à 2 fois un + 1. Nous utilisons ensuite une somme télescopique pour montrer que un est un entier. Enfin, nous utilisons le théorème de Bézout pour montrer que deux termes consécutifs de la suite sont premiers entre eux.

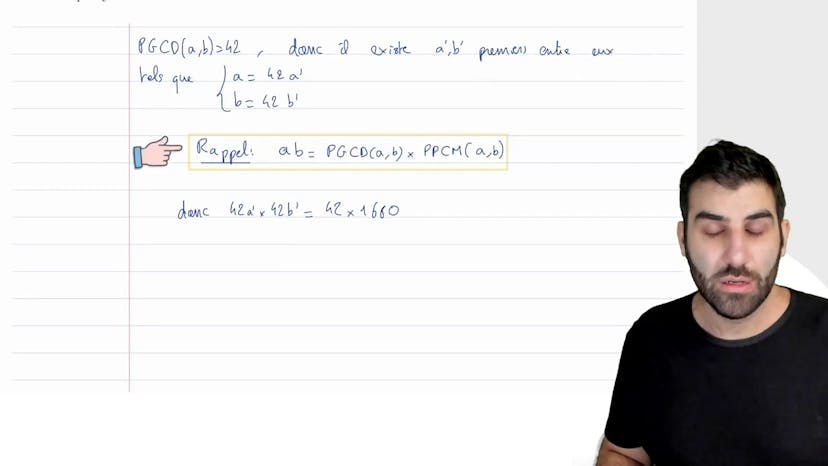
PGCD+PPCM

Dans cet exercice, on cherche un couple A et B qui ont un PGCD de 42 et un PPCM de 1680. On utilise une méthode où l'on extrait des diviseurs premiers de A et de B qui sont premiers entre eux, puis on simplifie l'équation en utilisant une formule qui relie le PGCD et le PPCM. Après simplification, on obtient que A'B' est égal à 40, et en excluant les diviseurs de 40 qui ne sont pas premiers entre eux, on obtient les deux possibilités suivantes : A est égal à 42 et B est égal à 1680 ou A est égal à 210 et B est égal à 336. Ces sont toutes les solutions du système d'équations avec le PGCD et le PPCM.

Récurrence et coeff binomiaux

Dans cette vidéo, Mathis de Studio explique comment démontrer que la somme pour k allant de p à n, de p parmi k, est égale au binôme de Newton, p plus 1 parmi n plus 1. Il utilise la méthode de la récurrence pour montrer que cette propriété est vraie pour tout n appartenant à n. Il utilise également le triangle de Pascal pour trouver des relations entre les différents binômes successifs. La clé de l'exercice est l'analyse avant, ce qui permet de déterminer une méthode claire pour résoudre l'exercice.

Inégalité de Cauchy Schwarz

Dans cette vidéo, Mathis de Studio démontre deux inégalités classiques pour n antinaturel non nul et deux suites de réels, a_i et b_i. Il montre que, pour la somme pour k allant de 1 à n des a_k b_k, la valeur absolue est inférieure ou égale à la somme pour k allant de 1 à n des valeurs absolues de a_k valeurs absolues b_k, ce qui est inférieur ou égal à la racine carrée de la somme pour k allant de 1 à n des a_k², multipliée par la racine carrée de la somme pour k allant de 1 à n des b_k². Il utilise un polynôme f(x) pour montrer que, dans les deux cas examinés, l'inégalité est vérifiée. En conclusion, la valeur absolue de la somme des a_k b_k est inférieure ou égale à la somme des valeurs absolues de a_k valeurs absolues b_k, qui est inférieure ou égale à la racine carrée de la somme des a_k², multipliée par la racine carrée de la somme pour k allant de 1 à n des b_k².

Série harmonique

Dans cet exercice sur la série harmonique, il est important de maîtriser la première étape qui montre comment la série diverge. Ensuite, nous étudions l'écart entre la série harmonique et ln(2n+1), qui converge vers une constante appelée "gamma". Pour arriver à ce résultat, nous utilisons une comparaison de série intégrale et nous encadrons l'intégrale de 1/x entre deux aires de rectangle. Pour prouver rigoureusement cette méthode, nous utilisons la stricte décroissance de la fonction 1/x. Ensuite, nous étudions les suites h(n)-ln(n) et h(n)-ln(n+1), et nous prouvons que ces suites convergent vers la même limite gamma. Nous montrons que gamma appartient à l'intervalle [1,5;1], et nous trouvons sa valeur grâce à la calculatrice ou au tableur. Enfin, nous résolvons une équation pour trouver à partir de quelle valeur de n un moins la suite vn sera inférieure à 10,2, ce qui nous permet de conclure que cette méthode est efficace. La première étape est essentielle et doit être maîtrisée sans hésitation.

Suite arithmético géométrique

Les suites arithmético-géométriques sont un cas particulier des suites définies par récurrence. Si la suite est définie par une relation "un+1 = ax+b" avec "a" différent de 1, alors il existe un point fixe "l=b/(1-a)" qui est la seule limite possible de la suite. Pour déterminer si la suite converge, on introduit une suite auxiliaire "vn=un-l", qui, si la suite converge, est géométrique de raison "a". Si "a" est supérieur à 1 en valeur absolue, la suite diverge vers plus infini, sauf si la valeur initiale est égale à 0. Si "a" est égal à moins 1, la suite oscillera entre deux valeurs. Si "a" est inférieur à 1 en valeur absolue, la suite converge vers "l". En application à un carré divisé en neuf carrés, si le carré central est colorié et que pour chaque étape on colore le carré central de chaque carré restant, le carré finira entièrement colorié. Retenez la méthode du point fixe et de la suite auxiliaire pour maîtriser les suites arithmético-géométriques.

Sommes doubles

Dans cette vidéo, Mathis de Studio enseigne comment calculer des sommes doubles. Pour toute somme double, la méthode consiste à la dédoubler en deux sommes simples, c’est-à-dire à fixer un des deux indices pour permettre de calculer la somme sur un seul indice au lieu de deux. Pour la première somme donnée, il s’agit de la somme pour i et j de 1 à n de i + j au carré. En dédoublant cette somme, on obtient deux sommes simples, la première pour i allant de 1 à n des sommes pour j allant de 1 à n de 1 + j au carré, et la deuxième pour j allant de 1 à n des sommes pour i allant de 1 à n de 1 + i au carré. En utilisant les formules classiques de somme des carrés et de somme des entiers, on obtient que la somme initiale est égale à n*(n+1)*(7n+5)/6. Pour la deuxième somme donnée, il s’agit de la somme pour i plus grand que i mais plus petit que j strictement, et j qui est plus petit que n, des i fois j. En fixant j et en utilisant une formule classique, on obtient que cette somme est égale à n*(n+1)*(3n²-n-2)/24.Pour la troisième somme donnée, il s’agit de la somme pour i et j de 1 à n du minimum de i et j. En séparant cette somme en deux sommes, une pour laquelle j est plus grand que i et l’autre pour laquelle j est plus petit que i, on obtient que cette somme est égale à n*(n+1)*(2n+1)/6.Enfin, pour la quatrième somme donnée, il s’agit de la somme pour i plus grand que 1, plus petit que j, plus petit que n, des i divises par j. En sortant j en premier, on peut obtenir que cette somme est égale à n*(n+3)/4.

Equation fonctionnelle

Dans cette vidéo, l'objectif est de résoudre une équation fonctionnelle. On nous demande de trouver toutes les fonctions continues de 0,1 dans R qui vérifient pour tout x appartenant à 0,1 f de x sur 2 plus f de x plus 1 sur 2 est égale à 3 f de x. Pour démarrer, le speaker teste différentes fonctions classiques. Il montre que f égale à 0 fonctionne et décide alors de prouver par l'absurde que f ne peut être égal qu'à 0. Après avoir montré que f est bornée et atteint ses bornes, il utilise la supposition par l'absurde pour montrer que f ne peut être égal qu'à 0. La preuve est simple, le maximum ou le minimum de f doit être différent de 0, sinon f serait égale à 0. S'il est différent de 0, cela mène à une contradiction, montrant ainsi que f doit être égal à 0.