 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
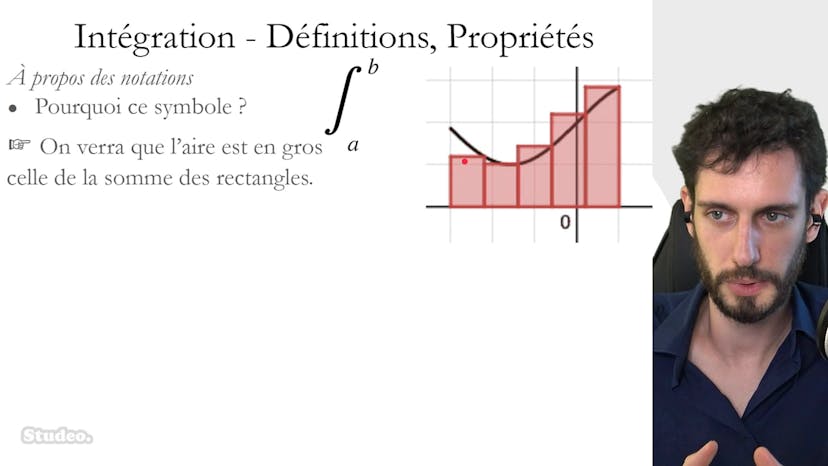
Introduction
Dans cette vidéo d'introduction sur les intégrales, nous allons présenter les définitions et les propriétés de l'intégrale. Tout au long du chapitre, nous allons calculer des R sous des courbes. Dans ce sous-chapitre, nous posons les bases pour les fonctions continues et nous examinons les fonctions positives et négatives.
Nous commençons par un exemple simple. Si nous avons une fonction constante avec une hauteur de 2 et une plage de 0 à 3, l'R sous la courbe est égal à 6, ce qui est représenté par un rectangle de largeur 3 et de hauteur 2. Nous pouvons faire la même chose avec une fonction affine de pente 1, qui est représentée par un triangle rectangle isocèle avec une base de 3 et une hauteur de 3. L'R est donc égal à 9 demi (9/2).
Vous pourriez vous demander pourquoi consacrer un chapitre à cela. En réalité, nous aurons des fonctions plus complexes et nous utiliserons cette approximation simple du rectangle pour comprendre comment fonctionne l'R sous une fonction plus courbe et complexe. Ainsi, nous pourrons dire que cela équivaut à l'R d'une somme de rectangles, du moins approximativement. Les rectangles auront une largeur (delta x) et une hauteur (f de x) en fonction du point considéré.
Pour être plus précis, ce symbole "S" stylisé représente une somme entre a et b. L'R est essentiellement égal à la somme des rectangles lorsque le nombre de rectangles devient infini, c'est-à-dire lorsque la somme atteint une R complète plutôt qu'une approximation. Nous utilisons également la notation "dx" pour représenter une largeur infiniment petite lorsque le nombre de rectangles devient très grand.
Dans ce sous-chapitre, nous allons aborder les définitions de l'intégrale pour les fonctions continues positives et les fonctions de signes quelconques. Nous utiliserons des encadrements et des intuitions graphiques pour estimer les intégrales. Les méthodes abordées seront le calcul de l'R et l'estimation de l'intégrale à l'aide de rectangles.
Bon courage pour ce chapitre, et je vous retrouve dans la prochaine vidéo. N'hésitez pas à poser vos questions dans la FAQ, et à bientôt !
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Définition de l'intégrale
L'intégrale d'une fonction continue et positive sur un intervalle a, b correspond à l'aire sous la courbe de cette fonction entre les valeurs a et b, ainsi que l'axe horizontal. On peut également l'appeler le domaine sous la courbe ou l'aire sous la courbe. L'unité utilisée pour mesurer cette aire est l'unité d'air, qui est un petit carré de taille 1 sur 1 dans un repère orthonormé. On note l'intégrale comme une expression mystérieuse "intégrale entre a et b de f de x, dx". Cette définition peut être étendue aux fonctions négatives en calculant la surface correspondante et en lui attribuant un signe négatif. Dans certains cas, il peut y avoir des parties positives et des parties négatives de la fonction. Il est important de se rappeler que l'intégrale est positive lorsque la fonction est au-dessus de l'axe OX et négative lorsqu'elle est en dessous. N'hésitez pas à poser des questions supplémentaires dans la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Encadrement et intuition graphique
Dans cette vidéo, nous abordons différentes méthodes d'approximation de l'aire sous une courbe. Nous commençons par expliquer que lorsque la courbe est une droite, le calcul de l'aire est assez simple, en utilisant des formes géométriques comme des triangles ou des rectangles. Cependant, lorsque la courbe est incurvée, il devient plus compliqué de calculer l'aire.
Nous présentons donc les méthodes d'approximation suivantes : les rectangles supérieurs et inférieurs. Ces méthodes consistent à diviser l'intervalle en plusieurs petits intervalles de même amplitude, et à construire des rectangles inférieurs qui collent la courbe par en dessous, ainsi que des rectangles supérieurs qui collent la courbe par en dessus. Lorsque le nombre de rectangles tend vers l'infini et que leur taille diminue, les rectangles inférieurs et supérieurs convergent vers la vraie valeur de l'aire.
En plus de ces méthodes, nous mentionnons brièvement d'autres méthodes qui ne sont pas au programme, mais qui illustrent différentes possibilités : la méthode du point milieu et la méthode des trapèzes. La méthode du point milieu consiste à tracer des rectangles qui sont traversés par la courbe au milieu de leur côté supérieur, offrant ainsi une meilleure précision. La méthode des trapèzes permet quant à elle d'utiliser des quadrilatères non-rectangulaires, offrant ainsi plus de liberté pour se rapprocher de la courbe.
En conclusion, cette vidéo explicative présente les différentes méthodes d'approximation de l'aire sous une courbe, en mettant notamment l'accent sur les rectangles supérieurs et inférieurs.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
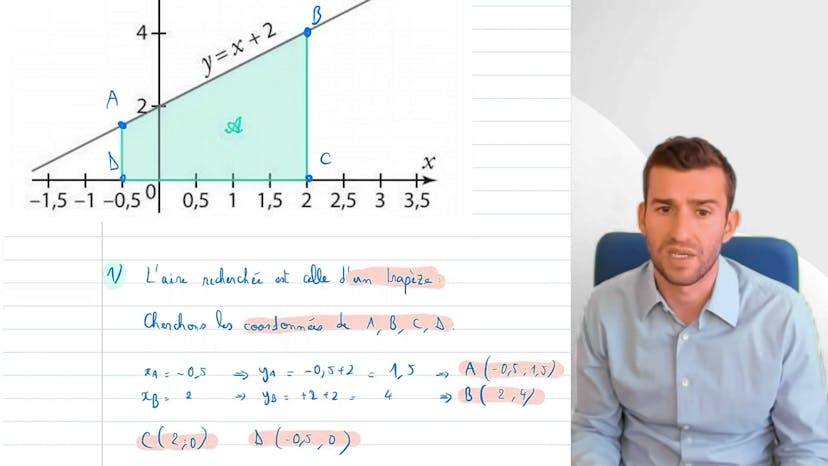
Intégrale et Aire
Lors de ce cours, nous apprenons comment calculer une intégrale de manière géométrique sans utiliser la fonction. Cela est possible lorsque la forme géométrique est simple, comme dans notre exemple avec une fonction affine.
Nous nous intéressons à l'intégrale de la fonction x plus 2 entre -0,5 et 2. Pour calculer cette intégrale, nous pouvons utiliser deux méthodes : calculer la primitive de x plus 2, ce qui est relativement simple, ou utiliser une forme géométrique connue pour calculer facilement l'erreur.
Dans ce cas, la forme géométrique est un trapèze, ce qui facilite le calcul. Pour cela, nous avons besoin de la hauteur, de la largeur et de la longueur des bases du trapèze. Nous trouvons les coordonnées des points a, b, c et d en utilisant les équations de la droite. Les coordonnées de a sont (-0,5, 1,5) et les coordonnées de b sont (2, 4). Les points c et d étant sur l'axe des abscisses, leurs coordonnées sont (2, 0) et (-0,5, 0) respectivement.
Nous calculons ensuite les différentes longueurs du trapèze en prenant la différence entre les ordonnées des deux points correspondants. Cela donne 1,5 pour la longueur a-d, 4 pour la longueur b-c et 2,5 pour la longueur d-c.
En appliquant la formule de l'aire du trapèze, qui est la moyenne des deux bases multipliée par la hauteur, nous obtenons l'aire du trapèze. Dans notre cas, cela donne 1,5 * (1,5 + 4) * 2,5, soit 6,875.
Cette méthode permet de calculer une intégrale en utilisant directement l'aire géométrique du trapèze, sans avoir besoin de calculer les primitives. Il suffit de trouver les coordonnées des points et de calculer les longueurs et l'aire du trapèze.
Cela conclut notre méthode de calcul d'une intégrale à l'aide d'une forme géométrique.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
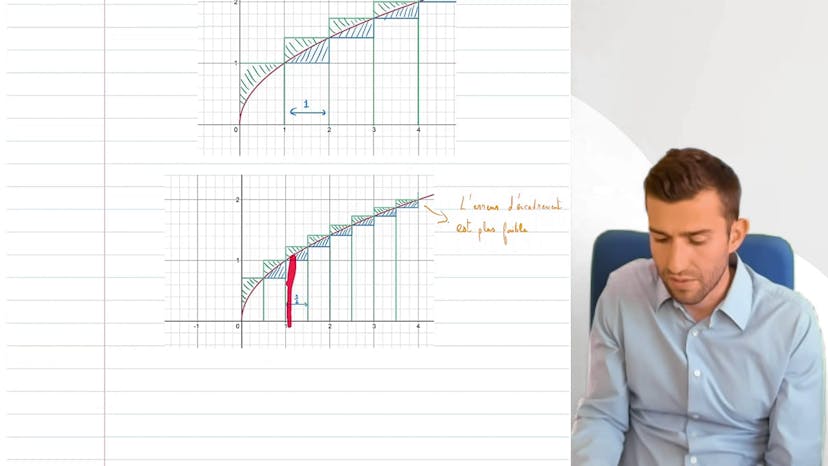
Méthode des Rectangles
Dans ce cours, nous apprenons à calculer une aire géométrique à l'aide de la méthode des rectangles. La courbe intégrée n'a pas une forme géométrique simple, donc nous ne pouvons pas calculer l'aire de manière directe. Cependant, nous pouvons encadrer cette aire en utilisant des petits rectangles en dessous de la courbe et des grands rectangles au-dessus. En diminuant la largeur des rectangles, nous affinons notre encadrement et nous tendons vers l'aire recherchée, c'est-à-dire l'intégrale.
Nous cherchons donc à encadrer l'aire sous la courbe de la fonction de 0 à 4. La fonction est croissante, donc nous encadrons l'aire en utilisant les rectangles a'0, a'1, a'2 et a'3. Les a'0, a'1, a'2 et a'3 se calculent en multipliant la largeur par la hauteur de chaque rectangle. Par exemple, a'1 est égal à 1 fois 1 (largeur fois hauteur), ce qui donne 1.
En utilisant ces calculs, nous obtenons l'encadrement 1 plus racine de 2 plus racine de 3 pour l'aire sous la courbe, et 3 plus racine de 2 plus racine de 3 pour l'encadrement formé par les petits rectangles.
Pour augmenter la précision de l'encadrement, nous pouvons utiliser des rectangles de largeur plus petite, comme 1,5, 1,25, etc. En faisant tendre la largeur vers zéro, nous obtenons des rectangles qui collent de plus en plus à la courbe et ainsi un encadrement plus précis.
En résumé, la méthode des rectangles permet d'encadrer l'intégrale lorsque nous ne pouvons pas trouver une primitive de la fonction. Il est possible d'améliorer la précision de l'encadrement en utilisant des rectangles de plus en plus petits.
Révisions Maths lycée
Analyse Terminale
BCPST

Introduction
Cette vidéo d'introduction présente le premier topic du chapitre sur les intégrales. L'auteur explique que l'objectif du chapitre est de calculer des R sous des courbes. Dans ce sous-chapitre, des bases sont posées pour les fonctions continues, positives et négatives. Des exemples simples sont utilisés pour illustrer les concepts, tels qu'un rectangle avec une hauteur de 2 et une longueur de 3, dont l'R sous la courbe est de 6. Un autre exemple est un triangle rectangle isocèle avec une base de 3 et une hauteur de 3, dont l'R est égal à 9 demi.
Ensuite, l'auteur explique que même si ces exemples semblent simples, ils sont importants car ils servent d'approximation pour comprendre le concept d'R sous des fonctions plus complexes. Il explique que l'R peut être approximativement égal à la somme des rectangles, avec une largeur de delta x (distance entre les deux points) et une hauteur de f de x (selon le niveau de la fonction). Cependant, l'R est égal à la somme des rectangles uniquement lorsque cette somme est effectuée sur un nombre infini de rectangles.
L'auteur utilise le symbole S stylisé pour représenter cette somme infinie. Il explique que cette somme infinie permet d'approcher la vraie valeur de l'R. Lorsque le nombre de rectangles devient très grand, on utilise la notation dx pour représenter la largeur infiniment petite des rectangles. L'auteur souligne que cette somme infinie est représentée par le symbole S stylisé.
En conclusion, l'auteur résume les points importants de ce sous-chapitre, qui incluent la définition de l'intégrale pour les fonctions continues positives et les fonctions de signes quelconques. Les méthodes abordées sont le calcul de l'R et l'estimation de l'intégrale par la méthode des rectangles. L'auteur encourage les téléspectateurs à poser des questions dans la FAQ et les remercie pour leur attention.
Révisions Maths lycée
Analyse Terminale
BCPST

Définition de l'intégrale
L'intégrale d'une fonction continue et positive sur un intervalle a, b correspond à l'aire sous la courbe de cette fonction entre les axes verticaux x = a, x = b et l'axe horizontal. Elle peut également être appelée "domaine sous la courbe" ou "surface sous la courbe" et est exprimée en unité d'aire. L'unité d'aire est définie comme étant le petit carré de taille 1 entre 0i et 0j dans un repère orthonormé. L'intégrale est notée sous la forme d'un signe mystérieux "∫" suivi de la fonction f(x) et de "dx" pour indiquer la variable d'intégration. Si la fonction f est négative, l'intégrale sera évaluée avec un signe négatif pour représenter une surface négative. Dans certains cas, il peut y avoir des parties positives et négatives, où chaque partie sera évaluée séparément. Il est important de noter que l'intégrale est positive lorsque la fonction est au-dessus de l'axe horizontal et négative lorsqu'elle est en-dessous.
Révisions Maths lycée
Analyse Terminale
BCPST

Encadrement et intuition graphique
Dans cette vidéo, nous abordons les différentes méthodes pour approximer l'aire sous une courbe. L'objectif est de mieux comprendre ce qu'est le calcul de l'aire.
Nous commençons par expliquer qu'il est facile de calculer l'aire lorsque la courbe est une droite en utilisant des formes géométriques simples telles que des triangles et des rectangles. Cependant, cela devient plus compliqué lorsque la courbe est incurvée.
Nous présentons ensuite la méthode des rectangles supérieurs et inférieurs, qui est la méthode principale étudiée. Cette méthode consiste à diviser l'intervalle en plusieurs petits intervalles de taille égale et à construire des rectangles inférieurs qui se collent en dessous de la courbe et des rectangles supérieurs qui se collent au-dessus.
Lorsque le nombre de rectangles augmente et leur taille diminue, ces rectangles se rapprochent de plus en plus de la courbe, se rapprochant ainsi de la vraie valeur de l'intégrale. Si la fonction est croissante, les aires des rectangles inférieurs et supérieurs sont classées dans un ordre croissant.
Nous illustrons ces concepts à l'aide d'un graphique montrant la fonction sinus croissante. Nous utilisons 6 rectangles pour approximer l'aire sous la courbe et montrons comment cette approximation s'améliore en augmentant le nombre de rectangles et en diminuant leur taille.
En plus des méthodes au programme, nous mentionnons également la méthode du point milieu et la méthode des trapèzes, qui offrent des approximations plus précises mais ne sont pas étudiées dans ce cours.
Nous concluons en résumant que ces méthodes d'approximation permettent de se rapprocher de la vraie valeur de l'intégrale et de mieux comprendre le calcul de l'aire. Si des questions subsistent, nous invitons les spectateurs à les poser dans la FAQ et nous annonçons une prochaine vidéo sur le sujet.
Révisions Maths lycée
Analyse Terminale
BCPST

Intégrale et Aire
Dans ce cours, nous apprenons comment calculer une intégrale géométriquement, sans utiliser de fonction. Cela fonctionne lorsque la forme géométrique est simple, comme dans ce cas avec une fonction affine. L'erreur d'intégration est représentée par un trapèze, ce qui facilite le calcul.
Nous nous intéressons ici à l'intégrale de la fonction x plus 2 entre -0,5 et 2. L'intégrale correspond à l'erreur sous la courbe par rapport à l'axe des abscisses. Nous devons calculer cette partie. Il existe deux méthodes : soit on calcule la primitive de x plus 2 et on procède au calcul habituel, soit on reconnaît une forme géométrique et on utilise la méthode géométrique. Dans ce cas, il s'agit d'un trapèze, donc nous devons trouver sa hauteur, sa largeur et la longueur de ses bases.
Pour cela, il est préférable de trouver les coordonnées des points a, b, c et d. Les points a et b appartiennent à la droite et vérifient son équation, connaissant les abscisses -0,5 et 2. Les coordonnées de a sont donc -0,5 et 1,5, et celles de b sont 2 et 4. Les points c et d se trouvent sur l'axe des abscisses, donc leurs coordonnées sont respectivement 2,0 et -0,5,0.
Ensuite, nous calculons les différentes longueurs du trapèze. Comme elles sont soit horizontales, soit verticales, cela est relativement simple. La longueur a-d est la différence entre les deux ordonnées, soit 1,5. Pour b-c, c'est 4. Et pour d-c, c'est 2,5.
En appliquant la formule de l'aire du trapèze (la moyenne des deux bases fois la hauteur d), nous obtenons l'aire du trapèze, qui est de 6,875. Notez que la formule peut varier selon la définition des bases et de la hauteur, mais elle implique la moyenne des côtés parallèles ayant des longueurs différentes fois la base.
Ainsi, dans ce cas particulier, nous n'avons pas besoin de calculer la primitive de la fonction. Nous pouvons directement calculer l'aire géométrique du trapèze pour obtenir l'intégrale. Cela montre une méthode alternative pour le calcul des intégrales.
Révisions Maths lycée
Analyse Terminale
BCPST

Méthode des Rectangles
Ce cours traite de la méthode d'encadrement pour calculer une intégrale. L'objectif est d'estimer l'aire sous une courbe qui n'a pas une forme géométrique simple en utilisant la méthode des rectangles. Cette méthode consiste à encadrer l'aire totale par l'aire des petits rectangles situés en dessous de la courbe et par l'aire des grands rectangles situés au-dessus de la courbe. En diminuant la largeur des rectangles, on affine progressivement l'encadrement et on tend vers l'intégrale recherchée. Cette méthode est appelée l'intégrale de Riemann.
Dans cet exemple, on cherche à encadrer l'aire sous la courbe d'une fonction croissante entre 0 et 4. On divise l'intervalle en petits rectangles et on calcule l'aire de chacun en multipliant la largeur par la hauteur. En utilisant la fonction racine carrée, on obtient les aires des différents rectangles : a'1 = 1, a'2 = √2, a'3 = 2. On peut ensuite encadrer l'intégrale en additionnant ces aires : 1 + √2 + √3 < intégrale < 3 + √2 + √3. Cet encadrement n'est pas très précis car il y a une différence de 2 entre les bornes supérieure et inférieure. En augmentant la précision en utilisant des rectangles de largeur plus petite (par exemple, 1,5 au lieu de 1), on obtient un encadrement plus fin qui se rapproche davantage de l'intégrale réelle.
En résumé, la méthode d'encadrement permet d'estimer l'intégrale d'une fonction en utilisant la somme des aires des rectangles situés en dessous et au-dessus de la courbe. En affinant la précision en diminuant la largeur des rectangles, on obtient un encadrement de plus en plus précis de l'intégrale. C'est une méthode utile lorsque l'on ne peut pas trouver une primitive de la fonction.
Révisions Maths lycée
Analyse Terminale
ECG

Introduction
Bienvenue dans cette vidéo d'introduction au premier topic du chapitre sur les intégrales. Dans cette vidéo, nous présentons les définitions et les propriétés des intégrales. Dans ce chapitre, nous allons calculer des aires sous des courbes, c'est-à-dire trouver l'intégrale d'une fonction continue. Nous commençons par poser les bases pour les fonctions continues, positives, négatives, etc.
Pour illustrer ces concepts, nous prenons un exemple simple de calcul de l'aire sous la courbe d'une fonction constante égale à 2 entre 0 et 3. L'aire sous cette courbe est un rectangle de hauteur 2 et de largeur 3, donc l'aire est de 6. Nous faisons également le même calcul avec une fonction affine de pente 1, et nous obtenons un triangle rectangle isocèle avec une base de 3 et une hauteur de 3. L'aire sous cette courbe est donc de 9/2.
Vous pouvez vous demander pourquoi consacrer un chapitre à ce sujet. En réalité, nous aurons des fonctions plus complexes et nous nous inspirerons de l'approximation du cas simple du rectangle pour comprendre le calcul de l'aire sous une fonction courbe. Nous pourrons dire que cela est approximativement égal à l'aire d'une somme de rectangles. Les rectangles auront une largeur delta x pour la distance entre les deux points et une hauteur égale à la valeur de la fonction f(x) à chaque point.
Pour être plus précis, cette approximation est valable lorsque nous faisons une somme sur un nombre infini de rectangles, c'est-à-dire lorsque nous rendons la largeur des rectangles infiniment petite. En notation mathématique, nous utilisons donc le symbole de la somme stylisé, qui représente la somme entre a et b.
Les points importants de ce sous-chapitre seront la définition de l'intégrale pour les fonctions continues positives et pour les fonctions de signes quelconques, ainsi que l'encadrement et l'intuition graphique. Les méthodes que nous utiliserons seront le calcul de l'aire par un R, suivi de l'estimation de l'aire par la méthode du rectangle.
En conclusion, ce cours introduit les concepts et les approximations de calcul des intégrales. Nous vous souhaitons bon courage pour la suite du chapitre et nous vous retrouverons dans la prochaine vidéo. N'hésitez pas à poser des questions dans la FAQ si besoin. À bientôt !
Révisions Maths lycée
Analyse Terminale
ECG

Définition de l'intégrale
L'intégrale d'une fonction continue et positive sur un intervalle [a, b] représente l'aire sous la courbe de cette fonction entre les valeurs de x égales à a et b, ainsi que l'axe horizontal. On peut également l'appeler "aire sous la courbe de f sur l'intervalle [a, b]". L'unité d'aire utilisée peut varier en mathématiques, mais on utilise généralement un carré de taille 1 sur 1 comme unité d'aire. L'intégrale est notée "∫f(x) dx", c'est-à-dire le symbole mystérieux que l'on découvre en mathématiques.
Si la fonction f(x) est négative sur l'intervalle [a, b], l'intégrale sera calculée comme la surface S mesurée sous la courbe, mais avec un signe négatif. En d'autres termes, on considère que c'est une surface négative. Dans le cas où la fonction f(x) présente des parties positives et des parties négatives sur l'intervalle, l'intégrale sera la somme des aires sous les parties positives et la soustraction des aires sous les parties négatives. Il est important de noter que l'intégrale est positive quand la fonction est au-dessus de l'axe horizontal, et négative quand elle est en dessous. N'hésitez pas à poser des questions supplémentaires.
Révisions Maths lycée
Analyse Terminale
ECG

Encadrement et intuition graphique
Dans cette vidéo, nous allons explorer différentes méthodes pour approximer l'aire sous une courbe. L'objectif est de mieux comprendre le calcul de cette aire. Lorsque la courbe est une droite, le calcul de l'aire est relativement simple, en utilisant des formes géométriques telles que des triangles ou des rectangles. Cependant, dès que la courbe devient incurvée, cela se complique. Nous allons donc examiner plusieurs méthodes d'approximation, dont la méthode des rectangles supérieurs et inférieurs, qui sont les plus couramment utilisées.
Avant de passer aux graphiques, examinons la définition officielle des rectangles supérieurs et inférieurs. Pour une fonction continue et positive f sur un intervalle AB, nous divisons cet intervalle en n petits intervalles de même amplitude, sur lesquels nous construisons des rectangles inférieurs et supérieurs. Les rectangles inférieurs sont situés juste en dessous de la courbe, tandis que les rectangles supérieurs sont situés juste au-dessus de la courbe. Lorsque le nombre de rectangles augmente et que leur finesse augmente également, les deux méthodes tendent vers la valeur réelle de l'aire sous la courbe.
Pour illustrer ces méthodes, regardons un graphique où la fonction est croissante. La méthode des rectangles inférieurs consiste à placer plusieurs rectangles sous la courbe. Plus le nombre de subdivisions augmente, plus les rectangles deviennent fins et se rapprochent de la courbe. Ainsi, les différences entre l'aire des rectangles et l'aire réelle sous la courbe deviennent de plus en plus petites.
La méthode des rectangles supérieurs consiste à placer des rectangles au-dessus de la courbe. Dans ce cas, l'aire des rectangles est légèrement supérieure à l'aire réelle sous la courbe, et est également supérieure à l'aire des rectangles inférieurs.
En dehors de ces deux méthodes courantes, nous avons également mentionné la méthode du point milieu et la méthode des trapèzes. La méthode du point milieu consiste à placer des rectangles traversés par la courbe au milieu de leur côté supérieur, permettant ainsi une approximation plus précise.
La méthode des trapèzes offre encore plus de liberté, car les quadrilatères utilisés ne sont plus des rectangles, mais des trapèzes. Cela permet de mieux coller à la courbe.
Cette vidéo vise à aider les personnes travaillant sur le calcul d'aires et d'intégrales à mieux visualiser ces concepts. Nous espérons que cela vous a été utile. Si vous avez des questions, n'hésitez pas à les poser dans la FAQ. À bientôt dans une prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
ECG

Intégrale et Aire
Dans ce cours, nous apprenons comment calculer une intégrale en utilisant une méthode géométrique basée sur le calcul d'erreurs. Cette méthode est applicable lorsque la forme géométrique de la fonction est simple, comme c'est le cas avec une fonction affine.
Nous nous intéressons ici à l'intégrale de la fonction x + 2, tracée sur le graphique entre -0,5 et 2. L'intégrale correspond à l'erreur sous la courbe par rapport à l'axe des abscisses. Deux méthodes sont possibles : calculer la primitive de x + 2 et effectuer le calcul habituel, ou reconnaître que la forme géométrique est un trapèze, dont nous pouvons facilement calculer l'erreur.
Pour calculer l'erreur, nous avons besoin de la hauteur, de la largeur et des longueurs des bases du trapèze. Pour cela, nous déterminons les coordonnées des points a, b, c et d. Les points a et b appartiennent à la droite définie par l'équation y = x + 2. Avec les abscisses x a = -0,5 et x b = 2, nous pouvons calculer les ordonnées correspondantes : y a = -0,5 + 2 = 1,5 et y b = 2 + 2 = 4. Les points c et d se situent sur l'axe des abscisses, donc leurs coordonnées sont respectivement (2, 0) et (-0,5, 0).
Ensuite, nous calculons les différentes longueurs en prenant la différence entre les ordonnées correspondantes. Ainsi, la longueur a, d est de 1,5, la longueur b, c est de 4 et la longueur d, c est de 2,5. En utilisant la formule de l'aire du trapèze, qui est la moyenne des deux bases multipliée par la hauteur, nous obtenons une valeur de 6,875 pour l'aire de ce trapèze.
Il est intéressant de remarquer que l'aire d'un trapèze peut être calculée en considérant soit la moyenne des deux côtés parallèles fois la base, soit la base fois la moyenne des hauteurs. Cette approche géométrique évite le calcul des primitives et permet de directement calculer l'aire géométrique de l'intégrale.
Ceci résume le cours sur le calcul d'une intégrale en utilisant une méthode géométrique basée sur l'aire.
Révisions Maths lycée
Analyse Terminale
ECG

Méthode des Rectangles
Dans ce cours, nous allons effectuer un calcul d'aire géométrique en utilisant la méthode des rectangles. La courbe intégrée n'a pas une forme géométrique simple, donc nous ne pouvons pas calculer directement l'aire géométriquement. Cependant, nous pouvons l'encadrer en utilisant la méthode des rectangles.
La courbe en rouge représente notre courbe et nous voulons trouver l'aire sous cette courbe. Nous pouvons dire que cette aire est plus grande que la somme des aires des petits rectangles situés en dessous de la courbe et plus petite que la somme des aires des grands rectangles situés au-dessus de la courbe. En diminuant la largeur des rectangles, nous affinons notre encadrement et lorsque la largeur tend vers zéro, les deux aires se rapprochent et tendent vers l'aire que nous cherchons, c'est-à-dire l'intégrale. Ce concept est appelé les intégrales de Riemann.
Dans cet exemple, nous cherchons à encadrer l'aire sous la courbe de 0 à 4. Comme la fonction f est croissante, nous pouvons l'encadrer en disant que l'aire sous la courbe est plus petite que a'0 + a'1 + a'2 + a'3, qui représente les grands rectangles, et plus grande que les aires a'1, a'2, a'3, qui représentent les petits rectangles.
Les aires des rectangles sont faciles à calculer en utilisant la formule largeur fois hauteur. Par exemple, a'1 a une largeur de 1 et une hauteur de f2, qui est la valeur de la fonction f pour x = 1. En utilisant la fonction f qui est la racine de x, nous pouvons calculer que a'1 = 1.
Nous continuons de calculer les aires des autres rectangles, et nous trouvons que a'2 = racine de 2 et a'3 = 2. Nous pouvons donc encadrer cette intégrale en disant que l'aire sous la courbe est plus petite que 3 + racine de 2 + racine de 3, et plus grande que 1 + racine de 2 + racine de 3.
Cet encadrement n'est pas très précis car nous avons une différence de 2 entre les valeurs maximales et minimales. Cependant, en augmentant la précision en utilisant des rectangles de largeur plus petite, nous pouvons obtenir un encadrement plus fin qui se rapproche davantage de la courbe.
En résumé, la méthode d'encadrement des rectangles permet d'approximer l'intégrale d'une fonction lorsque nous ne pouvons pas trouver une primitive de cette fonction. En diminuant la largeur des rectangles, nous affinons notre encadrement et nous approchons de l'aire réelle sous la courbe. Cette méthode est similaire à celle utilisée par les calculatrices pour calculer une aire en approximant par des petits carrés.


