 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Produit Scalaire
- Géométrie avec Repères
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Produit Scalaire
- Géométrie avec Repères
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Géométrie
Première
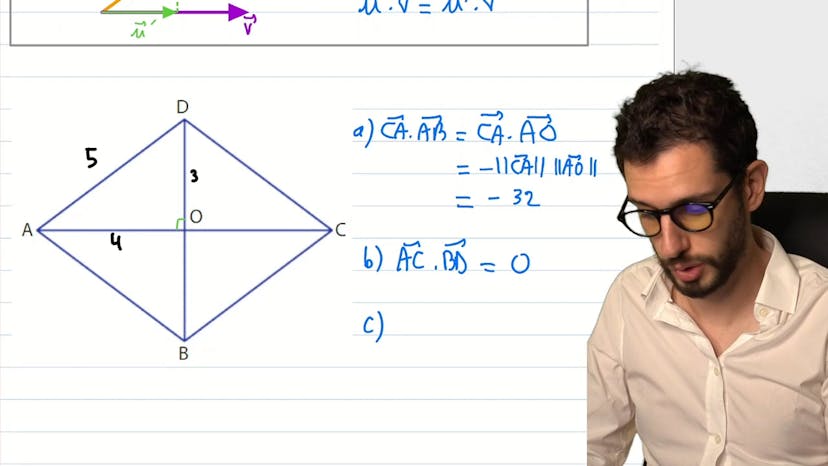
Définition de base : avec projeté
Le cours traite des propriétés fondamentales du produit scalaire. Le produit scalaire est défini comme le produit de deux vecteurs, qui est égal à la norme des vecteurs s'ils sont dans le même sens et moins le produit des deux normes s'ils sont dans des sens opposés. Si les vecteurs ne sont pas alignés, le produit scalaire sera égal à la version projetée du vecteur sur l'autre. Le cours utilise l'exemple d'un losange pour illustrer ces concepts et calcule plusieurs produits scalaires en utilisant la projection. Il rappelle également que le produit scalaire de deux vecteurs est nul s'ils sont orthogonaux. Enfin, le cours insiste sur l'utilité de la projection pour calculer des produits scalaires plus facilement.
Maths
Géométrie
Première
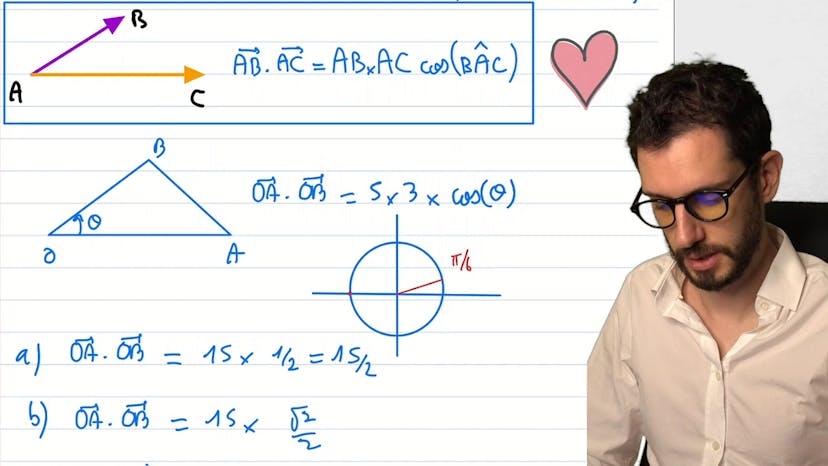
Définition avec le cosinus
La méthode enseignée est une manière d'utiliser la formule classique du produit scalaire AB scalaire AB qui est le produit des normes fois le cosinus de l'angle qui sépare les deux vecteurs. Pour l'appliquer, on prend l'exemple d'un triangle OAB avec OA=5 et OB=3, et on calcule le produit scalaire OA scalaire OB pour différentes valeurs de l'angle theta, soit pi sur 3, pi sur 4, et 5pi sur 6. Pour calculer le cosinus de theta, on utilise des rappels de trigonométrie. Pour le cas de 5pi sur 6, il est expliqué que le produit scalaire peut être négatif à cause de l'angle obtus du triangle. Cette méthode est présentée comme une manière d'illustrer le cours, plutôt qu'une résolution de problème.
Maths
Géométrie
Première

Définition avec des coordonnées
Cette méthode utilise deux formules de produits scalaires pour calculer un angle entre deux vecteurs dans un repère orthonormé. La formule pour trouver le produit scalaire est U scalaire V égal à la coordonnée de U multipliée par la coordonnée de V, soit le produit de leurs abscisses plus le produit de leurs ordonnées. Pour trouver l'angle NMP, on doit calculer les coordonnées de MN et MP, puis calculer leur produit scalaire. En utilisant la formule cosinus=NMP/∥ MN ∥∥ MP ∥, on peut trouver la valeur du cosinus de l'angle et l'approximer à 0,01° près. La méthode peut être utilisée pour résoudre des exercices de mathématiques de différents niveaux.
Maths
Géométrie
Première

Produit scalaire et perpendicularité
Le cours aborde la puissance du produit scalaire dans l'étude de la perpendicularité. Si le produit scalaire de deux vecteurs est nul, cela équivaut à l'orthogonalité de ces deux vecteurs. Cela permet de simplifier la vérification de la perpendicularité de deux droites en calculant leur produit scalaire. La méthode consiste à déterminer les vecteurs des droites PQ et RS, puis à calculer leur produit scalaire pour vérifier leur orthogonalité. Cela peut être utile en physique ou en maths pour montrer la perpendicularité, même dans l'espace.
Maths
Géométrie
Première

Formule d'Al-Kashi
Le théorème d'Alkaci est une formule importante dans le chapitre du produit scalaire. Il permet de trouver la valeur exacte et unique du troisième côté d'un triangle lorsque l'on connaît les longueurs de deux côtés et l'angle entre eux. C'est une généralisation du théorème de Pythagore dans le cas d'un triangle qui n'est pas rectangle. La formule d'Alkaci est une version corrigée du théorème de Pythagore, qui inclut un terme correctif lié au produit scalaire. Lorsque l'angle entre les deux côtés est de 90 degrés, la formule d'Alkaci se réduit à celle de Pythagore. On peut donc l'utiliser pour vérifier si un triangle est rectangle. Dans un exercice, on applique la formule d'Alkaci pour trouver la longueur d'un côté d'un triangle connaissant les longueurs des deux autres côtés et l'angle entre eux. Après avoir effectué les calculs, on trouve une valeur pour le côté manquant. En résumé, le théorème d'Alkaci permet de trouver la valeur exacte d'un côté de triangle en utilisant les longueurs de deux côtés et l'angle entre eux.
Maths
Géométrie
Première
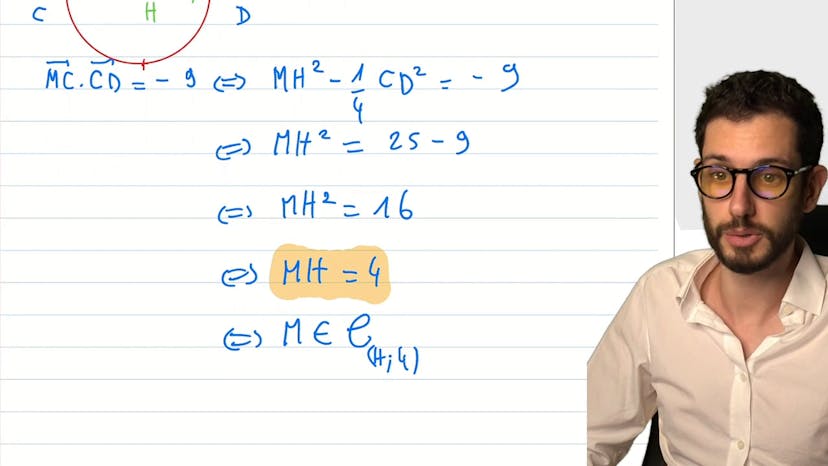
Ensembles de points à reconnaître
Ce cours traite des produits scalaires et d'une formule très pratique qui permet de déterminer un ensemble de points vérifiant un produit scalaire égal à une valeur donnée. Cette formule s'applique lorsque l'on a deux points A et B qui forment un segment et qu'on appelle I son milieu. Pour un point M quelconque, la formule nous permet d'exprimer le produit scalaire MA.MB en fonction de M, par exemple MI carré moins un quart de AB carré. Cette formule peut être très utile pour résoudre certains problèmes de géométrie. Lorsque l'on cherche des points M vérifiant un produit scalaire égal à une valeur donnée, il faut appliquer cette formule en posant le milieu H si celui-ci n'a pas été donné. Ensuite, si on nous demande de trouver les points tels que MH égal 4, il s'agit de reconnaître l'ensemble des points à une distance constante de H, soit un cercle de centre H et de rayon 4.
Maths
Géométrie
Première
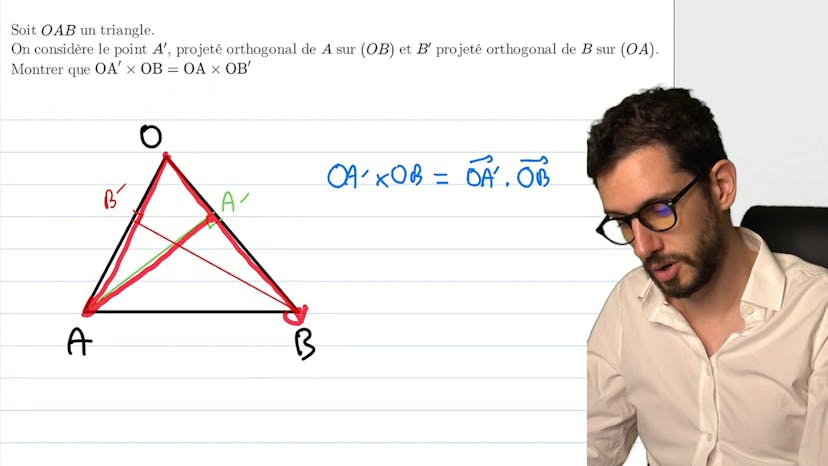
Produit scalaire : 0 calculs, que des projections
Dans cet exercice, on observe un triangle OAB et on cherche à démontrer que OA' x OB est égal à OA x OB'. On commence par trouver les points A' et B', qui sont les projections orthogonales de A et B sur les côtés opposés. Ensuite, on utilise la propriété du produit scalaire pour exprimer OA' x OB en fonction d'un produit scalaire, et on remarque que ce produit scalaire est également égal à OA' x OB'. Ce faisant, on peut exprimer OA' x OB' en fonction d'un produit scalaire, ce qui nous permet de prouver que OA' x OB est bien égal à OA x OB'. Cet exercice montre l'utilité du produit scalaire dans la résolution de problèmes de géométrie.
Maths
Géométrie
Première

Produit scalaire dans un carré
L'exercice consiste à calculer des produits scalaires à partir de projections. On utilise la propriété selon laquelle le produit scalaire entre deux vecteurs est égal à leur projection sur une même direction. On démontre ainsi que AB scalaire AC est égal à AB au carré, que AB scalaire AD est égal à zéro, que OC.OD est égal à zéro, que AC.AO est égal à la moitié de A², que OC.OA est égal à moins un demi A² et que AD.OB est égal à moins un demi A² également. L'exercice permet de se familiariser avec la formule des projections, qui permet de simplifier les calculs.
Maths
Géométrie
Première

Chasles pour trouver un ensemble de points
Cet exercice consiste à trouver l'ensemble des points M du plan vérifiant MA ⋅ MB + MC = 0, sachant que a' est le milieu du segment abaissé. Pour simplifier l'expression, il faut trouver un moyen d'avoir du M concentré en un seul endroit. En utilisant la formule du milieu, on peut remplacer MB par MA' + A'B et MC par MA' + A'C, et ainsi dégager A'B et A'C. Il reste alors MA ⋅ 2MA', soit MA ⋅ MA', qui correspond à l'ensemble de points connus dans le cours, à savoir le cercle de diamètre AB. En effet, tout point M vérifiant MA ⋅ MB = 0 est perpendiculaire à MB, ce qui correspond à un point sur le cercle de diamètre AB. On peut donc conclure que l'ensemble des points M est l'ensemble des points du cercle de diamètre AA'.
Maths
Géométrie
Première

Au choix : avec ou sans coordonnées ?
Dans ce cours, on apprend à résoudre un problème de géométrie avec des produits scalaires de deux manières : avec un système de coordonnées ou en utilisant la géométrie pure. La résolution avec coordonnées est très simple : on donne les coordonnées de tous les points et on calcule les coordonnées des vecteurs DE et AF pour démontrer que DE et AF sont perpendiculaires en appliquant la formule du produit scalaire. En revanche, la résolution sans coordonnées est un peu plus complexe : il faut réfléchir à comment décomposer DE et AF. En fin de compte, il faut développer le produit scalaire de DA plus AE et AB plus BF pour arriver à la conclusion que DE est orthogonal à AF. Même si la résolution sans coordonnées peut être plus créative, elle est souvent moins intuitive que la résolution avec coordonnées.
Maths
Géométrie
Première

Caractériser un rectangle
In this video transcription, the goal is to prove that BA dot BC equals one quarter of (BD squared minus AC squared), where BCD is a parallelogram with a center at point H. The speaker initially tries to approach the problem from both sides but finds that it doesn't work well. Instead, they recommend starting from the left side and trying to simplify as much as possible, then doing the same for the right side, and finally comparing the two to see if they can be shown to be equal. The speaker also notes that the fact that H is the center of the parallelogram is important and should be used. By treating BD squared minus AC squared as a scalar function of AC, the speaker is able to simplify the expression to 4 times BO squared minus AO squared, which can then be compared to BO squared minus AO squared plus OC squared minus OA squared. Finally, it is shown that if BA dot BC equals 0, then BD equals AC, proving that ABCD is a rectangle. The main takeaway from this video is the method of approaching a problem from both sides and simplifying as much as possible before comparing the two expressions.
Maths
Géométrie
Première
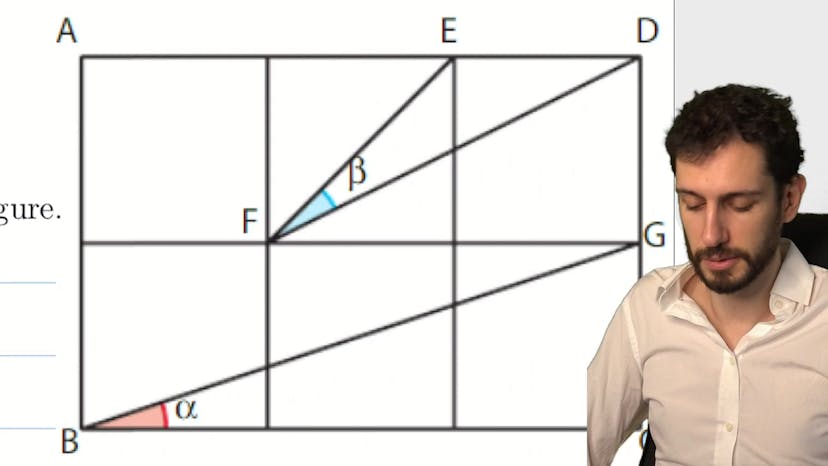
Comparer des angles : quelle formule appliquer ?
Dans cet exercice, il faut comparer les valeurs des angles alpha et beta d'une figure composée de 6 carrés de côté 1. Pour trouver les valeurs des angles, on peut utiliser le théorème d'Al-Kashi qui permet de calculer la mesure d'un côté en fonction des deux autres côtés et de l'angle correspondant. Pour alpha, on peut facilement accéder au cosinus en utilisant un triangle rectangle. Pour beta, on doit utiliser un triangle quelconque et appliquer Al-Kashi pour calculer la valeur de cos beta. Ensuite, il suffit de comparer les valeurs de cos alpha et cos beta pour déterminer lequel des deux angles est plus grand. On peut remarquer que les deux angles sont entre 0 et pi sur 2, ce qui permet de dire que si alpha est plus grand que beta, alors cos alpha est plus petit que cos beta. En résolvant l'exercice, on trouve que cos alpha et cos beta sont égaux, donc alpha = beta. L'exercice permet de tester notre utilisation du théorème d'Al-Kashi et notre réflexe pour résoudre des problèmes avec des angles bizarres.


