Online Primitives & Équations Différentielles course by Top Instructors - Primitives & Équations Différentielles

Introduction Primitives

Le chapitre des primitives est basé sur la notion d'antidérivation, qui consiste à trouver une fonction telle que sa dérivée soit la fonction à dériver. On appelle cette fonction la primitive. Pour trouver celle-ci, on utilise un tableau de dérivation avec quelques nuances à connaître. Les applications des primitives sont présentes en physique, chimie, économie, etc. Pour réussir ce chapitre, il faut connaître la définition, savoir déterminer l'ensemble des primitives d'une fonction, transformer l'écriture d'une fonction pour obtenir les bonnes primitives et enfin, savoir déterminer les primitives des fonctions composées.

Primitive : Définition

Une primitive d'une fonction f définie sur un intervalle i réel est une fonction F qui est solution de l'équation différentielle y' = f. Une fonction F est primitive de f lorsque pour toute x de l'intervalle de définition, F'(x) = f(x). Il existe un tableau de primitives qu'il faut connaître par cœur pour répondre aux questions sur les primitives. Souvenez-vous également que la dérivée d'une constante est nulle, donc quand vous décrivez l'ensemble des primitifs possibles, n'oubliez pas d'ajouter une constante. Il y a une infinité de fonctions qui ont la même valeur dérivée, toutes celles qui sont la même mais translatées vers le haut ou vers le bas. Les fonctions xⁿ deviennent xⁿ⁺¹ / n⁺¹, toujours plus k, et il y a d'autres fonctions à connaître.

Existence et Calcul des Primitives

Ce cours explique les théorèmes importants sur les primitives. Le premier théorème stipule que toute fonction continue sur un intervalle a des primitives sur l'intervalle. Le deuxième théorème indique que pour tout réel de l'ensemble des définitions de base, s'il y a une valeur y0, il y a une primitive unique parmi toutes les primitives qui passe exactement par ce point. Le troisième théorème expose que l'ensemble de toutes les primitives équivaut à l'ensemble des F plus K. Ces théorèmes sont essentiels pour comprendre les primitives.

Primitives : condition initiale

Dans cet exercice, il s'agit de vérifier qu'une fonction composée est bien une primitive d'une fonction donnée, puis d'en déduire l'ensemble des primitives de cette fonction. Pour cela, on regarde l'ensemble de définition de dérivabilité, et on dérive la fonction composée pour vérifier qu'elle retombe bien sur la fonction donnée. On précise qu'il y a une infinité de primitives possibles définies à une constante additive près. Ensuite, on cherche à déterminer l'unique primitive qui prend une valeur fixe donnée, appelée condition initiale. L'ensemble des primitives de cette fonction est de la forme F(x) + ln(x) + K où K est une constante réelle, et la primitive qui s'annule à une valeur donnée est de la forme F(x) + ln(x) - 1 - E³. Cet exercice introduit les méthodes sur les primitives, utiles notamment pour la résolution des équations différentielles.

Transformer puis primitiver

Apprenez comment trouver une primitive à partir d'une fonction sur laquelle a priori on ne la trouve pas. Pour cela, vous pouvez utiliser la méthode d'identification sous la forme u prime fois u, ou la décomposition en éléments simples si vous avez une fonction rationnelle. Par exemple, pour la fonction f de x qui a la 3x² plus 2 facteur de x au cube plus 2x, vous pouvez trouver la primitive en identifiant u prime qui est égal à 3x² plus 2, et vous obtenez 1 demi de x au cube plus 2x au carré plus une constante. Pour la fonction rationnelle g qui est aussi sous forme d'un produit au dénominateur, vous pouvez utiliser la décomposition en éléments simples en trouvant les réels a et b tels que g de x soit égal à a sur x plus b sur x-1. Dans ce cas, vous pouvez calculer la primitive de chacune d'entre elles, et identifier facilement la primitive de g qui est ln de x moins 1 plus moins ln de x. Gardez à l'esprit que selon l'intervalle de définition, une fonction peut avoir des primitives qui ont une expression différente, comme dans le cas de la fonction 1 sur x qui a des primitives différentes sur r étoile moins et sur r étoile plus.

Composition et Primitives

Dans ce cours, nous apprenons à repérer des formes de fonctions composées afin de trouver plus facilement leurs primitives. Certaines formes comme U' sur racine de U, cos U fois U', U' x sin U, U' x E2U et U' sur U^n reviennent souvent et sont faciles à primitiver. L'opération inverse implique également la connaissance des dérivées des mêmes formes. La constante multiplicative n'est pas un problème et peut être trouvée en effectuant une bête décomposition. En prenant un exemple de fonction exponentielle U', nous avons vu comment trouver ses primitives en ajoutant le coefficient manquant et en utilisant la constante multiplicative. Toutes les primitives sont de la forme 1/6e de e^3x²-5 plus une constante, et sont fonctions de la forme de la fonction découvertes.

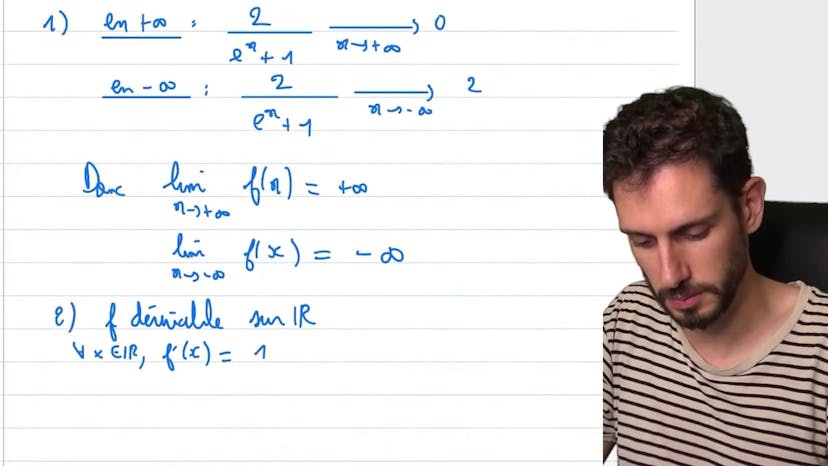
Primitive et réécriture

Ce cours concerne l'analyse d'une fonction définie par f2x = x + log(4) + 2/(e2x + 1). L'objectif est de trouver une expression de primitive facile à détecter. Tout d'abord, on étudie les limites de la fonction. La limite lorsque x tend vers plus l'infini est x, car le reste de l'expression tend vers 0. La limite lorsque x tend vers moins l'infini est 2, car e2x tend vers 0 puisque x tend vers moins l'infini. Ensuite, on examine le sens de variation de la fonction. Comme f est dérivable sur R et que la dérivée est toujours positive, cela signifie que la fonction est croissante. Enfin, on trouve les primitives de la fonction. La primitive de x est x²/2. La primitive de 2 + log(4) est (2 + log(4))x. En utilisant une intégration par substitution, on obtient la primitive de -2e2x/(e2x+1) comme étant -log(e2x+1). Donc, l'ensemble des primitives possibles est x²/2 + (2 + log(4))x - log(e2x+1) + K, où K est une constante réelle. En résumé, on cherche une primitive de la fonction f2x = x + log(4) + 2/(e2x + 1). On étudie les limites, le sens de variation et les primitives de la fonction, et on obtient l'ensemble des primitives possibles.

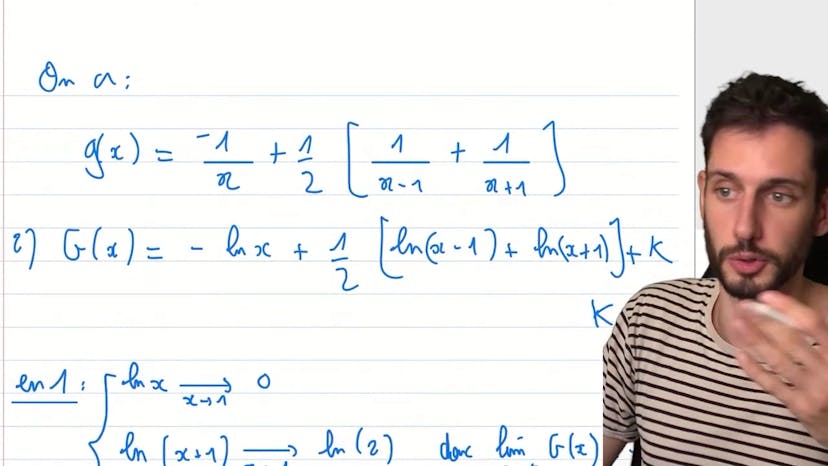
Décomposition en éléments simples

Ce cours concerne la simplification de fractions rationnelles contenant des polynômes. Il existe deux méthodes pour résoudre ces fractions, dont la méthode la plus simple consiste à mettre toutes les fractions au même dénominateur et à identifier les termes en fonction du degré du polynôme. Cependant, une méthode plus astucieuse consiste à utiliser les expressions x, x+1 et x-1 pour isoler les constantes a, b et c. Ensuite, il est possible de déterminer l'ensemble des primitives de g (la fraction rationnelle simplifiée), avec une constante k, et de trouver la limite de g en l'infini et en 1. En utilisant les propriétés des logarithmes, on peut simplifier l'expression de g et déduire que sa limite en l'infini est 0, quel que soit k.

Polynôme × exponentielle

En résumé, dans ce cours, on examine une fonction f(x) qui est un polynôme multiplié par une fonction exponentielle. On apprend que la primitive de cette fonction sera probablement un polynôme du même degré multiplié par l'exponentielle. On résout également quelques équations pour trouver les paramètres du polynôme. Finalement, on obtient l'expression de la dérivée de F(x).

Introduction Primitives

Dans ce cours, nous revenons sur la notion de dérivée avant d'aborder les primitives. La dérivée permet d'accéder à la pente des tangentes d'une courbe, ce qui permet de déterminer si la courbe monte ou descend. Cependant, la dérivation ne sert pas seulement à cela, elle permet également de déterminer quand une fonction est croissante, décroissante, ou s'il y a un maximum ou un minimum. La primitive est une notion inverse de la dérivée. Elle consiste à trouver une fonction F telle que sa dérivée soit égale à une fonction donnée f. C'est un peu comme une anti-dérivation. Il existe des formules pour les primitives, similaires à celles utilisées pour les dérivées. En connaissant ces formules, il est possible de trouver les primitives des fonctions. Par exemple, si la fonction donnée est 2x, sa primitive est x2/2. Il est important de noter que les tableaux de dérivation que nous avons appris précédemment peuvent être utilisés à l'envers pour trouver les primitives. Les applications des primitives sont nombreuses, notamment en physique, en chimie et en économie. Par exemple, en physique, les primitives sont utilisées pour retrouver le mouvement d'un objet à partir de ses accélérations. En chimie, elles sont utilisées pour étudier la vitesse de réaction d'un système. En économie, elles peuvent être utilisées pour optimiser les décisions d'investissement. Dans le cours sur les primitives, nous aborderons différents points tels que la définition des primitives, leur linéarité, leur existence selon certaines conditions, les primitives des fonctions composées, etc. Il sera également nécessaire d'apprendre les tableaux de primitives et de s'exercer à trouver les bonnes primitives. Si vous avez des questions supplémentaires, n'hésitez pas à les poser et consultez la FAQ pour plus de détails.

Primitive : Définition

Une primitive de la fonction f est une fonction qui satisfait l'équation différentielle y'=f. En d'autres termes, c'est une fonction F telle que F'=f. Une équation différentielle est une équation où l'inconnue est une fonction. Par exemple, l'exponentielle est une fonction qui vérifie l'équation y'=y. Les primitives d'une fonction peuvent être trouvées en utilisant le tableau de primitives, qui est l'inverse du tableau de dérivées. Il est important de noter qu'il faut toujours ajouter une constante lors de la recherche des primitives, car la dérivée d'une constante est nulle. Certaines fonctions peuvent avoir des primitives similaires. Par exemple, les fonctions 3x+2 et 3x+4 ont la même dérivée. Une illustration des primitives de la fonction f(x)=x² est donnée, montrant les différentes fonctions qui ont la même dérivée que x². Enfin, le tableau de primitives est présenté, donnant les expressions générales des primitives pour différentes fonctions. Il est conseillé de connaître ces expressions par cœur.

Existence et Calcul des Primitives

Ce cours aborde quelques théorèmes importants sur l'existence des primitives en mathématiques. Le premier théorème stipule qu'une fonction continue sur un intervalle a des primitives sur cet intervalle. Par exemple, la fonction constante 3 a plusieurs primitives, telles que 3x+2, 3x+5 et 3x-pi. On peut en trouver une infinité en ajoutant une constante. Le deuxième théorème indique que l'ensemble de toutes les primitives d'une fonction continue sur un intervalle est l'ensemble des fonctions de la forme F(x)+k, où F est une primitive de la fonction et k est une constante. Cela signifie qu'il n'y a pas d'autres formes de primitives possibles. Le troisième théorème affirme que pour tout réel y0, il existe une unique primitive qui passe exactement par ce point. Par exemple, si on fixe l'ordonnée 5, il n'y a qu'une seule primitive qui passe par ce point. La démonstration du premier théorème utilise une démonstration par condition nécessaire et suffisante. On montre que toute fonction qui est une primitive d'une autre fonction doit être de la forme F(x)+k. On prouve également que toute fonction de cette forme est une primitive. Enfin, le cours présente un tableau récapitulatif des différentes règles pour primitives, similaire au tableau des dérivées. Par exemple, la primitive de la somme de deux fonctions est la somme des primitives des fonctions, et la primitive d'une constante multipliée par une fonction est égale à cette constante multipliée par la primitive de la fonction. Il est important de maîtriser ces théorèmes et règles pour pouvoir calculer les primitives de fonctions de manière efficace.

Primitives : condition initiale

Dans cet exercice, nous devons vérifier si la fonction proposée, F(x) = x³ + ln(x), est bien une primitive de la fonction f(x) = 3x² + 1/x. Pour cela, nous allons dériver F(x) pour voir si nous obtenons f(x). En dérivant F(x), nous obtenons 3x² + 1/x, ce qui est bien égal à f(x). Donc F(x) est une primitive de f(x). Cependant, il est important de noter qu'il existe une infinité de primitives de f(x) qui diffèrent par une constante additive. Ainsi, l'ensemble des primitives de f(x) est de la forme F(x) + K, où K est une constante réelle. Ensuite, nous devons déterminer l'unique primitive de f(x) qui s'annule en un certain point E. Pour cela, nous évaluons F(E) + K et cherchons la valeur de K qui rend cette expression égale à zéro. En calculant F(E), nous obtenons E³ + 1 + K. En résolvant l'équation E³ + 1 + K = 0, nous trouvons que K = -1 - E³. Ainsi, la primitive de f(x) qui s'annule en E est F(x) + K = ln(x) + x³ - 1 - E³. Cet exercice introduit la notion de primitives et montre leur utilité pour la résolution des équations différentielles. N'hésitez pas à poser vos questions dans la FAQ si besoin.

Transformer puis primitiver

Dans ce cours, nous étudions comment trouver une primitive à partir d'une fonction pour laquelle il n'est pas évident de la trouver. Nous avons vu qu'il est généralement facile de dériver, mais trouver une primitive peut être compliqué. Nous avons pris comme exemple une fonction f(x) égale à 3x^2 + 2x^3 + 2x. Nous avons essayé de l'identifier sous la forme u' * u. Nous avons remarqué que le polynôme de degré 2 correspondait à u(x), et après avoir dérivé, nous avons obtenu que u' était égal à 3x^2 + 2, ce qui correspondait exactement à ce que nous avions au départ. Donc, finalement, nous avons trouvé que la primitive de u' * u était égale à 1/2u^2(x). De là, nous avons pu déterminer une primitive de f(x), qui était donc égale à 1/2(x^3 + 2x)^2. Ensuite, nous avons voulu trouver la primitive qui valait 5 lorsque x était égal à 1. Nous savions que toutes les primitives étaient de la forme f(x) + k, avec k appartenant à R, mais il y avait une seule primitive qui prenait la valeur 5 en x = 1. En résolvant l'équation, nous avons trouvé que k était égal à 1/2. Donc, finalement, la fonction cherchée était 1/2(x^3 + 2x)^2 + 1/2. Ensuite, nous avons considéré une nouvelle fonction g qui était aussi un produit, mais cette fois-ci au dénominateur. Nous avons utilisé une méthode classique pour les fonctions rationnelles, appelée décomposition en éléments simples. Nous avons trouvé que g(x) était égal à -1/(x+1) + 1/(x-1). En trouvant les primitives de chaque terme, nous avons obtenu que la primitive de g(x) était -ln(x) + ln(x-1). Après avoir vérifié que la dérivée était correcte, nous avons noté que cette fonction était définie pour x > 1, car g(x) était non définie pour x = 0 et x = 1. De plus, nous avons mentionné qu'une primitive de 1/x était ln(|x|), et qu'il fallait faire attention aux valeurs absolues lorsque la fonction était définie sur plusieurs intervalles. En conclusion, nous avons expliqué deux méthodes pour trouver des primitives : l'identification d'un produit sous la forme u' * u et la décomposition en éléments simples pour les fonctions rationnelles.

Composition et Primitives

Dans ce cours, nous apprenons à repérer des primitifs de fonctions composées. Certaines formes reviennent souvent et il est important de les reconnaître. Par exemple, lorsque nous avons U' sur la racine de U, la primitive sera deux racines de U. Si nous avons cos U fois quelque chose, et que c'est U' devant, la primitive est sin U. De la même manière, si nous avons U' fois sin U, la primitive est moins cos U. Lorsqu'il y a une exponentielle, la primitive est E2U. Si nous avons un coefficient U' sur U, la primitive est ln U. Lorsque nous avons U' fois U puissance n, la primitive est U puissance n plus 1 sur n plus 1. Pour vérifier si notre proposition de primitive est correcte, nous pouvons dériver et voir si nous obtenons la bonne fonction. Si nous avons U' sur U puissance n, la primitive est moins 1 sur n-1 fois 1 sur U puissance n-1. Il est également important de connaître les dérivées des primitifs inverses, comme U' de racine de U. Nous pouvons également utiliser des constantes multiplicatives lorsque cela est nécessaire pour trouver la bonne valeur de notre primitive. En pratique, pour trouver les primitives d'une fonction donnée, nous devons repérer la forme de base et ajuster si nécessaire. Par exemple, si nous avons une exponentielle de U, nous pouvons introduire un coefficient multiplicatif à l'intérieur de la fonction pour correspondre à la dérivée. Ensuite, nous pouvons déterminer la forme générale des primitives, en ajoutant une constante. En conclusion, il est important de reconnaître les formes courantes des primitifs de fonctions composées et de savoir comment ajuster si nécessaire.

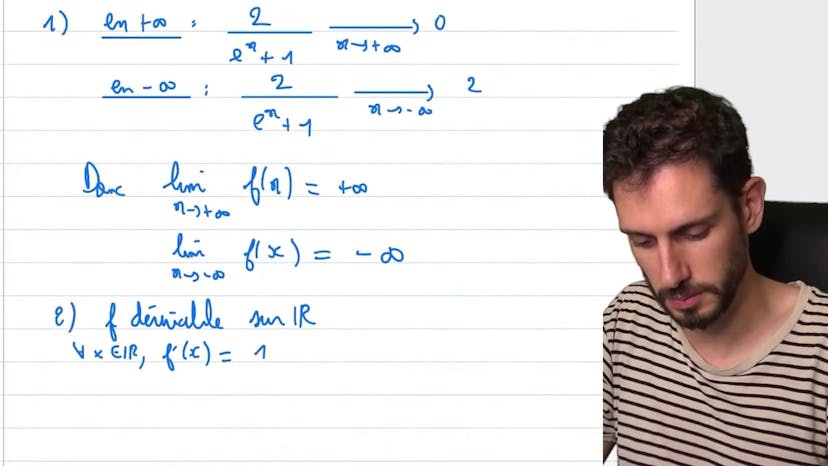
Primitive et réécriture

Ce cours porte sur l'analyse d'une fonction f(x) = x + log(4) + 2/(e^(2x) + 1). Dans la première partie de l'exercice, on cherche à analyser cette fonction pour trouver une expression de sa primitive qui soit facile à détecter. Pour commencer, on calcule la limite de f(x) lorsque x tend vers plus l'infini et moins l'infini. On constate que la limite est de 0 lorsque x tend vers plus l'infini et de 2 lorsque x tend vers moins l'infini. Ensuite, on étudie le sens de variation de f et on dresse le tableau des variations. On observe que f est dérivable sur R et que sa dérivée est toujours positive. Donc, f est croissante sur tout R. Pour trouver les primitives de f(x), on remarque que la fonction peut être réécrite comme x + log(4) + 2 - 2/(e^(2x) + 1). On calcule cette expression et on obtient x^2/2 + 2x + log(e^(2x) + 1) + K, où K est une constante. Donc l'ensemble des primitives de f(x) est donné par x^2/2 + 2x + log(e^(2x) + 1) + K, avec K appartenant à R.

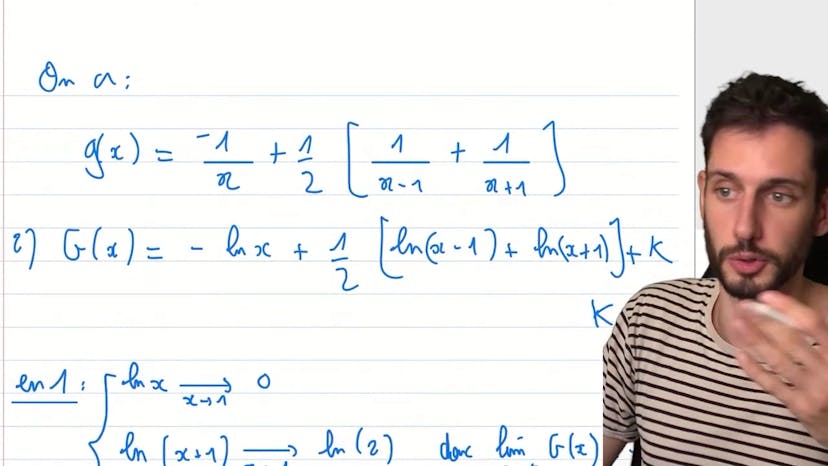
Décomposition en éléments simples

Dans ce cours, nous apprenons à simplifier les fractions rationnelles en séparant les monômes, c'est-à-dire les polynômes du degré 1. Il existe deux méthodes pour y parvenir : la première consiste à mettre tous les termes au même dénominateur et à résoudre un système d'équations, tandis que la seconde méthode est plus rapide. La deuxième méthode consiste à prendre en compte trois pôles (x, x+1, x-1) et à utiliser cette expression pour isoler les constantes a, b et c. Ensuite, nous déterminons les primitives de cette fonction et ajoutons une constante k. Enfin, nous déterminons les limites en l'infini et en 1 de ces primitives. Pour cela, nous utilisons les propriétés du logarithme. Au final, nous obtenons une fonction qui tend vers 0 lorsque x tend vers l'infini, et nous pouvons simplifier cette fonction en utilisant les propriétés du logarithme.