 All subjects
All subjects
 All subjects
All subjects
Maths Spé
Analyse
Terminale

Calcul Valeur Moyenne
La valeur moyenne d'une fonction f sur un intervalle est donnée par l'intégrale de la fonction sur l'intervalle, divisée par la largeur de l'intervalle. On peut déterminer la primitive de la fonction f en utilisant le théorème fondamental de l'intégration. Une fois la primitive trouvée, on peut calculer la valeur moyenne en substituant les bornes de l'intervalle dans la primitive et en effectuant les calculs nécessaires.
Dans l'exemple présenté, nous avons deux fonctions f et g avec des intervalles légèrement différents. Pour calculer la valeur moyenne de f, nous posons h(x) = x² + 3 et utilisons le théorème fondamental pour trouver une primitive de h, qui est H(x) = (1/3)x³ + 3x. En utilisant la définition de la valeur moyenne, nous divisons l'intégrale de f sur l'intervalle par la largeur de l'intervalle pour obtenir la valeur moyenne 13/3.
Pour calculer la valeur moyenne de g, nous avons la fonction g(x) = x / (x² - 3) et la largeur de l'intervalle est 4 - e. En cherchant une primitive de g, nous remarquons qu'elle ressemble à un quotient de dérivées. Nous ajustons légèrement le quotient pour obtenir la forme u' / u, avec u = x² - 3. La primitive de g est alors k(x) = (1/2)ln|x² - 3|. En simplifiant l'expression et en substituant les bornes de l'intervalle, nous obtenons la valeur moyenne de g.
Il suffit d'appliquer la définition de la valeur moyenne et de faire les calculs d'intégration pour obtenir la valeur moyenne d'une fonction sur un intervalle donné.
Maths Spé
Analyse
Terminale

Suite d'Intégrales
Dans ce cours, on étudie une suite d'intégrales et on cherche à trouver sa convergence. On nous pose une suite de fonctions fn de t qui vaut 1 sur 1 plus t à la puissance n et in qui va être l'intégrale de 0 à 1 de cette fonction fn. On guide l'exercice en essayant d'encadrer cette fonction entre 1 et 1 moins t à la puissance n. La première méthode consiste à construire des inégalités. On obtient le premier bout de l'inégalité en suivant ce raisonnement : 1,5 est compris entre 1 sur 1 plus t à la puissance n qui est plus petit que 1. Pour le deuxième, on multiplie par moins 1 et on essaie de sommer avec l'autre inégalité. Quand cela ne marche pas, on fait la méthode instinctive en faisant la différence.Ensuite, on calcule l'intégrale en utilisant la linéarité de l'intégrale et on trouve l'encadrement de la suite.Finalement, on utilise le théorème d'encadrement pour montrer que la suite converge et donner sa limite qui est 1.
Maths Spé
Analyse
Terminale
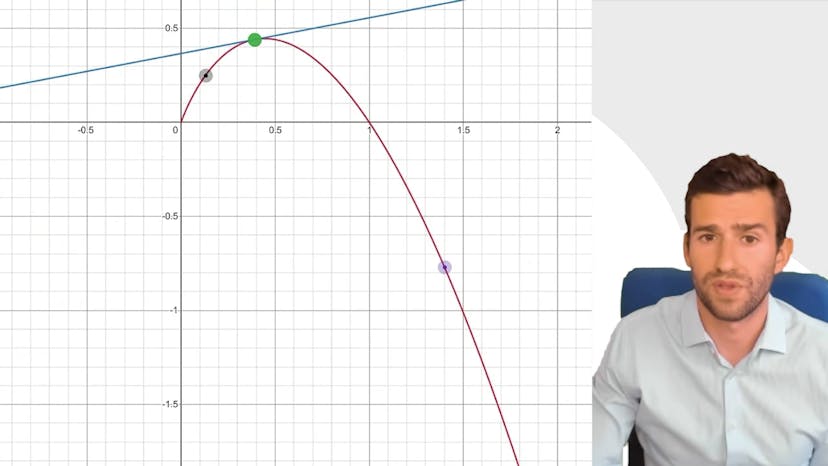
Convexité et f''
La convexité d'une fonction est un concept important en mathématiques. Pour déterminer si une fonction f(x) est concave ou convexe, il suffit d'observer le signe de la dérivée seconde de la fonction.
Dans le premier exemple, la fonction f(x) = (1/3)x^3 - (3/2)x^2 + 2x + 1 est un polynôme dérivable deux fois. En dérivant deux fois la fonction, on obtient f''(x) = 2x - 3. On remarque que f''(x) est positif pour x > 3/2 et négatif pour x < 3/2. Par conséquent, la fonction f(x) est concave lorsque x < 3/2 et convexe lorsque x > 3/2.
Dans le deuxième exemple, la fonction f(x) = 3x - 3x^(3/2) est définie sur l'ensemble des réels positifs (r*+). En dérivant et en calculant la dérivée seconde, on obtient f''(x) = -9/(4√x). Comme racine de x est toujours positive, on en déduit que f''(x) est toujours négatif. Ainsi, la fonction f(x) est concave sur tout son ensemble de définition.
La concavité d'une fonction peut être interprétée en termes de tangentes. Lorsqu'une fonction est concave, la tangente est située au-dessus de la courbe sur tout l'intervalle où la fonction est concave. On dit alors que la tangente est sécante avec la courbe en un unique point, le point de tangence. De plus, la courbe est toujours au-dessus des cordes définies par deux points de la courbe.
En conclusion, l'étude de la concavité et de la convexité d'une fonction permet de déterminer la position relative de la tangente par rapport à la courbe. Une fonction concave est en dessous de sa tangente, tandis qu'une fonction convexe présente la situation inverse.
Maths Spé
Analyse
Terminale
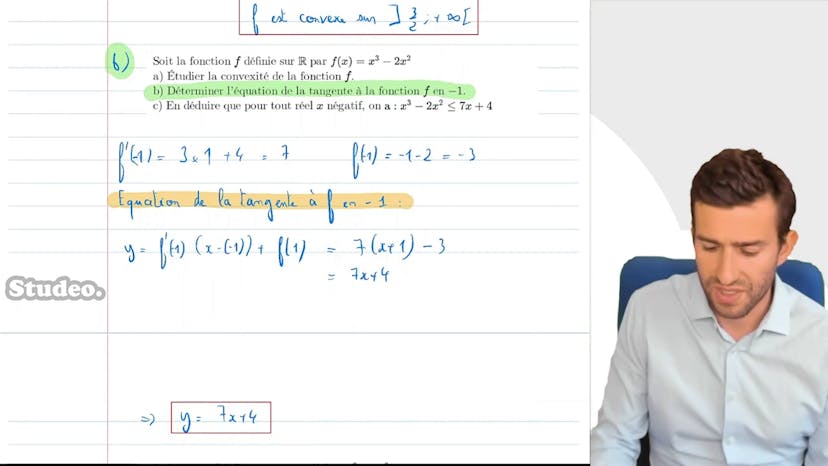
Convexité et Inégalités
Dans ce cours, nous étudions la méthode de la convexité en SEO friendly. La méthode est assez classique et facile à appliquer une fois que l'on maîtrise l'étude de la convexité. Nous commençons par nous intéresser à une fonction f(x) égale à x^3 - 2x^2, qui est un polynôme dérivable deux fois. Nous calculons les deux dérivées de cette fonction : f'(x) = 3x^2 - 4x et f''(x) = 6x - 4.
Nous souhaitons étudier le signe de f''(x) pour déterminer la concavité et la convexité de la fonction. En résolvant l'inéquation 6x - 4 > 0, nous trouvons que x > 3/2. En résolvant l'inéquation 6x - 4 < 0, nous trouvons que x < 3/2. Nous en déduisons que la fonction f est concave sur l'intervalle ]-∞, 3/2] et convexe sur l'intervalle [3/2, +∞].
Ensuite, on nous demande l'équation de la tangente de f au point -1. En utilisant la formule y = f'(1)(x - (-1)) + f(1), nous trouvons que l'équation de la tangente est y = 7x + 4.
Nous devons ensuite déduire que pour tout x négatif, x^3 - 2x^2 < 7x + 4. En analysant cette inégalité, nous observons que 7x + 4 est l'équation de la tangente que nous avons calculée précédemment, et x^3 - 2x^2 est la fonction f. Ainsi, géométriquement, cette inégalité signifie que la courbe représentant la fonction f est située en dessous de sa tangente. Cela est vrai lorsque la fonction est concave, ce qui est le cas sur l'intervalle ]-∞, 3/2]. Par conséquent, nous avons bien l'inégalité souhaitée.
Il est important de noter que cette méthode repose sur l'analyse de la convexité de la fonction. Sans cette notion, on ne pourrait pas résoudre l'équation x^3 - 2x^2 < 7x + 4, car elle implique un polynôme de degré 3. Il faut donc toujours penser à la convexité pour résoudre ce type d'équations.
En conclusion, la méthode de la convexité nous permet d'étudier la concavité et la convexité d'une fonction, de trouver l'équation de la tangente en un point et d'établir des inégalités entre une fonction et sa tangente. N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires.
Maths Spé
Analyse
Terminale

Points d'Inflexion
Ce cours porte sur la convexité des fonctions et les points d'inflexion. La fonction étudiée est f2x et nous allons la dériver deux fois pour trouver ses variations.
Nous commençons par calculer la première dérivée, f', qui est toujours positive car l'exponentielle dans la fonction est positive. Le signe important est celui de "-x plus 1". Ce terme est positif pour x allant de moins l'infini à 1 et négatif sinon. Nous en déduisons que la dérivée est positive pour x < 1 et négative pour x > 1.
En utilisant ces informations, nous construisons le tableau de variations de la fonction f. Elle est croissante jusqu'à x = 1, puis décroissante. Son maximum est atteint à x = 1, avec une valeur de 7e-1.
Nous calculons également les limites de la fonction aux infinis. Pour x tendant vers moins l'infini, la limite est moins l'infini, tandis que pour x tendant vers plus l'infini, la limite est 0. Nous avons ainsi un tableau de variations complet.
Ensuite, nous calculons la seconde dérivée, f'' qui est également dérivable. Le résultat final est 7 fois x moins 2, fois e de moins x. Comme l'exponentielle est positive, le signe dépend de x moins 2. La dérivée est positive pour x > 2 et négative pour x < 2. Nous concluons que la dérivée seconde change de signe en x = 2, ce qui indique un point d'inflexion.
Pour trouver les coordonnées de ce point d'inflexion, nous évaluons f(2) qui est égal à 14 moins 2, soit 12. Visuellement, sur le graphique de la fonction, on peut observer que la pente diminue avant le point d'inflexion, puis commence à augmenter après. La courbe de la dérivée seconde confirme cette observation.
Les points d'inflexion sont couramment utilisés en physique, notamment dans le titrage pour repérer un changement d'augmentation ou de diminution de la pente de la courbe. Cela conclut notre étude sur la convexité et les points d'inflexion.
N'hésitez pas à consulter la FAQ si vous avez d'autres questions.
Maths Spé
Analyse
Terminale

Continuité en un Point
Apprendre à trouver des dérivées de fonctions ayant plusieurs expressions sur des intervalles différents est l'objectif de cette méthode. On apprendra qu'une fonction peut être continue mais pas forcément dérivable, et dans ce cas, il est important de vérifier la continuité en différents points de la fonction. Pour qu'une fonction soit continue, elle doit d'abord être définie et ensuite, elle doit être continue sur tous les points de l'intervalle, y compris les extrémités. Pour vérifier cela, on doit regarder les limites à gauche et à droite de chaque point de l'intervalle, ainsi que la limite de la fonction en ce point. Si toutes les conditions sont remplies, la fonction est continue. Dans les prochaines étapes, on abordera la dérivation de cette fonction.
Maths Spé
Analyse
Terminale

Dérivabilité en un Point
La fonction étudiée dans ce cours est f(x) = |x|^2 + 2x - 3. On constate par observation graphique que cette fonction n'est pas dérivable en x = -3 et x = 1. On peut expliquer cela par le fait que la valeur absolue introduit une discontinuité de pente en ces points. Cependant, f(x) est dérivable sur l'ensemble des autres points de R. Cette dérivabilité peut être justifiée en montrant que f(x) est une composition de deux fonctions continues, à savoir un polynôme et la fonction valeur absolue.
Maths Spé
Analyse
Terminale

Prolongement par Continuité
Le prolongement par continuité est une méthode importante en mathématiques. Il est utilisé lorsque nous avons une fonction qui n'est pas définie en un point A, mais qui a une limite définie quand x tend vers A. Nous pouvons alors prolonger la fonction en A par continuité. Pour ce faire, nous posons f(A) égale à la limite de f(x) quand x tend vers A. Cela crée une fonction qui est définie et continue en A. Par exemple, la fonction f(x) égale x sur x n'est pas définie en 0, mais a une limite égale à 1. Nous pouvons prolonger cette fonction en faisant f(0) = 1. Dans l'exercice donné, la fonction proposée est f(x) égale à sinus 1 sur x pour x différent de zéro, et f(0) = 0. Nous devons prouver que cette fonction est bien continue en 0. Pour ce faire, nous utilisons le théorème d'encadrement en montrant que la valeur absolue de f(x) est encadrée entre 0 et x. Puis, nous prouvons que la valeur absolue de f(x) tend vers 0 quand x tend vers 0. En utilisant le théorème d'encadrement, nous montrons que la limite de f(x) quand x tend vers 0 est bien égale à 0, ce qui prouve que la fonction est bien continue en 0.En utilisant des méthodes mathématiques comme le théorème d'encadrement, nous pouvons prouver que les fonctions prolongées par continuité sont bien définies et continues.
Maths Spé
Analyse
Terminale

TVI et Fonction Auxiliaire
La méthode consiste à utiliser le théorème des valeurs intermédiaires pour étudier une fonction complexe. La fonction donnée est f(x) = 10x / (e^x + 1). On commence en calculant la dérivée de f(x), avec laquelle on obtient la fonction g(x) = 1 - xe^x. On vérifie que g(x) est continue sur l'intervalle [0,+∞], et qu'elle est strictement décroissante grâce à sa dérivée g'(x) = -xe^x < 0. En utilisant le théorème des valeurs intermédiaires pour les fonctions strictement monotones, on peut trouver un unique réel α tel que g(α) = 0. On détermine que α est compris entre 1,29 et 1,28. En utilisant le tableau de signes de la dérivée de f(x), on peut déduire le sens de variation de f(x), qui est croissante sur [0,α] et décroissante sur [α,+∞]. La fonction a un maximum en α et tend vers 0 en +∞. La stricte monotonie est importante pour assurer l'unicité de l'antécédent zéro, et donc pour appliquer le théorème des valeurs intermédiaires pour les fonctions strictement monotones.
Maths Spé
Analyse
Terminale
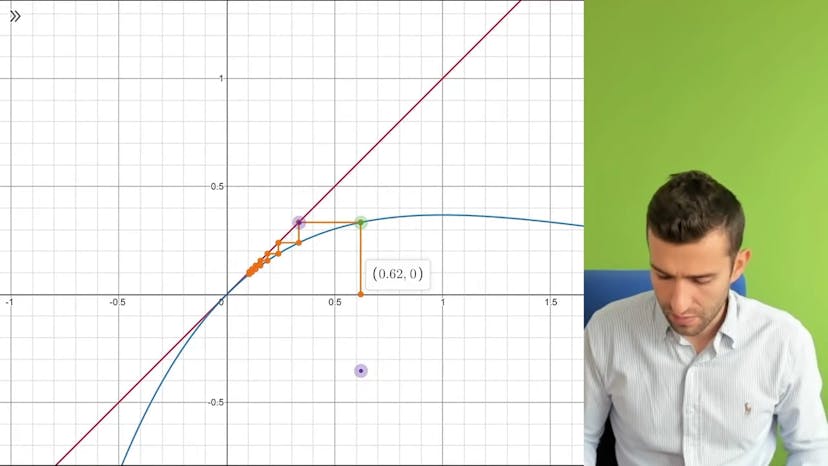
Continuité et suites 1
Dans cette méthode de calcul de limite avec suites définies par récurrence, il faut vérifier les hypothèses pour bien trouver la limite et la justifier. La suite est convergente vers une limite L si la relation de récurrence type un+1=f(un) vérifie que si la suite converge vers une limite L, alors un+1 converge aussi, en passant à la limite. Cela nécessite que f soit continue. En cherchant les points fixes, solutions de l'équation f(x)=x, on peut trouver la solution de la limite qui peut être unique ou multiple suivant la fonction f. Il faut alors être vigilant sur la continuité de f pour éviter les erreurs. Le premier terme de la suite est essentiel, car le comportement de la suite dépend de sa valeur. Si le premier terme est négatif et que la suite diverge, alors la solution de la limite est impossible.
Maths Spé
Analyse
Terminale

Continuité et Suites 2
Dans ce cours, nous étudions les suites définies par récurrence, en nous intéressant à leur limite. Nous commençons par associer une fonction f à la suite, telle que n+1 soit égal à f(n). Pour résoudre cette équation, nous devons étudier la continuité de f. Pour ce type d'exercice, la continuité de f est essentielle. Ensuite, nous résolvons l'équation f(x) = x pour trouver les valeurs possibles de la limite de la suite. Nous étudions également la dérivabilité de f. Il est important de noter que f peut ne pas être définie en certains points, ce qui impacte sa croissance. Nous passons ensuite à la démonstration par récurrence que 0.5 < u1 < u1+1 < 3. Nous utilisons la propriété de croissance de f pour composer avec l'hypothèse de récurrence. Nous concluons que la suite est croissante et bornée. En utilisant ces informations, nous déduisons que la suite converge vers une limite L. Enfin, nous soulignons l'importance de la continuité de f pour pouvoir affirmer que la limite est bien une solution de l'équation f(x) = x.
Maths Spé
Analyse
Terminale

Simplifier des expressions
Bienvenue dans ce cours sur les inéquations exponentielles et logarithmiques. Nous allons étudier les propriétés importantes pour résoudre ces équations. Pour la première équation ln(x) = 2, nous pouvons simplement composer avec l'exponentielle pour obtenir la solution x = e^2. Pour la deuxième équation e^x + 1 = 5, nous composons par le logarithme et trouvons x = ln(5) - 1. Pour la troisième équation 3ln(x) - 4 = 8, nous isolons le terme ln(x) avant de composer par l'exponentielle et obtenons x = e^(4/3). Pour les inéquations, nous devons toujours prendre en compte l'ensemble de définition. Par exemple, pour ln(6x - 1) > 2, nous composons par l'exponentielle pour obtenir la solution x > e^2 + 1/6. Pour e^x + 5 > 4e^x, nous rassemblons les termes exponentiels avant de composer par le logarithme et trouvons x < ln(5/3). Pour ln(x-3) + ln(9-x) = 0, nous combinons les termes ln pour obtenir ln((x-3)(9-x)) = 0, puis composons par l'exponentielle pour trouver les solutions x = 6 ± √8. Enfin, pour 3 - x > 0 et x + 1 > 0, nous résolvons l'inéquation ln(3-x)/(x+1) < 1 en multipliant par (x+1) et trouvons la solution x > 2. En résumé, il est important de prendre en compte l'ensemble de définition, de rassembler les termes en exponentiels ou en logarithmes et de composer par la fonction réciproque pour résoudre les équations et les inéquations exponentielles et logarithmiques.


