 All subjects
All subjects
 All subjects
All subjects
Maths
Analyse
Première

Calcul de termes arithmétiques
Ce cours explique la méthode fondamentale des suites arithmétiques et fournit des exemples. Une suite arithmétique est une suite où chaque terme est la somme du terme précédent et d'une constante appelée raison. Pour trouver un terme, il suffit d'ajouter la raison au terme précédent.Dans un exemple, on voit qu'une suite arithmétique a une raison de -4 et que le premier terme est 3. On peut alors calculer le deuxième terme en soustrayant 4 de 3, obtenant ainsi -1. Un autre exemple est donné avec une suite arithmétique où le quatrième terme est 5 et la raison est 5. On doit ajouter la raison 6 fois pour arriver au terme numéro 10. En utilisant cela, on peut trouver directement que le terme numéro 10 est égal au quatrième terme plus 6 fois la raison. Dans cet exemple, cela donne 5 plus 30, soit 35. C'est une méthode simple pour trouver n'importe quel terme dans une suite arithmétique en connaissant la raison et un ou plusieurs termes.
Maths
Analyse
Première

Calcul de termes géométriques
Ce cours explique la méthode fondamentale pour les suites géométriques. Il démarre par une question sur la suite géométrique de raison 3 avec U6 égal à 5 et demande de calculer U20. Pour passer d'un terme à l'autre, il suffit de multiplier le terme précédent par la raison. Ainsi, pour passer de U6 à U20, il faut multiplier U6 par 3 puissance (20-6), ce qui donne la réponse. La deuxième question concerne une suite géométrique de raison 2 et le premier terme est -6. La formule de la suite géométrique donne Vn = V0 fois la raison puissance n. Donc ici, Vn est égal à -6 fois 2 puissance n. La méthode principale à retenir est de comprendre qu'on peut sauter directement entre les termes en calculant la différence entre eux, comme dans le premier exemple.
Maths
Analyse
Première

Expression de termes d'une suite explicite
Une suite est une fonction qui prend comme antécédent l'ensemble des entiers naturels. Au lieu d'écrire "f de x", on peut écrire "u de n" ou "u indice n". Pour illustrer cela, prenons un exemple : définissons une fonction où pour tout entier naturel n, u égal au carré de n plus 1. Ainsi, si l'on considère u de 3, l'image de l'antécédent 3 par u sera 10.
Pour exprimer différentes expressions, reprenons l'expression de u et considérons-la comme u de quelque chose. Ainsi, u de quelque chose sera "chose au carré plus 1". En prenant "chose" égal à "n plus 1", l'expression reste la même et devient "n plus 1 au carré plus 1".
De même, pour u suivant, avec "chose" égal à "n moins 1", l'expression devient "n moins 1 au carré plus 1".
Pour u de z, l'expression reste toujours la même, c'est-à-dire "2z".
Enfin, pour u indice n plus 1, l'expression est "n carré plus 2".
Il est important de faire attention aux nuances et de ne pas confondre les expressions comme "un plus 1" où "n plus 1" est l'antécédent, et "un plus 1" où l'on ajoute simplement 1 à un.
Maths
Analyse
Première
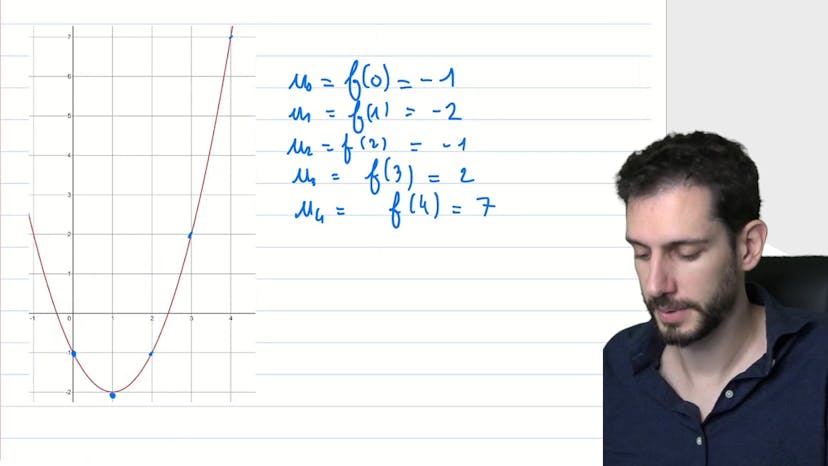
Lire des termes d'une suite explicite
Dans cette vidéo, nous traitons du lien entre une suite explicite et la représentation générale d'une fonction. Lorsque nous définissons explicitement une suite, nous ne considérons que certains antécédents et images d'une fonction définie sur R. Par exemple, la suite f2n est définie uniquement pour les entiers naturels, tels que n=0,1,2,3,4,5,6,7, et ainsi de suite. Pour déterminer les cinq premiers termes de la suite, nous recherchons f2 0, f2 1, f2 2, f2 3 et f2 4 sur le graphique. En lisant les coordonnées correspondantes sur le graphique, nous trouvons que u0 = f2 0 = -1, u1 = f2 1 = -2, u2 = f2 2 = -1, u3 = f2 3 = 2 et u4 = f2 4 = 7. Ainsi, la fonction associée à la suite peut prendre des valeurs négatives ou positives. Par exemple, la suite vn = racine de n + 2 peut donner des valeurs qui ne sont ni entiers naturels ni entiers relatifs. En résumé, une suite est une représentation discrète de points choisis à partir d'une fonction définie sur un ensemble de règles.
Maths
Analyse
Première

Application type des suites géométriques
Cet article explique l'utilisation des suites pour suivre l'évolution de données économiques ou démographiques. Le texte donne un exemple de ville qui a augmenté de 10% chaque année depuis 2018, pour montrer comment les suites peuvent être utilisées pour tracer ces évolutions. Le texte explique comment chaque terme de la suite peut être calculé, et justifie que cette suite est en réalité géométrique plutôt qu'arithmétique. Il explique également comment la raison de la suite peut être trouvée, et fournit des formules pour calculer chaque terme.
Maths
Analyse
Première

Somme de termes d'une suite arithmétique
Dans ce cours, nous calculons la somme des 25 premiers entiers naturels pairs. Pour résoudre cet exercice classique, nous utilisons nos connaissances sur les suites arithmétiques et géométriques, ainsi que sur les formules pour les sommes de termes de ces suites. Nous identifions rapidement que la somme est une suite arithmétique de raison 2. Nous écrivons la suite sous forme de combien de fois 2 chaque nombre est égal, en sachant que le 25ème terme est 24 fois 2 et non pas 25 fois 2. Nous appliquons la formule de la somme des n premiers entiers pour obtenir le résultat final : 300.
Maths
Analyse
Première

Somme de termes d'une suite géométrique
Dans cet exercice de mathématiques, il est demandé de calculer deux sommes. La première est une somme de termes d'une suite arithmétique et peut être résolue avec la formule générale où S est égal à 1 moins Q puissance le nombre de termes sur 1 moins Q. Dans cet exemple, Q est égal à 3 et le nombre de termes est 12. La deuxième somme est une somme de termes d'une suite géométrique, cependant, les termes ne sont pas donnés sous forme de puissance. En observant les alternances de signes, il est facile de comprendre que la raison est -2 et que le dernier terme est -2048. La formule générale est appliquée avec Q étant -2 et le nombre de termes étant 11. La somme finale est obtenue après des calculs mentaux simples.
Maths
Analyse
Première

Variations d'une suite - un peu bizarre !
Ce cours se concentre sur l'étude des variations de suites. La méthode principale est de calculer la différence entre deux termes successifs, soit un plus un moins un. Si le résultat est positif, cela signifie que le terme suivant est plus grand, et donc la suite est croissante. Si le résultat est négatif, cela signifie que le terme suivant est plus petit, et donc la suite est décroissante.
Dans cet exemple particulier, la suite est définie par u0 = 3 et un+1 = un + 1. En calculant un plus un moins un, on obtient un plus la racine carrée de n. Cette expression est positive ou nulle, ce qui signifie que la suite est croissante.
Dans un autre exercice, on cherche à déterminer la croissance de la suite vn+1 = 3/vn. En calculant vn plus un moins vn, on obtient 3 - vn^2 / vn. Dans ce cas, il n'est pas évident de trouver un résultat immédiatement. Donc, il est conseillé de calculer quelques termes de la suite pour avoir une idée de la croissance. En calculant les premiers termes, on remarque que la suite oscille entre les valeurs 1 et 3, et donc n'est ni croissante ni décroissante.
Il est important de ne pas paniquer lorsque l'on rencontre des difficultés dans la conclusion d'un problème. Calculer quelques termes de la suite peut souvent aider à se débloquer.
Maths
Analyse
Première

Application pratique de la somme des termes
Le cours porte sur l'application des suites arithmétiques à un problème pratique. Michael décide de faire un voyage à vélo de 2000 km de Paris à Stockholm. Le premier jour, il parcourt 20 km, puis chaque jour il ajoute 5 km de plus que la veille. Au bout de 10 jours, il a parcouru 400 km. Pour résoudre ce problème, on utilise les formules de suites arithmétiques. On note UN comme la distance parcourue le énième jour. On trouve que UN = 20 + (n-1) x 5, en utilisant la définition d'une suite arithmétique. Ensuite, on note SN comme la distance totale parcourue depuis le début. On utilise la formule de la somme des termes de la suite arithmétique pour exprimer SN en fonction de n. On obtient que SN = n/2 x (20 + (20 + (n-1) x 5)), ce qui simplifié donne SN = 35n + 5n^2/2.
Maths
Analyse
Première

Classique : suite auxiliaire
Ce cours traite d'un type de suite qui n'est ni une suite arithmétique ni une suite géométrique. Cette suite, appelée "suite arithmético-géométrique", est définie par récurrence en fonction de UN.
La méthode pour étudier cette suite consiste à étudier une autre suite, VN, qui est une version décalée de la première. On cherche alors à démontrer que cette suite VN est plus facile à étudier et qu'elle correspond à une suite géométrique.
Dans l'exercice, on donne les valeurs de U1 et U2, puis on demande de calculer V0. Ensuite, on cherche à démontrer que VN est une suite géométrique de raison 3 en calculant VN+1. En factorisant par 3, on obtient VN+1 = 3VN, ce qui permet de conclure que VN est bien géométrique de raison 3.
En déduisant l'expression de VN en fonction de N, on obtient VN = 4 * 3^N. Enfin, on déduit l'expression de UN en fonction de N en utilisant la relation UN = VN - 2. Ainsi, UN = 4 * 3^N - 2.
Il est recommandé de bien comprendre et maîtriser cet exercice, car il est très courant et peut tomber dans les évaluations. N'hésitez pas à poser des questions si nécessaire.
Maths
Analyse
Première

Variations d'une suite explicite
Ce cours présente une étude de variation de suite basée sur une suite explicite. L'approche utilisée ici consiste à exprimer la suite en termes d'une fonction f(x) = (x-3)/(2x+1) et à étudier les variations de cette fonction pour en déduire les variations de la suite. Pour simplifier l'expression de la fonction, on utilise une astuce consistant à inverser le numérateur et le dénominateur afin d'obtenir f(x) = 1/(2x+1) - 7/2. Cette fonction est une fonction inverse avec un signe moins, ce qui signifie qu'elle est décroissante. En conséquence, la suite est également décroissante. Cette approche permet de simplifier l'expression de la suite et est une alternative à la méthode habituelle utilisant des additions et des soustractions. En conclusion, la suite étudiée est décroissante.
Maths
Analyse
Première

Empilement de livres
Dans cet exercice, Pierre empile des livres de moins en moins épais en partant d'un livre de 500 pages. On cherche à déterminer combien de pages contient une pile de 20 livres. En utilisant la formule de la somme des termes d'une suite arithmétique, on obtient un résultat de 8100 pages pour la pile de 20 livres. Ensuite, on cherche le nombre maximum de livres que Pierre peut empiler si chaque livre doit contenir au moins 10 pages et on veut connaître le nombre total de pages de la pile. On trouve que le dernier livre doit être le 50ème et la pile va donc contenir 12 750 pages. L'exercice demande de bien poser le problème en mentionnant les termes de la suite arithmétique et en sachant appliquer les formules pour obtenir les résultats.


