Cours de Dérivation en Ligne par les Meilleurs Professeurs - Dérivation

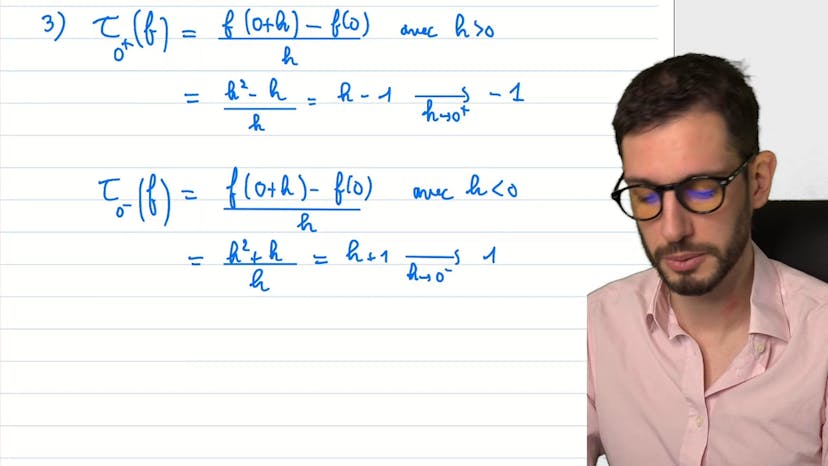
Une famille de fonctions !

Dans cette vidéo, il s'agit d'une transcription d'un cours sur une fonction avec une valeur absolue. Le professeur aborde plusieurs étapes pour étudier cette fonction. Tout d'abord, il explique que la valeur absolue pose des difficultés, notamment en ce qui concerne la tracé de la fonction et sa non-dérivabilité en zéro. Il propose donc de commencer par vérifier si la fonction est paire ou impaire, car cela peut permettre de réduire l'étude de la fonction à l'ensemble des réels positifs en utilisant une symétrie par rapport à l'axe Y. Dans cet exemple, la fonction est paire. Ensuite, le professeur propose d'écrire la fonction en utilisant différentes expressions sur différents intervalles pour se débarrasser de la valeur absolue. Il donne l'expression de la fonction pour les réels positifs (f(x) = x² - x) et pour les réels négatifs (f(x) = -x). Il explique également qu'il va tracer la fonction uniquement sur les réels positifs, mais qu'il a besoin de connaître l'expression sur les réels négatifs pour cela. Ensuite, le professeur aborde l'étude de la dérivabilité de la fonction. Il calcule le taux d'accroissement de la fonction en zéro en utilisant deux expressions différentes, une pour les réels positifs et une pour les réels négatifs. Il obtient deux limites différentes pour le taux d'accroissement en approchant zéro par la droite et par la gauche. Il conclut donc que la fonction n'est pas dérivable en zéro. Enfin, le professeur propose de continuer l'étude de la fonction sur l'ensemble des réels positifs. Il indique que la fonction est un polynôme du deuxième degré qui s'annule en zéro et en un. Il précise également que le maximum de la fonction se trouve en un demi. Il trace ensuite le graphe de la fonction sur les réels positifs, qui est une parabole. Il explique ensuite comment obtenir le graphe de la fonction sur les réels négatifs en utilisant une symétrie par rapport à l'axe des ordonnées. Il constate également la présence d'un point de non dérivabilité où la tangente a une pente de -1 d'un côté et une pente de 1 de l'autre côté. Il termine en notant que même si la fonction présente des points avec des "coins", on peut tout de même l'étudier et la tracer sans trop de difficultés. En conclusion, ce cours a abordé différentes étapes pour étudier une fonction avec une valeur absolue, notamment en vérifiant sa parité, en écrivant l'expression de la fonction sur différents intervalles, en étudiant sa dérivabilité et en traçant le graphe de la fonction.

Qui est f qui est f' sur un graphique ?

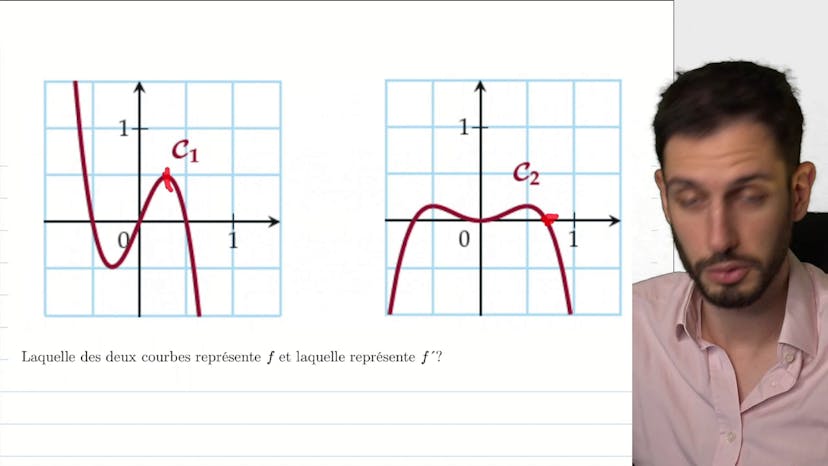
Ce cours explique la relation entre une fonction et sa dérivée. Lorsqu'une fonction est dérivable, elle est croissante si sa dérivée est positive et décroissante si sa dérivée est négative. Pour analyser deux graphes et déterminer lequel représente la dérivée, il suffit d'observer le signe de chaque fonction. Si la première fonction est positive jusqu'à (-0,5) et croit jusqu'à (-0,5), et que la seconde fonction est négative jusqu'à 0 et décroît jusqu'à 0, alors la première fonction est la dérivée. En revanche, si la première fonction est négative jusqu'à (-0,6) mais la seconde fonction décroît jusqu'à (-0,1), cela ne correspond pas à une dérivée. De plus, si la première fonction est positive de (-0,6) à 0, il faudrait qu'elle croisse entre les deux, ce qui n'est pas le cas. Finalement, si la première fonction devait décroître uniquement à partir de 0,7, cela ne correspondrait pas non plus. En conclusion, pour une fonction dérivable, on peut déterminer si elle croît ou décroît en observant le signe de sa dérivée.

Lien entre signe de f et de f' ?

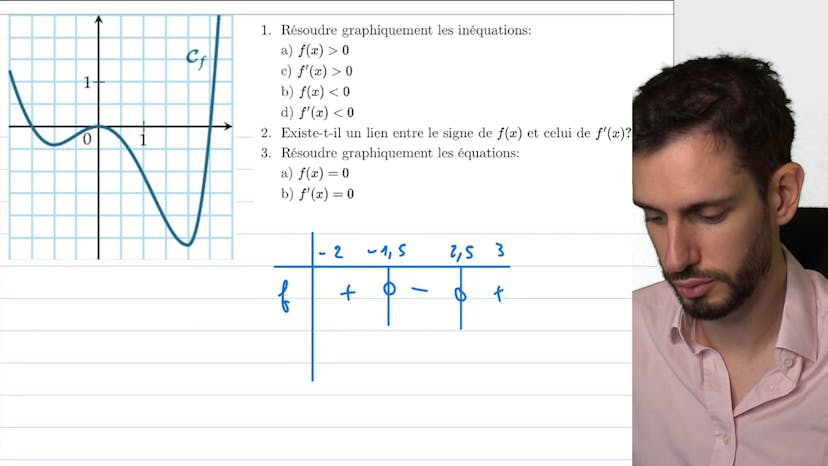
Ce cours aborde la résolution graphique des inéquations et met en évidence le lien entre la positivité de la fonction f(2x) et la croissance de sa dérivée f'(2x). Nous examinons les différentes régions où f(2x) est positif et négatif, ainsi que le signe de f'(2x) dans ces régions. Nous constatons qu'il n'y a pas de lien direct entre le signe de f(2x) et celui de f'(2x). Ensuite, nous résolvons graphiquement les équations f(2x) = 0 et f'(2x) = 0 en identifiant les points où la courbe touche l'axe des x et les points où la tangente à la courbe a une pente nulle. L'idée principale de cet exercice est de ne pas confondre les notions de positivité de la fonction et de sa dérivée, et de comprendre que différents scénarios sont possibles en termes de croissance de la fonction et du signe de sa dérivée.

Méthode COMPLETE pour étudier une fonction

En étudiant une fonction, il y a plusieurs étapes à suivre pour s'en sortir. Tout d'abord, il faut toujours vérifier l'ensemble de définition et faire attention aux racines et aux fractions. Ensuite, il est important de vérifier si la fonction est paire ou impaire, ce qui permet de simplifier l'étude. Si cela n'est pas possible, il est conseillé de vérifier si la fonction est trivialement croissante ou décroissante, car cela peut permettre de gagner du temps. Si cela ne fonctionne pas, il faut déterminer l'ensemble de dérivabilité et calculer la dérivée de la fonction. Il est ensuite important de déterminer le signe de la dérivée en fonction de x et de faire un tableau de variation en conséquence. Enfin, il est possible que des questions supplémentaires sur la convexité, les limites ou le tracé soient posées. En suivant cette méthode, il est possible de bien mener une étude de fonction et de ne pas se tromper.

Etude classique : une fonction inverse

Ce cours explique comment étudier une fonction typique en calcul différentiel. La fonction h est définie partout sur 5 par h2x égale 7-10 sur 5-x, et il faut justifier qu'elle est dérivable sur cet ensemble et déterminer sa fonction dérivée h'. Pour toute x différent de 5, h' de x est négatif strict, car il est égal à -10 divisé par un carré positif. Enfin, on peut dresser un tableau de variations de la fonction h en excluant la valeur interdite 5 et en notant que h' est toujours négatif et décroissant.

Etude classique : fonction cube

Dans ce cours, on étudie une fonction polynôme du troisième degré qui est dérivable sur R. On calcule la dérivée de cette fonction et on étudie son signe en utilisant les automatismes qui doivent être maîtrisés. Ensuite, on calcule les racines du polynôme et on détermine les variations de la fonction. Le cours insiste sur l'importance de connaître les polynômes du second degré car ce type d'exercice est très fréquent en mathématiques.

Optimisation et contraintes avec 2 réels

Dans ce cours, on apprend la méthode de dérivation pour résoudre des problèmes d'optimisation où l'on cherche à trouver la plus grande ou la plus petite solution possible avec des contraintes. On prend l'exemple de trouver les deux nombres dont le produit est minimal avec une différence de 100. On nomme les variables x et y, et on écrit le problème sous forme d'une fonction de deux variables. On utilise ensuite la contrainte pour éliminer y et obtenir une fonction de x seul, qui est un polynôme du second degré. Comme on veut trouver le minimum de cette fonction, on utilise la formule pour trouver le point de minimum, qui est x = -b/2a. En substituant cette valeur dans la fonction, on obtient la solution, qui est le produit minimal. La méthode consiste donc à nommer les variables, mettre le problème en équation, résoudre en utilisant les contraintes, et trouver le point de minimum/maximum pour la fonction.

Cône dans une sphère

Dans cette vidéo, le présentateur explique comment résoudre un problème mathématique impliquant la recherche du plus grand cône qui peut entrer dans une sphère. Il montre deux mises en équation différentes et explique que l'une est plus complexe que l'autre. Il donne des conseils sur la façon de poser les variables et montre comment calculer la dérivée pour trouver le maximum. Le présentateur souligne l'importance de faire attention à la mise en équation dès le départ car cela peut avoir des conséquences sur la résolution du problème. Finalement, il montre comment trouver la valeur de la variable qui rend le volume maximal.

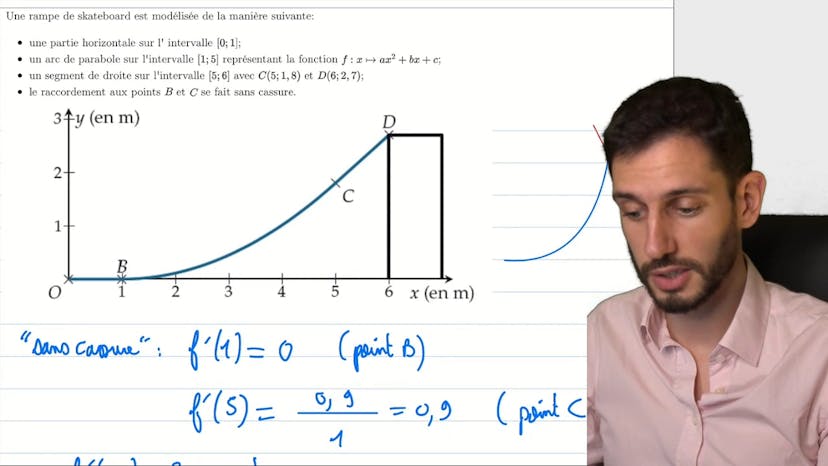
Piste de skate bien lisse

Dans ce cours, nous avons une rampe de skateboard modélisée par une fonction quadratique. La rampe comprend une partie horizontale, un arc de parabole et un segment de droite. L'objectif est de trouver les paramètres a, b et c de la fonction quadratique afin de garantir une transition sans cassure entre les différentes parties de la rampe. La notion de dérivation est essentielle pour comprendre cette transition sans cassure. La pente de la droite à raccorder doit être égale à la pente de la tangente à la courbe parabolique au point de raccordement. Pour résoudre le problème, il faut donc trouver les valeurs de a, b et c qui satisfont cette condition. En utilisant les coordonnées des points de raccordement, nous pouvons calculer les pentes des droites et établir un système d'équations. En trouvant les valeurs de a et b grâce à ce système, nous pouvons ensuite calculer la valeur de c. Ainsi, nous obtenons les paramètres nécessaires pour décrire la rampe de skateboard de manière continue et sans risque de chute. La clé de ce problème est de comprendre la relation étroite entre la notion de non cassure et la dérivabilité de la fonction. En comprenant cette relation, nous pouvons résoudre facilement le problème et obtenir une rampe de skateboard optimale.

Inégalité : poser une fonction !

Dans cet exercice de mathématiques, l'objectif est de démontrer qu'une expression en fonction de x est toujours plus grande que 2. Pour cela, deux méthodes sont proposées. La première consiste à poser une fonction f de x et à l'étudier pour montrer que f de x est toujours supérieure à 2. La seconde méthode utilise l'identité remarquable pour reconnaître que cette expression est égale à un carré parfait. Dans tous les cas, il s'agit de montrer que l'expression est positive ou nulle, ce qui permet de démontrer l'inégalité.

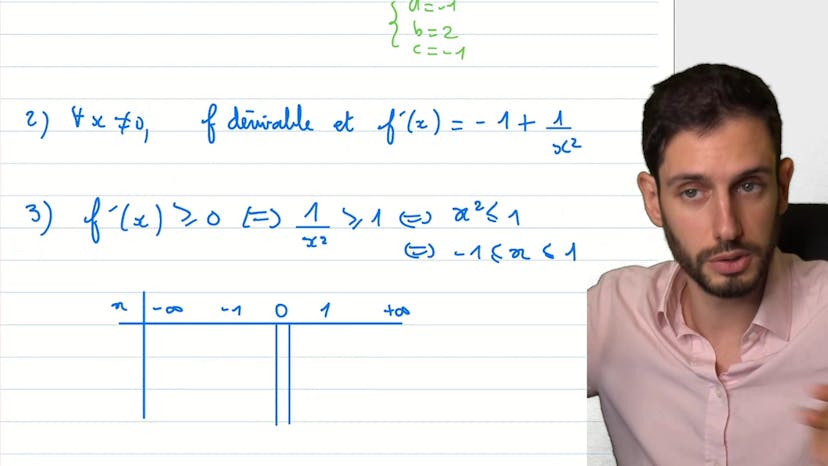
Une fraction à étudier et ses tangentes

Ce cours est une étude de fonctions avec dérivation. On nous demande de trouver la dérivée d'une fonction complexe et de déterminer les propriétés des tangentes à cette fonction. On applique les deux réflexes : simplifier la fonction et séparer le terme de x. On trouve que f(2x) = -x + 2 - 1/x, avec a = -1, b = 2 et c = -1. En dérivant cette fonction, on obtient f'(x) = -1 + 1/x^2. On étudie ensuite les variations de la fonction en utilisant des conditions de positivité. On trouve que f'(x) est positif ou nul pour x dans (-1,1). On met également en évidence la valeur interdite x = 0. On remarque que la tangente est horizontale pour x = -1 ou x = 1, et a une pente de 3 lorsque f'(x) = 3. On utilise ensuite la formule de la tangente pour trouver l'équation de la tangente aux points d'abscisses -2. On détermine ensuite les coordonnées des points d'intersection de la courbe avec les axes du repère en utilisant l'expression simplifiée de la fonction. On conclut en soulignant l'intérêt de remarquer des propriétés spécifiques de la fonction et en rappelant les différentes étapes de l'étude de fonction.

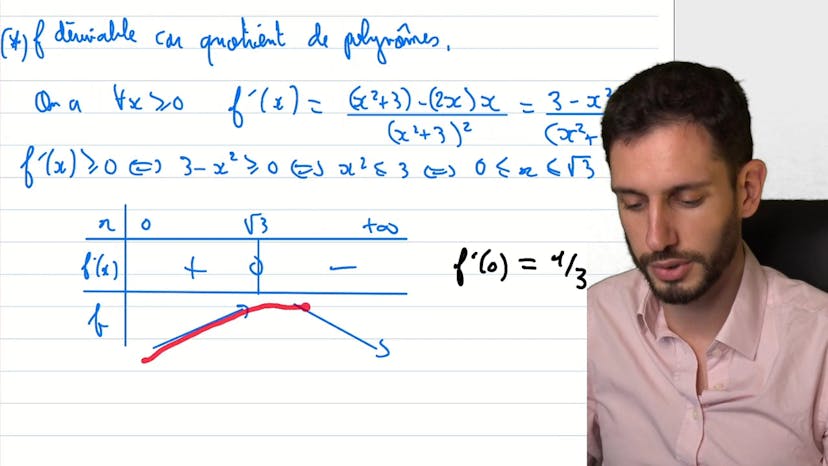
Fraction rationnelle et parité

Ce cours traite de l'étude d'une fonction classique, en partant de son énoncé. La première étape consiste à déterminer l'ensemble de définition de la fonction, qui est R (l'ensemble des nombres réels). Ensuite, on examine les variations de la fonction. Dans ce cas, la fonction est impaire, ce qui signifie qu'elle présente une symétrie par rapport à l'origine du repère. Grâce à cette propriété, on peut étudier la fonction uniquement sur le côté positif de l'axe des abscisses (R+), et ensuite appliquer une symétrie pour obtenir le comportement de la fonction sur le côté négatif (R-). Une remarque importante est que la fonction est dérivable car elle est le quotient de deux fonctions dérivables (ou polynômes). On utilise la formule de dérivation pour calculer la dérivée de la fonction et ensuite on étudie son signe. On obtient que la dérivée est positive ou nulle lorsque x est compris entre 0 et la racine carrée de 3. À partir de là, on peut tracer le graphique de la fonction en utilisant ces informations. Pour tracer correctement la courbe, il est conseillé de réaliser une étude plus approfondie en utilisant des notions de convexité et d'autres techniques avancées. Dans cet exemple, on se contente d'esquisser le graphique en indiquant qu'il y a un point maximum en 0 avec une pente de 1/3. Ensuite, la courbe descend jusqu'à tendre vers 0 lorsque x tend vers plus l'infini. Pour le côté négatif (R-), on fait simplement une symétrie par rapport à l'origine pour obtenir le comportement de la courbe. En résumé, le principal enseignement de ce cours est la possibilité d'utiliser la parité d'une fonction (pair ou impaire) pour simplifier son étude et gagner du temps. Ce concept permet de déterminer le comportement de la fonction sur R+ et ensuite d'appliquer une symétrie pour obtenir le comportement sur R-.

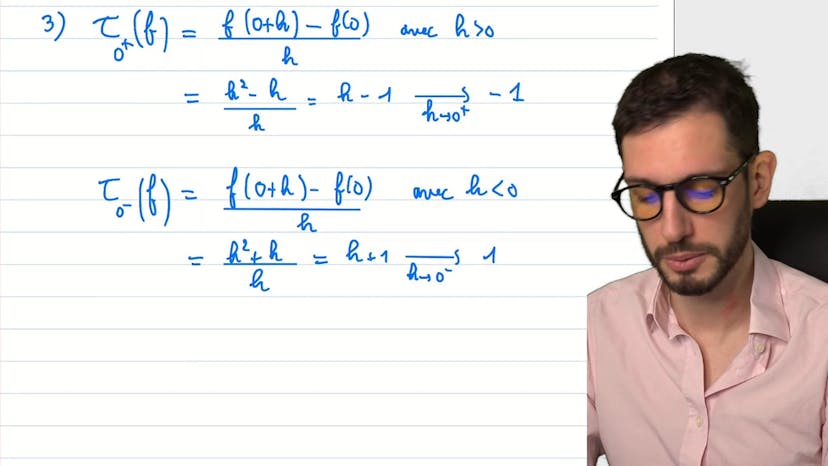
Valeur absolue et dérivabilité

Dans cette vidéo de mathématiques, l'objectif est d'étudier une fonction avec une valeur absolue et de déterminer si elle est paire ou impaire. Si la fonction est paire, on peut la réduire à l'étude de son domaine sur R+. Ensuite, pour se débarrasser de la valeur absolue, l'expression est écrite différemment sur différents intervalles. En étudiant le taux d'accroissement, on peut déterminer la non-dérivabilité de la fonction en 0. Enfin, sur R+, la fonction, un polynôme de degré 2, est tracée en tenant compte de sa non-dérivabilité en 0, ainsi que son symétrique sur R-.

Racine ET valeur absolue !

Ce cours d'analyse porte sur l'étude de la fonction f(x) qui contient une racine et une valeur absolue. On nous demande de trouver l'expression de f(x) sans valeur absolue, d'étudier sa dérivabilité et de tracer la courbe CF. Pour éliminer la valeur absolue, nous avons deux expressions à utiliser en fonction de la valeur de x. Pour étudier la dérivabilité en 1, nous trouvons deux pentes différentes, ce qui signifie que f(x) n'est pas dérivable en 1. Pour étudier les fonctions, nous dérivons f(x) en fonction de x et trouvons qu'elle est strictement croissante pour x inférieur ou égal à 1 et pour x supérieur ou égal à 5/4. Finalement, en traçant la courbe CF, nous voyons qu'il y a un point de rebroussement en 1 où la fonction n'est pas dérivable mais reste continue.

Hyperbole et construction géométrique

Dans cet exercice de dérivation et de géométrie, on doit montrer que la tangente en M à une hyperbole coupe les axes en deux points, dont M est le milieu. Pour cela, on utilise une formule de tangente en un point donné, on calcule les coordonnées des points d'intersection de la tangente avec les axes, puis on montre que le point M est bien le milieu de ces deux points. Enfin, on déduit un procédé de construction de la tangente en traçant une droite passant par les points d'intersection de la tangente avec les axes et passant par le point M. Cet exercice peut être source de compréhension des comportements de courbe de tangente en géométrie.