 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Introduction Primitives
Dans ce cours, nous abordons la notion de dérivé et la notion de dérivation. La dérivé nous donne accès à la pente des tangentes d'une courbe, ce qui nous permet de savoir si la courbe monte ou descend. Cependant, le but final de la dérivation est de déterminer quand une fonction est croissante, décroissante, ou quand elle atteint un maximum ou un minimum. Dans ce cours, nous allons inverser cette notion en nous demandant s'il existe une fonction dont la dérivée est égale à une autre fonction donnée. Cela s'appelle la primitivé.
Nous avons déjà appris plusieurs formules de dérivation en première année, et maintenant nous allons les utiliser dans l'autre sens pour trouver les primitives des fonctions. Il est important de noter que les constantes peuvent varier dans le processus de primitivation. Par exemple, si la dérivée d'une fonction est 2x, la primitive de cette fonction serait x^2, mais avec une constante de 2.
La primitivé a de nombreuses applications, notamment en physique, en chimie et en économie. En physique, nous pouvons utiliser la primitivé pour trouver la vitesse et la position d'un objet en fonction des forces qui s'appliquent sur lui. En chimie, nous pouvons étudier la vitesse de réaction de différentes substances. En économie, nous pouvons utiliser la primitivé pour optimiser les décisions d'investissement.
Dans ce chapitre sur les primitives, nous allons étudier la définition des primitives, leur existence, l'ensemble de leurs définitions, les conditions initiales et les primitives de fonctions composées. Nous allons également apprendre différentes méthodes pour déterminer les primitives, telles que transformer l'écriture d'une fonction pour obtenir les bonnes primitives.
En résumé, les primitives sont l'inverse de la dérivée et nous permettent de déterminer une fonction à partir de sa dérivée. Elles ont de nombreuses applications en sciences et en économie. Il est important d'apprendre les différentes formules de dérivation et de s'habituer à utiliser ces formules pour trouver les primitives des fonctions.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Primitive : Définition
Une primitive d'une fonction f est une fonction qui satisfait l'équation différentielle y' = f. Il s'agit d'une équation où l'inconnue est une fonction. Par exemple, la fonction exponentielle satisfait cette équation différentielle y' = y.
Le tableau de primitives est un outil classique qui permet de trouver les primitives de certaines fonctions. Il est important de noter que lorsqu'on décrit l'ensemble des primitives possibles, il faut toujours tenir compte d'une constante (notée k).
Certaines fonctions partagent les mêmes dérivées, ce qui signifie qu'elles ont les mêmes primitives. Par exemple, les fonctions 3x + 2 et 3x + 4 ont la même dérivée. Il est donc important de ne pas oublier cette constante lorsqu'on décrit l'ensemble des primitives.
L'exemple illustré montre la fonction f(x) = x² et une de ses primitives F(x) = x³/3. Il y a en réalité une infinité de fonctions primitives qui ressemblent à celle-ci, mais qui sont translatées vers le haut ou vers le bas.
Enfin, le cours se termine en présentant les formules de primitives à connaître par cœur, notamment celle pour x^n, 1/x^n et la formule du logarithme. Il est recommandé de bien les revoir pour pratique.
N'hésitez pas à poser des questions si vous avez des doutes ou consultez la FAQ. À la prochaine !
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Existence et Calcul des Primitives
Dans ce cours, nous abordons quelques théorèmes importants sur l'existence des primitives. Tout d'abord, le premier théorème stipule que toute fonction continue sur un intervalle admet des primitives sur cet intervalle. Par exemple, si nous prenons la fonction x², nous pouvons trouver plusieurs types de primitives tels que 3x+2, 3x+5, 3x-pi, etc. Une fois que nous avons trouvé une primitive, nous pouvons en trouver une infinité.
Cependant, il est important de noter que l'ensemble de toutes les primitives peut contenir d'autres fonctions que nous n'avons peut-être pas envisagées, mais dans cet exemple, nous avons montré qu'il y en a plus d'une.
Le deuxième théorème affirme que pour toute valeur y0 donnée, il existe une unique primitive qui passe exactement par ce point. Par conséquent, si nous fixons un point sur l'axe des ordonnées, il n'y a qu'une seule primitive qui passe par ce point. Par exemple, si nous fixons le point (0,5), il n'y a qu'une seule primitive qui vaudra F(0)=5. Il en va de même pour d'autres points donnés.
Il est important de démontrer ces théorèmes, car ils établissent une équivalence entre être une primitive et être de la forme F(x)+k. La démonstration consiste à utiliser une preuve par double implication, où l'on montre que les ensembles des primitives et des fonctions de la forme F(x)+k sont équivalents.
En outre, il existe un autre théorème important qui donne les règles de primitives pour des fonctions du type U'+V'. Par exemple, la primitive de U'+V' est U+V, et la primitive de λU' est λU, où λ est une constante. Il est important de mémoriser ces règles, tout comme on mémorise les règles de dérivation.
En conclusion, ces théorèmes sont essentiels pour comprendre l'existence des primitives et leurs propriétés. Il est important de les connaître et de comprendre comment les démontrer.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Primitives : condition initiale
Cet exercice porte sur la vérification des primitives d'une fonction présentée, ainsi que la détermination de l'ensemble des primitives et d'une condition initiale. La fonction f est donnée par f(x) = 3x² + 1/x. La première question consiste à vérifier si la fonction F, proposée comme x³ + ln(x), est une primitive de f. Pour cela, il suffit de dériver F et de voir si on obtient f. En dérivant, on obtient bien f(x). Donc F est une primitive de f. Cependant, il faut noter qu'il existe une infinité de primitives, définies à une constante additive près. Dans la deuxième question, on cherche à déterminer l'ensemble des primitives de F et à trouver celle qui prend la valeur 0 en E. Les primitives de F sont de la forme F(x) = x³ + ln(x) + K, où K est une constante réelle. Pour trouver la primitive qui s'annule en E, on utilise la condition initiale F(E) = 0. En substituant E dans F, on obtient l'équation K = -1 - E³. Ainsi, la primitive de F qui s'annule en E est F(x) = x³ + ln(x) - 1 - E³. Cet exercice introduit les méthodes sur les primitives, qui sont utiles pour la résolution des équations différentielles. Si vous avez des questions, n'hésitez pas à consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Transformer puis primitiver
Dans ce cours, nous allons voir comment trouver une primitive à partir d'une fonction pour laquelle il n'est pas évident de la trouver. La méthode consiste à identifier la fonction sous la forme d'un produit et à utiliser la décomposition en éléments simples pour les fonctions rationnelles.
Dans le premier exemple, la fonction étudiée est f(x) = 3x² + 2x³ + 2x. Nous cherchons à l'exprimer sous la forme "u' fois u". En observant la fonction, nous remarquons que nous pouvons prendre u(x) = x³ + 2x. En dérivant u(x), nous obtenons u'(x) = 3x² + 2, ce qui correspond exactement à la partie "u'" que nous cherchions. Ainsi, la fonction peut s'écrire comme u'(x) * u(x), où u(x) au carré serait une primitive de f(x).
En poursuivant, nous cherchons une primitive de f(x) qui prend la valeur 5 pour x = 1. Nous savons que les primitives sont de la forme f(x) + k, où k est une constante réelle. Nous imposons la condition que la primitive prenne la valeur 5 pour x = 1. Après calculs, nous trouvons que k = 1/2. Donc la fonction recherchée est 1/2 * x³ + 2x² + 1/2.
Dans le deuxième exemple, nous étudions une nouvelle fonction g(x) qui est également un produit, mais cette fois au dénominateur. Nous utilisons la méthode de décomposition en éléments simples pour transformer la fonction en une somme. Après calculs, nous trouvons que g(x) peut s'écrire comme -1/x + 1/(x-1).
Ensuite, nous cherchons la primitive de g(x). Nous calculons la primitive de chaque terme de la somme, ce qui nous donne -ln|x| + ln|x-1|. Cependant, il est important de noter que la primitive de 1/x est ln|x| pour x>0, et ln|x-1| pour x>1. Donc, pour éviter les valeurs absolues, nous pouvons écrire la primitive de g(x) comme ln(x) - ln(x-1) pour x>1.
En conclusion, ces deux méthodes nous permettent de trouver des primitives en identifiant des produits et en utilisant la décomposition en éléments simples pour les fonctions rationnelles.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Composition et Primitives
Dans cette vidéo, nous apprenons à repérer des primitifs de fonctions composées. Il est important de reconnaître certaines formes qui reviennent souvent. Par exemple, lorsque nous avons U' sur racine de U, nous savons que la primitive sera deux racines de U.
De même, lorsque nous avons cos U fois quelque chose, si c'est U', alors la primitive est sin U. Si nous avons U' fois sin U, la primitive sera moins cos U. Lorsqu'une exponentielle est présente, telle que U' fois E2U, la primitive est E2U. Si nous avons un coefficient du type U' sur U, alors la primitive est ln de U.
Lorsque nous avons U' fois U puissance n, la primitive est U puissance n plus 1 sur n plus 1. Pour être sûr de ne pas se tromper, nous pouvons proposer une primitive, la dériver et vérifier si nous obtenons la bonne fonction en retour. Si nous constatons un problème de facteur, nous pouvons ajuster notre proposition.
Pour U' sur U puissance n, la primitive est -1 sur n-1 fois 1 sur U puissance n-1. En résumé, nous diminuons le degré au dénominateur de la dérivation pour trouver la primitive.
Ensuite, nous examinons les opérations inverses, telles que la racine de U dont la dérivée est U' de racine de U. Comprendre ces opérations inverses nous permet de trouver plus facilement les primitives des fonctions composées.
La constante multiplicative n'est pas un problème. Si nous avons une constante incorrecte, nous pouvons simplement la décomposer et ajuster notre valeur. Finalement, nous mettons en pratique ces méthodes pour déterminer les primitives d'une fonction donnée.
Dans l'exemple donné, nous devons trouver toutes les primitives sur R de la fonction exponentielle de U. Nous remarquons que la dérivée de notre fonction est 6x, donc nous devons ajouter le facteur 6 pour obtenir la bonne forme. Ainsi, les primitives de la fonction sont de la forme E de 3x² plus 5, multipliée par 1/6 et ajoutée à une constante. En résumé, nous pouvons trouver les primitives d'une fonction composée en reconnaissant les formes courantes et en ajustant si nécessaire.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
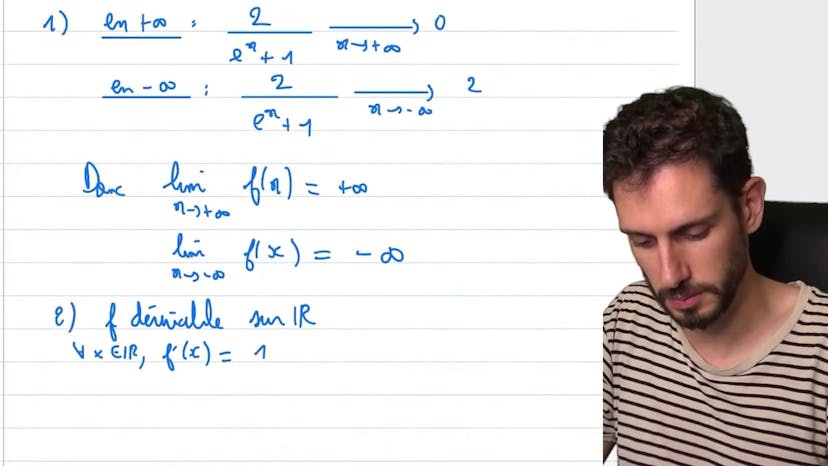
Primitive et réécriture
Dans ce cours, nous étudions une fonction définie par f2x = x + log(4) + 2/(e^(2x) + 1). Nous commençons par analyser cette fonction pour essayer de trouver une expression de primitive facile à détecter. Nous calculons la limite de la fonction lorsque x tend vers l'infini et nous obtenons 0. Pour x tendant vers moins l'infini, la limite est de 2. Ensuite, nous étudions le sens de variation de la fonction et dressons le tableau de variation. Nous montrons que la fonction est dérivable sur R et nous calculons sa dérivée f'2x. En analysant le signe de cette dérivée, nous concluons que f'2x est toujours positif. Par conséquent, la fonction f2x est croissante sur l'ensemble des réels.
Pour déterminer les primitives de la fonction, nous remarquons que x et log(4) sont communs dans les différentes expressions de la fonction. Nous obtenons donc une primitive sous la forme x²/2 + (2 + log(4))x. De plus, nous reconnaissons une expression de la forme -2(e^(2x)/(e^(2x) + 1)), que nous pouvons intégrer en utilisant le logarithme. Nous obtenons ainsi une expression de primitive de la forme logarithme de (e^(2x) + 1) + K, avec K appartenant à R.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
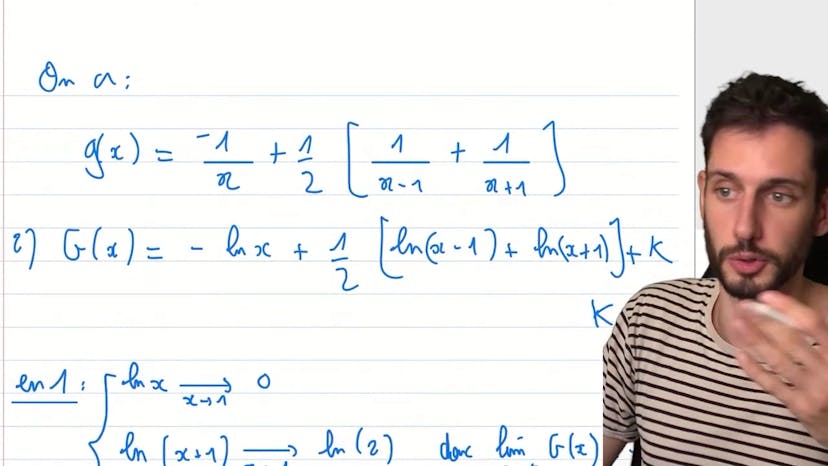
Décomposition en éléments simples
"En MathSup, on apprend à simplifier les fractions rationnelles. On peut le faire de deux façons : en mettant tout au même dénominateur ou en utilisant une méthode plus efficace. Cette méthode consiste à prendre les valeurs de x qui annulent certains termes pour isoler les constantes. En appliquant cette technique, on peut trouver rapidement les constantes a, b et c. Ensuite, on peut déterminer l'ensemble des primitifs de la fonction et ajouter une constante k. Enfin, on peut trouver la limite de la primitive en plus infini et en 1. En utilisant les propriétés du logarithme, on peut réécrire la fonction de manière plus simple. La limite de la fonction tend vers 0, peu importe la constante k."
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Polynôme × exponentielle
Ce cours explique comment trouver la primitive d'une fonction contenant une exponentielle. En général, si la fonction est un polynôme multiplié par une exponentielle, sa primitive sera probablement un polynôme du même degré multiplié par l'exponentielle. On apprend également les règles générales de relations entre les primitives et les fonctions. La question 1 demande de trouver la dérivée de la primitive de moins 1, qui est simplement la fonction elle-même. La question 2 demande d'exprimer la dérivée de la fonction en fonction de x, en utilisant les paramètres a et b trouvés dans la question 1. La question 3 demande d'identifier les paramètres a et b en égalant les deux polynômes de la question 2. On trouve que a est égal à moins 1 et b est égal à 3. En utilisant ces valeurs, on trouve que la dérivée de la fonction est moins x plus 3, moins x2 plus 3x, et moins 2x.
Révisions Maths lycée
Analyse Terminale
BCPST

Introduction Primitives
Avant d'aborder les primitives, il est rappelé que la dérivation permet d'accéder à la pente des tangentes, ce qui permet de déterminer si une courbe monte ou descend. Cependant, une autre question se pose: existe-t-il une fonction dont la dérivée est égale à une fonction donnée ? C'est là qu'intervient la notion de primitive, qui est une sorte d'anti-dérivation. En d'autres termes, la primitive permet de passer de la fonction dérivée à la fonction elle-même. Pour trouver les primitives, on utilise un tableau similaire à celui utilisé pour les dérivées, mais à l'envers. En pratique, il faudra prendre en compte des constantes supplémentaires et effectuer des manipulations supplémentaires pour obtenir la bonne réponse. Cette notion de primitive est utilisée dans de nombreux domaines, tels que la physique, la chimie et l'économie, notamment pour trouver la vitesse, l'accélération et la position d'un objet en fonction des forces qui lui sont appliquées. En résumé, les primitives permettent de trouver la fonction dont la dérivée est égale à une fonction donnée, et sont utilisées dans de nombreux domaines pour résoudre différents problèmes.
Révisions Maths lycée
Analyse Terminale
BCPST

Primitive : Définition
Une fonction primitive de f est une solution de l'équation différentielle y'=f. On peut définir une fonction F comme primitive de f si, pour tout x dans l'intervalle de définition, F'(x) = f(x). Une équation différentielle est une équation où l'inconnue est une fonction. Par exemple, l'exponentielle est une fonction qui vérifie y'=y. Pour trouver les primitives d'une fonction, on utilise le tableau de primitives, qui est l'inverse du tableau de dérivées. Chaque primitive a une constante ajoutée, car la dérivée d'une constante est nulle. Il est important de ne pas oublier cette constante lorsqu'on décrit l'ensemble des primitives possibles. De nombreuses fonctions peuvent avoir la même dérivée, ce qui signifie qu'elles partagent les mêmes primitives. Une illustration montre que la fonction x² est une primitive de x³/3, avec différentes constantes ajoutées. Le tableau de primitives se termine par des formules à connaître par cœur, comme x^n+1/n+1 + k pour toutes les valeurs de n, ou 1/x^n pour n différent de 1 (qui devient log(x) lorsque n=1). Il est important de bien connaître ces formules. La transcription se termine en invitant les spectateurs à poser des questions et en disant au revoir.
Révisions Maths lycée
Analyse Terminale
BCPST

Existence et Calcul des Primitives
En résumé, ce cours porte sur les théorèmes importants concernant l'existence des primitives. Le premier théorème énonce que toute fonction continue sur un intervalle a des primitives sur cet intervalle. Par exemple, pour la fonction 3 constante, on peut trouver une infinité de primitives comme 3x plus 2, 3x plus 5, etc. Le deuxième théorème énonce que l'ensemble de toutes les primitives d'une fonction f est égal à l'ensemble des fonctions F plus une constante K. Ce théorème montre qu'il n'y a pas d'autres primitives que celles de la forme F plus K. Le troisième théorème indique que pour chaque valeur de y0, il existe une unique primitive qui passe par ce point. En utilisant ces théorèmes, on peut déterminer les primitives de fonctions et effectuer des calculs. Le cours se termine en présentant un tableau des primitives, similaire au tableau des dérivées, qui permet de calculer les primitives de différentes fonctions.
Révisions Maths lycée
Analyse Terminale
BCPST

Primitives : condition initiale
Dans cet exercice, nous devons vérifier si la fonction F(x) = x³ + ln(x) est une primitive de la fonction f(x) = 3x² + 1/x. Pour cela, nous devons dériver F(x) et vérifier si nous obtenons f(x). En dérivant F(x), nous obtenons 3x² + 1/x, ce qui est bien égal à f(x). Donc F(x) est une primitive de f(x).
Il est important de noter qu'il existe une infinité de primitives de f(x), car il y a une constante additive qui peut varier. La question suivante consiste donc à trouver l'ensemble des primitives de F(x) et à déterminer celle qui prend la valeur 0 en un point donné E. Pour cela, nous avons trouvé que les primitives de F(x) sont de la forme F(x) = x³ + ln(x) + K, où K est une constante réelle.
Pour trouver la primitive qui s'annule en E, nous devons trouver la valeur de K qui satisfait F(E) = 0. En remplaçant x par E dans F(x), nous obtenons E³ + 1 + K = 0. En résolvant cette équation, nous trouvons que K = -1 - E³. Donc la primitive de F(x) qui s'annule en E est F(x) = x³ + ln(x) - 1 - E³.
Cet exercice introduit les méthodes de calcul des primitives et montre leur utilité dans la résolution des équations différentielles. Si vous avez des questions, n'hésitez pas à les poser dans la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Transformer puis primitiver
Dans ce cours, nous étudions comment trouver une primitive d'une fonction pour laquelle il n'est pas évident de la trouver initialement. Nous remarquons que dériver une fonction est toujours facile, mais trouver une primitive peut être compliqué. Dans notre exemple, nous avons une fonction f(x) = 3x^2 + 2x^3 + 2x, et nous cherchons à l'exprimer sous la forme u' * u. En identifiant u(x) = x^3 + 2x, nous remarquons que u'(x) = 3x^2 + 2, ce qui correspond exactement au terme dans la fonction f(x). Ainsi, la fonction f(x) peut être exprimée comme la dérivée presque exacte de u^2(x). Nous retenons qu'une constante multiplicative dans une primitive n'est pas un problème. En dérivant u^2(x), nous obtenons 2u'(x)u(x), soit 2(x^3 + 2x). En ajoutant la constante 1/2, nous obtenons notre primitive de f(x), qui vaut (1/2)(x^3 + 2x)^2. Ensuite, nous cherchons la primitive qui vaut 5 quand x = 1. Nous savons que les primitives sont de la forme f(x) + k, où k est une constante réelle. Pour trouver k, nous utilisons l'équation f(1) + k = 5. En résolvant l'équation, nous trouvons que k = 1/2. Ainsi, la fonction recherchée est (1/2)(x^3 + 2x)^2 + 1/2. Dans la seconde partie du cours, nous étudions une nouvelle fonction g(x) qui est un produit au dénominateur. Nous utilisons une méthode classique pour les fonctions rationnelles, c'est-à-dire la décomposition en éléments simples. En trouvant les réels a et b tels que g(x) = a/x + b/(x-1), nous obtenons a = -1 et b = 1. Ainsi, g(x) équivaut à (-1/x) + (1/(x-1)). Trouver une primitive devient beaucoup plus simple dans ce cas, car nous avons une somme de termes faciles à identifier. La primitive de -1/x est -ln|x| et la primitive de 1/(x-1) est ln|x-1|. En regroupant ces deux termes, nous obtenons notre primitive de g(x), qui est -ln|x| + ln|(x-1)|. Il faut faire attention à l'intervalle de définition, qui exclut les valeurs de x pour lesquelles la fonction n'était pas définie. Enfin, nous mentionnons qu'une primitive de 1/x est ln|x|, avec la condition que x soit strictement positif. Si nous voulons nous débarrasser des valeurs absolues, nous pouvons écrire la primitive comme ln(x) - ln(-x). Il est important de noter que pour une fonction avec des intervalles de définition multiples, il est possible que les primitives aient des expressions différentes selon l'intervalle. C'est le cas de 1/x, qui a une expression différente pour R+ et R-. Cela conclut notre cours sur ces deux méthodes de calcul de primitives.
Révisions Maths lycée
Analyse Terminale
BCPST

Composition et Primitives
Dans cette méthode, nous apprenons à repérer des primitifs de fonctions composées. Certaines formes reviennent fréquemment en maths, comme U' sur racine de U, qui a une primitive de deux racines de U. De la même manière, cos U fois quelque chose a une primitive de sin U, et U' fois sin U a une primitive de moins cos U. L'exponentielle U' fois E2U a une primitive de E2U, et U' sur U a une primitive de ln de U. U' fois U puissance n a une primitive de U puissance n+1 sur n+1. Si la fonction a la forme U' sur U puissance n, la primitive est -1 sur n-1 fois 1 sur U puissance n-1. Ces formules peuvent être utiles pour reconnaître rapidement des primitives. La méthode d'opération inverse consiste à proposer une primitive, la dérivée, puis vérifier si elle correspond à la fonction d'origine. Pour les racines de U, la dérivée est U' sur la racine de U. Enfin, pour trouver la constante multiplicative, une simple décomposition peut aider à déterminer la bonne valeur. Dans un exemple pratique donné, il est demandé de trouver toutes les primitives de la fonction exponentielle de 3x²-5. Bien qu'il manque le 6 devant U', on peut l'introduire en décomposant le x en 1/6x fois 6x. Ainsi, les primitives de la fonction sont de la forme E de 3x² plus 5, avec une constante multiplicative de 1/6. Finalement, il est important de noter que les primitives sont définies à une constante près, mais une condition particulière peut être utilisée pour déterminer précisément cette constante.
Révisions Maths lycée
Analyse Terminale
BCPST
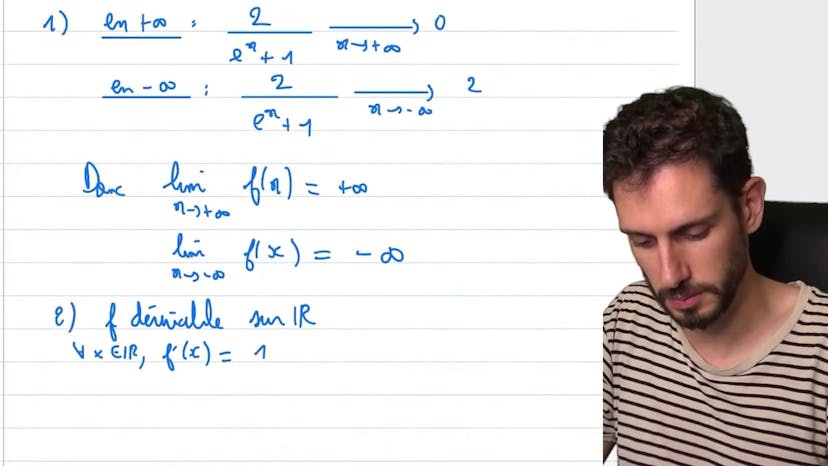
Primitive et réécriture
Dans ce cours, nous sommes présentés à une fonction définie par f2x = x + log(4) + 2/(e^(2x) + 1). Nous nous concentrons sur la recherche d'une expression de primitive pour faciliter notre travail.
• Nous commençons par calculer les limites en plus et moins infini. Lorsque x tend vers plus l'infini, f2x tend vers la limite de x, qui est également plus l'infini. Lorsque x tend vers moins l'infini, f2x tend vers 2.
• En analysant la variation de f, nous montrons que f est dérivable sur R car elle est la somme d'un polynôme de degré 1 (x + log(4)) et d'une fraction où les deux fonctions sont dérivables.
• En dérivant f2x, nous arrivons à f'2x = 1 - 2e^(2x)/(e^(2x) + 1)^2. Nous étudions le signe de f'2x et concluons qu'il est toujours positif. En d'autres termes, f est croissante sur R.
• En réécrivant f2x, nous remarquons que x et log(4) sont communs aux deux expressions. Il ne reste plus qu'à montrer que 2 - 2e^(2x)/(e^(2x) + 1) est équivalent à cette différence. En simplifiant cette expression, nous obtenons la primitive de f, qui est x^2/2 + (2 + log(4))x - 2ln(e^(2x) + 1) + K, où K est une constante réelle.
Ainsi, nous avons trouvé l'ensemble des primitives possibles de cette fonction.
Révisions Maths lycée
Analyse Terminale
BCPST
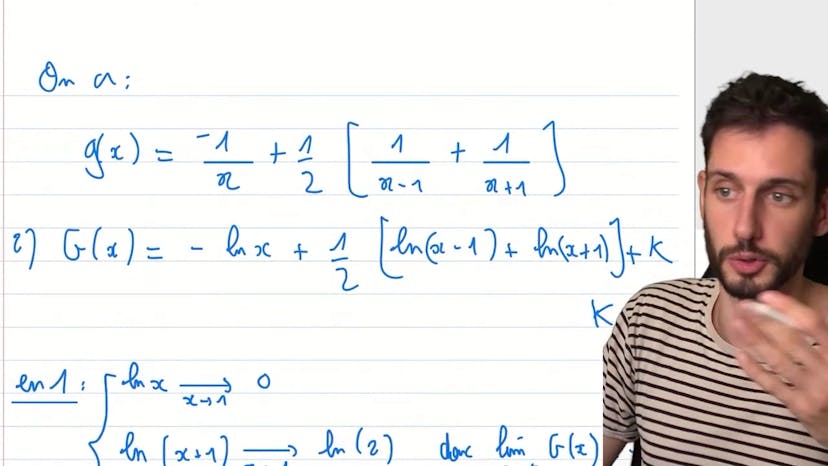
Décomposition en éléments simples
Dans ce cours, on apprend à simplifier les fractions rationnelles de fonctions polynomiales. On peut utiliser deux méthodes, mais on préfère la méthode la plus simple. On cherche à trouver les constantes a, b et c telles que g(x) soit égal à une certaine expression donnée. Plutôt que de les identifier en mettant tout au même dénominateur, on utilise une méthode plus efficace. On prend successivement les valeurs de x, x+1 et x-1 pour isoler a, b et c. Ainsi, on obtient les valeurs des constantes sans avoir à résoudre un système d'équations complexe. En pratique, cela se fait en 2 minutes environ. Ensuite, on étudie les primitives de g(x) et leur limite en +∞ et en 1. On détermine que la limite du logarithme de (x-1)/(x+1) quand x tend vers 0 est -∞. On combine les logarithmes de g(x) en utilisant la propriété log(a) + log(b) = log(a*b). On intègre 1/2 log(x) = log(√x), et on réarrange les termes pour obtenir une expression simplifiée de g(x). On conclut en disant que la limite de g(x) quand x tend vers +∞ est indéterminée (notée grand k).
Révisions Maths lycée
Analyse Terminale
BCPST

Polynôme × exponentielle
En résumé, ce cours traite de la recherche d'une primitive d'une fonction exponentielle multipliée par un polynôme. On applique la règle générale selon laquelle la primitive d'un polynôme multiplié par une exponentielle est un polynôme du même degré multiplié par l'exponentielle. Le résultat recherché est donc une fonction de la forme ax^2 + bx + c multipliée par l'exponentielle x. En utilisant cette règle, on dérive la fonction F' de x pour obtenir F' de x = -x + 3 -x^2 + 3x -2x. En résolvant les équations résultantes, on obtient les valeurs a = -1 et b = 3, ce qui nous donne F' de x = -x + 3 -x^2 + 3x -2x.
Révisions Maths lycée
Analyse Terminale
ECG

Introduction Primitives
Dans cette vidéo, on aborde la notion de primitive en mathématiques, qui est liée à la dérivation. La dérivée permet de calculer la pente des tangentes à une courbe, ce qui permet de déterminer si la courbe monte ou descend. En revanche, la primitive recherche une fonction dont la dérivée est égale à une autre fonction donnée. On peut voir cela comme une sorte d'anti-dérivation.
Pour trouver des primitives, on utilise un tableau de dérivation que l'on inverse. Par exemple, si la dérivée de xn est n fois x^(n-1), alors la primitive de 2x est x^2. Cependant, parfois il faut ajuster les coefficients.
Les applications des primitives sont nombreuses, notamment en physique, chimie et économie. En physique, on peut utiliser les primitives pour retrouver la vitesse et la position d'un objet à partir de son accélération. En chimie, cela peut servir à étudier la vitesse de réaction. En économie, les primitives peuvent permettre d'optimiser les décisions d'investissement.
Dans ce chapitre sur les primitives, on étudiera la définition, l'existence, les méthodes de détermination et les propriétés des primitives. Il faudra apprendre les tableaux de dérivation de première année avec quelques nuances. Les méthodes consistent à transformer l'écriture d'une fonction pour obtenir les bonnes primitives et à déterminer les primitives des fonctions composées.
En résumé, les primitives sont des fonctions dont les dérivées sont égales à d'autres fonctions données. Elles sont utilisées dans différentes disciplines scientifiques et économiques. Pour trouver des primitives, on utilise un tableau de dérivation inversé. Il est recommandé d'apprendre les tableaux de dérivation de première année et de s'entraîner à retrouver les bonnes primitives.
Révisions Maths lycée
Analyse Terminale
ECG

Primitive : Définition
Le cours explique les notions de primitive et d'équation différentielle de manière simple. Une primitive d'une fonction définie sur un intervalle i réel est une fonction qui est solution de l'équation différentielle y' = f. L'équation différentielle est une équation où l'inconnue est une fonction. Par exemple, la fonction exponentielle vérifie l'équation y' = y. Le cours mentionne également le tableau de primitives, qui est le tableau inverse de la dérivée. Il est important de retenir que les primitives peuvent différer par une constante. Enfin, le cours présente une illustration avec la fonction f(x) = x² et sa primitive F(x) = x³/3. Cette primitive représente une famille de fonctions ayant la même valeur dérivée. La fin du cours énumère quelques formules de primitives à connaître par cœur.
Révisions Maths lycée
Analyse Terminale
ECG

Existence et Calcul des Primitives
En résumé, ce cours traite des théorèmes importants sur l'existence des primitives. Le premier théorème stipule que toute fonction continue sur un intervalle admet des primitives sur cet intervalle. Par exemple, la fonction constante 3 a plusieurs primitives, telles que 3x+2, 3x+5, 3x-7, etc. Le deuxième théorème affirme que l'ensemble de toutes les primitives d'une fonction continue est équivalent à l'ensemble des fonctions de la forme "F(x) + k", où F(x) est la première primitive considérée et k est une constante. Finalement, le troisième théorème indique que pour chaque valeur y0 fixée sur l'axe des ordonnées, il existe une unique primitive qui passe exactement par ce point. Ces théorèmes permettent notamment de démontrer les propriétés des primitives et de simplifier leur étude.
Révisions Maths lycée
Analyse Terminale
ECG

Primitives : condition initiale
Dans cet exercice, nous devons vérifier si la fonction proposée, F(x) = x³ + ln(x), est une primitive de la fonction f(x) = 3x² + 1/x. Pour cela, nous dérivons F(x) et vérifions si nous obtenons f(x). En dérivant F(x), nous obtenons 3x² + 1/x, ce qui correspond à f(x). Donc, F(x) est bien une primitive de f(x).
Il est important de noter ici que F(x) est une primitive de f(x), mais il existe une infinité de primitives définies à une constante additive près. Nous devons donc trouver l'ensemble des primitives de F(x) et déterminer celle qui prend la valeur 0 pour la condition initiale E.
L'ensemble des primitives de F(x) est donné par F(x) + K, où K est une constante réelle. Donc, les primitives de F(x) sont de la forme F(x) + K = x³ + ln(x) + K.
Pour trouver la valeur de K qui fait que la primitive s'annule en E, nous évaluons la primitive en E et résolvons F(E) + K = 0. En calculant F(E), nous obtenons E³ + 1 + K. Donc, pour que cette équation soit vérifiée, K doit être égal à -1 - E³.
Ainsi, la primitive de F(x) qui s'annule en E est x³ + ln(x) - 1 - E³.
Cet exercice introduit les méthodes de calcul des primitives, qui sont indispensables pour la résolution des équations différentielles. Si vous avez des questions, n'hésitez pas à les poser dans la FAQ. C'est une méthode importante à connaître.
Révisions Maths lycée
Analyse Terminale
ECG

Transformer puis primitiver
Dans cette vidéo, nous apprenons comment trouver une primitive d'une fonction lorsque celle-ci n'est pas évidente à trouver. La dérivation est facile, mais trouver une primitive peut être compliqué. Nous allons étudier le cas d'un produit où il peut être difficile de trouver la primitive.
La fonction que nous étudions est f(x) = 3x^2 + 2x^3 + 2x. Nous allons essayer de l'identifier sous la forme u' * u. En choisissant u(x) = x^3 + 2x, nous pouvons dériver u et obtenir u'(x) = 3x^2 + 2, ce qui correspond à notre fonction.
Une primitive de u'(x) * u(x) est donc (1/2) * (u(x))^2, ce qui donne (1/2) * (x^3 + 2x)^2.
Ensuite, nous voulons trouver une primitive qui prend la valeur 5 lorsque x = 1. Nous utilisons la formule des primitives qui sont toutes de la forme f(x) + k, où k est une constante réelle. Nous pouvons résoudre cette équation en substituant les valeurs et trouver que k = 1/2.
Finalement, la fonction recherchée est (1/2) * x^3 + 2x^2 + 1/2.
Ensuite, nous étudions une nouvelle fonction g qui est un produit avec un dénominateur. Pour traiter ce cas, nous utilisons une méthode classique de décomposition en éléments simples. Nous trouvons les réels a et b tels que g(x) = a/x + b/(x-1). En regroupant les termes et en identifiant les coefficients, nous obtenons a + b = 0 et -a = 1. Nous résolvons ce système d'équations pour trouver a = -1 et b = 1.
La fonction g(x) devient donc -1/x + 1/(x-1).
Pour trouver la primitive de cette fonction, nous calculons la primitive de chaque terme séparément. La primitive de -1/x est -ln|x| et la primitive de 1/(x-1) est ln|x-1|. La fonction proposée -ln|x| + ln|x-1| est donc une primitive de g(x).
Il est important de noter que pour le domaine de définition de g, qui est de 1 à l'infini, la primitive est définie à partir de 1 en raison du terme ln|x-1|. De plus, la primitive de 1/x est ln|x| en valeur absolue, car elle n'est pas définie pour les valeurs négatives de x.
En conclusion, nous avons appris deux méthodes pour calculer des primitives : l'identification d'un produit sous la forme u' * u et la décomposition d'une fonction rationnelle en éléments simples.
Révisions Maths lycée
Analyse Terminale
ECG

Composition et Primitives
Dans ce cours, nous apprenons à repérer des primitifs de fonctions composées. Certaines formes reviennent fréquemment et il est important de les reconnaître. Par exemple, si nous avons U' sur la racine de U, la primitive sera de deux racines de U. De même, si nous avons cos U fois quelque chose, si c'est U', la primitive sera sin U. Si nous avons U' fois sin U, la primitive sera moins cos U. Si nous avons U' fois E2U, la primitive sera E2U. Si nous avons U' sur U, la primitive sera ln de U. Si nous avons U' fois U puissance n, la primitive sera U puissance n plus 1 sur n plus 1.
Il est important de vérifier nos calculs en dérivant la proposition de primitive et en vérifiant si nous obtenons la bonne fonction. Parfois, nous devons ajuster les facteurs pour obtenir la bonne réponse. Pour les fonctions composées, la dérivée est le sens contraire de la primitive, ce qui facilite l'identification des primitifs.
La constante multiplicative n'est pas un problème, car nous pouvons la trouver en effectuant une simple décomposition. Enfin, pour déterminer les primitives d'une fonction donnée, il est nécessaire de faire des calculs pratiques.
Dans l'exemple donné, nous devons déterminer toutes les primitives de la fonction exponentielle de U. Nous remarquons que la dérivée de la fonction interne est 6x, donc nous ajoutons le 6 pour obtenir la forme attendue U'. Ainsi, les primitives de la fonction sont de la forme E de 3x² plus 5, plus une constante.
En conclusion, pour trouver une primitive d'une fonction composée, il est essentiel de reconnaître les formes courantes et de vérifier nos calculs en dérivant la proposition de primitive.
Révisions Maths lycée
Analyse Terminale
ECG
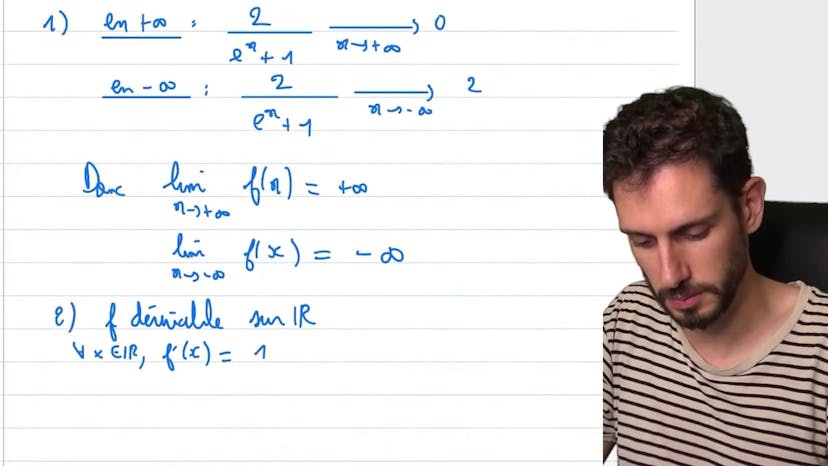
Primitive et réécriture
Ce cours présente une fonction définie par f2x égale x plus log de 4 plus 2 sur e2x plus 1. L'objectif est de chercher une primitive de cette fonction en deux parties.
Dans la première partie, on analyse la fonction et on cherche des expressions de primitives faciles à détecter. On commence par calculer la limite de f2x lorsque x tend vers plus l'infini et moins l'infini. La limite en plus l'infini est 0 et la limite en moins l'infini est 2. En étudiant le sens de variation de f, on déduit que la fonction est dérivable sur R et que la dérivée de f2x est toujours positive. En utilisant cette information, on conclut que la fonction f est croissante sur R.
Dans la deuxième partie, on trouve l'ensemble des primitives de f2x. On observe que f2x peut s'écrire comme x plus 2 plus log de 4. On intègre cette expression en utilisant les règles de base de l'intégration et obtient x² sur 2 plus 2x plus le logarithme de e2x plus 1 plus K, où K est une constante réelle.
En résumé, la fonction f2x égale x plus log de 4 plus 2 sur e2x plus 1 a comme primitives possibles x² sur 2 plus 2x plus le logarithme de e2x plus 1 plus K, avec K appartenant à R.
Révisions Maths lycée
Analyse Terminale
ECG
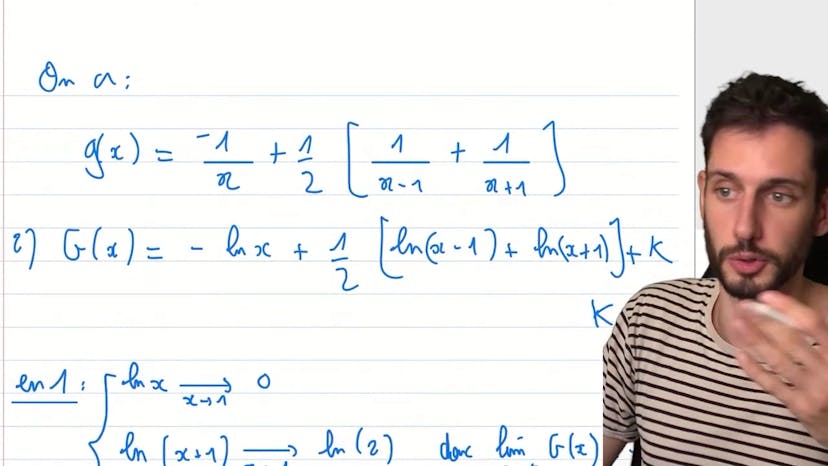
Décomposition en éléments simples
Dans ce cours, on apprend à simplifier des fractions rationnelles, c'est-à-dire des fractions avec des fonctions polynomiales. On peut séparer les monômes, qui sont des polynômes de degré 1. Pour simplifier ces fractions, on peut utiliser deux méthodes. La première consiste à mettre tous les termes au même dénominateur et les égaliser à 1. On identifie ensuite chaque terme et résout l'équation correspondante. Cependant, cette méthode est assez lourde. La deuxième méthode, plus astucieuse, consiste à prendre les expressions en x, x+1 et x-1 pour isoler les constantes a, b et c. On multiplie ces expressions à l'expression donnée pour obtenir des équations. En utilisant des valeurs appropriées pour x, on peut isoler chaque constante. Cette méthode est plus rapide et permet de résoudre le problème en deux minutes environ. Ensuite, on détermine les primitives. On ajoute une constante k et on précise que k est un nombre réel. Enfin, on étudie les limites de ces primitives en l'infini et en 1. On peut utiliser certaines propriétés du logarithme pour simplifier les expressions et calculer les limites. Par exemple, la limite du logarithme de x lorsque x tend vers 0 est égale à moins l'infini. En utilisant ces techniques, on peut déterminer les limites des primitives et résoudre l'exercice.
Révisions Maths lycée
Analyse Terminale
ECG

Polynôme × exponentielle
Lorsque nous avons une fonction exponentielle, la primitive sera probablement un polynôme du même degré multiplié par l'exponentielle. Par exemple, si nous avons une fonction de degré 2, la primitive sera probablement du type ax2 + bx + c * e^x. Pour trouver la dérivée de F' de moins 1, nous utilisons la propriété que la dérivée d'une fonction primitive est égale à la fonction elle-même. En utilisant les résultats de la question précédente, nous identifions les paramètres a et b et obtenons F' de x = -x + 3 - x^2 + 3x - 2x.


