 All subjects
All subjects
 All subjects
All subjects
Maths
Analyse
Première

Calcul d'expressions 1
Ce cours explique comment calculer les sinus et cosinus pour des expressions qui dépendent de n en utilisant le cercle trigonométrique. Le cercle trigo est une manière de voir les angles en associant un angle à la longueur de cercle qu'il peut parcourir. Les longueurs d'arc associées à un angle ont la même valeur de cosinus-sinus et peuvent être associées à une certaine valeur π ou un nombre de cercles en plus. Les valeurs de cosinus et sinus pour les expressions 2nπ, 2n+1π et nπ sont déduites. Le résultat pour nπ dépend de n, avec un sinus de 0 et un cosinus de -1 ou 1 si n est pair ou impair respectivement. Enfin, une expression complexe est simplifiée pour trouver le cosinus et le sinus pour le point correspondant. Il est important de retenir que moins 1 puissance n correspond à 1 si n est pair et à -1 si n est impair pour nπ.
Maths
Analyse
Première
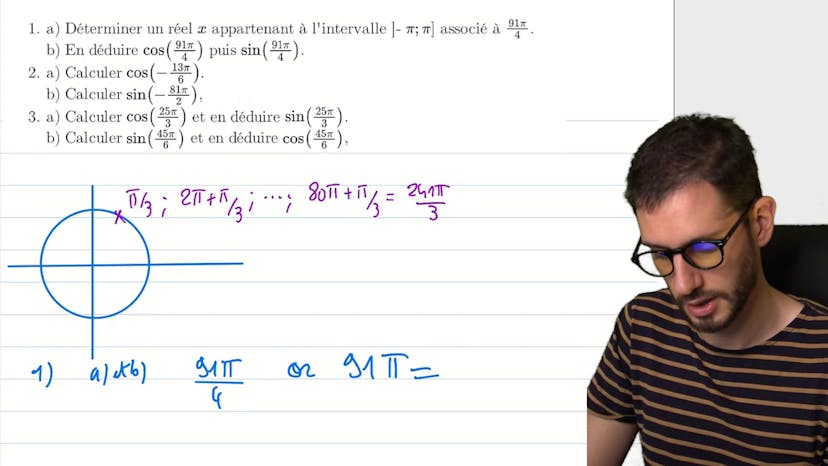
Calcul d'expressions 2
Apprendre les valeurs trigonométriques peut être simplifié en trouvant des valeurs équivalentes plus courantes. Par exemple, 241pi/3 peut être simplifié en pi/3 pour trouver les valeurs de cosinus et sinus. Pour trouver les valeurs pour 91pi/4, vous pouvez retirer des paquets de 2pi et exprimer 91pi/4 comme 10 paquets de 2pi plus 3pi/4. Les valeurs de cosinus et sinus pour 91pi/4 sont les mêmes que pour pi/4, mais avec des signes différents. Les questions 2a, b et 3a, b utilisent la même méthode.
Maths
Analyse
Première

Points sur le cercle trigo
Dans cet exercice sur le cercle trigonométrique, on doit placer des points astucieusement. Le point A associé au réel pi sur 3 est placé sur le cercle trigo. Ensuite, le point B symétrique de A par rapport à l'axe des abscisses est tracé. Les réels associés à ces points dans l'intervalle 0 de pi et dans l'intervalle moins pi pi sont demandés. Il y a une faute de français car ils veulent dire le réel associé à ce point dans chaque intervalle, pas les réels associés. Le nombre associé à A est pi sur 3, à B c'est 5 pi sur 3, et à C c'est 2 pi sur 3. Enfin, le point D symétrique de A par rapport à O est placé et le réel associé à ce point est 4 pi sur 3 entre 0 et 2 pi, et moins 2 pi sur 3 entre moins pi et pi. Il faut comprendre qu'on peut parcourir plusieurs tours et qu'un seul point du cercle peut représenter plusieurs nombres.
Maths
Analyse
Première
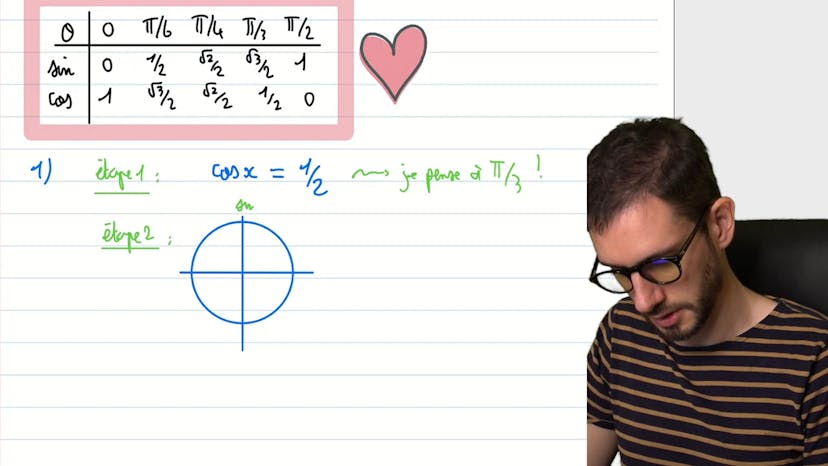
Equations trigos simples
La vidéo explique comment résoudre des équations trigonométriques simples en utilisant le cercle trigonométrique et le tableau des valeurs de sine et cosine. La première étape consiste à identifier la valeur classique à laquelle on peut se rapporter dans le problème. La deuxième étape consiste à tracer le cercle trigonométrique pour trouver les points où l'équation est vérifiée. Il est important de comprendre la contrainte de l'intervalle et de trouver les angles solutions dans cette plage. La vidéo illustre cet exemple pour résoudre 2cos(x) = 1 dans l'intervalle [0, 2π] avec les solutions x=π/3 et x=5π/3 et pour résoudre 2sin(x) = -1 avec les solutions x=7π/6 et x=11π/6 dans cet intervalle.
Maths
Analyse
Première

Inéquations trigos simples
Ce cours explique comment résoudre des inéquations en utilisant un tableau de valeurs de base. Le premier exemple montre comment réécrire une inéquation en utilisant le cosinus et la racine de 2. En traçant un cercle trigo et en utilisant le point pi sur 4, l'élève peut identifier les angles pour lesquels le cosinus est inférieur à pi sur 4, en excluant les points de l'axe des abscisses. L'ensemble des angles est entre moins pi et pi, en incluant moins pi sur 4 exclu et pi sur 4 exclu. Le deuxième exemple utilise la racine de 2 sinus x et se réécrit en utilisant la racine de 6, qui peut être simplifiée, et en utilisant le sinus. Le cercle trigo est tracé sur l'axe vertical, en utilisant le point pi sur 3. L'ensemble des angles avec un sinus supérieur à racine de 3 sur 2 est entre moins pi et pi et inclus pi sur 3 et 2 pi sur 3. En résumé, pour résoudre une inéquation, il faut transformer l'équation pour utiliser le tableau de valeurs, tracer un cercle trigo, puis lire les angles correspondants en parcourant l'ensemble donné.
Maths
Analyse
Première

Equation trigo où poser X=sinx
Dans ce cours, on apprend à résoudre une équation trigonométrique qui inclut cos et sin, ainsi que des termes cos² et sin². Pour simplifier l'équation, on utilise l'identité fondamentale de la trigonométrie pour remplacer cos² par 1-sin². Ensuite, on pose un grand X pour résoudre l'équation de degré 2 qui apparaît. Finalement, on revient à la trigonométrie pour trouver les solutions de l'équation d'origine en fonction de X. Les solutions en fonction de X forment un cercle trigo et l'ensemble des solutions réelles est obtenu en trouvant quand le sinus vaut 1.
Maths
Analyse
Première
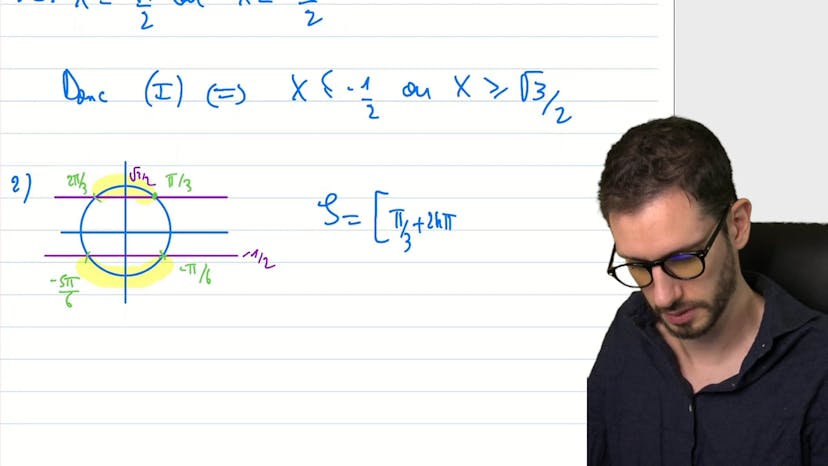
Inéquation trigo où poser X=sinx
Dans cette leçon de mathématiques, nous avons une équation avec seulement du sinus, donc pas besoin de faire un changement de variable. Nous résolvons l'équation en posant "X = sin(x)" et en trouvant les racines à partir de cela. Ensuite, nous utilisons une astuce pour résoudre l'inéquation qui nous est donnée. Nous rappelons également la méthode X2-XS+P pour trouver les racines d'une équation à deux degrés. Finalement, nous utilisons une méthode trigo pour trouver l'ensemble des solutions.
Maths
Analyse
Première

Etude de fonction trigo 1
Dans cet exercice, on étudie une fonction qui dépend de x et qui contient du cos et du sin. On commence par analyser les valeurs de la fonction à deux points spécifiques. Ensuite, on découvre les propriétés de la fonction et détermine si elle est impaire ou périodique. Finalement, on effectue une étude de fonctions en utilisant la dérivée. On résout une équation pour identifier les variations de la fonction et trouver ses maximums et minimums. En résumé, cet exercice est un exercice d'analyse de fonctions qui utilise des propriétés de trigonométrie et de symétrie pour déterminer les caractéristiques de la fonction.
Maths
Analyse
Première

Etude de fonction trigo 2
Ce cours porte sur l'étude de la fonction f(x) = -cosine(3x)/3. Tout d'abord, la fonction parité de f est démontrée, car elle est paire pour tout x. Ensuite, il est montré que f est périodique, avec une période de 2pi. Il est recommandé d'étudier la fonction sur l'intervalle [-pi, pi] à cause de sa parité et de sa périodicité. Le signe de f'(x) est ensuite étudié et il est montré que f(x) est toujours positif ou nul sur l'intervalle [0, 2pi]. Finalement, un tableau de variation de la fonction sur [-pi, pi] est dressé en utilisant sa parité et sa périodicité. Le même tableau est étendu sur [-3pi, pi] en utilisant la même méthode.
Maths
Analyse
Première

Etude de fonction trigo 3
Ce cours traite de l'étude des variations de la fonction exponentielle de cos x. On commence par montrer que f est une fonction paire et symétrique. On explique ensuite comment interpréter graphiquement f sur un intervalle de taille de pi en utilisant la périodicité de la fonction. On donne la dérivée de f et on montre que f' est négative sur l'intervalle de 0 à pi, ce qui implique que f décroît sur cet intervalle. En déduisant les extrémums de f sur l'intervalle de moins pi à pi, on trouve un maximum en 0 et des minimums en moins pi et pi. En suivant le tableau de variations de f, on peut tracer la fonction sur moins 2 pi à 3 pi, qui monte et descend périodiquement.
Maths
Analyse
Première

Equations trigos : ensembles de résolution
Ce cours traite de la résolution d'équations trigonométriques plus complexes que celles habituellement enseignées. Il met l'accent sur la résolution dans un intervalle spécifique et présente un théorème qui permet de trouver deux solutions possibles à une équation comportant le sinus d'un angle connu. L'exemple donné montre comment trouver quatre solutions possibles pour une telle équation dans l'intervalle entre moins 2 pi et 2 pi. La méthode consiste à tester différentes valeurs de k pour déterminer les solutions valables dans l'intervalle donné.
Maths
Analyse
Première
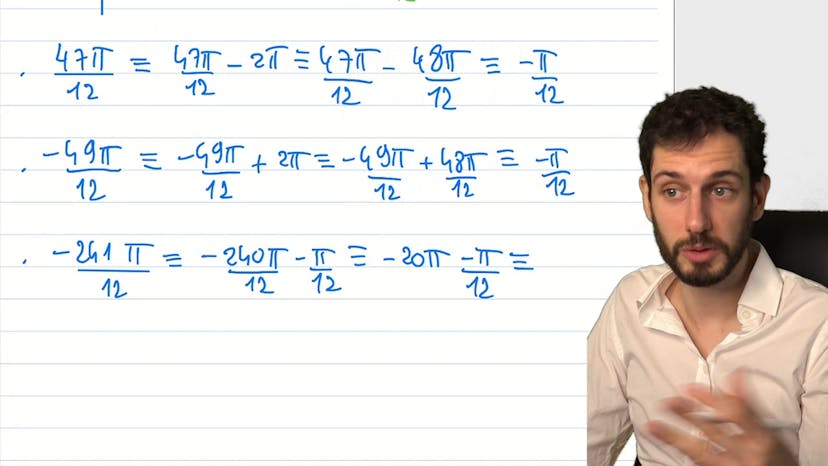
Point 1 : Mêmes mesures sur le cercle trigo
Le cours explique comment fonctionne le placement des angles sur le cercle trigonométrique. Chaque point du cercle correspond à plusieurs valeurs de longueur d'arc de cercle. Il est alors possible d'enlever des paquets de 2pi pour retrouver la mesure fondamentale ou la plus petite. Le cours présente plusieurs exemples pour aider à comprendre le concept et invite les étudiants à s'entraîner à enlever ces paquets pour retrouver la mesure souhaitée.
Maths
Analyse
Première

Point 2 : Calcul de certains sin et cos grâce au cercle
Ce cours explique comment connaître les valeurs de pi sur 6, pi sur 3, pi sur 4, pi sur 2 en utilisant les valeurs de sine et de cos, et comment trouver des valeurs approchantes en utilisant des symétries sur le cercle. Il est important de mémoriser les valeurs canoniques de sine et de cos pour les utiliser efficacement. Cette méthode est simple et efficace pour lire les angles et éviter d'apprendre des centaines de valeurs.
Maths
Analyse
Première
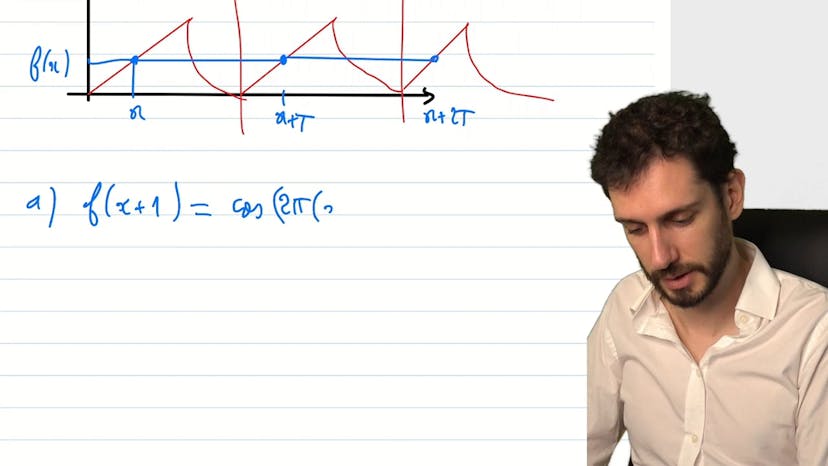
Point 3 : les fonctions périodiques
Une fonction périodique se caractérise par la répétition d'un motif de taille fixe appelé la période. Mathématiquement, cela signifie que pour tout nombre de périodes ajoutées, la valeur de la fonction reste la même. Pour vérifier qu'une fonction est périodique, il suffit de vérifier que f(x+T) = f(x) pour une période T donnée. Les fonctions sinus et cosinus sont périodiques de période 2π, ce qui permet de résoudre certains exemples en trouvant une période commune.
Maths
Analyse
Première

Somme de sin et cos
Ce cours aborde les exercices de mathématiques qui impliquent des sommes de sinus et de cosinus. En utilisant un cercle trigo, les valeurs des angles sont placées et les valeurs des sinus et cosinus associées peuvent être extraites rapidement. Dans l'un des exemples, les valeurs s'annulent et il ne reste que 0. Pour résoudre certains problèmes, il est important de connaître les valeurs clés de sinus et de cosinus, comme celles pour π sur 6, π sur 4, π sur 3, π sur 2, et 0. Les angles sont également présentés comme demi-racines successives dans l'ordre de leur valeur croissante. En utilisant ces connaissances sur les valeurs clés et le cercle trigo, le cours montre comment résoudre efficacement l'exercice.
Maths
Analyse
Première

Petit problème cercle trigo
Dans cet exercice de trigonométrie, on doit trouver les coordonnées de quatre points d'un carré à partir d'un point donné. Le premier point est donné par ses coordonnées, qui sont liées à la trigo, et se trouve sur le cercle de rayon 1 de centre haut, associé à l'angle pi sur 4. En utilisant la définition géométrique du carré, on peut trouver les coordonnées des autres points en observant que les diagonales se coupent en leur milieu, sont perpendiculaires et ont une même longueur. Pour trouver les coordonnées des points B et D, on ajoute plus pi sur 2 au premier angle, pour obtenir des angles de 3pi sur 4 et 7pi sur 4 respectivement. On peut ensuite lire facilement les coordonnées de ces points sur le cercle trigo en utilisant les valeurs du sinus et du cosinus. En utilisant la caractérisation du carré par ses diagonales, on peut trouver les coordonnées de tous les points du carré.
Maths
Analyse
Première

Exo bilan sur les changements de variable X=...
Dans cet exercice, on utilise une fonction contenant uniquement la variable inconnue X en termes de causes. Pour résoudre l'équation, on utilise un changement de variable en remplaçant X par X² et X. On résout ensuite les racines X1 et X2 et on les compare à la contrainte de l'intervalle de X entre -1 et 1. Ensuite, on résout F2X égale à 0 en utilisant les valeurs de X1 et X2, qui sont ensuite comparées à un deuxième inéquation pour obtenir la réponse finale.
Maths
Analyse
Première
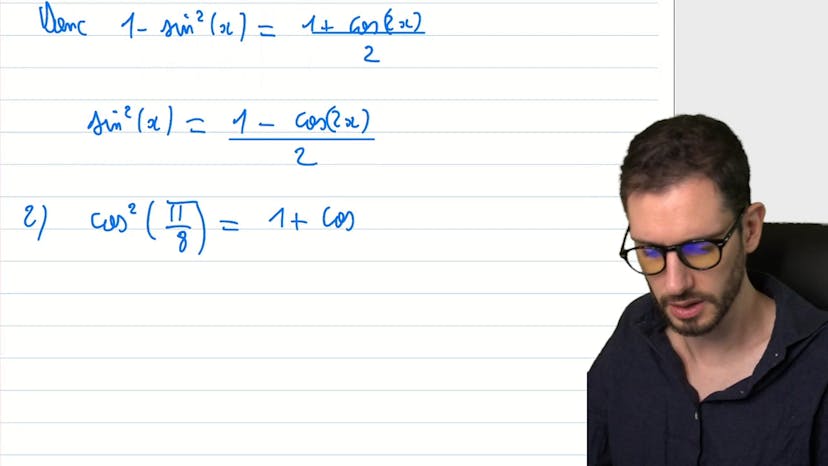
Valeur particulière d'un cos
Ce cours explique comment trouver la valeur de cos ou sin d'un réel donné en utilisant une formule admise. Pour trouver sin²x en fonction de cos²x, on utilise l'identité fondamentale de l'intrigo, sin²x + cos²x = 1. Pour trouver cosinus et sinus de pi sur 8, on utilise la formule cos²x = 1 + cos2x le tout sur 2. Ensuite, il est important de justifier pourquoi la solution positive est la bonne. En effet, pour pi sur 8, le cosinus et le sinus doivent être positifs car l'angle est compris entre 0 et pi sur 2. Enfin, il est recommandé de poser des questions dans le forum si besoin.


