 All subjects
All subjects
 All subjects
All subjects
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Intro Suites et limites
Dans cette vidéo, on aborde le sujet des limites de suite. Une limite de suite est lorsque les valeurs d'une suite tendent vers une valeur spécifique. Un exemple est donné où une suite augmente et finit par se stabiliser autour d'une certaine valeur, ce qui suggère qu'elle tend vers une limite. Cependant, les mathématiciens préfèrent des définitions formelles qui peuvent sembler complexes, mais l'objectif est de les rendre plus accessibles en se référant aux graphiques correspondants.
On compare ensuite ce sujet à l'étude de la dérivée en mathématiques, où au début, on utilise des définitions formelles puis on utilise des tables de dérivées classiques pour simplifier le processus. De la même manière, pour les limites de suite, il y a des définitions formelles à connaître, mais aussi des tableaux de limites classiques qui seront utiles.
Le cours se divise en trois parties principales. La première porte sur la définition de la limite pour l'infini positif, l'infini négatif et une valeur réelle spécifique. On aborde également la propriété d'unicité de la limite. La deuxième partie concerne les limites de référence et les opérations possibles sur les limites. Des tableaux de limites classiques sont présentés. Enfin, la troisième partie aborde les limites des suites géométriques, avec un rappel sur la somme des termes d'une suite géométrique et les cas où cette somme peut avoir une limite.
Quatre principales méthodes sont présentées. La première consiste à appliquer la définition formelle des limites dans certains exercices. Les deuxième et troisième méthodes sont basées sur les limites de référence et les opérations sur les limites, qui permettent de prédire certaines limites ou de résoudre les cas plus complexes. Enfin, une méthode rappelant la somme des termes d'une suite géométrique est également abordée.
La vidéo se termine en encourageant les spectateurs à poser des questions dans la FAQ et en annonçant une prochaine vidéo sur le sujet.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Limite finie
Dans cette première vidéo sur les limites en mathématiques, nous allons aborder la notion de limite réelle. La limite réelle correspond à la valeur vers laquelle une suite converge intuitivement lorsque n augmente. Pour une meilleure précision, nous utilisons la notion de couloir en mathématiques. Dans cette vidéo, nous allons donc expliciter l'idée de couloir autour de la limite et montrer que la convergence peut se faire de manière progressive (croissante ou décroissante) mais aussi de manière plus chaotique.
La définition officielle de la limite nous dit que si une suite UN converge vers un réel L, alors tous les termes de la suite seront inclus dans n'importe quel intervalle autour de L à un certain moment. Pour mieux comprendre cette définition, nous allons utiliser un graphique. Nous prenons une suite et nous choisissons un intervalle autour de la limite supposée. Si, à partir d'un certain moment, tous les termes de la suite sont inclus dans cet intervalle, alors nous pouvons dire que la limite est correcte. En d'autres termes, plus nous réduisons la taille de l'intervalle, plus les termes de la suite convergent vers la limite choisie.
Nous pouvons illustrer cela avec différents exemples de suites convergentes. Nous pouvons prendre une suite croissante, une suite décroissante ou même une suite oscillante. Dans tous les cas, si tous les termes de la suite sont inclus dans un intervalle autour de la limite, alors nous pouvons dire que la limite est correcte.
En conclusion, dans cette première vidéo, nous avons expliqué la notion de limite réelle en utilisant la notion de couloir. Nous avons montré que la convergence peut se faire de différentes manières (croissante, décroissante ou oscillante) tant que tous les termes de la suite sont inclus dans un intervalle autour de la limite. Dans la prochaine vidéo, nous approfondirons davantage ces notions. N'hésitez pas à poser vos questions dans la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

En l'infini
Dans cette vidéo, l'enseignant aborde la notion de limite infinie. Il explique que lorsqu'une suite tend vers l'infini, cela signifie que pour n'importe quelle valeur seuil, il est possible de trouver un rang à partir duquel tous les termes de la suite seront supérieurs à cette valeur seuil. Il illustre cette notion avec un graphique représentant une suite croissante basée sur la parabole x^2. Il montre que peu importe la valeur seuil choisie, il existe un rang à partir duquel tous les termes de la suite sont supérieurs à cette valeur. Il mentionne également que la notion de limite infinie est symétrique, c'est-à-dire qu'une suite tend vers moins l'infini si tous ses termes sont inférieurs à n'importe quelle valeur seuil négative. Il propose également de poser des questions dans la FAQ si besoin et annonce la prochaine vidéo. Ce résumé met l'accent sur les notions clés du cours, en utilisant des phrases simples et courtes pour optimiser la convivialité du référencement.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
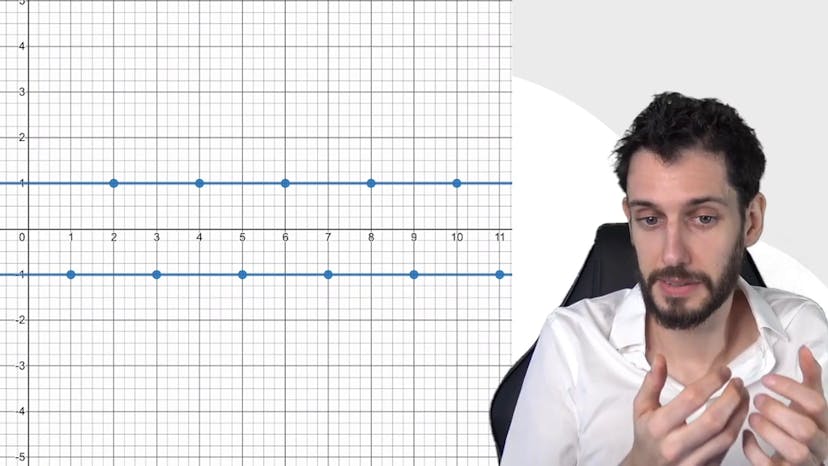
Unicité et Divergence
Dans cette vidéo, nous approfondissons notre compréhension de la convergence et des limites dans le contexte des suites.
Le premier point important est que lorsque nous avons une limite finie, elle est unique. En d'autres termes, si nous nous approchons d'une valeur, nous ne pouvons nous approcher que d'une seule valeur. Cela est intuitif et facile à comprendre.
Le deuxième point concerne le vocabulaire. Nous utilisons le terme "convergence" pour décrire une suite lorsque nous avons une limite finie. Cependant, il est crucial de comprendre que ne pas converger ne signifie pas automatiquement tendre vers l'infini positif ou négatif. Il est possible de ne pas converger différemment.
Il existe un cas spécifique de divergence appelé "oscillation". Par exemple, prenons la suite (-1) élevé à la puissance n. Elle vaut 1 lorsque n est égal à 0, -1 lorsque n est égal à 1, 1 lorsque n est égal à 2, et ainsi de suite. Cette suite oscille entre -1 et 1, donc elle ne converge ni vers -1 ni vers 1, et n'a pas de limite finie. Cependant, elle ne tend pas non plus vers l'infini positif ou négatif. Elle présente simplement un comportement d'oscillation permanent.
Il est important de mentionner que l'existence de petites convergences pour certains termes de la suite ne signifie pas une convergence globale de toute la suite. C'est un concept plus avancé qui va au-delà du programme scolaire et implique l'extraction de sous-suites à partir de suites plus générales. Dans l'exemple précédent, on pourrait extraire les termes "en haut" de la suite et dire qu'ils tendent vers 1. Cependant, pour la suite dans son ensemble, il n'y a pas de limite, pas de tendance vers l'infini positif ou négatif.
Ainsi, nous avons exploré différentes possibilités de convergence et de divergence des suites. Si vous souhaitez plus de détails ou des informations supplémentaires, n'hésitez pas à consulter notre FAQ ou à nous contacter. À bientôt !
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Limites de référence et opérations
Dans ce cours, nous avons étudié les limites de suites et avons appris quelques outils pratiques qu'il est important de connaître dans le programme de mathématiques.
Tout d'abord, nous avons vu que les puissances de n tendent vers plus l'infini lorsque n tend vers plus l'infini. Cela s'applique non seulement aux puissances entières de n, mais aussi aux racines de n. Ainsi, on peut dire que les puissances positives de n, quel que soit l'entier k ou le nombre rationnel, tendent vers plus l'infini. De plus, il est important de noter que plus la puissance augmente, plus la suite tend vers plus l'infini rapidement. Par exemple, n³ croît plus rapidement que n².
Ensuite, nous avons abordé les puissances négatives de n, c'est-à-dire 1/n. Dans ce cas, la suite tend vers zéro, car 1 divisé par un nombre très grand devient très petit. Ainsi, toutes ces fonctions tendent vers 0.
Nous avons également étudié comment gérer les opérations sur différentes suites. Par exemple, si nous connaissons les limites de deux suites, pouvons-nous en déduire la limite de leur somme ? Dans la plupart des cas, la réponse est oui. En effet, si une suite tend vers l et une autre tend vers l', alors leur somme tend vers l + l'. Si l'une tend vers plus ou moins l'infini et l'autre vers une limite finie, c'est l'infini qui l'emporte. De même, si les deux tendent vers plus ou moins l'infini, le résultat sera également plus ou moins l'infini. Cependant, lorsque la limite est une forme indéterminée, il n'y a pas de règle prédéterminée à suivre. Il faut donc évaluer chaque cas individuellement.
Enfin, nous avons mentionné deux autres formes indéterminées à connaître : le produit de deux suites, où l'une tend vers zéro et l'autre vers l'infini, ainsi que le quotient de deux suites, où l'une tend vers l'infini et l'autre vers zéro. Il est important de reconnaître ces formes indéterminées car elles nécessitent une méthode spécifique pour les résoudre.
En conclusion, il est essentiel d'apprendre et de mémoriser les tables des limites des suites, ainsi que de comprendre les quatre formes indéterminées mentionnées : plus l'infini, moins l'infini, zéro fois plus l'infini et zéro fois l'infini en négatif, et le quotient de l'infini sur l'infini ou le quotient de zéro sur zéro. En connaissant ces concepts, vous serez prêt à résoudre des exercices sur les limites de suites.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
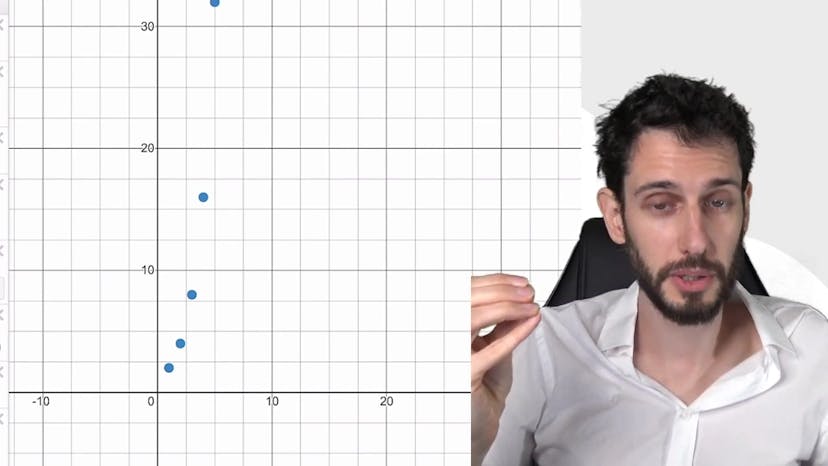
Suites géométriques - illustration
Ce cours explique les différents comportements des suites géométriques en fonction de la valeur de la raison, Q. Lorsque Q est plus grand que 1, la suite converge vers l'infini. Par exemple, si Q équivaut à 3, la suite augmente de plus en plus avec chaque terme. Ce comportement peut être démontré à l'aide de l'inégalité de Bernoulli.
Lorsque Q est compris entre -1 et 1, la suite converge vers 0. Par exemple, si Q équivaut à 0,5, chaque terme devient de plus en plus petit, et à l'infini, il reste seulement 0. Ce comportement s'explique par le fait que chaque terme est une fraction de plus en plus petite du terme précédent.
Si Q équivaut à 1, la suite converge simplement vers 1, ce qui est un cas trivial.
En revanche, lorsque Q est inférieur à -1, la suite diverge, mais d'une manière plus complexe. Elle oscille autour de 0 en s'écartant tantôt vers le positif, tantôt vers le négatif. Ce comportement est illustré graphiquement en montrant les termes successifs de la suite.
Pour résumer, lorsque la raison est proche de 0, la suite converge progressivement vers 0, que ce soit de manière oscillante ou non. Lorsque la raison est plus grande que 1 ou plus petite que -1, la suite s'écarte de 0, soit vers l'infini, soit de manière plus complexe.
Ce cours prépare à une prochaine vidéo qui démontrera ces comportements.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Suites géométriques : démo
Dans cette vidéo, nous démontrons les intuitions graphiques sur la limite des suites géométriques. Il y a plusieurs cas à démontrer. Dans le premier cas, lorsque Q est strictement supérieur à 1, nous démontrons que Q élevé à la puissance n tend vers l'infini. Pour cela, nous utilisons l'inégalité de Bernoulli et le terrain de comparaison. En posant Q = 1+h, avec h positif, nous appliquons l'inégalité de Bernoulli pour écrire que 1+h élevé à la puissance n est supérieur ou égal à 1+nh. Comme 1+nh est une suite arithmétique de raison positive qui tend vers l'infini, le terrain de comparaison nous permet d'affirmer que Q élevé à la puissance n tend vers l'infini. Les autres cas se rapportent au cas précédent. Par exemple, lorsque Q est entre 0 et 1, nous posons P = 1/Q et utilisons le résultat précédent pour dire que P élevé à la puissance n tend vers l'infini. Il en découle que Q élevé à la puissance n tend vers 0. Dans le dernier cas, nous appliquons le théorème des gendarmes pour encadrer la suite Q élevé à la puissance n entre deux suites qui convergent vers 0. Ainsi, Q élevé à la puissance n tend également vers 0. Les deux autres cas sont de simples astuces pour éviter de faire trop d'efforts lors de la démonstration. La démonstration des trois formules est assez rapide, avec un cas particulièrement fort lorsque Q est plus grand que 1. Les deux autres cas sont des façon astucieuses de réutiliser des résultats précédents. Cette démonstration doit être connue par cœur dans le programme. N'hésitez pas à poser vos questions dans la FAQ et je vous retrouve dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Limite avec A ou Ɛ
Dans ce cours, nous allons aborder la définition formelle d'une limite, ce qui peut être déroutant pour les élèves, mais essentiel pour ceux qui poursuivent leurs études en mathématiques. Nous allons utiliser des exemples pour expliquer comment comprendre la définition d'une limite avec les epsilon.
La suite Un est définie comme égale à 3n + 2. Nous voulons montrer que, pour tout réel A strictement supérieur à 0, il existe un entier naturel n0 tel que si n est supérieur à n0, alors Un est supérieur à A.
En d'autres termes, peu importe à quel point A est grand, nous voulons montrer qu'à partir d'un certain rang n0, tous les termes de la suite sont supérieurs à cette barrière A.
Si nous prenons A comme étant aussi grand que nous le souhaitons, y compris des valeurs très élevées, cela revient à définir une limite à l'infini.
Nous résolvons l'équation 3n + 2 > A, ce qui nous donne n > (A - 2) / 3.
Mais n doit être un entier naturel, donc nous ne pouvons pas dire que n0 est égal à cette expression.
Pour montrer l'existence d'un entier n0, nous prenons la partie entière de (A - 2) / 3 + 1 comme valeur de n0.
Ainsi, si n est supérieur à la partie entière de (A - 2) / 3 + 1, alors n sera également supérieur à (A - 2) / 3, ce qui signifie que Un sera supérieur à A.
Cela correspond à la définition formelle de la limite à l'infini. Nous pouvons imaginer une barrière A1, A2, A3, etc., et il existera toujours un rang à partir duquel tous les termes de la suite seront au-dessus de cette barrière.
Bien que les définitions formelles puissent sembler compliquées au départ, elles deviennent plus claires avec la pratique. Si vous avez des questions, consultez la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Forme indéterminée 1 : factoriser par terme de plus haut degré
Dans cette leçon, nous étudions les différentes formes indéterminées pour le calcul de limites et comment les résoudre. Nous commençons par l'exemple d'un polynôme en n. La règle est que seul le terme de plus haut degré compte et prédomine. Pour démontrer cela rigoureusement, nous factorisons par le terme de plus haut degré. Dans cet exemple, le polynôme est n²-n. En factorisant par n², on obtient 1 + 1/n. Comme 1/n tend vers 0, on n'a plus de forme indéterminée et le résultat est donc l'infini. Cette règle s'applique à tous les polynômes, où le coefficient devant le terme de plus haut degré détermine le résultat. Dans ce cas, le coefficient est 1, donc le résultat est plus infini. Cela concerne les limites lorsque n tend vers plus infini.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Forme indéterminée 2 : la quantité conjuguée
Ce cours porte sur les méthodes de calcul pour les fonctions rationnelles, c'est-à-dire les polynômes divisés par d'autres polynômes. La technique utilisée est la même que pour les polynômes, on factorise par le terme de plus haut degré. Par exemple, si nous avons la suite Vn égale à 4n² sur n plus 1, nous identifions le terme de plus haut degré (2), et donc nous factorisons par n² en haut et par n en bas. Les n se simplifient et nous obtenons 4n au numérateur divisé par 1 plus 1 sur n qui tend vers 1. Ainsi, nous levons l'indétermination et constatons que par quotient, Vn tend vers plus infini.
En outre, il existe trois cas possibles pour les fonctions rationnelles. Si le degré du polynôme au numérateur est strictement supérieur au degré du polynôme au dénominateur, celui-ci l'emporte et la limite tend vers plus infini. Si le degré du dénominateur est strictement supérieur au degré du numérateur, le dénominateur l'emporte et la limite tend vers 0. Si les degrés des polynômes au numérateur et au dénominateur sont égaux, la limite tend vers le rapport des coefficients dominants des deux polynômes.
Par exemple, si nous prenons la suite Un égale à 3n² plus 2n plus 1 sur 4n² plus n plus 4, nous factorisons par le terme de plus haut degré (n²) en haut et en bas, ce qui nous donne 3 plus 2n plus 1 sur n² au numérateur, et 4 plus 1 sur n plus 4 sur n² au dénominateur. Finalement, la limite tend vers 3 quarts, le rapport des coefficients dominants.
En conclusion, dès qu'il s'agit d'une fonction rationnelle, nous nous trouvons systématiquement dans l'un de ces trois cas.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Limite d'une somme géométrique
En terminale, lorsqu'on a une limite à calculer, il n'est pas nécessaire d'utiliser plusieurs méthodes. On doit d'abord vérifier si les termes de la somme correspondent à une suite arithmétique ou une suite géométrique. Si ce n'est pas le cas, cela nécessite une étude précise.
Dans cet exemple, les termes de la somme sont les termes consécutifs d'une suite géométrique. On identifie donc la formule correspondante, qui est u0 * q^n, avec u0 = 1 et q = 3.
Pour s'assurer de ne pas se tromper sur le nombre de termes, il est important de vérifier si l'expression est cohérente. Dans ce cas, on a vérifié que u0 = 1 et u1 = 3, ce qui est correct.
En utilisant la formule générale, la somme s'exprime comme u0 * (1 - q^(n+1))/(1 - q). Il faut bien se rappeler que le nombre de termes est n+1, car il faut inclure le terme u0.
On peut simplifier cette expression en utilisant les limites usuelles. On sait que q^n tend vers l'infini lorsque la valeur absolue de q est supérieure à 1. Par conséquent, la somme tend également vers l'infini.
En conclusion, la somme de ces termes consécutifs de la suite géométrique tend vers l'infini.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Trouver à la calculette "le plus petit entier tel que..."
Dans ce cours, nous étudions une suite et cherchons à trouver le plus petit entier qui dépasse une certaine valeur. La suite est définie par u0 = 2 et la relation de récurrence un+1 = 3un. En observant cette relation, on peut voir que la suite augmente rapidement en multipliant chaque terme par 3. Ainsi, en partant d'une valeur positive, on se rend compte que la suite tend vers l'infini.
En utilisant un petit programme, nous pouvons trouver le plus petit entier naturel tel que un > 1000. Le programme utilise une boucle while tant que un est inférieur à 1000. À chaque itération, un prend la valeur de 3un, et n est incrémenté de 1 pour compter le nombre d'opérations. À la fin, le programme affiche la valeur de n pour indiquer le rang de la suite.
Il est également possible de trouver cette valeur par itération sans l'aide d'un programme. En multipliant successivement par 3, on peut voir que u3 = 54, u4 = 162, u5 = 486, et u6 = 1458. Ainsi, le premier entier tel que un > 1000 est 6.
Il est important de bien comprendre le rôle de chaque élément du programme et les objectifs de l'exercice. Si des questions subsistent, il est possible de consulter la FAQ pour plus d'informations.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
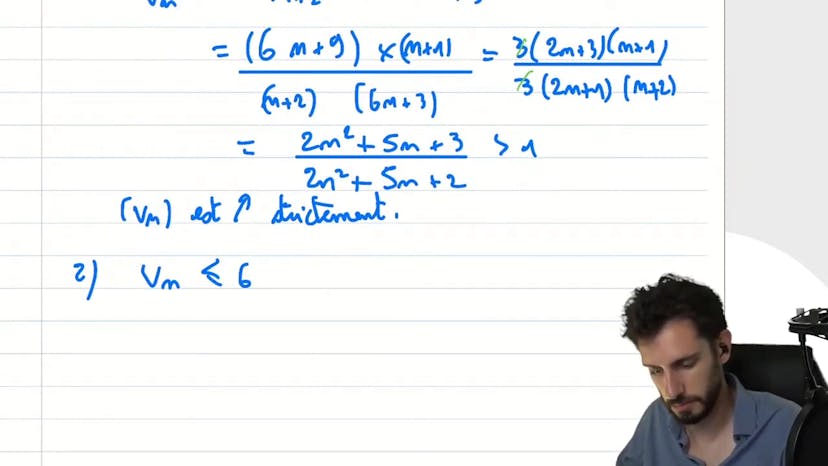
Suite-fraction
La première méthode consiste à étudier les variations de la suite vn = 6n + 3 / (n + 1). On utilise le critère de croissance en calculant le ratio vn+1 / vn et on trouve que ce ratio est strictement supérieur à 1. Donc la suite vn est strictement croissante.
Ensuite, on montre que la suite est majorée par 6 en utilisant le fait que vn + tigre = 6 si et seulement si 6n + 3 + tigre = 6, ce qui est vrai lorsque tigre = 6 - 3. Donc vn + tigre = 6.
Enfin, en utilisant le théorème de convergence monotone, on conclut que la suite vn converge.
Dans la deuxième méthode, on écrit vn sous une autre forme en utilisant le fait que vn = 6n + 3 / (n + 1) = (6(n + 1) - 3) / (n + 1). On sépare la fraction en deux et on obtient une fonction f(n) = 6 - 3 / (n + 1), qui est une fonction hyperbole décroissante.
Comme f est décroissante sur R+, on en déduit que la suite vn est croissante. De plus, on remarque que 6 - 3 / (n + 1) est égal à 6 pour tout n entier. Donc la suite vn est majorée par 6.
Enfin, on utilise la limite classique de 3 / (n + 1) qui tend vers 0 lorsque n tend vers l'infini. Donc la limite de vn est 6.
En résumé, la suite vn = 6n + 3 / (n + 1) est une suite croissante majorée par 6 et elle converge vers 6.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Plein de limites !
Ce cours traite de différentes méthodes de gestion des limites. Deux méthodes principales sont présentées : la méthode du terme dominant et la méthode de l'encadrement.
La méthode du terme dominant consiste à comparer les termes dominants en haut et en bas d'une fraction pour déterminer le comportement de la suite. On peut factoriser en haut et en bas par le terme dominant, ce qui permet de conclure que la suite tend vers 0.
La méthode de l'encadrement est utilisée dans le cas où la question concerne les limites d'une suite avec des puissances négatives et des fonctions trigonométriques. Il suffit d'encadrer ces termes entre -1 et 1 et d'appliquer un théorème d'encadrement pour obtenir la limite de la suite.
D'autres exemples de limites de suites sont également étudiés, tels que les suites qui tendent vers l'infini ou vers des limites finies. Dans ces cas, il est souvent nécessaire d'utiliser le théorème de comparaison ou le théorème des gendarmes pour déterminer la limite de la suite.
En résumé, ces méthodes permettent de déterminer les limites de suites de manière efficace et rapide. Il est également recommandé d'utiliser l'encadrement lorsque les termes de la suite sont des puissances négatives, des sinus ou des cosinus.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Téléscopage !
Le cours aborde la notion de limites de suites définies comme des sommes de termes d'autres suites.
Dans un premier temps, il faut déterminer la limite de la suite Un, qui est égale à 1/n. On obtient que Un tend vers 0.
Ensuite, il est demandé de montrer que pour toute valeur de n, Un est égale à 1/n - 1/(n+1). Il est conseillé de prendre la manière la plus simple pour démontrer cette équivalence, en partant de 1/n - 1/(n+1) et en simplifiant jusqu'à obtenir Un.
En utilisant la question précédente, on peut ensuite calculer la somme Sn de la suite Un. En utilisant la version de Un obtenue précédemment, on obtient une somme télescopique, où les termes se simplifient les uns les autres. La somme Sn converge alors vers 1.
En déduisant la limite de Sn lorsque n tend vers l'infini, on obtient que cette limite converge vers 1.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
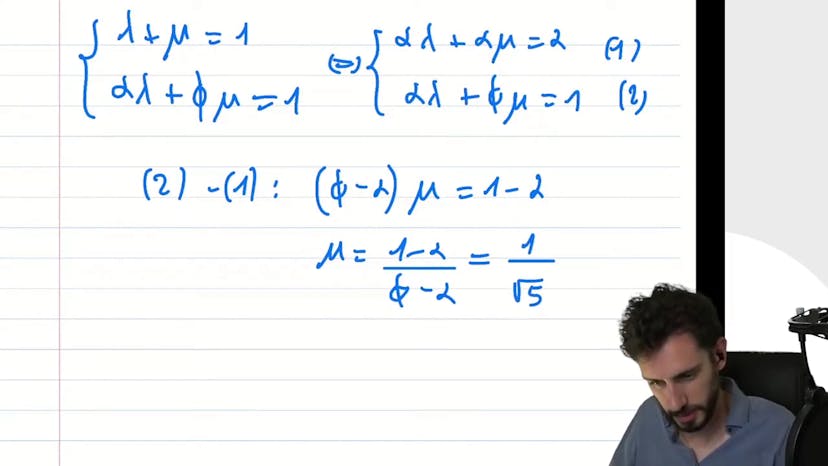
Prépa : Fibonacci
La suite de Fibonacci et le nombre d'or sont définis par une relation de récurrence où chaque terme est la somme des deux précédents. Pour calculer les termes de la suite, il faut connaître les deux premiers termes (u0 et u1).
On cherche ensuite à trouver des réels (a, b, lambda, mu) tels que chaque terme puisse être exprimé sous forme d'une combinaison linéaire de sommes géométriques.
Plutôt que de chercher à résoudre les équations directement, on peut analyser cette relation en se demandant s'il existe une seule somme géométrique qui pourrait vérifier cette relation, puis vérifier s'il y en a plus.
En utilisant cette approche, on trouve que les valeurs possibles pour a et b sont les suivantes : a = (1 + √5)/2 (le nombre d'or) et b = (1 - √5)/2.
En utilisant ces valeurs, on peut résoudre les 2 équations avec les 2 inconnus lambda et mu et trouver leurs valeurs respectives.
Ainsi, on obtient les valeurs exactes pour les termes de la suite de Fibonacci.
En résumé, la suite de Fibonacci peut être exprimée sous forme de sommes géométriques en utilisant les valeurs a et b (lesquelles sont calculées à partir du nombre d'or), et les constantes lambda et mu sont déterminées par les équations provenant des conditions initiales de la suite.
Révisions Maths lycée
Analyse Terminale
BCPST

Intro Suites et limites
Dans cette vidéo, nous abordons les limites de suite mathématique. Une suite est considérée comme ayant une limite lorsque ses valeurs tendent à se rapprocher d'une certaine valeur fixe à mesure que l'indice de la suite augmente. Dans l'exemple donné, une suite est tracée avec un graphique montrant comment les valeurs se rapprochent progressivement d'une valeur "plateau" à mesure que l'indice augmente. Cependant, pour être précis en mathématiques, nous devrons utiliser des définitions formelles, qui peuvent sembler complexes et effrayantes au début. Le professeur promet de nous familiariser et de traduire ces définitions, en mettant toujours l'accent sur les graphiques pour illustrer les concepts. Il compare également ce processus à l'étude de la dérivée en première année, où nous avons d'abord appris une définition complexe avant de passer à des tables de dérivées classiques pour faciliter les calculs. De même, pour les limites de suite, nous aurons des définitions formelles, mais nous aurons également des tableaux de limites classiques à apprendre. Les principaux points du cours seront les définitions des limites tendant vers l'infini, moins l'infini et une valeur réelle fixe, ainsi que la propriété d'unicité des limites. Il y aura aussi une partie sur les limites de référence et les opérations sur les limites, avec des tableaux à connaître par cœur, et une section bonus sur les limites des suites géométriques. En ce qui concerne la méthode, il y aura quatre approches principales : l'application de la définition formelle dans certains exercices, l'utilisation des limites de référence et des opérations pour prédire certaines limites, le travail supplémentaire nécessaire pour d'autres cas, et enfin un rappel sur la somme des termes d'une suite géométrique et quand cette somme peut avoir une limite.
Révisions Maths lycée
Analyse Terminale
BCPST

Limite finie
Dans cette vidéo, l'auteur aborde la notion de limite réelle en mathématiques. Il explique que la limite réelle est la valeur vers laquelle une suite tend intuitivement lorsque n augmente. Pour mieux comprendre cette notion, l'auteur utilise l'idée de couloir. Un couloir est un intervalle autour de la limite où tous les termes de la suite sont contenus à un certain moment. La définition officielle de la limite est que si tous les intervalles autour de la limite contiennent tous les termes de la suite à un moment donné, alors la limite est valide. L'auteur illustre cette idée graphiquement en prenant des exemples de suites qui convergent vers un réel. Il montre comment, en réduisant la taille du couloir, tous les termes de la suite peuvent être inclus à un moment donné. Il explique également que la convergence peut se faire de différentes manières : en croissance, en décroissance ou en oscillations. L'auteur conclut en invitant les spectateurs à poser des questions dans la FAQ et annonce la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

En l'infini
Une limite infinie en mathématiques est atteinte lorsque les termes d'une suite augmentent sans fin ou diminuent sans fin. Dans le cas d'une limite tendant vers l'infini, cela signifie que pour n'importe quel plateau donné, la suite finira par dépasser ce plateau et aura tous ces termes au-dessus de ce plateau. Cela signifie essentiellement que la suite peut continuer à augmenter indéfiniment. De manière similaire, une limite tendant vers moins l'infini signifie que pour n'importe quel plateau donné, la suite finira par être en dessous de ce plateau et continuera à diminuer indéfiniment. Ces concepts sont illustrés graphiquement avec des exemples de suites croissantes et décroissantes. Une compréhension claire de ces propriétés est importante pour résoudre des exercices mathématiques et il est recommandé de se référer à la FAQ en cas de doute.
Révisions Maths lycée
Analyse Terminale
BCPST

Unicité et Divergence
Dans cette vidéo, nous complétons les informations sur la convergence et la définition des limites en mettant en évidence deux points importants.
Le premier point est que lorsqu'une limite est finie, elle est unique. En termes simples, cela signifie que si je me rapproche d'une valeur, je ne peux pas me rapprocher de deux valeurs différentes, seulement d'une seule. C'est l'idée intuitive derrière ce concept.
Le deuxième point concerne le vocabulaire utilisé. Nous utilisons le terme "convergence" pour décrire une suite qui a une limite finie. Cependant, il est important de noter que ne pas être convergent ne signifie pas automatiquement tendre vers l'infini positif ou négatif. On peut être divergent, c'est-à-dire non convergent, de différentes manières. Nous illustrons ainsi un cas de divergence vers l'infini positif ou vers l'infini négatif.
Il existe un cas un peu différent qui est celui de l'oscillation. Par exemple, si nous prenons la suite (-1)^n, où n est un entier, celle-ci vaut 1 lorsque n est pair, -1 lorsque n est impair, et ainsi de suite. Cette suite oscille entre -1 et 1, et ne converge donc ni vers -1 ni vers 1. Elle ne tend pas non plus vers l'infini positif ou négatif. C'est un exemple de suite non convergente mais qui ne tend pas non plus vers l'infini, elle a simplement un comportement d'oscillation permanent.
Il est important de souligner qu'il est possible d'extraire des sous-suites à partir de suites plus générales, mais cela dépasse le programme scolaire et n'est pas abordé ici. On peut extraire les termes qui restent bloqués à 1 et dire que cela tend vers 1. Cependant, dans l'ensemble, cette suite n'a pas de limite, elle oscille entre deux valeurs et ne tend pas vers l'infini.
En conclusion, nous avons vu qu'une limite finie est unique et qu'une suite peut être divergente sans tendre vers l'infini positif ou négatif. Il est également possible d'avoir des suites qui oscillent entre deux valeurs sans avoir de limite définie. Si vous souhaitez plus de détails, consultez la FAQ ou discutez avec nous. À bientôt !
Révisions Maths lycée
Analyse Terminale
BCPST

Limites de référence et opérations
Ce cours traite des outils pratiques pour comprendre les limites de suites mathématiques.
Tout d'abord, on apprend que les puissances positives de n (n, n², n³, etc.) tendent vers l'infini lorsque n tend vers l'infini. De même, les puissances négatives de n (1/n, 1/n², etc.) tendent vers zéro.
Ensuite, on découvre comment gérer les opérations sur différentes suites. La somme de deux suites qui tendent vers une limite finie a pour limite la somme de ces limites. Si une suite tend vers l'infini et l'autre vers une limite finie, c'est l'infini qui l'emporte. De même, si les deux suites tendent vers l'infini ou vers moins l'infini, la limite de leur somme est également infinie ou moins l'infini.
Cependant, il existe des cas où la limite est indéterminée, c'est-à-dire qu'il n'y a pas de règle préétablie. Dans ces cas, il faut analyser chaque situation spécifique.
Enfin, le cours aborde les formes indéterminées dans le cas de produits et quotients de suites. Il y a quatre cas à retenir : plus l'infini sur plus l'infini, zéro sur zéro, zéro fois plus l'infini et zéro fois moins l'infini. Il est important de connaître ces formes et de les reconnaître lors des exercices.
En conclusion, il est recommandé d'apprendre les tables de limites par cœur et de comprendre les formes indéterminées pour être prêt à résoudre les exercices.
Révisions Maths lycée
Analyse Terminale
BCPST

Suites géométriques - illustration
Dans cette vidéo, nous abordons le sujet des suites géométriques et leurs différents comportements en fonction de leur raison Q.
Lorsque Q est supérieur à 1, il est dit que la suite converge vers l'infini. Par exemple, si nous prenons Q égal à 3, chaque terme sera plus grand que le précédent et la suite augmentera rapidement.
Quand Q est compris entre -1 et 1, la suite tend vers 0. Par exemple, si nous prenons Q égal à 0,5, chaque terme sera la moitié du précédent et la suite diminuera progressivement jusqu'à 0.
Si Q est égal à 1, la suite restera constante et égale à 1.
Si Q est inférieur à -1, la suite diverge, mais ne tend ni vers l'infini ni vers moins l'infini. La suite oscille entre des valeurs positives et négatives.
Ces différents comportements peuvent être illustrés graphiquement. Par exemple, pour Q égal à 2, la suite sera une courbe exponentielle croissante.
Pour Q compris entre -1 et 1, nous pouvons tracer des points qui convergent progressivement vers 0. Si Q est négatif, la suite oscille entre des valeurs négatives et positives, mais converge également vers 0.
Pour Q égal à 1, la suite reste constante à 1.
Enfin, pour Q inférieur à -1, la suite diverge et oscille entre des valeurs positives et négatives.
Il est important de comprendre visuellement ces différents cas pour mieux appréhender le sujet. Dans la prochaine vidéo, nous entrerons plus en détail dans la démonstration mathématique de ces comportements.
Révisions Maths lycée
Analyse Terminale
BCPST

Suites géométriques : démo
Dans cette vidéo, nous démontrons les résultats graphiques sur les limites des suites géométriques. Nous discutons plusieurs cas. Le premier cas concerne Q étant strictement supérieur à 1, et nous démontrons que Q à la puissance n tend vers l'infini. Pour cela, nous utilisons l'inégalité de Bernoulli et le terrain de comparaison. En posant Q égal à 1 plus h, où h est un nombre positif, nous pouvons appliquer l'inégalité de Bernoulli pour montrer que 1 plus h à la puissance n est supérieur ou égal à 1 plus nh. Comme nh est une suite arithmétique tendant vers l'infini, nous concluons que Q à la puissance n tend également vers l'infini. Les autres cas peuvent être démontrés en utilisant des astuces mathématiques similaires. Par exemple, pour Q compris entre 0 et 1, nous posons P égal à 1 sur Q, et appliquons les résultats précédents pour montrer que P à la puissance n tend vers l'infini, ce qui implique que Q à la puissance n tend vers 0. Pour le dernier cas, nous utilisons le théorème des gendarmes, qui permet de comparer une suite à des bornes et d'en déduire sa limite. En posant s égal à moins Q, nous montrons que s à la puissance n tend vers 0 et que Q à la puissance n est compris entre -s à la puissance n et s à la puissance n. Par conséquent, Q à la puissance n tend également vers 0. Ces démonstrations sont importantes et doivent être mémorisées. N'hésitez pas à poser des questions ou à consulter la FAQ pour une meilleure compréhension.
Révisions Maths lycée
Analyse Terminale
BCPST

Limite avec A ou Ɛ
Ce cours traite de la définition formelle d'une limite en mathématiques. Il explique comment ne pas avoir peur de cette définition en utilisant des exemples. La définition consiste à montrer qu'à partir d'un certain rang, la suite des termes d'une fonction sera toujours supérieure à un réel donné. Peu importe la valeur de ce réel, tant qu'elle est supérieure à zéro. L'équation à résoudre est 3n + 2 > A, avec A > 0. En utilisant les propriétés de la partie entière d'un réel, on peut trouver l'entier n0 à partir duquel cette inégalité est toujours vraie. La définition formelle de la limite est que pour toute valeur de A, il existe un rang n0 à partir duquel tous les termes de la suite sont supérieurs à A. Des exemples et un schéma sont donnés pour illustrer cette notion. Malgré sa complexité apparente, la définition formelle de la limite n'est pas si compliquée une fois qu'on s'y habitue. En cas de questions, il est conseillé de consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Forme indéterminée 1 : factoriser par terme de plus haut degré
Dans ce cours, nous abordons les méthodes pour calculer les limites de formes indéterminées. Un exemple courant concerne les polynômes en "n". Pour déterminer la limite dans ce cas, nous utilisons la règle selon laquelle seul le terme de plus haut degré compte et prédomine. Pour démontrer cela rigoureusement, nous factorisons par le terme de plus haut degré. Par exemple, si le terme de plus haut degré est "n²-n", en factorisant par "n²", nous obtenons "1 + 1/n". Comme le terme "1/n" tend vers 0, nous n'avons plus de formes indéterminées et obtenons "plus l'infini fois 1", ce qui tend vers "plus infini". En conclusion, cette méthode fonctionne pour tous les polynômes. Nous factorisons par le terme de plus haut degré, et c'est le coefficient devant ce terme qui détermine la limite. Dans cet exemple, le coefficient est 1, ce qui donne une limite de "plus infini". C'est ainsi que nous déterminons les limites pour les polynômes avec une limite "plus infini".
Révisions Maths lycée
Analyse Terminale
BCPST

Forme indéterminée 2 : la quantité conjuguée
Dans ce cours, nous étudions les fonctions rationnelles, qui sont des polynômes divisés par d'autres polynômes. Pour obtenir la fonction rationnelle, nous devons factoriser par le terme de plus haut degré.
Dans l'exemple donné, nous avons la suite Vn égale à 4n² sur n plus 1. Nous identifions le terme de plus haut degré, qui est de degré 2, et nous factorisons par n². En bas, le terme de plus haut degré est de degré 1, donc nous factorisons par n. Les n se simplifient en partie, et nous avons 4n au numérateur divisé par 1 plus 1 sur n qui tend vers 1. Ainsi, nous levons l'indétermination et nous constatons que le quotient tend vers plus infini. En conclusion, Vn tend vers plus infini.
En étudiant d'autres cas de figure, nous observons trois possibilités. Si le degré de P est strictement supérieur au degré de Q, P l'emporte et la limite tend vers plus infini. Si le degré de Q est strictement supérieur au degré de P, Q l'emporte et la limite tend vers 0. Enfin, si le degré de Q est égal au degré de P, le rapport des coefficients dominants tend vers un réel.
Pour illustrer ces cas, nous prenons l'exemple de la suite Un égale à 3n² plus 2n plus 1 sur 4n² plus n plus 4. En factorisant par le terme de plus haut degré, n² en haut et en bas, nous simplifions l'expression. Finalement, la limite tend vers 3 quarts, qui est le rapport des coefficients dominants.
Il est important de noter que ces trois cas sont systématiques lorsqu'il s'agit de fonctions rationnelles. Voilà pour la méthode sur les fonctions rationnelles.
Révisions Maths lycée
Analyse Terminale
BCPST

Limite d'une somme géométrique
En résumé, ce cours explique qu'en mathématiques, lorsqu'on a une limite à calculer, il n'y a pas toujours de nombreuses méthodes disponibles. Il est important de regarder les termes de la somme pour déterminer s'il s'agit d'une suite arithmétique, d'une suite géométrique ou autre. Dans ce cas précis, il s'agit de termes consécutifs d'une suite géométrique. La formule est utilisée pour calculer la somme en identifiant les valeurs de u0 (le premier terme) et q (le facteur de la suite géométrique). Il est essentiel de vérifier si l'expression est cohérente en termes d'indices. La formule de la somme de termes consécutifs d'une suite géométrique est appliquée pour obtenir le résultat final. En utilisant cette formule, il est démontré que la somme tend vers l'infini.
Révisions Maths lycée
Analyse Terminale
BCPST

Trouver à la calculette "le plus petit entier tel que..."
Dans ce cours, nous étudions une suite et essayons de trouver le plus petit entier tel que la valeur de la suite soit supérieure à une certaine valeur. La suite commencée par 0, 2 et a la relation de récurrence un+1 = 3un. Nous pouvons voir que chaque terme de la suite est obtenu en multipliant le terme précédent par 3. Donc, on sait que la suite tend vers l'infini. En utilisant un programme, nous voulons déterminer à quel rang de la suite le terme est supérieur à 1000. Pour cela, nous utilisons une boucle while avec la condition tant que u est inférieur à 1000. À chaque itération, nous multiplions u par 3 et incrémentons n de 1 pour compter le nombre d'opérations. À la fin, nous affichons la valeur de n, qui nous donne le rang de la suite. En utilisant la méthode du calcul manuel, nous constatons que la valeur de u augmente très rapidement. Nous trouvons que u3 = 54, u4 = 162, u5 = 486, et u6 = 1458. Donc, le premier entier pour lequel u est supérieur à 1000 est 6. Donc, en résumé, ce cours explique comment trouver le rang de la suite à partir d'un certain seuil en utilisant un programme simple.
Révisions Maths lycée
Analyse Terminale
BCPST
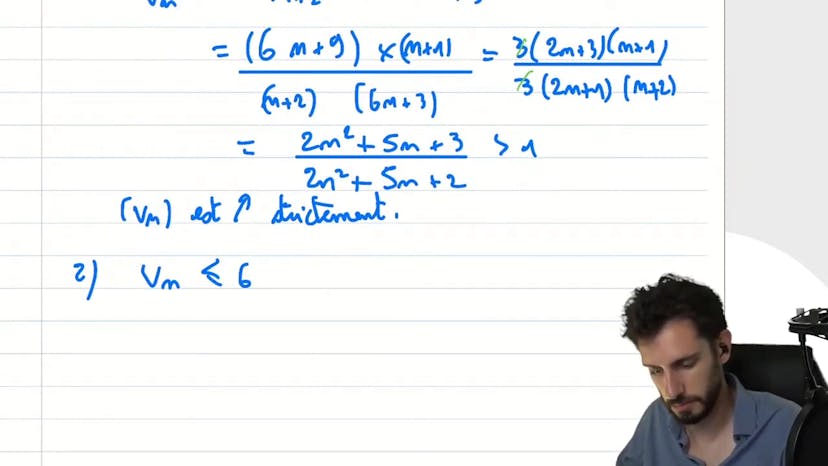
Suite-fraction
Le cours aborde la convergence d'une suite VN qui est définie par la formule 6N+3 sur N+1. Pour étudier les variations de la suite, on utilise le critère de croissance en comparant VN+1 divisé par VN à 1. On démontre que ce ratio est supérieur à 1, ce qui signifie que la suite VN est strictement croissante. Ensuite, on montre que la suite est majorée par 6 en montrant que VN plus 6 est égal à 6. Enfin, on applique le théorème de convergence monotone pour conclure que la suite VN converge. On peut également résumer cela en une seule ligne en manipulant l'expression de VN et en utilisant la fonction f(x) = 6-3/(x+1). On observe que f est croissante, VN est donc croissante, et on déduit que la suite converge vers 6.
Révisions Maths lycée
Analyse Terminale
BCPST

Plein de limites !
Il s'agit d'une transcription d'une vidéo sur différentes méthodes de gestion des limites. Les deux principales méthodes abordées sont la méthode du terme dominant et la méthode de l'encadrement. La méthode du terme dominant consiste à comparer les termes dominants en haut et en bas pour déterminer la limite d'une fraction. Il est également possible de factoriser en haut et en bas par le terme dominant pour simplifier la limite. La méthode de l'encadrement est utilisée lorsque des puissances négatives ou des fonctions trigonométriques sont présentes. Il suffit d'encadrer ces termes entre -1 et 1 et d'appliquer un théorème d'encadrement pour obtenir la limite. Enfin, différentes applications de ces méthodes sont présentées pour déterminer les limites de suites.
Révisions Maths lycée
Analyse Terminale
BCPST

Téléscopage !
Ce cours porte sur les limites de suites définies comme des sommes de termes d'autres suites.
Le premier point abordé est la détermination de la limite de la suite Un, qui est égale à 1/n. On conclut que Un tend vers 0.
Ensuite, on doit montrer que pour toute valeur n appartenant à l'ensemble N (ensemble des entiers naturels), Un est égal à 1/n - 1/(n+1). On utilise une méthode de démonstration en partant de cette expression et en simplifiant jusqu'à retomber sur Un. On est ainsi en mesure de prouver cette égalité.
Finalement, on nous demande de calculer la somme Sn de la suite Un. On utilise la relation trouvée dans la question précédente, qui permet de réécrire Sn. Cette réécriture simplifie la somme en éliminant plusieurs termes, grâce à une propriété appelée somme télescopique. On en déduit que la limite de Sn lorsque n tend vers l'infini converge vers 1.
Ainsi, on peut conclure que la limite de la suite Un tend vers 0, et la limite de la somme Sn tend vers 1 lorsque n tend vers l'infini.
Révisions Maths lycée
Analyse Terminale
BCPST

Majoration astucieuse
La suite Vn = 6n + 3 / n + 1 est étudiée dans ce cours. On commence par analyser ses variations en utilisant le critère de croissance avec le ratio Vn+1 / Vn. On démontre que ce ratio est supérieur à 1, ce qui signifie que Vn est strictement croissante. Ensuite, on montre que la suite est majorée par 6 en comparant les deux expressions. En utilisant le théorème de convergence monotone, on conclut que la suite Vn est convergente.
Une autre méthode est ensuite présentée, où l'on exprime Vn sous une autre forme en utilisant la division par n + 1. En simplifiant cette expression, on montre que Vn est croissante. En analysant cette nouvelle expression, on déduit rapidement que Vn est majorée par 6. Finalement, on utilise le fait que la limite de 3 / n + 1 tend vers 0 pour conclure que la suite Vn converge vers 6.
Révisions Maths lycée
Analyse Terminale
BCPST
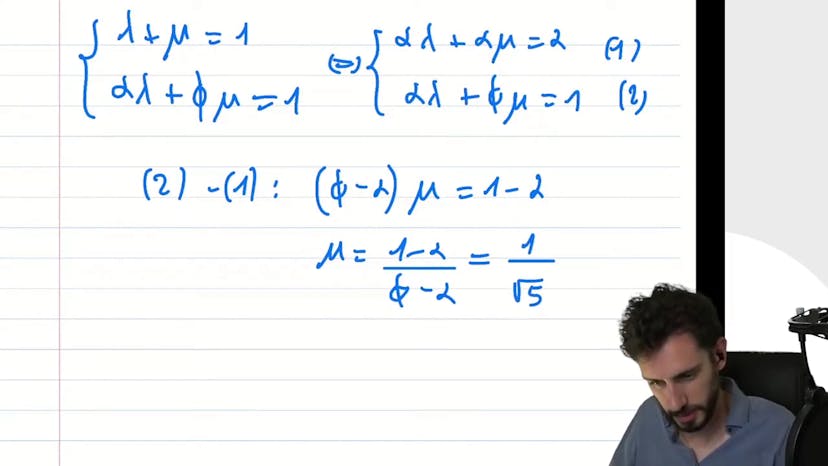
Prépa : Fibonacci
Le cours parle de la suite de Fibonacci et du nombre d'or. La suite de Fibonacci est définie par récurrence, où chaque terme est la somme des deux termes précédents. Pour calculer les termes de la suite, on a besoin des deux premiers termes, qui sont tous deux égaux à 1.
L'objectif est de trouver des réels a, b, lambda et mu tels que chaque terme de la suite puisse être exprimé comme une combinaison linéaire de termes géométriques.
Plutôt que de tenter de résoudre les quatre inconnues simultanément, il est plus judicieux de considérer les termes géométriques qui pourraient vérifier cette relation. En effectuant cette approche, on trouve deux termes possibles : a = (1 - √5)/2 et b = (1 + √5)/2 (le nombre d'or).
En utilisant ces deux termes, on peut alors résoudre un système d'équations pour trouver les valeurs de lambda et mu. Les valeurs obtenues sont lambda = (-1 + √5)/√5 et mu = (1 + √5)/(2√5).
En analysant les propriétés des termes géométriques, on peut conclure que b^n tend vers b, tandis que a^n tend vers 0 car a est compris entre 0 et -1. Par conséquent, la limite de la somme des termes de la suite de Fibonacci divise le nombre d'or par la racine carrée de 5.
En résumé, la suite de Fibonacci et le nombre d'or sont des sujets abordés dans le cours. On cherche à exprimer les termes de la suite comme une combinaison linéaire de termes géométriques, et on trouve deux termes possibles. La limite de la somme des termes de la suite divise le nombre d'or par la racine carrée de 5.
Révisions Maths lycée
Analyse Terminale
ECG

Intro Suites et limites
Dans cette vidéo, nous abordons le concept de limite de suite. Une limite de suite se produit lorsque les valeurs de la suite tendent à se rapprocher d'une certaine valeur, appelée limite. Pour illustrer cela, nous avons tracé une suite où les valeurs semblent se rapprocher d'une valeur plateau.
Cependant, afin d'être plus précis, nous devons utiliser des définitions formelles, même si elles peuvent sembler compliquées. Ces définitions impliquent des notations mathématiques et des concepts tels que les intervalles infinis et les seuils de convergence.
Néanmoins, nous allons essayer de rendre ces concepts plus accessibles en les expliquant de manière intuitive et en les reliant toujours au graphique. Bien sûr, il sera important de maîtriser ces définitions, mais à long terme, nous pourrons nous en passer.
Il est intéressant de noter que cela est similaire à lorsque nous avons appris la dérivée en première. Au début, nous avons dû nous appuyer sur la définition du taux d'accroissement, mais ensuite, nous avons simplifié les choses en utilisant une table de dérivées classiques. De même, pour les limites de suite, nous aurons des définitions formelles mais aussi des tableaux de limites classiques à connaître.
En résumé, voici les principaux points du cours : la définition des limites à l'infini, des limites négatives infinies, et des limites en un point réel, ainsi que la propriété d'unicité de la limite. Nous aborderons également les limites de référence et les opérations possibles sur les limites, en présentant les tableaux que vous devrez connaître par cœur. Enfin, nous aurons une section bonus sur les limites des suites géométriques.
Concernant la méthodologie, nous avons retenu quatre approches principales. La première consiste à appliquer la définition formelle dans certains exercices. Ensuite, nous verrons que certaines limites peuvent être prédites grâce aux limites de référence et aux opérations sur les limites. Cependant, dans d'autres cas, un peu plus de travail sera nécessaire. Enfin, nous ferons un rappel sur la somme des termes d'une suite géométrique et étudierons les conditions dans lesquelles cette somme peut avoir une limite.
N'hésitez pas à poser des questions dans la FAQ si vous en avez besoin, et je vous retrouverai dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
ECG

Limite finie
La limite réelle en mathématiques est la valeur vers laquelle une variable converge intuitivement à mesure que cette variable augmente. La notion de couloir est utilisée pour définir plus précisément cette limite. Dans cette vidéo, deux points sont abordés : la définition du couloir et l'illustration de différentes manières de convergence vers une limite réelle, que ce soit de manière progressive ou chaotique. La définition officielle de la limite stipule que si l'on peut trouver un intervalle autour de la limite réelle qui finit par contenir tous les termes d'une suite à un certain moment, alors on peut dire que cette limite est valide. Une image graphique est utilisée pour illustrer cette notion de couloir et pour vérifier si tous les termes de la suite sont compris dans ce couloir à partir d'un certain point. Si cela est vrai pour tous les couloirs de toutes les tailles, alors la limite est valide. Différents exemples sont donnés pour montrer que la convergence peut se faire de manière croissante, décroissante ou en oscillant autour de la limite réelle. En conclusion, la vidéo explique que la notion de limite réelle est plus complexe qu'elle en a l'air, car il y a différentes manières de converger vers cette limite et la taille du couloir peut varier.
Révisions Maths lycée
Analyse Terminale
ECG

En l'infini
Dans cette vidéo, nous abordons la notion de limite infinie. Une suite tend vers plus l'infini lorsque, pour toute valeur de plateau, la suite finira par dépasser ce plateau et avoir tous ses termes au-dessus de celui-ci. Cela signifie que la suite peut atteindre des valeurs de plus en plus élevées. Cette idée est illustrée graphiquement avec une suite croissante basée sur la parabole 𝑋². On montre que pour n'importe quelle valeur de plateau, il existe un rang où tous les termes de la suite sont au-dessus de ce plateau. De manière similaire, nous abordons la limite vers moins l'infini, où une suite décroissante finira par être en dessous de n'importe quelle valeur de plateau, même si celle-ci est très basse. Cette symétrie entre les limites infinies positives et négatives est importante à comprendre et à retenir pour les exercices et les méthodes classiques.
Révisions Maths lycée
Analyse Terminale
ECG

Unicité et Divergence
Dans cette vidéo, nous parlons de la convergence et des limites dans le contexte mathématique.
Le premier point important est que lorsque nous avons une limite finie, elle est unique. En d'autres termes, si nous nous approchons d'une certaine valeur, nous ne pouvons nous approcher que de cette valeur et non de plusieurs valeurs. Cela est assez intuitif.
Le deuxième point concerne le vocabulaire utilisé. Une suite est dite convergente lorsqu'elle a une limite finie. Cependant, il est essentiel de noter que l'absence de convergence ne signifie pas automatiquement tendre vers l'infini (positif ou négatif). C'est pourquoi nous avons distingué précisément les cas de divergence vers l'infini ou moins l'infini. Cela sous-entend qu'il est possible de diverger, de ne pas converger autrement.
Il existe un cas un peu particulier, celui de l'oscillation, qui illustre cette idée. Par exemple, si nous prenons la suite (-1)^n, qui vaut 1 lorsque n est pair et -1 lorsque n est impair, elle oscille. Cette suite ne converge ni vers -1 ni vers 1, elle n'a donc pas de limite finie. Elle ne tend pas non plus vers l'infini positif ou négatif. Elle présente simplement un comportement d'oscillation permanent.
On pourrait penser qu'il existe une petite convergence pour les termes du haut de la suite, qui restent bloqués à 1, et une convergence pour les termes du bas. Cependant, cela ne fait pas partie du programme scolaire et relève de notions avancées, telles que l'extraction de sous-suites à partir de suites plus générales. On pourrait extraire les termes du haut et dire qu'ils tendent vers 1. Mais dans l'ensemble, il n'y a aucune limite, aucun horizon, il y a juste cette oscillation permanente.
Voilà, c'était le dernier exemple que je voulais vous donner. Si vous souhaitez plus de détails ou en savoir davantage, n'hésitez pas à consulter la FAQ ou à discuter avec nous. À bientôt !
Révisions Maths lycée
Analyse Terminale
ECG

Limites de référence et opérations
Dans ce cours, nous abordons les outils pratiques liés à la convergence et la divergence des suites. Nous commençons par les puissances de n, qui tendent vers l'infini lorsque n tend vers l'infini. Les puissances positives de n, y compris les racines de n, ont tendance à tendre vers plus l'infini. De plus, ces fonctions augmentent de plus en plus vite à mesure que la puissance augmente. En revanche, les puissances négatives de n, telles que 1/n, tendent vers zéro car elles représentent 1 divisé par un nombre très grand.
Nous abordons ensuite les opérations sur les suites. La limite de la somme de deux suites est la somme des limites de chaque suite. Par exemple, si une suite tend vers l'infini et une autre vers une limite finie, leur somme tendra vers l'infini. Nous considérons également les cas où les deux suites tendent vers l'infini ou vers moins l'infini, où la somme sera respectivement l'infini ou moins l'infini.
Nous introduisons ensuite le concept de forme indéterminée. Il s'agit de cas où il n'existe pas de règle prédéterminée pour déterminer la limite d'une expression. Nous donnons des exemples où une suite tendant vers l'infini est combinée avec une suite tendant vers moins l'infini, et les résultats varient entre zéro et l'infini. Nous mentionnons également d'autres formes indéterminées, telles que le produit de deux suites où l'une tend vers zéro et l'autre vers l'infini, ainsi que le quotient de deux suites où l'une tend vers l'infini et l'autre vers zéro. Nous soulignons l'importance de reconnaître ces formes indéterminées et d'appliquer la méthode appropriée pour les résoudre.
En conclusion, il est crucial de mémoriser les propriétés des puissances de n et de retenir les quatre formes indéterminées : plus l'infini, moins l'infini, zéro fois plus l'infini et zéro fois moins l'infini. En connaissant ces concepts, vous serez prêt à résoudre les exercices liés à la convergence et à la divergence des suites. Restez à l'écoute pour la prochaine vidéo !
Révisions Maths lycée
Analyse Terminale
ECG

Suites géométriques - illustration
Ce cours traite de la convergence et de la divergence des suites géométriques, en cherchant à les comprendre intuitivement. Il présente plusieurs comportements en fonction de la valeur de la raison (Q) de la suite.
Lorsque Q est supérieur à 1, la suite tend vers l'infini. Par exemple, si Q est égal à 3, les termes de la suite augmentent de plus en plus rapidement.
Lorsque Q est compris entre -1 et 1, la suite converge vers 0. Par exemple, si Q est égal à 0.5, chaque terme est la moitié du précédent, et la suite tend vers 0.
Lorsque Q est égal à 1, la suite converge vers 1.
Lorsque Q est inférieur à -1, la suite diverge sans limite spécifique. Par exemple, si Q est égal à -0.7, chaque terme de la suite oscille autour de 0 sans jamais converger vers une valeur précise.
Ces comportements peuvent être illustrés graphiquement. Par exemple, pour une suite avec une raison de 2, les termes augmentent exponentiellement.
Pour une suite avec une raison entre -1 et 1, les termes tendent vers 0, soit de manière directe (cas positif), soit en oscillant autour de 0 (cas négatif).
Pour une suite avec une raison de 1, tous les termes sont égaux à 1.
Pour une suite avec une raison inférieure à -1, les termes s'écartent de 0, en s'écartant alternativement du côté positif et du côté négatif.
En comprenant visuellement ces différents comportements, on retient que les suites géométriques convergent lorsque la raison est proche de 0, et qu'elles divergent lorsque la raison est éloignée de 0.
Révisions Maths lycée
Analyse Terminale
ECG

Suites géométriques : démo
Le cours porte sur la démonstration de limites de suites géométriques. Dans le premier cas, lorsque Q est strictement supérieur à 1, on démontre que Q puissance n tend vers plus infini. On utilise ici l'inégalité de Bernoulli et le terrain de comparaison pour comparer Q avec une autre suite qui tend vers plus infini. Dans le deuxième cas, lorsque Q est entre 0 et 1, on pose P égale à 1 sur Q et on applique le résultat du premier cas. Ainsi, P puissance n tend vers plus infini, ce qui implique que Q puissance n tend vers 0. Dans le dernier cas, on utilise le théorème des gendarmes pour encadrer Q puissance n entre deux suites qui convergent vers 0. Ainsi, on conclut que Q puissance n tend également vers 0. Cette démonstration utilise des astuces mathématiques pour simplifier les calculs et obtenir les résultats facilement.
Révisions Maths lycée
Analyse Terminale
ECG

Limite avec A ou Ɛ
Dans ce cours, nous abordons la définition mathématique d'une limite et son utilité pour ceux qui poursuivent l'étude des mathématiques. Nous commençons par définir une suite U_n égale à 3n plus 2. Nous voulons montrer que pour tout réel A supérieur à 0, il existe un plus petit entier naturel n_0 tel que si n est supérieur à n_0, alors U_n est supérieur à A.
En d'autres termes, nous voulons montrer que quel que soit le seuil A que nous fixons, même s'il est très grand, il existe un rang n_0 à partir duquel tous les termes de la suite sont supérieurs à ce seuil. Cette définition correspond à la limite lorsque n tend vers l'infini.
Pour résoudre cette équation, nous avons besoin de trouver un entier n_0 à partir duquel cette inégalité est toujours vraie. En résolvant l'équation 3n plus 2 supérieur à A, nous obtenons n supérieur à (A moins 2) divisé par 3.
Cependant, nous devons faire attention car n est un entier naturel. Pour garantir que n_0 est également un entier, nous utilisons la partie entière de (A moins 2) divisé par 3 plus 1.
Cette partie entière correspond à B, un réel qui n'est pas nécessairement un entier. Cependant, nous pouvons prendre la partie entière de B plus 1 pour obtenir n_0, qui est bien un entier.
Ainsi, le plus petit entier n_0 tel que n est supérieur à n_0 et que U_n est supérieur à A peut être écrit comme la partie entière de (A moins 2) divisé par 3 plus 1.
Cette définition correspond à la limite lorsque n tend vers l'infini, où quel que soit le seuil que nous fixons, il existe un rang à partir duquel tous les termes de la suite sont au-dessus de ce seuil.
Cette méthode montre que même si nous fixons un seuil très élevé, nous trouverons toujours un rang à partir duquel les termes de la suite dépassent ce seuil. Cela illustre la définition formelle de la limite en mathématiques.
Bien que les définitions formelles puissent sembler complexes au début, elles deviennent plus faciles à comprendre avec la pratique. Si vous avez des questions, consultez la FAQ pour plus d'informations.
Révisions Maths lycée
Analyse Terminale
ECG

Forme indéterminée 1 : factoriser par terme de plus haut degré
Ce cours traite des différentes formes indéterminées pour le calcul de limites et les méthodes pour les résoudre. Une des formes indéterminées les plus courantes est celle d'un polynôme en n. Pour résoudre cette forme indéterminée, on utilise la règle qui stipule que seul le terme de plus haut degré est important et prédomine. Pour démontrer cela de manière rigoureuse, on factorise le polynôme par le terme de plus haut degré. Dans l'exemple donné (n²-n), on factorise par n², ce qui donne 1+1/n. Comme 1/n tend vers 0, on n'a plus de forme indéterminée et on obtient un résultat du type "plus l'infini fois 1", ce qui tend vers plus infini. Ainsi, pour tous les polynômes, on factorise par le terme de plus haut degré et c'est le coefficient devant ce terme qui détermine la limite. Dans cet exemple, le coefficient est 1, ce qui signifie que la limite est plus infini. Cela résume la méthode pour calculer les limites des polynômes lorsque n tend vers plus infini.
Révisions Maths lycée
Analyse Terminale
ECG

Forme indéterminée 2 : la quantité conjuguée
Dans ce cours, nous abordons les méthodes pour résoudre les fonctions rationnelles, qui sont des polynômes divisés par d'autres polynômes. La technique utilisée est similaire à celle utilisée pour les polynômes eux-mêmes, c'est-à-dire que nous devons factoriser par le terme de plus haut degré. Dans l'exemple donné, nous étudions la suite Vn = 4n² / (n + 1). Nous identifions que le terme de plus haut degré est de degré 2, donc nous factorisons par n². Au dénominateur, le degré est de 1, donc nous factorisons par n. Les n se simplifient partiellement, et nous obtenons 4n au numérateur divisé par (1 + 1/n), qui tend vers 1. Ainsi, nous supprimons l'indétermination et concluons que Vn tend vers l'infini positif.
En examinant les différents cas possibles, nous constatons trois situations. Premièrement, si le degré de P est strictement supérieur au degré de Q, cela signifie que P l'emporte et que l'infini de Q est moins puissant. Par conséquent, Qn tend vers l'infini positif. Deuxièmement, si le degré de Q est strictement supérieur au degré de P, c'est Q qui l'emporte et la limite de Un sera égale à 0. Enfin, si le degré de Q est égal au degré de P, alors les deux sont de même importance et la limite sera le rapport des coefficients dominants Q/P.
Prenons l'exemple de la suite Un = (3n² + 2n + 1) / (4n² + n + 4). En factorisant par le terme de plus haut degré n², nous simplifions l'expression et obtenons (3 + 2n + 1/n²) / (4 + 1/n + 4/n²). Finalement, cette expression tend vers 3/4, qui est le rapport des coefficients dominants.
Il est important de noter que ces trois cas sont systématiques et s'appliquent à toutes les fonctions rationnelles. C'est la méthode à suivre pour résoudre ces fonctions.
Révisions Maths lycée
Analyse Terminale
ECG

Limite d'une somme géométrique
Le cours porte sur le calcul d'une somme avec une limite donnée. En terminale, il n'y a pas beaucoup de méthodes pour calculer cette somme, donc il faut toujours examiner les termes de la somme pour voir s'ils correspondent à une suite arithmétique ou géométrique. Si ce n'est pas le cas, il faut faire une étude précise. Dans cet exemple, les termes de la somme correspondent à une suite géométrique, donc on peut utiliser la formule suivante : Sn = u0 * (q^n - 1) / (q-1), où u0 est le premier terme et q est la raison de la suite géométrique. En vérifiant les termes de la somme, on trouve que u0 = 1 et q = 3. En appliquant la formule, on obtient Sn = (1/2) * (3^n + 1 - 1). En analysant cette expression, on peut voir que la suite tend vers l'infini lorsque n tend vers l'infini. Par conséquent, la somme tend également vers l'infini.
Révisions Maths lycée
Analyse Terminale
ECG

Trouver à la calculette "le plus petit entier tel que..."
Dans ce cours, nous étudions une suite et cherchons à trouver le plus petit entier pour lequel la valeur de la suite est supérieure à 1000. La suite est définie comme suit : u0 = 2 et un+1 = 3un.
Pour résoudre ce problème, nous utilisons un programme simple. Nous initialisons un compteur n à 0 et une variable u à 2. Ensuite, nous entrons dans une boucle while où nous multiplions u par 3 et incrémentons n de 1 à chaque itération jusqu'à ce que u dépasse 1000. Enfin, nous imprimons la valeur de n, qui représente le rang pour lequel la valeur de la suite est supérieure à 1000.
En analysant la progression de la suite, nous pouvons voir qu'elle augmente très rapidement. En utilisant juste une calculatrice, nous avons constaté que le premier entier pour lequel un est supérieur à 1000 est n = 6.
Cette méthode peut être réalisée sans programme en effectuant des itérations simples. Cela permet de résoudre le problème rapidement. N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires sur cette méthode.
Révisions Maths lycée
Analyse Terminale
ECG
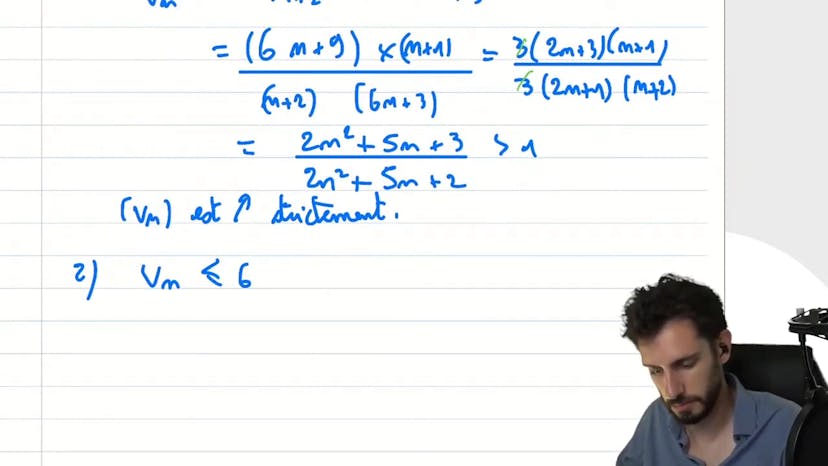
Suite-fraction
Ce cours explique comment étudier les variations et la convergence d'une suite donnée par l'expression vn = 6n + 3/n + 1. Le premier approche consiste à utiliser le critère de croissance en calculant le ratio vn+1/vn. En simplifiant cette expression, on obtient un résultat supérieur à 1, ce qui implique que la suite vn est strictement croissante. Ensuite, on démontre que la suite est majorée par 6 en montrant que vn + 6 = 6, ce qui est vrai pour tout n. Puis, en utilisant le théorème de convergence monotone, on conclut que la suite vn converge.
Une autre approche consiste à simplifier l'expression vn en écrivant vn = 6(n + 1) - 3/(n + 1). En étudiant cette nouvelle expression, on constate que la suite vn est croissante car la fonction correspondante est croissante. De plus, on peut directement affirmer que la limite de vn est égale à 6, en utilisant une limite classique.
En résumé, la suite vn = 6n + 3/n + 1 est croissante, majorée par 6, et converge vers 6.
Révisions Maths lycée
Analyse Terminale
ECG

Plein de limites !
Nous avons abordé deux méthodes de gestion des limites : la méthode du terme dominant et la méthode de l'encadrement. La méthode du terme dominant consiste à comparer les termes dominants d'une fraction pour déterminer sa limite. On peut également factoriser la fraction par le terme dominant pour simplifier le calcul. La méthode de l'encadrement, quant à elle, consiste à encadrer les différentes parties de l'expression pour obtenir une limite finie. On peut alors appliquer le théorème des gendarmes si les encadrements sont convergents. Ces techniques sont notamment utiles lorsque l'on rencontre des puissances négatives, des sinus ou des cosinus, car on peut les encadrer facilement.
Révisions Maths lycée
Analyse Terminale
ECG

Téléscopage !
Ce cours aborde les limites de suites définies comme des sommes de termes d'autres suites. On y découvre deux principales questions.
La première consiste à déterminer la limite de la suite Un, qui tend vers 0 lorsque n tend vers l'infini.
Ensuite, on nous demande de montrer que pour toutes les valeurs n, on a Un égal à 1/(n - 1) - 1/(n + 1). Plusieurs méthodes sont possibles pour résoudre cette question, mais il est préférable de partir de cette expression pour retrouver Un, plutôt que d'écrire directement Un égal à cette expression.
Dans la question suivante, nous sommes invités à calculer la somme Sn en utilisant la question précédente. En utilisant la version de Un donnée dans cette question, on peut trouver la somme télescopique Sn. En effet, en simplifiant les termes de la somme, on remarque que presque tous les termes s'annulent mutuellement, à l'exception du premier et du dernier terme. En utilisant la question précédente, on peut conclure que la somme Sn converge vers 1.
Finalement, en déduisant la limite de Sn lorsque n tend vers l'infini, on obtient une convergence vers 1.
Révisions Maths lycée
Analyse Terminale
ECG

Majoration astucieuse
Dans ce cours, nous étudions une suite Vn définie par Vn = 6n + 3 / (n + 1). Pour analyser les variations, nous utilisons le critère de croissance en examinant le ratio Vn+1 / Vn. En simplifiant cette expression, nous obtenons 2n² + 5n + 3 / (2n² + 3n). Comme ce ratio est strictement supérieur à 1, nous concluons que la suite Vn est strictement croissante.
Ensuite, nous démontrons que la suite est majorée par 6. On montre que Vn < 6 en utilisant une équivalence entre 6n + 3 < 6(n + 1), qui est toujours vrai. Ainsi, nous pouvons affirmer que Vn est majorée par 6.
Enfin, nous appliquons le théorème de convergence monotone pour montrer que la suite Vn converge. Comme nous avons déjà démontré que la suite est croissante et majorée, elle converge vers une limite. En utilisant une autre méthode, nous pouvons simplifier Vn en écriture fractionnelle en séparant la fraction en deux parties. En analysant la fonction correspondante, nous concluons également que la suite Vn est croissante. En simplifiant davantage, nous obtenons une expression équivalente à 6, ce qui prouve également que la suite est majorée par 6. Finalement, la limite de Vn est calculée en utilisant une limite classique et nous trouvons que Vn tend vers 6.
Révisions Maths lycée
Analyse Terminale
ECG
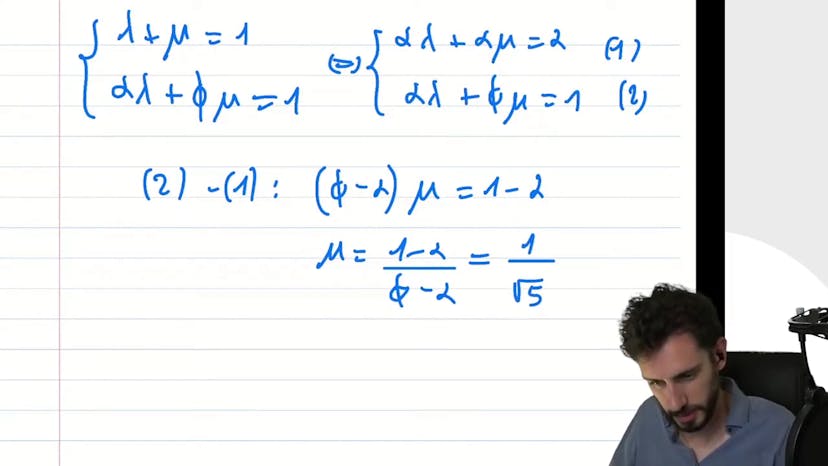
Prépa : Fibonacci
Le cours traite de la suite de Fibonacci et du nombre d'or. La suite de Fibonacci est définie par récurrence, où chaque terme est la somme des deux termes précédents. Pour trouver des réels a, b, lambda et mu tels que chaque terme de la suite puisse être exprimé comme une combinaison linéaire de sommes géométriques, on cherche des termes géométriques qui vérifient cette relation. La recherche de ces termes géométriques permet de trouver les valeurs de a et b (1 moins racine de 5 sur 2 et 1 plus racine de 5 sur 2), ainsi que lambda et mu (1 moins le nombre d'or sur racine de 5 et 1 plus le nombre d'or sur racine de 5). En analysant le comportement de ces termes géométriques, on conclut que b puissance n tend vers le nombre d'or.


