 All subjects
All subjects
 All subjects
All subjects
Maths Spé
Analyse
Terminale

Introduction
Dans ce sous-chapitre sur les intégrales, on va explorer le lien entre les méthodes de calcul d'R sous une courbe et les primitives. Ce lien va nous permettre de calculer les R de manière exacte, sans approximation. Ce qui va être intéressant, c'est que ça va aller dans les deux sens, on pourra calculer parfaitement les R sous une courbe en utilisant leurs primitives et on pourra également s'attaquer à des primitives qui ne sont pas calculables. On va aussi avoir quelques propriétés sur les intégrales en général, ainsi que des méthodes de calcul qui vont suivre ces points de courbe habituels. En somme, on va apprendre le théorème fondamental, qui définit l'existence d'une primitive avec une certaine formule pour la primitive, la condition suffisante d'existence d'une primitive, ainsi que des propriétés générales et des méthodes pour calculer une intégrale.
Maths Spé
Analyse
Terminale

Théorème fondamental : énoncé
Dans cette vidéo, l'auteur présente le théorème fondamental de l'analyse, qui relie la notion de primitive et l'intégrale d'air sous la courbe. Soit f une fonction continue et positive sur un intervalle a, b. La fonction F définie comme l'intégrale de f entre a et x est dérivable et sa dérivée est égale à f elle-même. Ainsi, F est une primitive de f. L'auteur illustre ce théorème en prenant l'exemple d'une fonction parabolique, calculant l'air sous la courbe et traçant des fonctions qui correspondent à l'air sous la courbe pour différentes valeurs de x. En examinant son dessin, il montre comment la fonction dérivée est liée à l'air sous la courbe. La vidéo s'achève sur une explication visuelle de l'interprétation graphique de la démonstration du théorème.
Maths Spé
Analyse
Terminale

Intégrale et Primitive : calcul
Dans cette vidéo, on présente une propriété fondamentale du chapitre de calcul intégral. Cette propriété permet de calculer une intégrale à l'aide d'une primitive, c'est-à-dire une fonction dont la dérivée est la fonction à intégrer. Cette propriété est distincte du théorème fondamental, qui garantit l'existence d'une primitive sous forme d'un calcul intégral. Pour démontrer cette propriété, on utilise le théorème fondamental et on distingue deux cas : si la primitive est celle du théorème fondamental, alors la propriété est prouvée facilement ; sinon, on utilise le fait que toutes les primitives d'une fonction sont de la forme de la primitive connue plus une constante, afin de prouver la propriété. On peut ainsi calculer l'aire sous la courbe d'une fonction continue pour n'importe quel intervalle.
Maths Spé
Analyse
Terminale

Propriétés 1 : intuitives !
Dans cette vidéo, nous abordons les propriétés de l'intégrale. La première est la linearité, qui mentionne que si vous prenez l'air sous une courbe, cela équivaut à multiplier la hauteur par un certain facteur. La deuxième propriété est la cumulativité, qui signifie que l'air sous une courbe combinée est la somme de l'air sous les courbes individuelles. La troisième propriété concerne les bornes, où l'air sous une courbe entre un point et lui-même est nul, et l'air entre deux points peut être pris avec un signe négatif si les points sont inversés. Enfin, la relation de Schall stipule que l'air total sous une courbe est la somme des airs entre les points où la courbe rencontre l'axe horizontal. Ces propriétés sont intuitives et faciles à comprendre pour les débutants en mathématiques.
Maths Spé
Analyse
Terminale
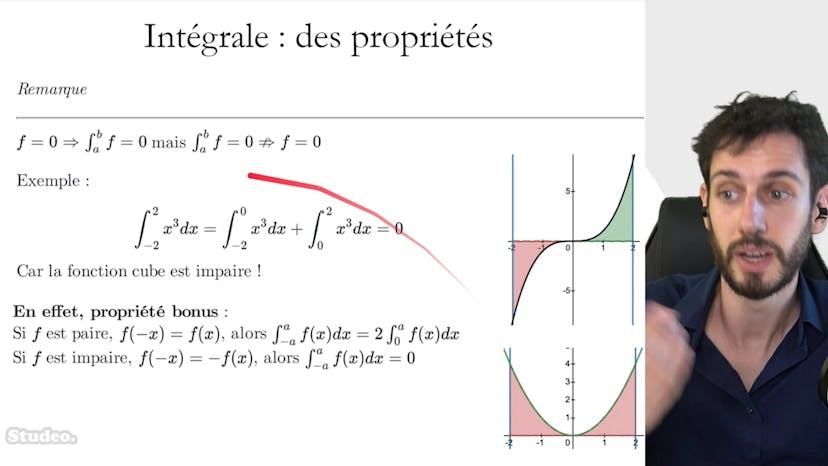
Propriétés 2 : remarques pratiques
Ce cours traite de trois propriétés importantes en mathématiques. La première propriété concerne les fonctions nulles qui ont une intégrale nulle, mais cela ne signifie pas que toutes les fonctions dont l'intégrale est nulle sont nulles aussi. La deuxième propriété traite des fonctions paires et impaires. Les fonctions paires ont une intégrale symétrique centrée sur 0, tandis que les fonctions impaires ont une intégrale nulle sur un intervalle symétrique centré sur 0. La troisième propriété concerne les fonctions périodiques, dont l'intégrale sur tout intervalle de taille t est la même. Ces propriétés sont très utiles pour résoudre des problèmes et pour gagner du temps en étudiant des fonctions.
Maths Spé
Analyse
Terminale
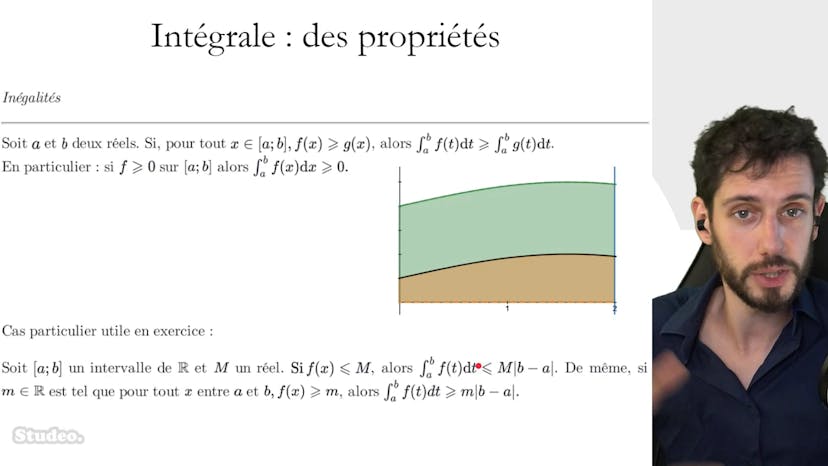
Propriétés 3 : inégalités
Dans cette vidéo, nous apprenons que les intégrales de deux fonctions f et g sont classées dans le même ordre si f est toujours plus grande que g pour toute x de a à b. Si g est la fonction nulle et que f est toujours plus grande que 0, alors l'intégrale de f est toujours positive. Si f est majorée par une fonction constante égale à M, alors l'intégrale de f est plus petite que l'intégrale de M entre a et b. Si f est minorée par une petite M, alors l'intégrale de f est plus grande que M fois b moins a en valeur absolue. Ces propriétés sont très simples, mais il est important de les connaître pour résoudre des exercices. Si vous avez des doutes, posez des questions dans la FAQ.
Maths Spé
Analyse
Terminale

Calcul d'Intégrale avec Primitive
Le cours traite de la première méthode sur le calcul intégral. L'enjeu principal du chapitre est de trouver une primitive pour l'intégrale à résoudre. L'exercice présenté consiste à calculer l'intégrale de 0 à pi de x² moins cos de 2x. Pour cela, il faut trouver une primitive. La primitive de x² est x³ et celle de cos de 2x est 1/2 sin 2x. Attention aux erreurs de signes lors de l'application du théorème fondamental, mieux vaut écrire les signes avec des parenthèses avant de développer. En simplifiant les calculs, l'intégrale finale est égale à pi au cube sur 3.
Maths Spé
Analyse
Terminale
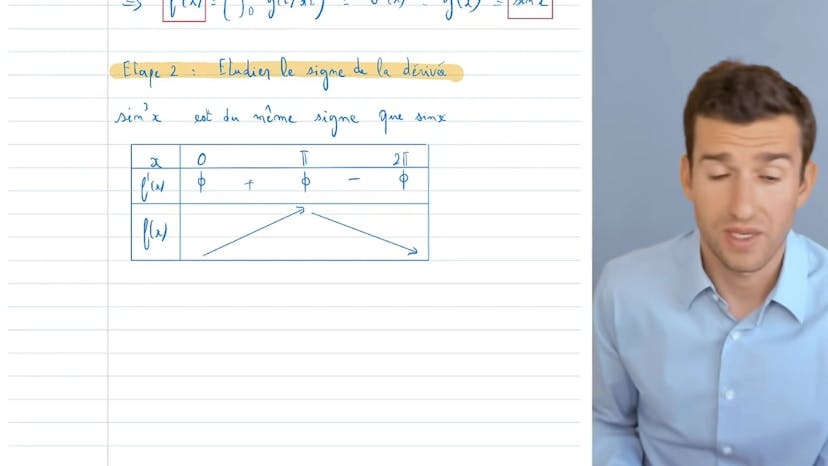
Fonction définie par une Intégrale
Étudier les variations d'une fonction peut se faire en calculant sa dérivée pour déterminer le signe, puis la monotonie. Heureusement, pour une intégrale (intégrale de a à x de u de t), sa dérivée est facile à calculer avec u. Cependant, il faut faire attention aux bornes pour que cela marche bien. Pour l'intégrale de 0 à π de sin³(t), il est donc important de faire attention au programme d'intégration pour déterminer la dérivée. Ensuite, il est facile de déduire les variations. Sin³(t) étant du même signe que sin(x), la fonction est croissante jusqu'à π/2, puis décroissante. Il est également important de faire attention aux variables si elles sont locales ou pas et de ne pas inverser les bornes.
Maths Spé
Analyse
Terminale

Linéarité d'une Intégrale
Dans ce cours de mathématiques, l'utilisation de la linéarité de l'intégrale est expliquée pour faciliter le calcul des primitifs. Le professeur nous donne un exemple, en nous faisant étudier la fonction f=x^2. Il nous demande tout d'abord de montrer que la fonction F proposée (F(x)=1/3x^3) est une primitive de f. Pour cela, il suffit de dériver F et de vérifier si la dérivée est bien égale à f. Dans la deuxième partie du cours, nous devons déterminer l'intégrale de 0 à 1 de 3x-2e^(x). Il y a une erreur d'énoncé à corriger (le t est remplacé par x). Pour trouver une primitive, le professeur rappelle la règle selon laquelle lorsque l'on a un polynôme multiplié par une exponentielle, on doit utiliser une IPP. En posant u=3x-2, et en utilisant la dérivée de u et la primitive de e^x pour v, il résout l'intégrale et trouve la primitive. Il conclut ensuite en rappelant que lorsqu'on a cette même forme de polynôme multipliée par une exponentielle, on doit toujours penser à utiliser cette méthode.
Maths Spé
Analyse
Terminale

Encadrer une Intégrale
Ce cours commence par montrer que pour tout x supérieur à 1, e de moins x carré est toujours positif. Ensuite, en utilisant les propriétés de la fonction exponentielle, on montre que cette fonction est inférieure à e de moins x. On en déduit donc un encadrement de l'intégrale de cette fonction sur l'intervalle de 1 à 2. En utilisant la propriété de monotonie de l'intégrale, on trouve finalement que cette intégrale est comprise entre 0 et e de moins 1 moins e de moins 2.
Maths Spé
Analyse
Terminale
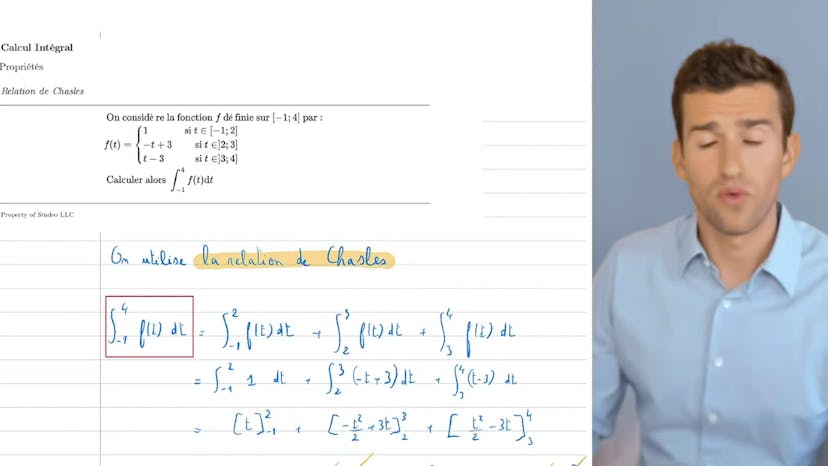
Relation de Chasles
Dans cette vidéo, l'objectif est de calculer une intégrale en utilisant les relations de Schall. On a une fonction f avec différentes expressions selon l'intervalle. Grâce à cette méthode, on peut découper l'intégrale en plusieurs morceaux et utiliser des fonctions usuelles faciles à primitiver pour les calculs. Ensuite, on vérifie que le chiffre de départ est égal à celui d'arrivée pour que ça se rejoigne bien et on peut passer par où on veut pour faire les calculs. Cette méthode est simple et facile à appliquer si on fait attention à ces détails.
Maths Spé
Analyse
Terminale
Théorème fondamental : Démo
Dans cette vidéo, l'auteur démontre le théorème fondamental de l'analyse, qui stipule que pour une fonction continue f sur l'intervalle [a, b], la fonction F définie comme l'intégrale de f entre a et x est dérivable, avec pour dérivée f. Il explique également que toute fonction continue sur un intervalle aura des primitifs sur cet intervalle. La démonstration passe par l'utilisation des propriétés des intégrales, de la méthode d'approximation par des rectangles et du théorème d'encadrement. Il est important de comprendre cette démonstration pour l'examen.
Maths SM&SP
Analyse
2BAC SM Maroc

Introduction
Dans ce sous-chapitre sur les intégrales et leur lien avec les primitives, nous allons comprendre comment calculer exactement les R sous une courbe, sans approximation. Jusqu'à présent, nous pouvions seulement trouver des approximations précises en ajoutant un nombre de rectangles, mais cela ne nous donnait pas de résultats exacts pour les fonctions autres que les fonctions affines et constantes. Nous allons découvrir qu'en réalité, il existe un lien exact entre le calcul des R et les primitives. Ce lien fonctionne dans les deux sens : nous pourrons calculer exactement les R en utilisant les primitives, mais nous pourrons aussi, grâce à ce lien, étudier des primitives qui ne sont pas calculables avec les fonctions usuelles. Par exemple, en statistique, nous avons souvent besoin de calculer la primitive de la fonction exponentielle moins x², qui est à l'origine de la courbe en cloche. Malheureusement, il n'existe pas de primitive de cette fonction avec les fonctions usuelles, ce qui nous oblige à faire une approximation numérique en calculant les R. Dans la suite du chapitre, nous verrons également différentes propriétés des intégrales, qui seront intéressantes pour les physiciens et les mathématiciens. En résumé, ce sous-chapitre aborde le lien entre les primitives et les R sous une courbe, avec le théorème fondamental, la condition suffisante d'existence d'une primitive, ainsi que des propriétés générales telles que la relation de Schall, la linéarité, la positivité et la croissance, et des inégalités. Nous aborderons également différentes méthodes pour calculer les intégrales en utilisant les primitives, la linéarité, la relation de Schall, pour encadrer une intégrale, et pour étudier les variations d'une fonction définie par une intégrale. N'hésitez pas à poser vos questions dans la FAQ et je vous retrouve dans la prochaine vidéo !
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème fondamental : énoncé
Dans cette vidéo, le professeur présente le théorème fondamental de l'analyse, qui concerne la notion de primitive et d'intégrale. Il explique que si f est une fonction continue et positive sur un intervalle [a, b], alors la fonction F définie par l'intégrale entre a et x de f sera dérivable et sa dérivée sera égale à f. Cela signifie que F est une primitive de f.
Le professeur illustre ce théorème à l'aide d'un graphique représentant une fonction parabolique négative. Il calcule alors l'aire sous la courbe entre différents points de l'intervalle et trace une fonction qui représente la valeur approximative de cette aire. Il observe que lorsque l'aire est négative, la fonction décroît, et lorsque l'aire est positive, la fonction croît.
Il souligne également que la fonction tracée ressemble à une fonction cubique, ce qui renforce l'idée que cette fonction est une primitive de la fonction initiale.
Le professeur conclut en expliquant qu'il démontrera formellement ce lien entre aire et primitive dans une prochaine vidéo, mais que cette visualisation graphique est essentielle pour comprendre cette notion. Il encourage les spectateurs à poser des questions s'ils ont besoin de précisions.
Maths SM&SP
Analyse
2BAC SM Maroc

Intégrale et Primitive : calcul
Dans cette vidéo, on présente une démonstration d'une propriété fondamentale en mathématiques. On précise qu'il y a une différence entre une propriété et un théorème. Dans ce cas, la propriété indique qu'on peut calculer une intégrale en utilisant une primitive. On utilise le théorème fondamental pour démontrer cela. On donne une fonction f continue et positive sur un intervalle a,b, et on prend une primitive F de f sur cet intervalle. On dit que l'aire entre a et b de la fonction f est égale à F(b) - F(a). On peut aussi écrire cela de manière plus compacte en utilisant la notation [F(x)]_a^b. Ensuite, on généralise cette définition pour les fonctions qui ne sont pas forcément positives en utilisant la même formule. On montre ensuite la démonstration de cette propriété en considérant deux cas : si F est la même fonction que dans le théorème fondamental, ou si F est une autre primitive de f. Dans les deux cas, on montre que l'intégrale de f entre a et b est égale à F(b) - F(a). Cette démonstration montre l'importance des primitives dans le calcul d'intégrales.
Maths SM&SP
Analyse
2BAC SM Maroc

Propriétés 1 : intuitives !
Dans cette vidéo, nous abordons les propriétés intuitives de l'intégrale. La première propriété est la linéarité. Elle dit que si vous prenez l'aire sous une courbe lambda f, cela équivaut à lambda fois l'aire sous la courbe f. De plus, si vous cumulez deux fonctions f et g, l'aire totale sera égale à l'aire de f plus l'aire de g.
En ce qui concerne les bornes, si f est une fonction continue sur un intervalle i avec a et b des réels, l'intégrale de f entre a et a est égale à zéro, car vous prenez l'aire d'un fil qui n'a pas de deuxième dimension. De plus, nous convenons que l'intégrale entre b et a est égale à l'opposé de l'intégrale entre a et b.
Enfin, la relation de Schall indique que si vous additionnez l'intégrale entre a et c et l'intégrale entre c et b, cela équivaut à l'intégrale entre a et b directement. Cela signifie que l'aire totale de la fonction est la même, quelle que soit la valeur de c.
En résumé, ces propriétés intuitives de l'intégrale sont relativement simples. Elles concernent la linéarité, les bornes et la relation de Schall. J'espère que ces explications SEO friendly vous sont claires. À bientôt pour une nouvelle vidéo sur d'autres propriétés de l'intégrale.
Maths SM&SP
Analyse
2BAC SM Maroc

Propriétés 2 : remarques pratiques
Ce cours traite des propriétés des fonctions et de leurs intégrales. La première propriété explique que si une fonction est nulle, son intégrale sera également nulle. Cependant, il est important de noter qu'une fonction dont l'intégrale est nulle sur un intervalle donné n'est pas forcément nulle elle-même. Un contre-exemple est donné pour illustrer ce point.
Ensuite, une propriété bonus est présentée : si une fonction est paire, c'est-à-dire que pour tout x, f(-x) est égal à f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera deux fois l'intégrale sur la moitié de cet intervalle. À l'inverse, si une fonction est impaire, c'est-à-dire que pour tout x, f(-x) est égal à -f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera nulle.
La dernière propriété bonus concerne les fonctions périodiques. Si une fonction a une période T, alors pour tout x, f(x+T) sera égal à f(x). De plus, l'intégrale sur un intervalle de longueur T sera égale à l'intégrale sur un intervalle de taille T centré sur 0.
Ces propriétés sont utiles pour gagner du temps dans l'étude des fonctions et leurs intégrales. Il est donc important de les comprendre et de les utiliser correctement. Le cours se termine en invitant les spectateurs à regarder la prochaine vidéo pour plus d'informations.
Maths SM&SP
Analyse
2BAC SM Maroc

Propriétés 3 : inégalités
Dans cette courte vidéo, nous abordons les propriétés de l'intégrale liées aux inégalités. Si pour tout x entre a et b, la fonction f(x) est toujours supérieure à la fonction g(x), alors leurs intégrales seront classées dans le même ordre. En d'autres termes, l'intégrale de f sera plus grande que l'intégrale de g.
Cette propriété peut être illustrée graphiquement, où l'aire sous la courbe de f est beaucoup plus grande que l'aire sous la courbe de g.
Un cas particulier intéressant est lorsque g est la fonction nulle et f est toujours supérieure à zéro. Dans ce cas, l'intégrale de f est toujours positive.
Dans le cas où f(x) est inférieure à une fonction constante m sur l'intervalle (a, b), on peut dire que m est une borne supérieure de f. Ainsi, l'intégrale de f entre a et b sera plus petite que l'intégrale de m entre a et b. Cette intégrale de m correspond à l'aire d'un rectangle, qui est égale à m multiplié par la longueur de l'intervalle (b-a).
De manière similaire, si f(x) est supérieure à une certaine constante M sur l'intervalle (a, b), on peut dire que M est une borne inférieure de f. Dans ce cas, l'intégrale de f sera plus grande que l'aire du rectangle situé en dessous, qui est égale à M multiplié par la longueur de l'intervalle (b-a).
Il est important de connaître ces propriétés. N'hésitez pas à poser vos questions dans la FAQ si vous avez des doutes. À bientôt dans la prochaine vidéo.
Maths SM&SP
Analyse
2BAC SM Maroc

Théorème fondamental : Démo
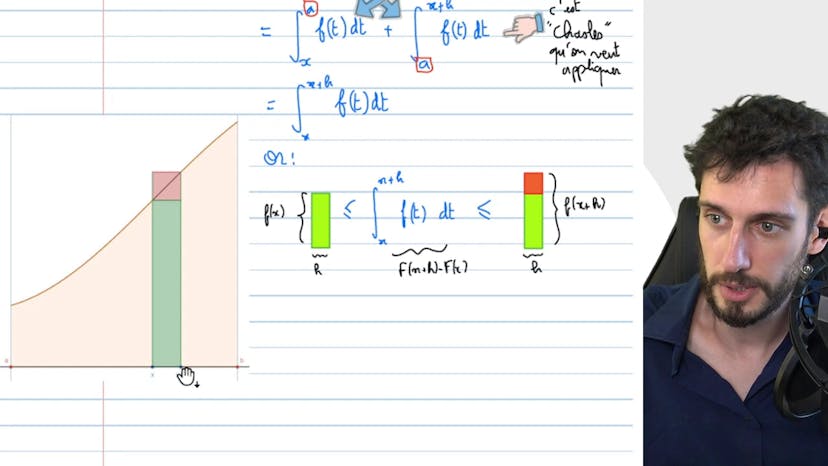
Dans cette vidéo, on démontre le théorème fondamental de l'analyse. On considère une fonction continue f sur l'intervalle [a,b] et on définit une autre fonction F comme l'intégrale de f entre a et x. On montre que F est dérivable et que sa dérivée est égale à f. On utilise la propriété de Schall pour montrer que l'erreur entre F(x+h)-F(x) et l'intégrale de f entre x et x+h est négligeable comparée à la hauteur de f(x+h). On utilise ensuite le théorème d'encadrement pour montrer que la limite du taux d'accroissement (F(x+h)-F(x))/h est égale à f(x). On conclut ainsi que F est dérivable avec pour dérivée f. En conséquence, toute fonction continue sur un intervalle a une primitive sur cet intervalle.
Maths SM&SP
Analyse
2BAC SM Maroc

Calcul d'Intégrale avec Primitive
Dans ce cours sur le calcul intégral, la première méthode est expliquée. L'objectif principal de ce chapitre est de trouver une primitive pour résoudre les intégrales. Cela peut être plus difficile que de dériver. Ainsi, la méthode consiste à trouver une primitive pour résoudre l'intégrale donnée, puis à appliquer le théorème fondamental.
Dans l'exemple présenté, l'intégrale à calculer est l'intégrale de 0 à pi de x² moins cos2x. Pour résoudre cette intégrale, il suffit de trouver la primitive de chacun des termes (x² et cos2x) séparément. La primitive de x² est x³ et la primitive de cos2x est ½ sin2x. On peut vérifier que ces primitives conviennent en dérivant et en retrouvant les termes initiaux.
En appliquant le théorème fondamental, il suffit ensuite de substituer les valeurs de la fonction primitive à la borne supérieure (pi) et à la borne inférieure (0) de l'intervalle d'intégration. Il est important de faire attention aux signes lors de cette étape afin d'éviter des erreurs courantes. Il est recommandé d'écrire les signes moins entre parenthèses avant de développer les calculs pour éviter des confusions.
Dans cet exemple, le sinus de pi est 0, donc cela n'affecte pas le signe final du résultat. Après simplification, le résultat de l'intégrale est pi au cube sur 3.
Ainsi, ce cours présente une méthode pour calculer une intégrale en trouvant une primitive et en appliquant le théorème fondamental. Le résultat obtenu pour l'intégrale donnée est pi au cube sur 3.
Maths SM&SP
Analyse
2BAC SM Maroc

Fonction définie par une Intégrale
Ce cours explique comment étudier les variations d'une fonction définie par une intégrale. Habituellement, on calcule la dérivée pour déterminer le signe de la dérivée et la monotonie de la fonction. Cependant, dans le cas d'une intégrale, la dérivée est facile à calculer. On étudie donc le signe de la dérivée pour déduire les variations de la fonction et construire un tableau de variations.
Dans cet exemple, on nous demande d'étudier les variations de la fonction f sur l'intervalle [0, pi] définie par f(x) = ∫₀ˣ sin³(t)dt. Il est important de faire attention, car le résultat dépend des bornes de l'intégrale. Par exemple, si nous prenons l'intégrale de -x à 0 de h(t), où h est une fonction quelconque et H est une primitive de h, nous devons corriger les bornes et obtenons -∫₀ˣ h(t)dt = H(0) - H(x). Lorsque nous dérivons cette fonction, nous obtenons -H'(x), et comme H est une primitive, cela correspond à -h(x). Ainsi, le signe dépend des bornes et peut être différent de ce que nous attendons.
Ensuite, nous cherchons la dérivée de f en posant G(x) = sin³(x). Appliquant le théorème fondamental du calcul, nous obtenons f(x) = G(x) - G(0), et la dérivée de f est G'(x) = sin³(x). Ainsi, nous retrouvons bien la fonction à l'intérieur de l'intégrale.
Il est important de noter que les variables x et t ont des significations différentes. t est la variable d'intégration et n'a de sens que dans l'intégrale, tandis que x est une variable globale et a une signification à l'extérieur de l'intégrale. Par conséquent, nous ne pouvons pas avoir la même variable à la fois à l'intérieur et à l'extérieur de l'intégrale.
Une fois que nous avons la dérivée, il est facile de déterminer les variations de la fonction. Dans cet exemple, étant donné que sin³(x) a le même signe que sin(x) sur l'intervalle [0, pi], nous savons que la fonction est croissante puis décroissante. Nous pourrions également calculer les valeurs en 0, pi et pi, mais cela n'est pas nécessaire pour déterminer les variations.
En conclusion, il est assez simple de calculer les variations d'une fonction définie comme une intégrale en utilisant la dérivée de cette intégrale. Si vous avez des questions supplémentaires, vous pouvez les poser dans la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

Linéarité d'une Intégrale
Dans cette vidéo, nous utilisons la linéarité de l'intégrale pour simplifier le calcul des primitives en séparant les termes. Nous étudions une fonction f(x) = x^x et devons montrer que la fonction F proposée est une primitive de cette fonction. En dérivant F, nous constatons que nous obtenons bien f(x), ce qui confirme qu'il s'agit d'une primitive.
Ensuite, nous devons calculer l'intégrale de 0 à 1 de 3t - 2 e^x^x. Cependant, il y a une erreur dans l'énoncé où "t" est utilisé à la place de "x". Nous rectifions cette erreur et simplifions l'intégrale en utilisant la méthode de l'intégration par parties (IPP). Nous posons U(x) = 3x - 2 et V'(x) = e^x^x. Nous calculons ensuite les dérivées et primitives de ces termes.
En appliquant l'IPP, nous obtenons une expression simplifiée pour l'intégrale où il ne reste plus qu'à calculer l'intégrale de e^2x. Finalement, nous effectuons les calculs nécessaires et trouvons que l'intégrale équivaut à 2e^5.
En résumé, nous utilisons la linéarité de l'intégrale et la méthode de l'IPP pour calculer la primitive d'une fonction et résoudre une intégrale spécifique. Il est important de garder en tête que lorsque nous avons un polynôme multiplié par une exponentielle, l'IPP est souvent une bonne méthode à employer.
Maths SM&SP
Analyse
2BAC SM Maroc

Encadrer une Intégrale
Dans ce cours, nous abordons la méthode des encadrements d'intégrales pour trouver des limites. Nous commençons par étudier une fonction f(x) égale à E(-x^2). Nous cherchons à encadrer cette fonction pour tout x supérieur à 1. Étant donné que l'exponentielle est toujours positive, nous pouvons dire que E(-x^2) est positive pour tout x supérieur à 1.
Ensuite, nous voulons montrer que cette fonction est inférieure à E(-x). Pour cela, nous utilisons des étapes de raisonnement. Comme x est supérieur à 1, nous multiplions par x (qui est positif) des deux côtés de l'inégalité. Ensuite, nous multiplions par -1 pour changer le signe de x^2, ce qui donne -x^2. Nous composons ensuite cette expression avec l'exponentielle, qui est une fonction strictement croissante et qui ne change pas le signe des inégalités. Ainsi, nous obtenons l'inégalité recherchée.
En utilisant la propriété de monotonie de l'intégrale, nous déduisons un encadrement de l'intégrale de f(x) de 1 à 2. Pour tout x appartenant à l'intervalle [1, 2], nous avons que 0 est inférieur à f(x) qui est inférieur à E(-x). Nous calculons ensuite l'intégrale de ces deux fonctions : l'intégrale de 0 est évidemment 0, et l'intégrale de E(-x) est facilement primitivable et donne E(-1) - E(-2). Ainsi, nous avons encadré notre intégrale entre 0 et E(-1) - E(-2).
C'est ainsi que nous pouvons encadrer une intégrale en utilisant la propriété de monotonie de l'intégrale.
Maths SM&SP
Analyse
2BAC SM Maroc
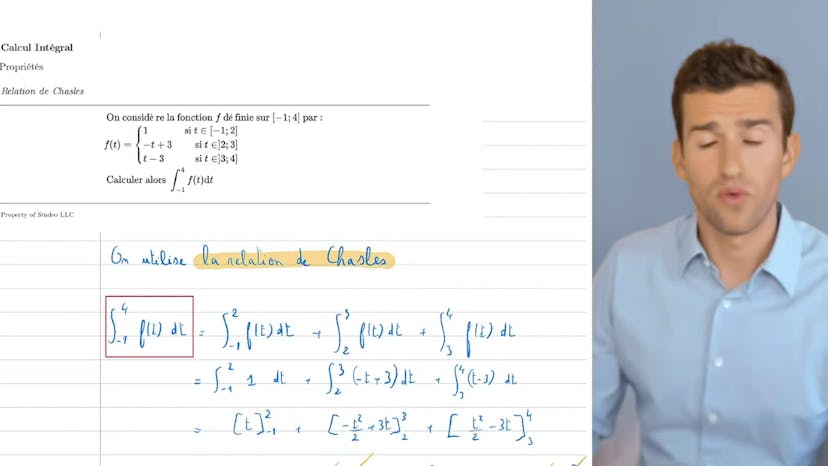
Relation de Chasles
Dans cette leçon, nous apprenons comment utiliser la relation de Schall pour calculer une intégrale. La relation de Schall est simple à utiliser. Nous considérons une fonction f qui a différentes expressions selon l'intervalle. Elle vaut 1 entre (-1,2), elle vaut -t+3 entre 2 et 3, et elle vaut t-3 entre 3 et 4. On nous demande de calculer l'intégrale de (-1,4).
Nous utilisons donc la relation de Schall et disons que l'intégrale de (-1,4) est égale à l'intégrale de (-1,2), plus l'intégrale de 2 à 3, plus l'intégrale de 3 à 4. Nous utilisons les expressions de la fonction dans chaque cas, ce qui est assez simple car ce sont des fonctions usuelles et faciles à primitiver.
L'antidérivée de 1 est t, l'antidérivée de -t+3 est -t²/2+3t, et l'antidérivée de t-3 est t²/2-3t. Nous effectuons les calculs et obtenons 3-4-4, ce qui donne 5 au total. Nous pouvons donc jouer avec les vecteurs et couper l'intégrale en plusieurs morceaux. L'important est de faire attention à ce que les chiffres correspondent, afin que tout se rejoigne correctement.
L'application de la relation de Schall est assez simple, tant que nous faisons attention à ces détails. Nous pouvons choisir librement le point de départ et le point d'arrivée de l'intégrale tant que nous respectons ces conditions. C'est une méthode qui peut être appliquée facilement si nous faisons attention à ces points.


