Cours de Primitives&Équations Différentielles en Ligne par les Meilleurs Professeurs - Primitives&Équations Différentielles

Introduction ED

Une équation différentielle est une équation dont l'inconnue est une fonction. Les équations différentielles sont utilisées en physique pour modéliser des phénomènes tels que le mouvement d'un objet ou la variation de température. Par exemple, lorsque l'on tire un boulet de canon, sa vitesse dépend de sa position. La vitesse étant une dérivée de la position, cela donne une équation différentielle. De même, la loi de refroidissement de Newton stipule que la vitesse de refroidissement d'un objet dépend de l'écart entre sa température et la température ambiante, ce qui peut également être modélisé par une équation différentielle. Il existe différents types d'équations différentielles, tels que les équations homogènes et les équations linéaires. Les méthodes de résolution incluent la recherche de solutions particulières ainsi que l'ajout d'une fonction arbitraire dans la solution générale. En conclusion, les équations différentielles sont largement utilisées en physique pour modéliser des phénomènes variables dans le temps.

ED : définitions de base

Le cours traite des équations différentielles homogènes. Ces équations sont de la forme y' = ay, avec a étant un réel non nul. Les solutions de ces équations peuvent toujours s'écrire sous la forme k fois exponentielle à x, avec k étant une constante. Il y a donc une infinité de solutions pour ces équations. Cependant, lorsqu'on fixe une condition initiale, c'est-à-dire une valeur de y à un certain point x0, il n'y a qu'une seule fonction solution qui correspond à cette condition initiale. Il est intéressant de noter que cette fonction solution ressemble à l'exponentielle, ce qui était attendu car l'équation ressemble à la définition de l'exponentielle. Le cours explique ensuite une démonstration de cette propriété des équations homogènes. On commence par faire une démonstration formelle, mais le professeur souhaite montrer l'intuition derrière cette démonstration. Il utilise une approche "physicienne" qui consiste à ignorer certains détails techniques pour trouver une piste de résolution. Il parvient ainsi à montrer que les fonctions solutions sont de la forme exponentielle à x. Cette approche peut sembler choquante en mathématiques, mais elle peut être utilisée pour trouver des pistes de résolution avant de revenir à une démonstration rigoureuse. En utilisant cette intuition, le professeur parvient à poser une nouvelle fonction g(x) qui permet de simplifier la démonstration. Il montre ensuite que la dérivée de g(x) est nulle, ce qui prouve que g(x) est constante. En utilisant cette constante, on peut démontrer que les solutions de l'équation homogène sont bien de la forme exponentielle à x. En conclusion, le cours explique comment les équations différentielles homogènes sont intrinsèquement liées aux fonctions exponentielles, et donne une démonstration de cette propriété en utilisant une approche intuitive.

Solutions Particulières

Les équations différentielles non homogènes sont de la forme Y' = AY + F, où A et F sont des constantes quelconques. La solution de cette équation consiste en la somme d'une solution homogène (Y' = AY) et d'une solution particulière (U' = AU + F). L'ensemble des solutions est donc donné par U + V, avec U solution particulière et V solution homogène. Dans la plupart des cas, on cherche U en s'inspirant de la fonction F. Par exemple, si F est linéaire (3X + 2), on cherche une solution affine (AX + B), et si F est quadratique, on cherche une solution quadratique (AX² + BX + C). On peut appliquer cette méthode de manière systématique, en posant U de la même famille que F. Pour les équations non homogènes avec une fonction constante, la solution particulière est simplement U = -B/1. Cette solution constante est ensuite added to the general solution. Il est important de bien comprendre cette méthode pour résoudre les exercices.

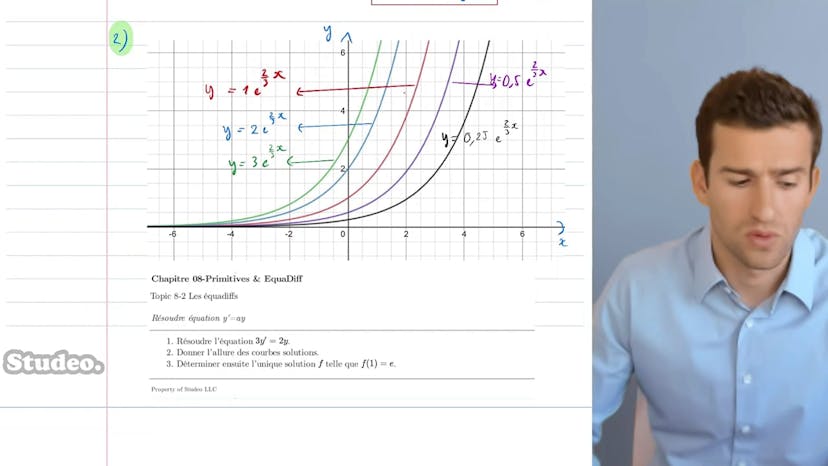
Équation y'=ay

Dans cette méthode, on apprend à résoudre une équation différentielle de premier ordre à coefficient constant, c'est-à-dire une équation du type y' = y. On commence par étudier l'équation différentielle 3y' = 2y en la divisant par 3 pour obtenir y' = (2/3)y. On reconnaît alors la forme y' = y, avec a = 2/3. D'après le cours, on sait que les solutions de cette équation sont de la forme k * e^(ax), soit k * e^(2/3*x) où k est une constante réelle. Ensuite, on nous demande de tracer les courbes solutions de cette équation, en variant la constante k. Plus k augmente, plus la courbe se décolle de l'axe des x, car il s'agit d'une exponentielle avec une constante multiplicative. Toutes les courbes ont donc la même allure. Enfin, on nous demande de trouver la courbe parmi celles-ci qui vérifie f(1) = e. On sait que, pour une équation différentielle avec une condition particulière, il existe une unique solution qui satisfait à la fois l'équation différentielle et la condition particulière. Ici, on veut que f(1) = e, ce qui nous permet de trouver la valeur de k. On suppose que f(x) est de la forme k * e^(2/3*x), on évalue cette expression en x = 1 et on obtient k * e^(2/3) = e. Après résolution, on trouve k = e^(1/3). Donc, la solution recherchée est f(x) = e^(1/3) * e^(2/3*x). C'est une méthode classique pour résoudre une équation différentielle du type y' = y avec une condition initiale. Si vous avez d'autres questions, vous pouvez consulter la FAQ.

Équation y'=ay+b

Aujourd'hui, nous allons voir comment résoudre des équations différentielles d'ordre 1 avec un second membre, c'est-à-dire des équations de la forme y' = y + b, où b est une constante donnée. La méthode est assez simple. Tout d'abord, nous cherchons une solution particulière constante. Ensuite, nous résolvons l'équation homogène, y' = y. En ajoutant ces deux solutions, nous obtenons la solution générale de l'équation. Prenons un exemple : y' = -y + 3. Dans cet exemple, nous résolvons d'abord l'équation homogène y' = -y, ce qui nous donne les solutions de la forme y(x) = ae^(-x), où a est une constante réelle. Ensuite, nous cherchons une solution particulière constante qui satisfait l'équation y' = -y + 3. En trouvant que phi(x) = 3 est une solution, nous ajoutons cette solution à la solution homogène. Ainsi, toutes les solutions de cette équation différentielle sont de la forme y(x) = e^(-x) + 3a, où a est une constante. Pour trouver la valeur de a, on peut utiliser une condition particulière, par exemple y(alpha) = beta. C'est ainsi que l'on résout une équation différentielle du type y' = y + b. N'hésitez pas à poser vos questions dans la description.

Équation y'=ay+φ

Dans ce cours, nous apprenons comment résoudre une équation différentielle de la forme y' = y + phi. Comparé à l'équation y' = y + b, la différence entre b et phi est que b est une constante tandis que phi est une fonction qui peut varier. Cela rend la résolution un peu plus complexe pour trouver la solution particulière. La méthode générale de résolution reste la même : nous devons d'abord trouver une solution particulière en résolvant l'équation sans l'équation homogène (y' = y), puis nous ajoutons la solution homogène. La différence ici est que nous ne cherchons pas une solution particulière sous forme constante. Pour cela, nous avons besoin d'un petit indice fourni dans l'énoncé. Dans cet exemple, on nous demande de vérifier que la fonction p(x) est une solution de l'équation 2. Nous prenons p(x) comme un polynôme, calculons sa dérivée et vérifions si 2p'(x) + 6p(x) est égal à x^2 + 2x - 1. Après les calculs, nous constatons que p(x) est bien une solution. Ensuite, on nous demande de montrer que si f est une solution de l'équation E, cela équivaut à dire que f - p est une solution de l'équation E'. Nous remplaçons x^2 + 2x - 1 par 2p'(x) + 6p(x) dans l'équation pour montrer cette équivalence. En factorisant, nous obtenons 2f'(x) - 2p'(x) + 6f(x) - 6p(x) = 0. De là, nous obtenons que f - p est une solution de l'équation E', où E' est l'équation homogène. Nous résolvons ensuite l'équation E', qui est une équation différentielle que nous connaissons bien : linéaire à coefficient constant de premier ordre sans seconde membre. Nous l'isolons pour obtenir Y' = -3y et reconnaissons une forme de type Y' = Y avec A = -3. En utilisant ce que nous avons dit précédemment sur f - p, nous isolons f sous la forme A*e^(-3x) + p(x). Finalement, nous trouvons que f est de la forme A*e^(-3x) + (1/6)*x^2 + (2/9)*x - 13/54. Nous remarquons qu'il y a toujours une constante de multiplication inconnue. Pour la trouver, nous aurions besoin de conditions particulières dans la fonction, que nous ne possédons pas ici. Cependant, nous pouvons conclure que les fonctions de la forme A*e^(-3x) + (1/6)*x^2 + (2/9)*x - 13/54 sont toutes des solutions de l'équation différentielle. Cela résume le cours sur la résolution des équations différentielles du type y' = y + phi, où phi est une fonction non constante.

Second membre en exponentielle

Les équations différentielles sont importantes dans les études d'ingénieur. Pour une équation du premier ordre du type Y' + Ay = Phi(X), la solution se divise en deux parties. La première partie est la solution sans second membre, qui est généralement l'exponentielle de -AX. La deuxième partie est la solution particulière, qui dépend de la nature de Phi(X). Par exemple, si Phi(X) est une fonction X^2, la solution sera une fonction en X^2. Si Phi(X) est exponentielle 8X, la solution particulière sera de la forme K * exponentielle 8X. Si Phi(X) est une somme de termes, on peut séparer la solution en plusieurs problèmes. Par exemple, si on a X^2 + log(X), on peut trouver une solution sans second membre pour X^2 et une solution sans second membre pour log(X). En résumé, pour résoudre une équation différentielle du premier ordre, on cherche d'abord une solution sans second membre et une solution particulière en fonction de la nature de Phi(X). Ensuite, on peut combiner ces solutions pour obtenir l'ensemble des solutions possibles.

Solution particulière : trigonométrie

Dans ce cours, nous examinons l'équation différentielle donnée et cherchons une solution particulière. Une forme possible est suggérée, mais après une tentative infructueuse, nous réalisons qu'il est préférable d'utiliser à la fois le cos et le sin. Nous identifions ensuite les termes en cos et en sin dans l'équation pour obtenir 0 sin, moins un cinquième cos x et plus deux cinquièmes sin x. En utilisant ces termes, nous formons l'expression y' - 1/2 y = 1/2 cos x. Ainsi, la solution générale de l'équation différentielle est donnée par y(x) = (1/2)e^(x/2)K + g(x), où K est une constante et g(x) est une fonction quelconque. Cette solution générale est obtenue en combinant la solution particulière et la solution sans second membre de l'équation. En conclusion, le principe de résolution des équations différentielles est appliqué, avec une difficulté accrue lors de la recherche de la solution particulière dans des exercices plus avancés.

Solution particulière plus difficile

Dans ce cours, nous examinons comment résoudre l'équation différentielle y'-2y = xe^2x de manière SEO conviviale. Nous commençons par observer que l'expression xe^2x ressemble à un produit entre x et e^2x. Nous essayons donc de trouver une solution particulière de la forme ax + b. Cependant, nous réalisons que cette tentative peut échouer car l'expression ne correspond pas exactement à ce que nous avons identifié. Ensuite, nous envisageons une autre possibilité en utilisant une fonction quadratique g(x) = ax^2 + bx + c. Si notre tentative précédente a échoué, nous essayons cette fois-ci une fonction quadratique. Nous expliquons pourquoi cela peut être nécessaire en utilisant notre expérience : lorsque l'équation à résoudre est égale à zéro et a une solution du type e^2x, nous constatons que généralement, nous devons augmenter le degré de la fonction pour trouver une solution. C'est pourquoi nous ne pouvons pas trouver une fonction g(x) qui satisferait l'équation. Nous encourageons les étudiants à ne pas paniquer lorsqu'ils sont confrontés à ce genre de situation. L'étape suivante consiste simplement à réessayer avec une fonction polynomiale de degré 2. Dans notre cas, nous choisissons g(x) = ax^2 + bx + c et constatons que certains termes disparaissent lors de la résolution. Cela est facilement compréhensible si l'on se rappelle que le terme x^2 dans g(x) disparaissait lors de la tentative précédente avec une fonction plus simple. La valeur de c n'affecte pas la solution, nous choisissons donc c = 0 pour simplifier nos calculs. Ainsi, nous trouvons une solution g(x) qui est approximativement de degré 2 fois l'exponentielle de 2x. La solution générale est alors donnée par y(x) = k*e^(2x) + (x^2/2)*e^(2x), où k est une constante réelle qui variera en fonction des conditions initiales. En forme réduite, nous avons y(x) = (k + x^2/2)*e^(2x). Il est important de noter que la forme réduite de la solution permet une interprétation plus intuitive des termes constants et exponentiels. Veillez également à adapter cette solution en fonction du contexte et des conditions initiales spécifiques.