 All subjects
All subjects
 All subjects
All subjects
Maths Spé
Analyse
Terminale

Intro Suites et limites
Lors de cette vidéo sur les limites de suite, le professeur explique que les définitions formelles peuvent paraître moches et effrayantes, mais qu'elles sont nécessaires pour obtenir des prédictions précises. Il suggère de toujours se référer aux dessins qui accompagnent les formules, pour mieux les comprendre. À cet égard, les limites de suite ont des similitudes avec l'étude des dérivées, où les tables de dérivées classiques ont remplacé les calculs fastidieux de taux d'accroissement. Dans le cas des limites de suite, il y a des tableaux de limites classiques à connaître par cœur. Le cours est divisé en trois parties principales: la définition des limites en infini, en moins infini, et en un point L réel, la présentation des limites de référence et des opérations sur les limites, et enfin une section bonus sur les limites des suites géométriques. Les principales méthodes d'étude incluent l'application de la définition formelle dans les exercices, l'utilisation des limites de référence et des opérations pour prédire les limites, la résolution de cas plus compliqués, et un rappel sur la somme des termes d'une suite géométrique.
Maths Spé
Analyse
Terminale

Limite avec A ou Ɛ
Dans ce cours, on explique la définition mathématique d'une limite en mathématiques. L'objectif est de trouver le plus petit entier n0 tel que, pour toutes les valeurs de la suite au-delà de ce rang, elles soient supérieures à un certain réel a. Cela signifie que même si le réel a est très grand, il existe un rang à partir duquel toutes les valeurs de la suite seront supérieures à a. Pour trouver n0, on résout une équation et utilise la partie entière du résultat pour s'assurer que n0 est un nombre entier. La définition complète de la limite est illustrée par un exemple de suite qui tend vers l'infini. Bien que les définitions formelles puissent sembler difficiles, elles sont importantes pour comprendre les limites en mathématiques.
Maths Spé
Analyse
Terminale

Forme indéterminée 1 : factoriser par terme de plus haut degré
Dans ce cours, nous allons étudier les méthodes pour calculer des limites indéterminées. Nous commençons avec le cas des polynômes en n, où le terme de plus haut degré est le seul à compter. Nous le démontrons en factorisant par le terme de plus haut degré et en observant le comportement de la fraction obtenue. Si nous avons un terme de plus l'infini fois un coefficient, nous obtenons une limite qui tend vers plus l'infini. Ainsi, la factorisation par le terme de plus haut degré nous permet de déterminer le coefficient dominant qui va imposer la limite. Cette méthode fonctionne pour tous les polynômes.
Maths Spé
Analyse
Terminale

Forme indéterminée 2 : la quantité conjuguée
Ce cours aborde les méthodes pour une fonction rationnelle, qui est un polynôme divisé par un autre polynôme. Pour résoudre la fonction, il faut factoriser par le terme de plus haut degré pour trouver quel terme l'emporte. Il y a trois cas de figure : lorsque le degré de P est strictement supérieur à celui de Q, lorsque le degré de Q est strictement supérieur à celui de P, ou lorsque les deux sont de la même force. Dans ce dernier cas, la limite tend vers le rapport des coefficients dominants de P et Q. Les n se simplifient en partie et l'on peut trouver la solution optimale pour la fonction.
Maths Spé
Analyse
Terminale

Limite d'une somme géométrique
En bref, pour calculer une somme limitée, il faut d'abord vérifier si les termes de la somme correspondent à une suite arithmétique ou géométrique connue. Si c'est le cas, on peut utiliser une formule adaptée pour calculer la somme. Dans cet exemple, les termes correspondent à une suite géométrique, ce qui permet d'appliquer la formule de la somme des termes consécutifs d'une suite géométrique. Après quelques vérifications, on trouve que la somme tend vers l'infini.
Maths Spé
Analyse
Terminale

Trouver à la calculette "le plus petit entier tel que..."
Dans ce cours, nous étudions une suite en cherchant le plus petit entier tel que le terme de la suite soit supérieur à une certaine valeur. La suite a0=2 et la relation de récurrence est an+1=3an. Nous voyons que la suite augmente très vite. Nous utilisons ensuite un petit programme pour trouver le premier entier n tel que an>1000. Le programme utilise une boucle "tant que" pour calculer les termes de la suite jusqu'à ce que celui-ci dépasse 1000. Nous affichons ensuite la valeur de n pour connaître à quel rang nous sommes. Nous pouvons également calculer cela par itération sans programme. Le premier entier n tel que an>1000 est 6. Cette méthode peut être utile pour résoudre d'autres problèmes similaires.
Maths Spé
Analyse
Terminale
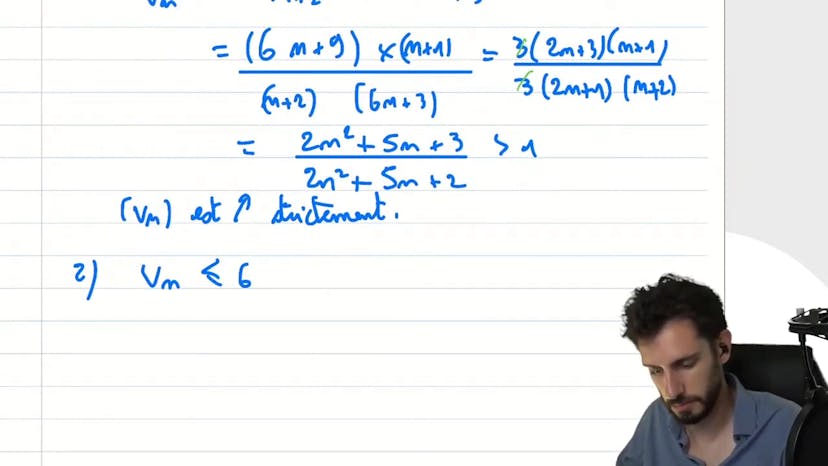
Suite-fraction
La vidéo parle de la convergence d'une suite donnée par vn = 6n+3 / (n+1). Pour étudier les variations, le professeur utilise le critère de croissance en comparant vn+1 / vn à 1. Après des calculs, il montre que ce ratio est strictement supérieur à 1, ce qui implique que la suite vn est strictement croissante. Ensuite, il montre que la suite est majorée par 6 en montrant que vn+3 égale à 6 pour tout n. Enfin, il applique le théorème de convergence monotone pour conclure que la suite vn converge. Le professeur propose également une méthode alternative où il simplifie l'expression de vn en écrivant vn = 6(n+1) - 3 / (n+1), permettant ainsi d'étudier les variations plus facilement. Il conclut en disant que la limite de la suite vn est égale à 6.
Maths Spé
Analyse
Terminale

Plein de limites !
Dans ce cours sur les limites en mathématiques, nous apprenons deux méthodes principales pour les gérer : la méthode du terme dominant et la méthode de l'encadrement. La première consiste à comparer les termes dominants au numérateur et au dénominateur d'une fraction pour avoir une intuition de ce qui se passera lorsque n devient très grand. La seconde méthode nous permet d'utiliser le théorème d'encadrement en encadrant les éléments dans une question sur les limites de suite contenant des fonctions trigonométriques. Le cours nous enseigne comment factoriser le terme dominant pour répondre à la question en haut et en bas, et comment utiliser le théorème des gendarmes pour des limites finies encadrées des deux côtés. Des exemples sont donnés pour illustrer les méthodes, et nous apprenons également comment utiliser la comparaison de puissance pour répondre aux limites géométriques.
Maths Spé
Analyse
Terminale

Téléscopage !
Le cours traite de la détermination de limites de suites définies comme des sommes de termes d'autres suites. Le premier exercice consiste à déterminer la limite de la suite Un, qui est 1/n, qui tend vers 0. Ensuite, l'exercice suivant montre que pour toutes les n appartenant à N, Un égale à 1/(n-1) - 1/n+1. La difficulté de cet exercice est de ne pas recopier la réponse et de partir de l'équation donnée pour démontrer qu'elle est égale à Un. Le troisième exercice consiste à calculer la somme de la suite. En utilisant la question précédente, on peut simplifier l'expression de Un en une somme télescopique, où les termes successifs se dégagent mutuellement, laissant seulement Un et Un+1. Finalement, on obtient que la somme tend vers 1.
Maths Spé
Analyse
Terminale

Majoration astucieuse
Le cours concerne l'étude des variations et la convergence d'une suite mathématique donnée sous la forme d'un quotient, Vn = (6n + 3)/(n + 1). La méthode classique consiste à utiliser le critère de croissance en comparant Vn+1/Vn à 1 pour montrer que la suite est croissante et à démontrer qu'elle est bornée par 6 pour déduire qu'elle converge grâce au théorème de convergence monotone. Une autre méthode consiste à travailler sur l'expression de Vn en écrivant Vn = (6n + 1 - 3)/(n + 1) = ((6n + 1)/(n + 1)) - (3/(n + 1)) pour montrer que la suite est croissante et bornée par 6, et pour obtenir directement la limite de la suite qui est 6. L'analyse mathématique de cette suite est utilisée pour illustrer différentes méthodes et stratégies de résolution de problèmes en mathématiques.
Maths Spé
Analyse
Terminale
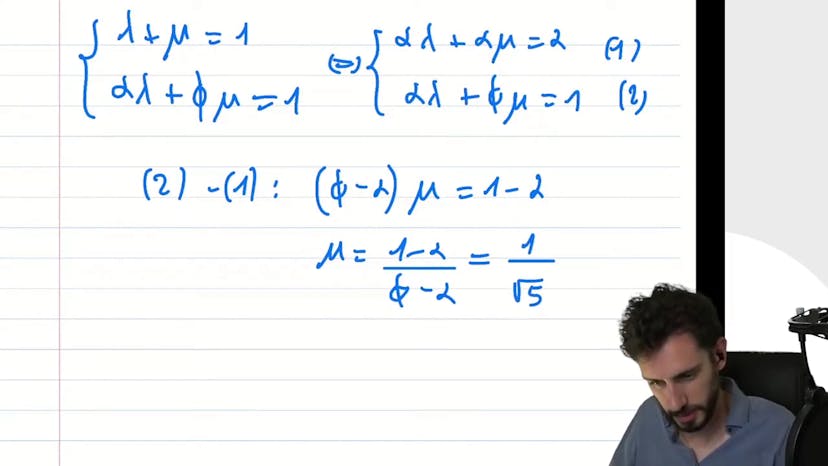
Prépa : Fibonacci
La suite de Fibonacci et le nombre d'or sont définis par récurrence avec chaque terme étant la somme des deux précédents. Pour exprimer chaque terme de la suite comme une combinaison linéaire de sommes géométriques, il faut trouver des réels a, b, lambda et mu qui vérifient une certaine relation de récurrence. Au lieu de résoudre directement les équations impliquant les quatre variables, on peut chercher s'il existe uniquement une somme géométrique qui fonctionne, ce qui mène à deux valeurs potentielles pour la raison de la suite géométrique. En utilisant cela, on peut aboutir à une expression simple pour chaque terme de la suite de Fibonacci en fonction du nombre d'or et de certains coefficients. En analysant les raisons de la suite géométrique, on peut montrer que la suite de Fibonacci converge vers le nombre d'or.
Maths Spé
Analyse
Terminale

Limite finie
Dans cette vidéo, nous abordons la notion de limite réelle en mathématiques. La limite réelle est la valeur vers laquelle une suite converge intuitivement lorsque n augmente. Pour être plus précis, nous utilisons la notion de couloir. Dans cette vidéo, nous expliquons ce qu'est un couloir autour de la limite et montrons qu'une suite peut converger de manière douce (croissance ou décroissance) ou chaotique.
Officiellement, on dit qu'une suite UN converge vers un réel L si tout intervalle autour de L (incluant L) finit par contenir tous les termes de la suite à un certain moment. Pour illustrer cela graphiquement, nous utilisons un graphique représentant la suite et un couloir de taille variable autour de la limite (2 dans cet exemple). Nous vérifions si tous les termes de la suite sont inclus dans le couloir à partir d'un certain moment. Si cela est vrai pour toutes les tailles de couloir, alors la limite est valide.
Nous illustrons ensuite cette idée en réduisant la taille du couloir de plus en plus. Si tous les termes de la suite sont inclus dans le couloir à partir d'un certain moment, cela signifie que les termes de la suite se rapprochent de plus en plus de la limite (2 dans cet exemple), indépendamment de la taille du couloir. Nous démontrons également que cette notion de convergence peut s'appliquer à des suites croissantes, décroissantes ou oscillantes autour de la limite.
En résumé, cette vidéo explique la notion de limite réelle en mathématiques en utilisant la notion de couloir pour illustrer graphiquement cette idée. Nous montrons également que les suites peuvent converger de différentes manières vers leur limite, que ce soit de manière croissante, décroissante ou oscillante.
Maths Spé
Analyse
Terminale

En l'infini
Dans ce cours, l'auteur explique ce qu'est une limite infinie. Une suite tend vers plus l'infini si tous ses termes sont supérieurs à n'importe quel plateau fixé. L'auteur illustre cela avec un graphique d'une suite croissante basée sur la parabole X2. Peu importe la valeur du plateau choisie, on peut toujours trouver un rang à partir duquel tous les termes de la suite dépassent ce plateau. Cette propriété est appelée " tendre vers plus l'infini ".
Ensuite, l'auteur aborde la limite en moins l'infini. Il explique qu'une suite décroissante peut tendre vers moins l'infini si tous ses termes sont inférieurs à n'importe quel plateau fixé. À l'aide d'un graphique, il montre que peu importe la valeur du plateau choisie, il existe un rang à partir duquel tous les termes de la suite sont inférieurs à ce plateau. Cette propriété est appelée " tendre vers moins l'infini ".
L'auteur souligne que ces définitions sont symétriques et doivent être comprises pour pouvoir les utiliser dans des exercices ou des méthodes plus avancées. Il encourage également les étudiants à poser des questions s'ils ont des doutes et annonce la prochaine vidéo.
Maths Spé
Analyse
Terminale
Unicité et Divergence
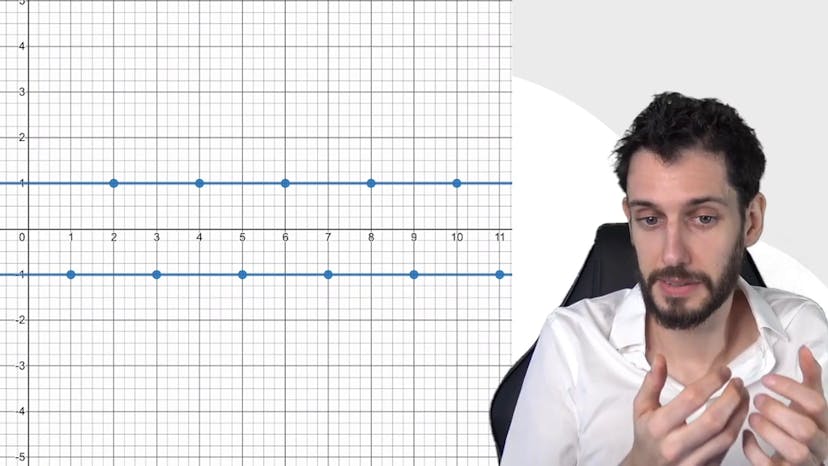
La convergence se réfère à la limite finie d'une suite. Lorsque vous avez une limite finie, elle est unique, ce qui signifie qu'une suite ne peut tendre vers deux valeurs différentes. Cependant, il est important de noter que le fait d'être divergent, c'est-à-dire de ne pas être convergent, ne signifie pas nécessairement tendre vers l'infini positif ou négatif. Il existe des cas où une suite peut osciller sans tendre vers une limite finie. Par exemple, la suite (-1)^(n) oscille entre -1 et 1 sans converger vers l'un ou l'autre. Bien que certains termes de la suite puissent sembler converger vers 1 ou -1, dans son ensemble, cette suite n'a pas de limite. Il est possible d'extraire des sous-suites pour lesquelles la convergence est observable, mais cela dépasse le cadre du programme scolaire. En résumé, la convergence d'une suite vers une limite finie est unique, mais il est également possible d'avoir des suites divergentes qui n'oscillent pas vers l'infini. Si vous avez besoin de plus de détails, n'hésitez pas à consulter la FAQ ou à discuter avec nous. À bientôt !
Maths Spé
Analyse
Terminale

Limites de référence et opérations
Ce cours traite de la convergence et de la divergence des suites. Il aborde les outils pratiques à connaître tels que les puissances de n qui tendent vers l'infini, les puissances négatives de n qui tendent vers zéro, et les opérations sur différentes suites. Il est important de connaître les formes indéterminées, qui sont des cas où il n'y a pas de règle prédéterminée et qui nécessitent une approche cas par cas. Les formes indéterminées comprennent la somme, le produit et le quotient de deux suites qui tendent respectivement vers l'infini, zéro et l'infini ou zéro. Il est essentiel de mémoriser ces formes indéterminées et de les appliquer dans les exercices. En résumé, il est recommandé d'apprendre les tables par cœur et de se familiariser avec les différentes formes indéterminées.
Maths Spé
Analyse
Terminale
Suites géométriques - illustration
Dans cette vidéo, nous abordons le sujet des suites géométriques et leurs différents comportements en fonction de la valeur de la raison (Q).
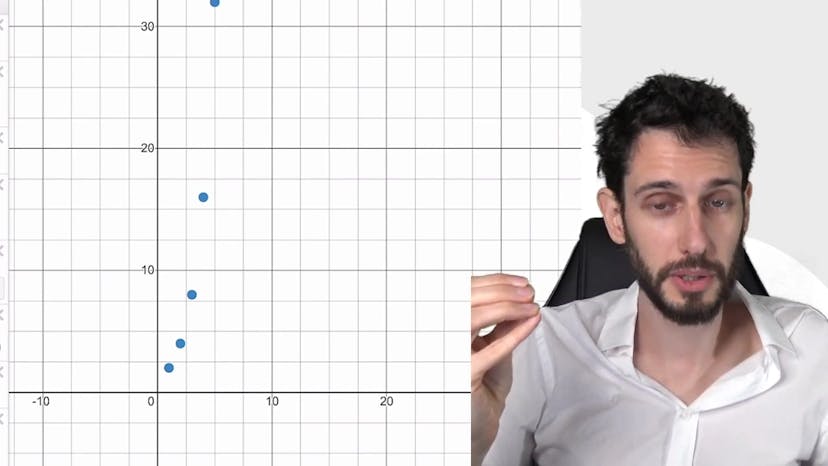
Tout d'abord, lorsque Q est supérieur à 1, on nous dit que Q à la puissance n tend vers l'infini. Cela est illustré en prenant l'exemple de Q égal à 3, où chaque terme de la suite augmente de plus en plus. Ce comportement peut être démontré à l'aide de l'inégalité de Bernoulli.
Ensuite, lorsqu'on a une raison entre -1 et 1 (pour le cas positif), on observe que la suite se rapproche de plus en plus de zéro. Par exemple, avec Q égal à 0,5, chaque terme de la suite diminue de moitié à chaque étape, et finit par converger vers zéro. Ce comportement est intuitive, car on enlève un petit bout à chaque fois.
Pour le cas négatif, où Q est strictement inférieur à -1, on observe un comportement plus complexe. La suite oscille entre des valeurs positives et négatives, mais converge tout de même vers zéro. Par exemple, avec Q égal à -0,7, on voit que certains termes sont positifs tandis que d'autres sont négatifs, mais l'ensemble de la suite se rapproche de zéro.
Finalement, le cas où Q est égal à 1 est trivial, car tous les termes de la suite sont égaux à 1.
En résumé, lorsque la raison est proche de zéro (-1 < Q < 1), la suite converge vers zéro, soit en oscillant, soit non. Lorsque la raison est supérieure à 1 ou inférieure à -1, la suite s'écarte de zéro, soit en tendant vers l'infini, soit d'une manière plus complexe en s'écartant des deux côtés à la fois.
Maths Spé
Analyse
Terminale

Suites géométriques : démo
Dans cette vidéo, nous démontrons les intuitions sur la limite des suites géométriques pour plusieurs cas. Si q est plus grand que 1, nous utilisons l'inégalité de Bernoulli et le terrain de comparaison pour montrer que la limite de q puissance n tend vers plus infini. Pour le cas où q est entre 0 et 1, nous posons p égal à 1 sur q et appliquons le résultat précédent pour montrer que p plus s enseigne tend vers plus infini et donc que q plus s enseigne tend vers 0. Enfin, pour le cas où q est entre moins 1 et 0, nous utilisons le théorème des gendarmes pour montrer que q puissance n tend vers 0. La démonstration est à savoir par cœur dans le programme.
Maths SM&SP
Analyse
2BAC SM Maroc

Intro Suites et limites
Bienvenue dans cette vidéo d'introduction sur les limites de suite. Une limite de suite correspond à un point où les valeurs de la suite se rapprochent et semblent atteindre une valeur fixe, appelée plateau. Dans l'exemple donné, on voit une suite qui monte jusqu'à une certaine valeur, puis semble se coller à un plateau autour de la valeur 1. Plus la valeur de n augmente, plus la suite semble être proche de cette limite. Cependant, il faudra utiliser des définitions plus formelles pour être précis en mathématiques. Ces définitions peuvent sembler compliquées, mais il est important de les maîtriser. Un parallèle est fait avec l'étude de la dérivée, où au début on utilisait une définition et des calculs complexes, mais plus tard on a utilisé des tables de dérivées pour simplifier les choses. Pour les limites de suite, il y aura également des définitions formelles, mais aussi des tableaux de limites classiques à connaître. Le cours abordera la définition des limites en l'infini, en moins l'infini et en un point réel, ainsi qu'une propriété d'unicité des limites. Il y aura aussi une partie sur les limites de référence et les opérations possibles avec les limites, avec des tableaux à mémoriser. Enfin, il y aura une partie bonus sur les limites des suites géométriques. En termes de méthode, il y aura quatre approches principales : l'application de la définition formelle, la prédiction des limites grâce aux limites de référence et aux opérations, l'utilisation de techniques supplémentaires dans certains cas plus complexes, et enfin, un rappel sur la somme des termes d'une suite géométrique et les cas où cette somme peut avoir une limite. N'hésitez pas à poser des questions dans la FAQ et je vous retrouve dans la prochaine vidéo.
Maths SM&SP
Analyse
2BAC SM Maroc

Limite finie
La limite réelle est la valeur vers laquelle une suite converge intuitivement lorsque n augmente. En mathématiques, on utilise la notion de couloir pour décrire plus précisément cette idée. Dans cette vidéo, je vais expliquer ce qu'est un couloir autour de la limite et montrer différentes façons de converger vers un réel, que ce soit de manière croissante, décroissante ou chaotique.
La définition officielle de la limite dit que la suite Un converge vers un réel L si tout intervalle autour de L finit par contenir tous les termes de la suite à un certain moment. Pour vérifier cela graphiquement, je prends un couloir autour de la limite supposée. Si tous les termes de la suite sont inclus dans ce couloir à partir d'un certain moment, alors la limite est validée.
Réduire la taille du couloir montre que les termes de la suite peuvent être de plus en plus proches de la limite, quelle que soit la distance choisie. En d'autres termes, on peut toujours se rapprocher autant que l'on souhaite de la limite.
Je présente ensuite quelques exemples de suites qui convergent vers 2, que ce soit de manière croissante, décroissante ou en oscillant. Ces différents cas montrent qu'il existe plusieurs façons de converger vers une limite.
J'invite les spectateurs à poser leurs questions ou demander des précisions dans la FAQ et je termine en annonçant la prochaine vidéo.
En résumé, cette première vidéo sur la définition des limites explique la notion de couloir autour d'une limite réelle et montre différentes façons de converger vers cette limite.
Maths SM&SP
Analyse
2BAC SM Maroc

En l'infini
Une limite infinie signifie que pour n'importe quel plateau donné, une suite tendra à dépasser ce plateau et tous ses termes seront au-dessus de ce plateau. Cela signifie que la suite peut aller toujours plus haut. On peut l'illustrer graphiquement en utilisant une suite croissante basée sur la parabole X2. Peu importe la valeur du plateau choisie, il existe un entier n pour lequel tous les termes de la suite sont au-dessus de ce plateau. Cette idée est appelée "tendre vers plus l'infini". De manière similaire, pour la limite moins l'infini, une suite décroissante peut avoir tous ses termes en dessous d'un plateau donné. Il est important de comprendre graphiquement ces deux propriétés et de les utiliser dans des exercices. Si vous avez des questions, n'hésitez pas à les poser dans la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc
Unicité et divergence
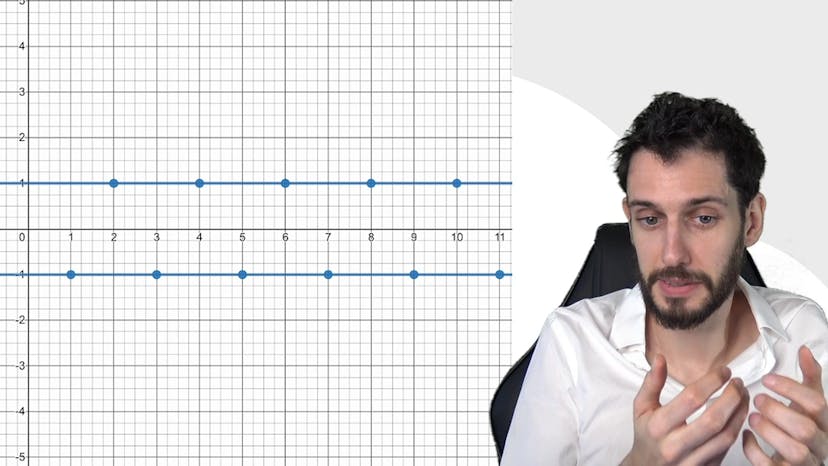
Dans cette vidéo, on aborde la convergence et les limites en mathématiques. Il y a deux points importants à retenir. Le premier est que lorsqu'une limite est finie, elle est unique. En d'autres termes, on ne peut se rapprocher que d'une seule valeur. Le deuxième point concerne le vocabulaire utilisé. On utilise le terme "convergence" pour décrire une suite qui a une limite finie. Cependant, il est important de noter que ne pas être convergent ne signifie pas automatiquement tendre vers l'infini. Il est possible de diverger d'une autre manière.
Un exemple de divergence est donné avec la suite "-1 puissance n". Cette suite oscille entre -1 et 1 et ne tend ni vers l'infini ni vers moins l'infini. On peut dire qu'elle a un comportement d'oscillation permanent. On peut également extraire des sous-suites à partir de cette suite pour observer des convergences partielles, mais dans son ensemble, la suite n'a pas de limite.
En conclusion, il est important de comprendre que la convergence en mathématiques ne se limite pas seulement à tendre vers l'infini ou moins l'infini. Il existe des cas de divergence avec des comportements d'oscillation permanente. Pour plus de détails et d'informations, vous pouvez consulter la FAQ ou discuter avec nous.
Maths SM&SP
Analyse
2BAC SM Maroc

Références et opérations
Lorsque nous étudions la convergence et la divergence de suites vers une limite finie ou infinie, il y a différentes règles et outils à connaître.
Tout d'abord, les puissances de n tendent vers l'infini lorsque n tend vers l'infini. Par exemple, n, n², n³, etc. tendent tous vers l'infini. Il est important de noter que cette règle s'applique également aux puissances non-entières, telles que la racine de n, qui peut être écrite comme n puissance 1,5. En général, les puissances positives de n, quelle que soit la valeur de k (entier ou rationnel), tendent vers l'infini.
De plus, il est important de comprendre que plus la puissance augmente, plus la suite tend vers l'infini rapidement. Par exemple, n³ augmente plus rapidement que n².
En ce qui concerne les puissances négatives de n, c'est-à-dire 1/n, elles tendent toutes vers zéro. En divisant 1 par un nombre très grand, nous obtenons un nombre très petit, proche de zéro.
Ensuite, il est essentiel de savoir comment gérer les opérations sur différentes suites. Par exemple, si nous connaissons les limites de deux suites, pouvons-nous déterminer la limite de leur somme ? Dans la plupart des cas, la réponse est oui. Il existe une règle prédéterminée selon laquelle si une suite tend vers l et une autre vers l', leur somme tend vers l + l'. Si l'une des suites tend vers plus ou moins l'infini et l'autre vers une limite finie, c'est l'infini qui l'emporte. Si les deux suites tendent vers plus ou moins l'infini, leur somme tend également vers plus ou moins l'infini.
Cependant, il existe des situations plus complexes appelées "formes indéterminées", pour lesquelles il n'y a pas de règle prédéterminée. Dans ces cas, il faut analyser la situation au cas par cas. Par exemple, si une suite tend vers l'infini et une autre vers moins l'infini, la somme peut être égale à zéro ou à l'infini, selon les valeurs spécifiques des suites. Il est donc important de comprendre qu'il existe des formes indéterminées et de savoir les reconnaître lorsqu'elles se présentent.
Il y a également des formes indéterminées pour les produits de suites, par exemple lorsque l'une tend vers zéro et l'autre vers l'infini. Il faut faire attention à ces situations et les analyser individuellement.
Pour les quotients de suites, il peut y avoir deux formes indéterminées : plus l'infini sur plus l'infini et zéro sur zéro. Il est donc nécessaire de prêter une attention particulière à ces cas.
En conclusion, il est important de mémoriser les règles et les formes indéterminées associées à la convergence et à la divergence des suites. De plus, il est crucial d'appliquer ces connaissances lors de la résolution d'exercices.
Maths SM&SP
Analyse
2BAC SM Maroc
Suites géométriques - Illustration
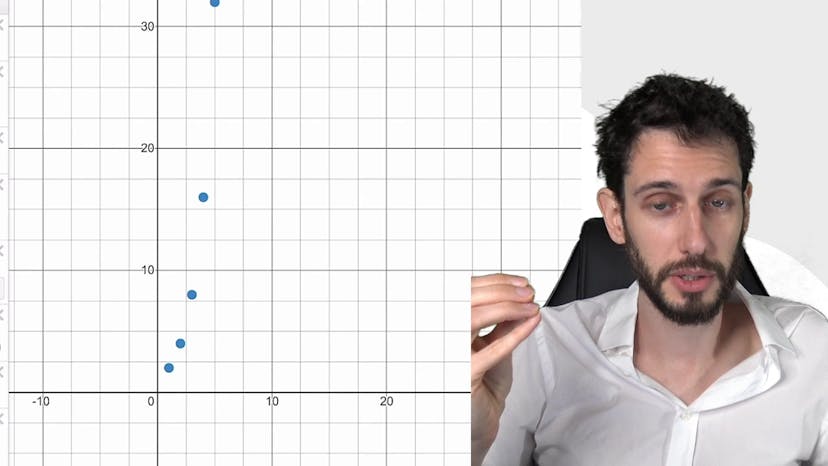
Dans cette vidéo, nous abordons les concepts de convergence et de divergence des suites géométriques. Une suite géométrique est définie par une raison, notée Q, et peut avoir différents comportements en fonction des valeurs de cette raison.
Lorsque Q est strictement supérieur à 1, la suite tend vers l'infini. Par exemple, si nous prenons Q égal à 3, nous obtenons une suite qui augmente rapidement : 3, 9, 27, 81, etc. Ce comportement peut être démontré à l'aide de l'égalité de Bernoulli.
Lorsque Q est compris entre -1 et 1, la suite converge vers zéro. Par exemple, si nous prenons Q égal à 0,5, nous obtenons une suite qui diminue progressivement : 0,5, 0,25, 0,125, etc. L'intuition derrière cela est que la raison Q, plus petite que 1, enlève un petit bout à chaque terme précédent, conduisant finalement à zéro.
Si Q est égal à 1, la suite est constante et égale à 1.
Si Q est inférieur à -1, la suite diverge, mais d'une manière différente. Dans ce cas, la suite ne converge ni vers l'infini ni vers moins l'infini, mais oscille entre des valeurs positives et négatives. Par exemple, si nous prenons Q égal à -0,7, nous obtenons une suite qui oscille autour de zéro sans converger vers une valeur spécifique.
Ces différents comportements peuvent être illustrés graphiquement. Par exemple, la suite 2^n augmente rapidement et converge vers l'infini. Les suites avec une raison entre -1 et 1, comme 0,7^n, diminuent progressivement et convergent vers zéro. Les suites avec une raison inférieure à -1, comme -0,7^n, oscillent autour de zéro sans converger vers une valeur précise.
Il est essentiel de comprendre visuellement ces différents cas afin de saisir les concepts de convergence et de divergence des suites géométriques. Dans la prochaine vidéo, nous aborderons les démonstrations mathématiques de ces comportements.
Maths SM&SP
Analyse
2BAC SM Maroc
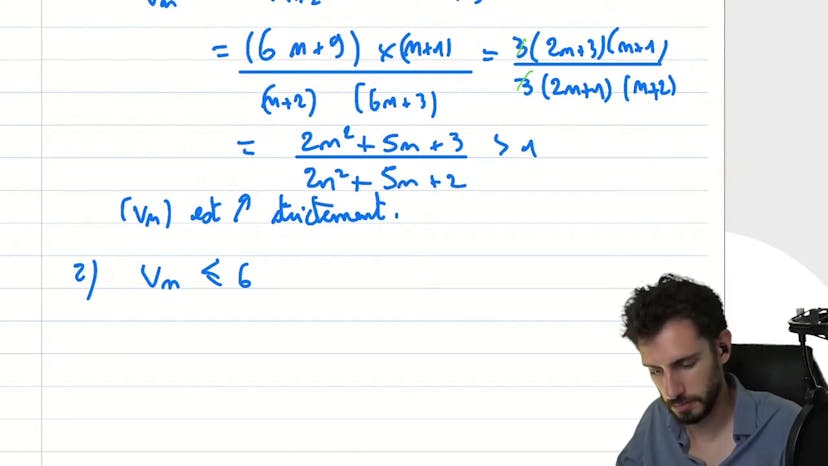
Essai limites
La suite vn = 6n + 3 / n + 1 est étudiée pour déterminer ses variations et sa convergence. Pour cela, deux méthodes sont utilisées.
Méthode 1: Les variations de la suite sont étudiées en utilisant le critère de croissance. On montre que le ratio vn+1 / vn est strictement supérieur à 1, ce qui implique que la suite est croissante. Ensuite, on démontre que la suite est majorée par 6, ce qui permet de conclure que la suite convergente.
Méthode 2: On simplifie l'expression de vn en forçant l'apparition de n+1 au numérateur. On obtient vn = 6n + 3 / n + 1 = (6n + 6 - 3) / (n + 1) = (6(n + 1) - 3) / (n + 1) = 6 - 3 / (n + 1). En analysant cette nouvelle expression, on conclut que la suite est croissante, positivement bornée par 6, et converge vers 6.
En résumé, la suite vn = 6n + 3 / n + 1 est croissante, majorée par 6, et converge vers 6.
Maths SM&SP
Analyse
2BAC SM Maroc

Limite finie
Dans cette vidéo, nous abordons la définition des limites en mathématiques. Une limite réelle est la valeur vers laquelle une séquence tend au fur et à mesure que n augmente. Pour expliquer cette notion, on utilise celle de couloir. Nous présentons deux aspects : tout d'abord, une explication détaillée du concept de couloir entourant la limite, puis nous montrons que la convergence peut se faire de manière régulière (croissante, décroissante) ou plus chaotique (oscillante). La définition officielle stipule qu'une séquence converge vers une limite L si, pour tout intervalle autour de L, tous les termes de la séquence finissent par être compris dans cet intervalle à un certain moment. Sur un graphique, nous observons une séquence donnée entourée d'un couloir représentant la limite. On vérifie que tous les termes de la séquence sont inclus dans le couloir à partir d'un certain point. Si cette propriété est vérifiée pour tous les intervalles, alors L est bien une limite. Nous examinons différents exemples pour illustrer les différentes façons de converger vers une limite : une séquence croissante, une séquence décroissante et une séquence oscillante. Nous soulignons que la notion de couloir permet d'englober ces différentes situations. Cette vidéo fournit un aperçu de la définition des limites et présente des exemples graphiques pour faciliter la compréhension. N'hésitez pas à consulter la FAQ pour poser des questions ou obtenir des éclaircissements. Rejoignez-nous dans la prochaine vidéo pour continuer notre exploration des limites.
Maths SM&SP
Analyse
2BAC SM Maroc

En l'infini
Dans ce cours, nous abordons les limites infinies. On dit qu'une suite "un" tend vers plus l'infini si, pour n'importe quel plateau A, il existe un rang n à partir duquel tous les termes de la suite sont supérieurs à A. Cela signifie que la suite peut dépasser n'importe quel plateau et continuer à croître. Cette idée est illustrée graphiquement avec une suite croissante basée sur la parabole x². On peut constater que pour n'importe quel plateau, comme 8 ou 50, il existe un rang à partir duquel tous les termes de la suite sont au-dessus de ce plateau. Nous appelons cela une limite vers plus l'infini. Pour la limite vers moins l'infini, nous utilisons une suite décroissante, l'inverse de la première. Encore une fois, on peut constater graphiquement que pour n'importe quel plateau, comme -45 ou 60, il existe un rang à partir duquel tous les termes de la suite sont en dessous de ce plateau. Cela signifie que la suite peut passer sous n'importe quel plateau. Nous appelons cela une limite vers moins l'infini. Il est important de comprendre ces concepts graphiques pour pouvoir les utiliser dans des exercices et méthodes classiques. Si vous avez des questions, n'hésitez pas à les poser dans la FAQ.
Maths SM&SP
Analyse
2BAC SM Maroc

Unicité et Divergence
Nous pourrions résumer ce cours sur la convergence en mettant l'accent sur deux points clés. Tout d'abord, une limite finie est unique, ce qui signifie que lorsque nous nous approchons d'une valeur, nous ne pouvons pas nous approcher de deux valeurs différentes. Ensuite, nous devons faire attention à ne pas confondre convergence et tendance vers l'infini ou moins l'infini. Être divergent, c'est-à-dire non convergent, ne signifie pas automatiquement se diriger vers l'infini. Il existe de cas de divergence où les valeurs oscillent sans converger vers une limite finie. Par exemple, une suite telle que (-1)^n oscille entre 1 et -1 sans convergence. Il est important de noter que bien que certains termes de la suite puissent sembler converger vers 1, il n'y a pas de limite globale et la suite ne converge ni vers l'infini, ni vers moins l'infini. Si vous avez besoin de plus de détails, veuillez consulter notre FAQ ou discuter avec nous. À la prochaine !
Maths SM&SP
Analyse
2BAC SM Maroc

Limites de référence et opérations
Lorsque nous examinons les limites finies ou infinies en mathématiques, il est important de connaître certains outils pratiques. Le programme insiste sur le fait que les puissances de "n" tendent vers l'infini lorsque "n" tend vers l'infini. Par exemple, les puissances de "n", telles que "n²" ou "n³", tendent toutes vers l'infini. Il est important de noter que cette règle s'applique non seulement aux puissances entières, mais également aux racines de "n", comme la racine carrée de "n" que l'on peut écrire comme "n" puissance 1,5.
De plus, il est essentiel de comprendre que les puissances de "n" tendent de plus en plus rapidement avec l'augmentation de la puissance. Par exemple, "n³" augmente plus rapidement que "n²".
Un autre outil important concerne les opérations sur différentes suites. Par exemple, si nous connaissons les limites de deux suites, pouvons-nous déterminer directement la limite de leur somme ? Dans la plupart des cas, oui. Il existe une règle prédéterminée selon laquelle si une suite tend vers "l" et une autre tend vers "l'", la somme des deux tendra vers "l + l'".
Il est important de comprendre que lorsque l'une des suites tend vers plus ou moins l'infini et que l'autre tend vers une limite finie, l'infini l'emporte. De même, lorsque les deux suites divergent vers plus ou moins l'infini, leur somme suivra cette tendance. Cependant, lorsqu'il s'agit d'une combinaison spécifique, appelée "forme indéterminée", il n'y a pas de règle prédéterminée. Il est nécessaire d'examiner chaque cas individuellement.
Il existe différentes formes indéterminées, telles que la somme de deux suites tendant vers l'infini et moins l'infini, le produit d'une suite tendant vers zéro et une autre tendant vers l'infini, et le quotient de deux suites tendant vers plus ou moins l'infini ou zéro sur zéro.
Il est crucial de reconnaître ces formes indéterminées et de savoir comment les aborder lorsqu'elles se présentent dans un exercice.
En conclusion, il est recommandé d'apprendre les tables correspondantes, de retenir les règles sur les puissances de "n" et de se familiariser avec les formes indéterminées. En les connaissant et en les comprenant, on sera prêt pour les exercices. N'hésitez pas à consulter les ressources supplémentaires si vous avez des questions ou besoin de précisions.
Maths SM&SP
Analyse
2BAC SM Maroc

Suites géométriques - illustration
Dans cette vidéo, nous explorons la convergence et la divergence des suites géométriques. Une suite géométrique est définie par une raison Q, et selon les valeurs de cette raison, elle peut avoir différents comportements. Nous commençons par illustrer et comprendre intuitivement ces comportements.
Lorsque Q est supérieur à 1, la suite tend vers l'infini. Par exemple, si Q est égal à 3, les termes de la suite augmentent rapidement. Ce comportement peut être démontré avec l'inégalité de Bernoulli.
Lorsque Q est entre -1 et 1, nous prenons l'exemple de Q égal à 0,5. À chaque étape, nous prenons la moitié du terme précédent, et cela continue à l'infini. Nous comprenons intuitivement que lorsque nous prenons un nombre plus petit que 1, nous enlevons un petit bout à chaque fois, ce qui aboutit à 0.
Si Q est égal à 1, tous les termes de la suite sont égaux à 1, donc cela converge vers 1.
Si Q est inférieur à -1, la suite diverge, mais ne tend ni vers l'infini, ni vers moins l'infini. Nous illustrons ce cas avec Q égal à -0,7. Les termes de la suite oscillent mais convergent vers 0.
En résumé, lorsque la raison Q est entre -1 et 1, la suite converge vers 0, soit en oscillant, soit pas. Lorsque la raison Q est supérieure à 1 ou inférieure à -1, la suite s'écarte de 0, soit vers l'infini, soit en s'écartant des deux côtés à la fois avec un terme sur deux.
Cette vidéo donne une illustration visuelle de ces différents cas. La démonstration sera abordée dans une prochaine vidéo.
Maths SM&SP
Analyse
2BAC SM Maroc

Suites géométriques : démo
Dans cette vidéo, nous allons démontrer les intuitions graphiques sur la limite des suites géométriques.
Premièrement, si Q est strictement plus grand que 1, nous allons montrer que Q puissance n tend vers l'infini. Pour cela, nous utilisons l'inégalité de Bernoulli et le terrain de comparaison. Nous écrivons Q égal à 1 plus h, où h est positif. En utilisant l'inégalité de Bernoulli, nous obtenons que 1 plus h puissance n est plus grand ou égal que 1 plus n h. Comme 1 plus n h est une suite arithmétique de raison positive qui tend vers l'infini, nous pouvons conclure que Q puissance n tend vers l'infini.
Ensuite, pour le cas où Q est entre 0 et 1, nous posons P égal à 1 sur Q. En appliquant le résultat précédent à P puissance n, nous obtenons que P puissance n tend vers l'infini. Comme Q puissance n est égal à 1 sur P puissance n, cela tend vers 1 sur l'infini, soit 0.
Enfin, pour le dernier cas, nous utilisons le théorème des gendarmes. Nous posons s égal à moins Q, pour se rapporter au cas précédent. En utilisant le fait que s puissance n tend vers 0, nous pouvons encadrer Q puissance n entre moins s puissance n et s puissance n. Comme les deux encadrements convergent vers 0, nous pouvons conclure que Q puissance n tend également vers 0.
En résumé, nous avons démontré les trois cas de la limite des suites géométriques. Le premier cas nécessite l'utilisation de l'inégalité de Bernoulli et constitue une démonstration plus approfondie. Les deux autres cas utilisent des astuces pour simplifier la démonstration. Il est important de connaître cette démonstration par cœur.
Maths SM&SP
Analyse
2BAC SM Maroc

Limite avec A ou Ɛ
La vidéo traite de la définition formelle d'une limite mathématique en utilisant des exemples. L'objectif est de montrer comment ne pas avoir peur de cette définition et de la rendre compréhensible pour les étudiants qui continueront les mathématiques l'année suivante.
L'exemple donné consiste à montrer que pour une suite donnée, Un=3n+2, il est possible de déterminer à partir de quel rang tous les termes de la suite sont supérieurs à un réel donné A.
En traduisant la définition mathématique en français, on comprend que peu importe la hauteur du réel A, on veut montrer qu'à partir d'un certain rang n0, tous les termes de la suite dépassent cette hauteur.
Pour résoudre l'équation 3n+2>A, on trouve que n>A-2/3. Puisque n doit être un entier naturel, on utilise la partie entière de A-2/3 plus 1, pour déterminer le plus petit entier n0 à partir duquel la propriété est vraie.
La vidéo illustre également graphiquement cette idée, montrant que peu importe la hauteur de la barrière fixée (représentée par les réels A1, A2, A3), il existe toujours un rang à partir duquel tous les termes de la suite sont au-dessus de cette barrière.
La définition formelle de la limite est ainsi présentée, soulignant que bien qu'elle puisse paraître complexe au début, elle devient plus simple à comprendre avec la pratique. La FAQ de la vidéo est également mentionnée pour toute question supplémentaire.
Maths SM&SP
Analyse
2BAC SM Maroc

Forme indéterminée 1 : factoriser par terme de plus haut degré
Les méthodes abordées dans ce cours portent sur les différentes formes indéterminées pour le calcul de limites et comment les résoudre. Un exemple courant est celui d'un polynôme en n. Dans ce cas, la règle est que seul le terme de plus haut degré est important et il prédomine. Pour démontrer cela de manière rigoureuse, on factorise le polynôme par le terme de plus haut degré. Ainsi, on obtient la règle suivante : factoriser par le terme de plus haut degré et observer ce qui se passe. Dans l'exemple donné, avec le polynôme n²-n, on factorise par n² et on obtient 1 + 1/n. Comme 1/n tend vers 0 lorsque n tend vers l'infini, il n'y a plus de formes indéterminées. On a alors quelque chose du type "plus l'infini fois 1", ce qui donne une limite qui tend vers plus l'infini. Cette méthode fonctionne pour tous les polynômes, où le coefficient devant le terme de plus haut degré est ce qui compte. Si ce coefficient est positif, la limite sera plus l'infini. C'est ainsi que l'on peut calculer les limites en plus l'infini pour les polynômes.
Maths SM&SP
Analyse
2BAC SM Maroc

Forme indéterminée 2 : la quantité conjuguée
Dans ce cours, nous étudions les méthodes pour les fonctions rationnelles, qui sont des polynômes divisés par d'autres polynômes. La technique utilisée est similaire à celle utilisée pour les polynômes eux-mêmes, c'est-à-dire que l'on factorise le terme de plus haut degré. Par exemple, dans l'exemple donné, nous étudions la suite Vn = 4n² / (n+1), qui est une fonction rationnelle. Nous identifions le terme de plus haut degré, qui est de degré 2, et nous factorisons par n². En bas, le degré est de 1, donc nous factorisons par n. Les n se simplifient ensuite partiellement, et nous obtenons 4n au numérateur divisé par 1 + 1/n qui tend vers 1. Ainsi, nous éliminons l'indétermination et nous voyons que la limite tend vers l'infini. En conclusion, Vn tend vers l'infini.
Ensuite, nous étudions les différents cas de figure pour les fonctions rationnelles. Il y a trois cas possibles : soit le degré de P (le numérateur) est strictement supérieur au degré de Q (le dénominateur) ; dans ce cas, P l'emporte et la limite tend vers l'infini. Soit le degré de Q est strictement supérieur au degré de P ; dans ce cas, Q l'emporte et la limite tend vers 0. Le troisième cas est lorsque le degré de Q est égal au degré de P ; dans ce cas, les deux sont de même ordre de grandeur et la limite tend vers le rapport des coefficients dominants de Q et P. Par exemple, si nous prenons la suite Un = (3n² + 2n + 1) / (4n² + n + 4), nous factorisons par le terme de plus haut degré, n², et nous simplifions pour obtenir 3 + 2n + 1 / n² au numérateur, et 4 + 1/n + 4/n² en bas. Cette limite tend finalement vers 3/4, le rapport des coefficients dominants.
En résumé, pour les fonctions rationnelles, nous avons toujours l'un des trois cas de figure mentionnés ci-dessus. Il est donc important de les prendre en compte lors de l'étude de ces fonctions.
Maths SM&SP
Analyse
2BAC SM Maroc

Limite d'une somme géométrique
En résumé, ce cours explique que lorsqu'on a une somme à calculer, il est important de regarder les termes de la somme pour déterminer s'il s'agit d'une suite arithmétique, d'une suite géométrique ou autre. Dans ce cas précis, il s'agit de termes consécutifs d'une suite géométrique. En utilisant la formule appropriée, on peut calculer la somme en identifiant les valeurs des termes (u0=1, q=3) et en faisant attention au nombre de termes. La formule utilisée en l'occurrence est u0*(1-q^(nombre de termes))/(1-q). En simplifiant les calculs, on constate que la somme tend vers l'infini.
Maths SM&SP
Analyse
2BAC SM Maroc

Trouver à la calculette "le plus petit entier tel que..."
Dans ce cours, nous étudions une suite et tentons de trouver le plus petit entier tel que la valeur de la suite soit supérieure à une certaine valeur. La suite est définie par la relation de récurrence un+1 = 3un, où u0 = 2.
Nous pouvons voir que chaque terme de la suite est obtenu en multipliant le terme précédent par 3. Il est donc clair que les termes de la suite augmentent rapidement et tendent vers l'infini.
En utilisant une calculatrice ou en effectuant de simples calculs, nous pouvons déduire que le sixième terme de la suite, u6, est supérieur à 1000. Par conséquent, le plus petit entier naturel tel que la valeur de la suite soit supérieure à 1000 est 6.
En utilisant un programme simple, nous implémentons une boucle while qui continue tant que la valeur de u est inférieure à 1000. À chaque itération, la valeur de u est mise à jour en la multipliant par 3. Nous incrémentons également un compteur n à chaque itération pour suivre le nombre d'opérations effectuées. À la fin de la boucle, nous imprimons la valeur de n, qui correspond au rang de la suite où la valeur dépasse 1000.
En résumé, il est important de comprendre la logique et l'objectif du programme. Dans ce cas, l'objectif était de déterminer le plus petit entier naturel tel que la valeur de la suite soit supérieure à 1000. Cela peut également être fait sans programme en itérant manuellement, mais l'approche programmée est plus rapide. N'hésitez pas à consulter la FAQ si vous avez des questions.
Maths SM&SP
Analyse
2BAC SM Maroc
Test video
Aucun résumé n'est disponible pour cette vidéo
Maths SM&SP
Analyse
2BAC SM Maroc
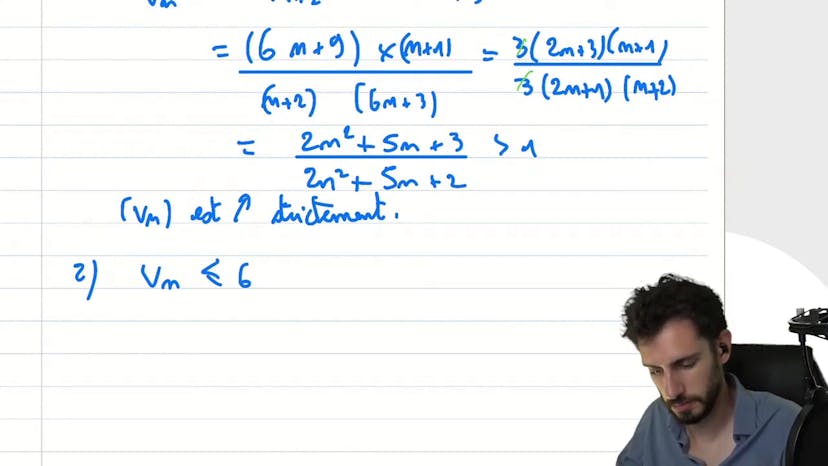
Fraction à transformer
Dans ce cours, on étudie une suite mathématique de la forme vn = 6n + 3 / (n + 1). Pour commencer, nous analysons ses variations en utilisant le critère de croissance qui compare vn+1 / vn avec 1. Nous montrons que ce ratio est supérieur à 1, ce qui signifie que la suite est strictement croissante.
Ensuite, nous déterminons une borne supérieure pour la suite. En particulier, nous prouvons que vn est inférieur ou égal à 6 pour tout n. Ceci est établi en utilisant une équivalence logique qui simplifie l'expression de vn en ajoutant et en soustrayant 6.
Enfin, nous appliquons le théorème de convergence monotone pour conclure que la suite vn converge. En effet, nous avons montré qu'elle est à la fois croissante et bornée, ce qui implique sa convergence. La limite de la suite vn est donc égale à 6.
Maths SM&SP
Analyse
2BAC SM Maroc

Test
car cela ne fonctionne plus dans les dernières versions de l'application. Cependant, il est toujours possible de filmer l'écran et de capturer des images en attendant de résoudre ce problème. Je vais donc essayer d'expliquer les points importants de ce cours de manière SEO friendly.
Dans cette vidéo, l'auteur fait un petit test pour évaluer les fonctionnalités de l'application. Il mentionne qu'il faut jeter une vidéo, ce qui signifie qu'il faut enregistrer une nouvelle vidéo. Il précise également que la durée de cette vidéo sera de quelques minutes.
Ensuite, l'auteur évoque la possibilité de filmer l'écran, mais il n'est pas sûr de ce qu'il faut filmer exactement. Il parle également d'autres sujets plus anciens, sans donner plus de détails à ce propos.
Il continue en disant qu'il y a du son et de l'image dans la vidéo, ce qui est intéressant. Après environ une minute, il annonce qu'il va maintenant passer à la révision, et il montre quelques flèches sur l'écran. Il mentionne également qu'il était endormi dans sa chambre.
Au final, la durée de la vidéo est d'environ une minute et demie. L'auteur mentionne qu'il ne peut plus faire certaines choses, sans spécifier lesquelles.
C'est tout ce que je peux résumer de ce cours en utilisant des termes SEO friendly.
Maths SM&SP
Analyse
2BAC SM Maroc
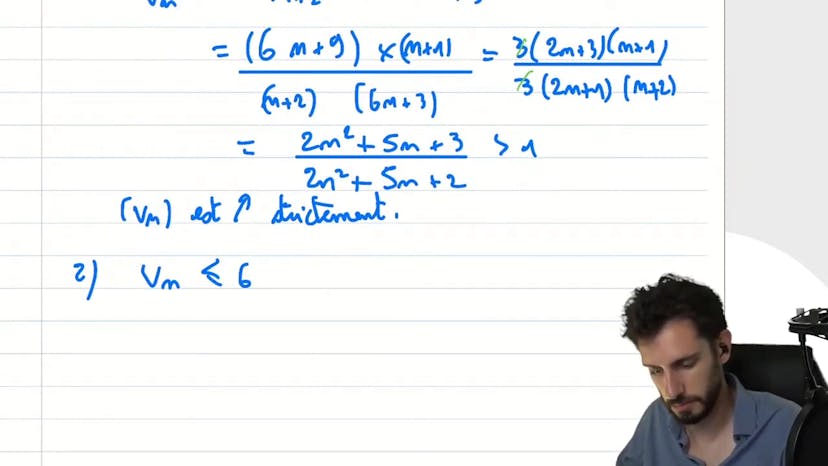
Suite-fraction
La suite vn est une suite définie par vn = 6n + 3 / n + 1. Pour étudier les variations de cette suite, on utilise le critère de croissance en calculant le ratio vn+1 / vn. On simplifie cette expression pour obtenir (2n² + 5n + 3) / (2n² + 5n + 2), qui est strictement supérieur à 1. Ainsi, on peut en déduire que la suite vn est croissante.
Ensuite, on souhaite montrer que cette suite est majorée. On fait la supposition vn + 1 = 6 et on démontre par équivalence que cela est vrai si et seulement si 3 + 1 = 6, ce qui est effectivement vérifié. Donc, on peut affirmer que vn est majorée par 6.
Enfin, on applique le théorème de convergence monotone qui stipule qu'une suite croissante et majorée converge. Ainsi, la suite vn converge vers une limite qui est 6.
Une autre méthode pour étudier les variations de la suite vn consiste à simplifier son expression en écrivant vn = 6n + 3 / n + 1. En effectuant des calculs, on fait apparaitre l'expression 6n + 6 en haut et on compense cela en écrivant innocemment 6(n + 1) - 3. En séparant la fraction, on obtient f(n) = 6 - 3 / (n + 1), qui est une fonction croissante. Ainsi, on peut conclure que la suite vn est également croissante.
De plus, en observant l'expression simplifiée de la suite vn, qui est 6 - 3 / (n + 1), on peut remarquer que lorsque n tend vers l'infini, le terme 3 / (n + 1) tend vers 0. Par conséquent, vn tend vers 6.
En résumé, la suite vn = 6n + 3 / (n + 1) est croissante et majorée par 6, ce qui implique qu'elle converge vers la limite 6.
Maths SM&SP
Analyse
2BAC SM Maroc

Plein de limites !
Pour ce deuxième exercice, nous allons aborder différentes méthodes de gestion des limites. Les deux principales méthodes que nous utiliserons sont la méthode du terme dominant et la méthode de l'encadrement.
Dans la méthode du terme dominant, nous comparons les termes dominants en haut et en bas de la fraction. Par exemple, si nous avons une fraction avec 3n-8 au numérateur et 5n²-1 au dénominateur, nous pouvons dire que 3n-8 est négligeable par rapport à n² et que 5n²-1 est négligeable par rapport à n³ lorsque n devient très grand. Ainsi, nous pouvons simplifier la fraction en n²/n³, qui tend vers 1/2n et donc vers 0.
La méthode de l'encadrement est utilisée lorsque nous avons des puissances négatives et des fonctions trigonométriques comme le cosinus et le sinus. Dans ce cas, nous encadrons ces termes entre -1 et 1. Par exemple, si nous avons une suite avec (-1)^n et le cosinus de n, nous pouvons dire que (-1)^n est compris entre -1 et 1, tout comme le cosinus de n. En utilisant un théorème d'encadrement, nous pouvons conclure que la suite tend vers plus l'infini.
Il est également important de noter que lorsque nous avons des limites finies encadrées des deux côtés, nous pouvons utiliser le théorème des gendarmes pour conclure sur la convergence de la suite.
En résumé, ces méthodes de gestion des limites, la méthode du terme dominant et la méthode de l'encadrement, simplifient le calcul des limites en nous donnant des indications sur le comportement des suites lorsque n tend vers l'infini. Il est essentiel d'encadrer les termes et d'utiliser les théorèmes de comparaison pour obtenir les résultats souhaités.
Maths SM&SP
Analyse
2BAC SM Maroc

Téléscopage !
En résumé, ce cours aborde le sujet des limites de suites définies comme des sommes de termes d'autres suites. Le premier point consiste à déterminer la limite de la suite Un, qui est 1/n et tend vers 0. Ensuite, il faut montrer que pour toutes les valeurs appartenant à n étoiles, Un est égal à 1/n - 1/(n+1). Pour cela, il est conseillé de partir de cette expression et de simplifier jusqu'à obtenir Un. Ensuite, en utilisant la question précédente, on peut calculer la somme Sn. En utilisant une technique appelée somme télescopique, on peut simplifier les termes de la somme et il reste 1 - 1/(n+1). En concluant que la limite de Sn lorsque n tend vers l'infini est 1.
Maths SM&SP
Analyse
2BAC SM Maroc

Majoration astucieuse
Le cours présente une méthode classique pour étudier les variations d'une suite et démontrer sa convergence. La suite en question est Vn = 6n + 3 / (n + 1). Pour déterminer les variations de la suite, on utilise le critère de croissance en comparant le ratio Vn+1/Vn à 1. On montre que ce ratio est supérieur à 1, ce qui signifie que la suite est strictement croissante. Ensuite, on démontre que la suite est majorée par 6 en montrant que Vn < 6 pour tout n. Enfin, on applique le théorème de convergence monotone pour conclure que la suite converge. On peut également utiliser une deuxième méthode pour étudier la suite en travaillant sur son expression. En utilisant des techniques de simplification, on obtient une expression équivalente de la suite et on montre ainsi qu'elle est croissante et bornée par 6. En utilisant les propriétés des limites, on conclut que la limite de la suite Vn est égale à 6.
Maths SM&SP
Analyse
2BAC SM Maroc
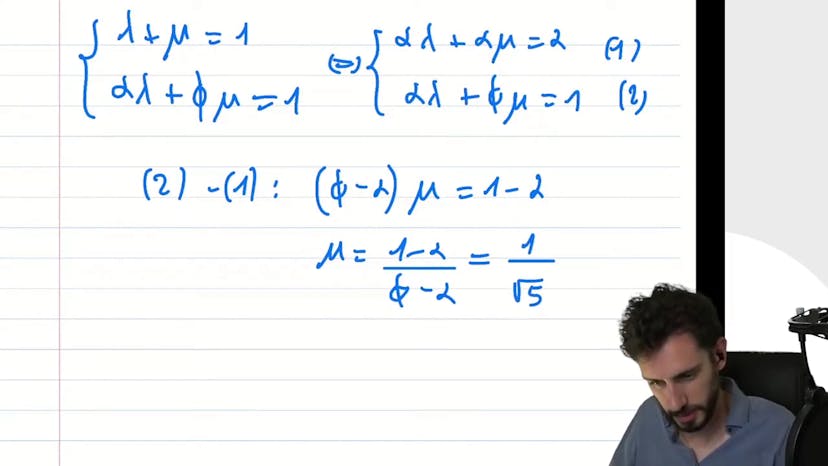
Prépa : Fibonacci
Le cours traite de la suite de Fibonacci et du nombre d'or. La suite de Fibonacci est définie par récurrence où chaque terme est la somme des deux précédents. On nous demande de trouver des réels a, b, lambda et mu tels que chaque terme peut être exprimé comme une combinaison linéaire de sommes géométriques. Plutôt que de traiter immédiatement les 4 inconnues, on cherche d'abord à déterminer s'il existe une seule somme géométrique qui vérifie la relation. On trouve deux possibilités a = (1 - √5)/2 et b = (1 + √5)/2, correspondant au nombre d'or. En utilisant ces valeurs, on résout un système d'équations pour trouver lambda et mu. Une fois que l'on a a, b, lambda et mu, on peut simplifier les calculs en utilisant les propriétés des suites géométriques. On peut ainsi déterminer que b^n tend vers b, qui est égal au nombre d'or. En utilisant cette information, on peut factoriser l'expression et conclure que le terme dominant tend vers 1. Au final, on trouve que la limite de la suite de Fibonacci divisée par le terme précédent tend vers le nombre d'or.


