 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Introduction
Ce cours introduit un nouveau sous-chapitre sur les intégrales et leur lien avec les primitives. Il explique que ce sous-chapitre est assez théorique et demande de la concentration. L'objectif est de trouver des méthodes exactes pour calculer les intégrales, au lieu d'utiliser des approximations. On découvre qu'il existe un lien exact entre le calcul des intégrales et les primitives. Cela permet de calculer les intégrales de manière exacte, ce qui est très intéressant. Ce lien fonctionne dans les deux sens, ce qui permet de calculer les intégrales en utilisant les primitives, mais aussi de trouver des primitives pour des fonctions qui ne sont pas calculables avec des fonctions usuelles. On mentionne également quelques propriétés générales des intégrales, qui sont utiles pour les physiciens et les mathématiciens. Le cours se termine en présentant les points clés du chapitre, notamment le théorème fondamental, la condition suffisante d'existence d'une primitive et des méthodes de calcul des intégrales. L'enseignant encourage les étudiants à poser des questions dans la FAQ et annonce la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Théorème fondamental : énoncé
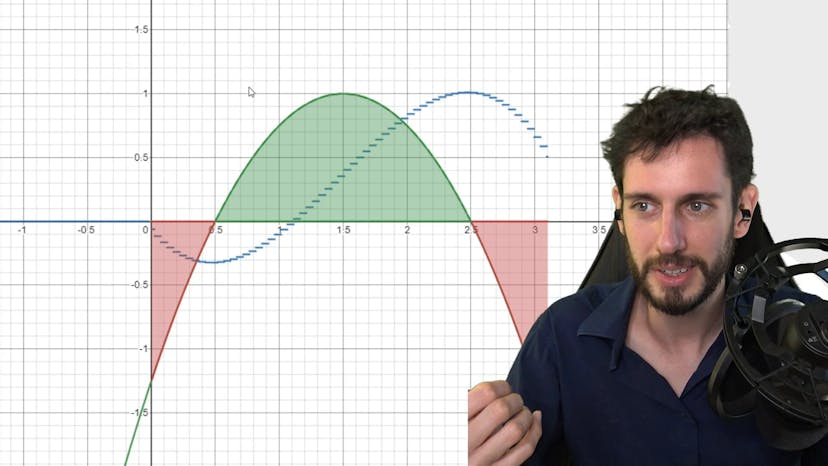
Le théorème fondamental de l'analyse établit un lien entre la notion de primitive et l'intégrale d'une fonction continue et positive sur un intervalle donné. Selon ce théorème, si f est une telle fonction, alors la fonction F définie comme l'intégrale de f entre les points a et x est dérivable, et sa dérivée est égale à f elle-même. Ainsi, F est une primitive de f.
Ce lien peut être visualisé à l'aide d'un graphique représentant une fonction parabole (x²) avec un signe négatif. En calculant l'aire sous la courbe, on constate que celle-ci varie en fonction des valeurs positives et négatives de la fonction.
Plus précisément, l'aire augmente lorsque la fonction est négative et diminue lorsqu'elle est positive. Si la fonction est croissante, l'aire augmente rapidement, tandis que si elle est décroissante, l'aire diminue lentement. Lorsque la fonction atteint zéro, l'aire totale est également de zéro.
Grâce à cette visualisation, il apparaît que la fonction bleue tracée sur le graphique, qui ressemble à une fonction cubique, présente des caractéristiques similaires à celles de la fonction verte (la fonction dérivée). En effet, la fonction bleue décroît lorsque la fonction verte est négative et croît lorsque la fonction verte est positive. Cela suggère que la fonction bleue peut être une primitive de la fonction verte.
Cette visualisation peut être utile pour comprendre le lien entre la primitive d'une fonction et l'aire sous sa courbe. La démonstration formelle de ce lien sera présentée dans une vidéo ultérieure.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Intégrale et Primitive : calcul
Dans cette vidéo, le professeur présente une propriété fondamentale liée au calcul intégral. Il explique que cette propriété diffère du théorème fondamental abordé précédemment.
La propriété démontrée ici est la suivante : si f est une fonction continue et positive sur un intervalle [a, b], et F est une primitive quelconque de f sur cet intervalle, alors l'aire sous la courbe de f entre a et b est égale à la différence entre les valeurs de F en b et en a.
Le professeur précise que cette propriété utilise uniquement les connaissances acquises dans le chapitre des primitives, sans mentionner la forme spécifique de F sous forme d'intégrale.
Il présente également une notation souvent utilisée en mathématiques, où F(b) - F(a) est noté [F(x)]b-a.
Ensuite, le professeur explique que cette propriété peut être généralisée pour des fonctions de tout signe, en considérant toujours une primitive quelconque F. La démonstration de cette généralisation est présentée dans la vidéo.
Le professeur insiste sur le fait que la démonstration repose sur la connaissance de la primitive G obtenue grâce au théorème fondamental. Il explique qu'il existe un K réel tel que toute primitive F de f s'écrive F(x) = G(x) + K.
En utilisant cette expression, le professeur démontre que pour une primitive quelconque F, l'aire sous la courbe de f entre a et b est égale à G(b) - G(a), qui est équivalent à l'intégrale de f entre a et b. Ainsi, la propriété est validée.
En conclusion, le professeur souligne l'importance de connaître les primitives et leur forme pour démontrer cette propriété rapidement. Il invite les élèves à poser des questions s'ils en ont, et annonce la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Propriétés 1 : intuitives !
Dans cette vidéo, nous abordons les propriétés basiques et intuitives de l'intégrale.
La première propriété concerne la linéarité. Si nous prenons l'aire sous la courbe d'une fonction f, nous pouvons la multiplier par un coefficient lambda pour obtenir l'aire sous la courbe de la fonction lambda*f. Par exemple, si nous prenons l'aire sous la courbe x, puis l'aire sous la courbe 2x, nous aurons deux fois plus d'aire.
La deuxième propriété concerne la somme de deux fonctions. Si nous cumulons les aires des fonctions f et g, nous obtiendrons l'aire totale de la fonction f+g. Cela signifie que l'aire totale est égale à l'aire de f plus l'aire de g.
En ce qui concerne les bornes, si f est une fonction continue sur un intervalle [a,b], alors l'intégrale de f entre a et a est égale à zéro. Cela est dû au fait que nous prenons l'aire sous la courbe d'un point a à lui-même, ce qui représente un fil sans dimension.
Par convention, si nous prenons l'intégrale de f entre b et a, cela sera équivalent à l'inverse de l'intégrale de f entre a et b. Donc, si nous parcourons la fonction de b à a, nous plaçons un signe négatif devant l'intégrale.
Enfin, la relation de Schall indique que si nous additionnons l'intégrale de f entre a et c et l'intégrale de f entre c et b, nous obtiendrons l'intégrale de f entre a et b directement. Cela signifie que l'aire totale est égale à l'aire sous la courbe entre a et b, peu importe le point c choisi.
Ces propriétés intuitives de l'intégrale sont importantes à comprendre. J'espère qu'elles sont claires pour vous et je vous retrouve bientôt pour d'autres vidéos sur les propriétés de l'intégrale. À tout de suite !
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Propriétés 2 : remarques pratiques
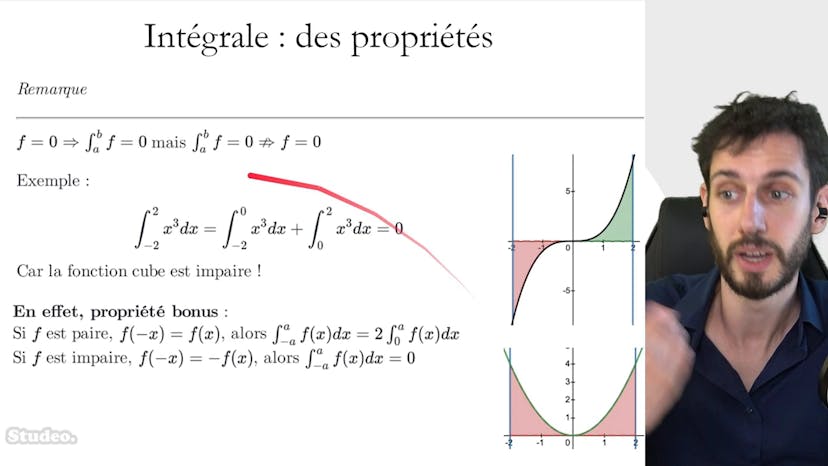
Résumé : Ce cours aborde plusieurs propriétés liées aux fonctions. La première propriété explique que si une fonction est nulle, alors son intégrale sur un intervalle donné sera également nulle. Cependant, il faut faire attention car une fonction dont l'intégrale est nulle ne sera pas forcément la fonction nulle. Une fonction peut avoir une intégrale nulle sur un intervalle donné, tout en ayant une valeur différente de zéro ailleurs.
Ensuite, une deuxième propriété est présentée : si une fonction est paire, c'est-à-dire que pour tout x, f(-x) = f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera égale à deux fois l'intégrale de 0 à A. En revanche, si une fonction est impaire, c'est-à-dire que pour tout x, f(-x) = -f(x), alors l'intégrale sur un intervalle symétrique centré sur 0 sera égale à 0.
Enfin, la dernière propriété aborde les fonctions périodiques. Si une fonction est périodique avec une période T, alors l'intégrale sur un intervalle de taille T sera la même que celle sur un intervalle décalé de T. Cela signifie que l'intégrale entre A et A+T sera toujours égale à l'intégrale entre 0 et T.
Ces propriétés sont très pratiques pour gagner du temps dans l'étude des fonctions et peuvent éviter des erreurs lors de résolution de problèmes.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
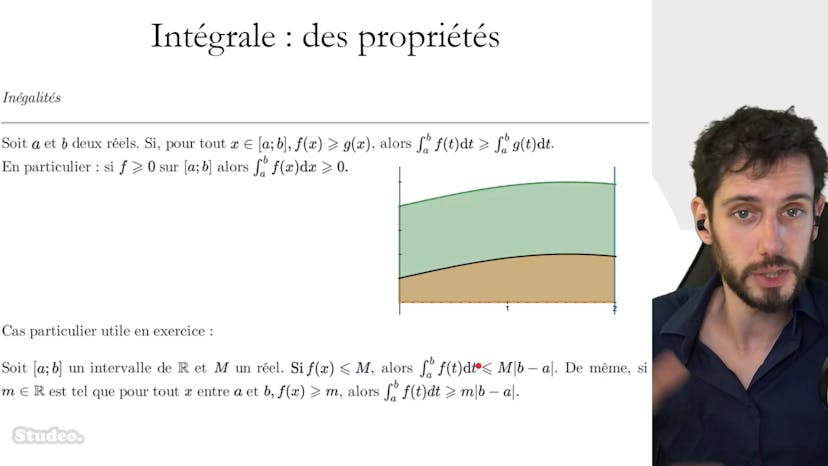
Propriétés 3 : inégalités
Dans cette courte vidéo, nous abordons les propriétés de l'intégrale liées aux inégalités.
Si pour tout x appartenant à l'intervalle entre a et b, la fonction f(x) est toujours supérieure à la fonction g(x), alors les intégrales correspondantes seront également ordonnées de la même manière. En d'autres termes, l'intégrale de f sera plus grande que celle de g.
Ce résultat peut être visualisé avec un dessin. Si f et g sont représentées graphiquement, l'aire sous la courbe de f sera beaucoup plus grande que celle de g.
En particulier, si nous considérons le cas où g est la fonction nulle (c'est-à-dire que g(x) = 0 pour tout x), alors l'intégrale de f sera toujours positive. Cela peut sembler intuitif, mais il est important de connaître cette propriété.
Une autre situation intéressante est lorsque f est inférieure à une fonction constante M. Dans ce cas, M est un majorant de f, ce qui signifie que f est bornée supérieurement. Dans ce contexte, l'intégrale de f entre a et b sera plus petite que l'intégrale de M entre a et b. L'intégrale de M est simplement l'aire d'un rectangle avec une base de longueur b-a (valeur absolue) et une hauteur M.
De manière similaire, si f est supérieure à une constante M (c'est-à-dire que f(x) > M pour tout x), alors l'intégrale de f sera plus grande que l'aire du rectangle en dessous, c'est-à-dire M multiplié par la longueur de l'intervalle (b-a en valeur absolue).
Ces propriétés sont simples mais importantes à connaître. N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires. Je vous retrouverai dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Théorème fondamental : Démo
Dans cette vidéo, nous démontrons le théorème fondamental de l'analyse, qui nous permet de comprendre intuitivement le théorème fondamental. Le théorème affirme que si f est une fonction continue et positive sur un intervalle [a, b], alors la fonction F définie comme l'intégrale de f entre a et x est dérivable et a pour dérivée f.
Nous commençons par rappeler la définition de F(x) comme étant l'intégrale de f entre a et x. Nous remarquons également que F(a) est l'intégrale de f entre a et a, ce qui est nul car c'est l'intégrale d'une fonction sur une largeur nulle.
En utilisant cette définition, nous démontrons que toute fonction continue sur un intervalle [a, b] possède des primitives sur cet intervalle. Cela découle du fait que toute fonction continue a au moins une primitive.
Ensuite, nous entamons la démonstration directe du théorème fondamental. Pour montrer que F est dérivable en x, nous devons étudier la limite du taux d'accroissement. Nous souhaitons que cette limite soit égale à f(x).
Nous prenons un x quelconque dans l'intervalle [a, b] et définissons le taux d'accroissement comme la limite lorsque h tend vers 0 de [F(x+h) - F(x)] / h.
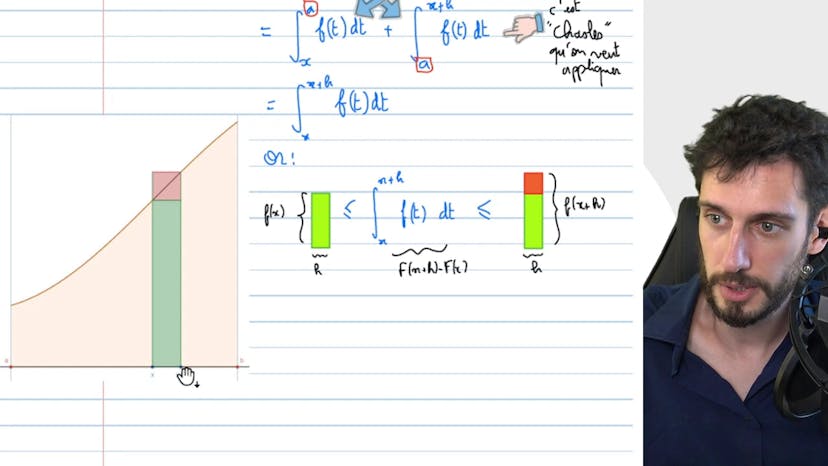
Nous simplifions cette expression en utilisant des propriétés des intégrales. Nous remarquons que l'intégrale entre x et a de f est égale à l'intégrale entre a et x lorsque nous échangeons les bornes d'intégration.
Ensuite, nous utilisons la propriété de Schall pour dire que l'erreur entre x et x+h peut être remplacée par l'erreur entre x et a+h. Nous nous intéressons alors à cette erreur, que nous pouvons encadrer entre l'aire d'un rectangle vert et l'aire d'un rectangle bicolore composé du rectangle vert et d'une portion rouge.
En calculant les aires de ces rectangles, nous obtenons une expression de F(x+h) - F(x) que nous pouvons diviser par h.
Nous remarquons alors que cette expression est encadrée par f(x) et f(x+h). Comme f est une fonction continue, nous pouvons affirmer que la limite de f(x+h) lorsque h tend vers 0 est égale à f(x).
Ainsi, nous avons démontré que le taux d'accroissement de F en x a pour limite f(x), ce qui prouve que F est dérivable et a pour dérivée f.
En conclusion, cette démonstration du théorème fondamental de l'analyse nous montre que toute fonction continue et positive sur un intervalle possède des primitives sur cet intervalle. Cette démonstration utilise des propriétés des intégrales, l'approximation par des rectangles et le théorème d'encadrement pour arriver à cette conclusion.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Calcul d'Intégrale avec Primitive
Ce cours porte sur la méthode du calcul intégral et explique comment calculer une intégrale en utilisant une primitive. Trouver une primitive peut être difficile, mais c'est l'enjeu principal de ce chapitre. Dans l'exemple donné, l'intégrale à calculer est celle de x² moins cos2x de 0 à pi. Pour résoudre cette intégrale, il faut d'abord trouver la primitive de chaque terme de la somme. La primitive de x² est x³ et la primitive de cos2x est ½ sin2x. En appliquant le théorème fondamental, on obtient que l'intégrale de 0 à pi de f2x dx est égale à f2x en pi moins f0, ce qui donne pi³/3. Il est important de faire attention aux signes lors de l'application du théorème fondamental, il est recommandé d'écrire les moins avec des parenthèses pour éviter les erreurs. En développant les calculs, on peut obtenir plus facilement le résultat final, qui est pi³/3 dans cet exemple.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Fonction définie par une Intégrale
Le cours porte sur l'étude des variations d'une fonction définie par une intégrale. L'approche habituelle consiste à calculer la dérivée pour déterminer le signe de cette dérivée, puis en déduire la monotonie de la fonction. Cependant, la particularité ici est que la dérivée d'une intégrale est facile à calculer.
L'exemple étudié concerne la fonction f définie sur l'intervalle [0, π] et égale à l'intégrale de 0 à x de sin^3(t). L'auteur met en garde contre une erreur souvent commise consistant à considérer que la dérivée est simplement sin^3. En réalité, cela dépend des bornes de l'intégrale. Pour illustrer cela, il donne un exemple de l'intégrale de -x à 0 de h(t) dt, où h est une fonction arbitraire. L'application du théorème fondamental de l'analyse permet de corriger cette erreur et de calculer la dérivée correcte.
Ensuite, l'auteur effectue le calcul de la dérivée de la fonction f en posant g(t) = sin^3(t). En appliquant à nouveau le théorème fondamental, il obtient f(x) = g(x) - g(0) = sin^3(x). Ainsi, la fonction f est simplement égale à sin^3(x).
Il souligne également l'importance de différencier les variables utilisées dans l'intégrale et dans l'expression globale de la fonction. La variable t n'a de sens que dans l'intégrale, elle n'est pas utilisée en dehors. La variable x, en revanche, est utilisée dans l'expression globale de la fonction.
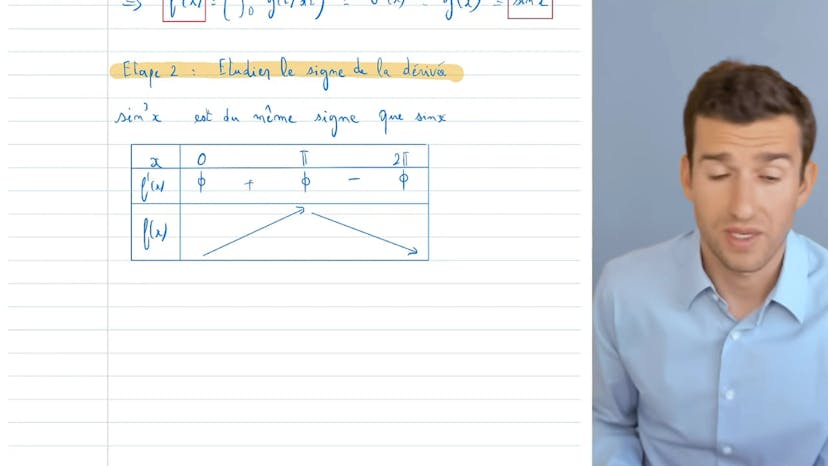
Enfin, l'auteur analyse les variations de la fonction f en étudiant le signe de sa dérivée sin^3(x). Puisqu'il s'agit d'un cube, elle a le même signe que le sinus x sur l'intervalle [0, π]. Il conclut que la fonction f est croissante puis décroissante sur cet intervalle.
En résumé, le cours explique comment étudier les variations d'une fonction définie par une intégrale. Il met en garde contre les erreurs fréquentes et donne des exemples concrets pour illustrer les méthodes de calcul.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Linéarité d'une Intégrale
Dans cette transcription vidéo, on étudie une méthode utilisant la linéarité de l'intégrale pour simplifier le calcul des primitives. On nous demande tout d'abord de montrer que la fonction F proposée est une primitive. Il suffit de dériver la fonction et de vérifier sa dérivabilité sur R, ce qui est assez simple car il s'agit d'un polynôme multiplié par une exponentielle. On obtient donc F de x en dérivant. Donc F est bien une primitive de la fonction donnée.
Ensuite, on nous demande de déterminer l'intégrale de 0 à 1 de 3x moins 2 E de x. Il y a une erreur dans l'énoncé de la question, car "t" est utilisé au lieu de "x". La vraie intégrale que nous voulons calculer est donc 3x moins 2 fois E de x. Dans ce cas, la règle à garder en tête est que lorsqu'un polynôme est multiplié par une exponentielle, on utilise systématiquement une IPP (intégration par parties), car l'objectif est de réduire le degré du polynôme.
Nous posons U de x égal à 3x moins 2, et sa dérivée est 3. Nous posons V égal à E de x, car la dérivée de V est également E de x. Nous avons donc les conditions nécessaires pour appliquer l'IPP. La dérivée de V est facile à primitiver car il s'agit de l'exponentielle.
En utilisant l'IPP, nous obtenons une expression pouvant être calculée rapidement. Ensuite, nous avons l'intégrale de 0 à 1 de 3E2x, ce qui est beaucoup plus simple à calculer. Nous pouvons sortir le 3 et il nous reste seulement à intégrer E2x. La primitive de cette fonction est également E2x, donc nous obtenons E2x entre 0 et 1. En effectuant le calcul, nous obtenons 2E5.
Pour résumer, lorsque nous avons un polynôme multiplié par une exponentielle, nous devons utiliser l'IPP. Dans cet exemple, nous avons utilisé cette méthode pour calculer facilement une intégrale. Si vous avez des questions, n'hésitez pas à les poser dans la faculté.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Encadrer une Intégrale
Dans ce cours, nous apprenons à encadrer des intégrales pour trouver des limites. Nous commençons par étudier une fonction f(x) égale à e^(-x^2). Nous voulons trouver l'encadrement de cette fonction pour tout x supérieur à 1. Nous remarquons que cette fonction est toujours positive car les exponentielles sont toujours positives. Ensuite, pour montrer que f(x) est inférieure à e^(-x), nous multiplions x (qui est supérieur à 1) par -1 pour changer le signe. Ainsi, nous obtenons -x^2 < -x. En composant cette inégalité avec l'exponentielle, nous voyons que f(x) est bien inférieure à e^(-x). En utilisant la propriété de monotonie de l'intégrale, nous pouvons donc encadrer l'intégrale de 1 à 2 de f(x) dx entre 0 et e^(-1) - e^(-2). Ainsi, nous avons résumé comment encadrer une intégrale en utilisant la monotonie de l'intégrale.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
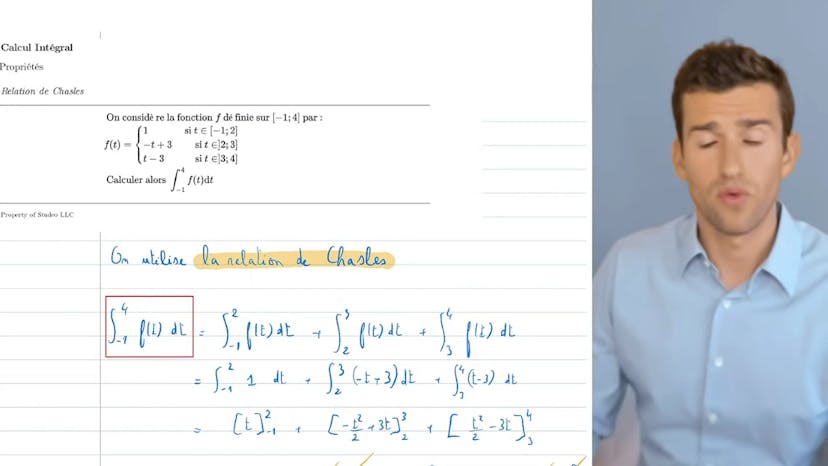
Relation de Chasles
Dans ce cours, nous apprenons comment utiliser la relation de Schall pour calculer une intégrale. La relation de Schall est simple à utiliser. Nous examinons une fonction f qui a différentes expressions selon l'intervalle. Elle est égale à 1 entre -1 et 2, elle est égale à -t+3 entre 2 et 3, et elle est égale à t-3 entre 3 et 4.
Nous sommes ensuite invités à calculer l'intégrale de -1 à 4. Pour cela, nous utilisons la relation de Schall. Nous divisons l'intégrale en trois parties : de -1 à 2, de 2 à 3, et de 3 à 4. Nous utilisons les expressions correspondantes pour chaque partie, qui sont des fonctions courantes et faciles à intégrer.
Nous effectuons les calculs et obtenons 5 comme résultat final. La relation de Schall nous permet de découper l'intégrale en plusieurs morceaux selon nos besoins.
Il est important de faire attention à ce que les chiffres correspondent entre les différentes parties afin d'obtenir un résultat cohérent. Le point de départ doit être -1 et le point d'arrivée doit être 4, mais nous sommes libres de choisir le chemin que nous empruntons pour effectuer les calculs.
En conclusion, la méthode de la relation de Schall est facile à appliquer si nous faisons attention aux détails et respectons les conditions de départ et d'arrivée.
Révisions Maths lycée
Analyse Terminale
BCPST

Introduction
Dans cette vidéo, l'intervenant introduit un nouveau sous-chapitre sur les intégrales et leur lien avec les primitives. Il mentionne que ce sous-chapitre est plus théorique et demande de la concentration.
L'intervenant explique que les méthodes de calcul des intégrales vues précédemment permettent d'obtenir des approximations très précises en ajoutant un grand nombre de rectangles. Cependant, il souligne qu'il est également intéressant de trouver des résultats exacts. Jusqu'à présent, les seules intégrales exactes que l'on peut calculer sont celles des fonctions affines et constantes.
Dans ce sous-chapitre, l'intervenant affirme qu'il existe un lien exact entre le calcul des intégrales et les primitives. Cela permettra de calculer des intégrales de manière exacte, sans approximation. Il précise que ce lien fonctionne dans les deux sens : on pourra utiliser les primitives pour calculer les intégrales de manière exacte, mais aussi approcher des primitives qui ne sont pas calculables.
Ensuite, l'intervenant évoque le besoin, notamment en statistique et probabilité, de calculer des primitives de fonctions telles que l'exponentielle moins x². Il explique qu'il n'existe pas de primitive de cette fonction avec des fonctions usuelles telles que les logarithmes, les sinus ou les exponentielles. On est donc contraints de faire des approximations numériques, notamment par le calcul d'intégrales.
Le reste du chapitre présente quelques propriétés générales sur les intégrales et propose des méthodes de calcul. Parmi les propriétés, on retrouve la relation de Schall, la linéarité, la positivité, la croissance et des inégalités. Les méthodes de calcul incluent l'utilisation de primitives, la linéarité, la relation de Schall, le calcul d'encadrement et l'étude des variations d'une fonction définie par une intégrale.
En conclusion, ce sous-chapitre se concentre sur le lien entre les intégrales et les primitives. Il présente le théorème fondamental, la condition suffisante d'existence d'une primitive, ainsi que des propriétés générales et des méthodes de calcul. L'intervenant encourage les spectateurs à poser des questions dans la FAQ et les salue pour la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

Théorème fondamental : énoncé
Ce cours présente le théorème fondamental de l'analyse, qui lie la notion de primitive et celle d'intégrale (air sous la courbe). Le théorème affirme que si f est une fonction continue et positive sur un intervalle [a, b], alors la fonction F définie par l'intégrale entre a et x de f est dérivable et sa dérivée est égale à f. En utilisant un graphique, le professeur illustre ce théorème en calculant l'air sous la courbe d'une fonction x^2 - x, montrant comment la fonction R (représentant l'air) décroît lorsque la fonction verte (dérivée) est négative et croît lorsque la fonction verte est positive. Cette visualisation permet de comprendre le lien entre l'air sous la courbe et la primitive de la fonction. Le professeur annonce qu'il démontrera formellement ce théorème dans une vidéo ultérieure.
Révisions Maths lycée
Analyse Terminale
BCPST

Intégrale et Primitive : calcul
Dans cette vidéo, nous allons aborder la démonstration d'une propriété importante dans le domaine des intégrales. Cette propriété diffère du théorème fondamental que nous avons vu précédemment. Il est essentiel de comprendre la différence entre ces deux concepts.
La propriété dont il est question ici concerne le calcul d'une intégrale à partir d'une primitive. Nous pouvons utiliser n'importe quelle primitive de la fonction continue et positive sur l'intervalle [a, b]. Il n'est pas nécessaire de spécifier la forme de cette primitive.
L'aire entre a et b sous la courbe de la fonction f est égale à la différence entre la valeur de la primitive en b et la valeur de la primitive en a. En notation mathématique, cela peut s'écrire comme suit : l'intégrale de f entre a et b est égale à F(b) - F(a), où F est une primitive quelconque de f.
Cette définition peut également être généralisée pour des fonctions de tout signe. Dans ce cas, l'intégrale de f entre a et b est toujours égale à F(b) - F(a), peu importe le signe de f.
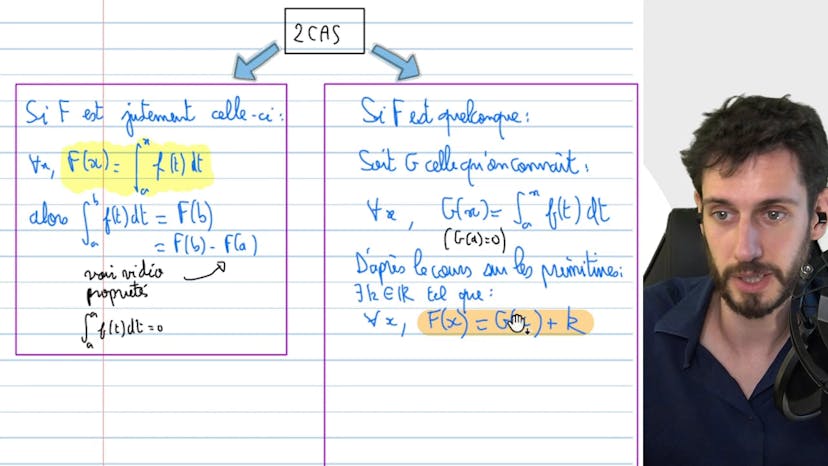
Nous allons maintenant procéder à la démonstration de cette propriété. Nous allons examiner deux cas différents.
Dans le premier cas, supposons que F soit exactement la fonction dont nous parlons dans le théorème fondamental. Dans ce cas, l'intégrale de f entre a et b est égale à F(b) - F(a).
Dans le deuxième cas, où F est une primitive quelconque, nous pouvons l'écrire comme G(x) + K, où G est la fonction du théorème fondamental. Dans ce cas, l'intégrale de f entre a et b reste égale à G(b) - G(a).
En utilisant le fait que G(a) est égal à zéro, nous pouvons réécrire G(b) - G(a) comme G(b). Ainsi, l'intégrale de f entre a et b est égale à G(b), ce qui était la définition du théorème fondamental. Par conséquent, la propriété est démontrée.
Il est important de souligner que pour prouver cette propriété, nous avons utilisé le fait que nous connaissions déjà une primitive de la fonction. Si nous ne l'avions pas, nous aurions utilisé le théorème fondamental pour obtenir une primitive et suivre la même méthode de démonstration.
J'espère que cette démonstration a été claire. N'hésitez pas à poser vos questions dans la FAQ, et rendez-vous dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

Propriétés 1 : intuitives !
Dans cette vidéo, nous couvrons les propriétés assez simples et intuitives de l'intégrale. La première propriété concerne la linearité, qui dit que l'aire sous la courbe d'une fonction est égale à lambda fois l'aire sous la courbe de cette fonction. En d'autres termes, si vous prenez une courbe, l'aire sous la courbe sera doublée si vous prenez une courbe deux fois plus haute.
La deuxième propriété concerne la somme de deux fonctions. Si vous prenez l'aire de la fonction f plus g, cela sera égal à l'aire de f plus l'aire de g. Cette propriété est également intuitive et simple à comprendre.
En ce qui concerne les bornes, si f est une fonction continue sur un intervalle i avec des réels a et b, alors l'intégrale de f entre a et a sera égale à 0. Cela est dû au fait que vous prenez l'aire sous la courbe de la fonction entre un point a et lui-même, qui est essentiellement nulle.
En ce qui concerne la relation de Schall, si vous ajoutez l'intégrale de f entre a et c à l'intégrale de f entre c et b, cela sera égal à l'intégrale de f entre a et b directement. Cette relation permet de découper l'aire totale sous la courbe en deux parties, ce qui est très intuitif.
En résumé, les propriétés de l'intégrale couvertes dans cette vidéo sont simples et intuitives. Elles incluent la linearité, la somme de deux fonctions, les bornes nulles et la relation de Schall.
Révisions Maths lycée
Analyse Terminale
BCPST

Propriétés 2 : remarques pratiques
En résumé, ce cours aborde plusieurs propriétés mathématiques liées aux fonctions. La première propriété concerne la fonction nulle, qui est une fonction plate qui est égale à l'axe des abscisses. Son résultat est nul sur tout intervalle. Cependant, une fonction dont l'intégrale est nulle sur un intervalle ne signifie pas nécessairement que la fonction est nulle. Un contre-exemple est donné pour illustrer ce point.
Ensuite, il est expliqué que si une fonction est paire, c'est-à-dire que pour tout X, f(-X) = f(X), alors l'intégrale de cette fonction sur un intervalle symétrique centré sur 0 sera égale à deux fois l'intégrale de 0 à A. Par contre, si une fonction est impaire, c'est-à-dire que f(-X) = -f(X) pour tout X, alors l'intégrale de cette fonction sur un intervalle symétrique centré sur 0 sera égale à zéro.
Enfin, il est mentionné qu'une fonction périodique de période T aura la propriété que f(X+T) = f(X) pour tout X. De plus, l'intégrale de cette fonction sur n'importe quel intervalle de taille T sera la même.
Ces propriétés peuvent être utiles pour simplifier le calcul ou l'analyse de fonctions, en gagnant du temps grâce à une meilleure compréhension des caractéristiques des fonctions étudiées.
Révisions Maths lycée
Analyse Terminale
BCPST

Propriétés 3 : inégalités
Dans cette courte vidéo sur les propriétés de l'intégrale, il est expliqué que si pour toutes les valeurs de x entre a et b, la fonction f(x) est toujours plus grande que la fonction g(x), alors l'intégrale de f sera plus grande que l'intégrale de g. Cette propriété peut être illustrée graphiquement en montrant que l'aire sous la courbe de f est plus grande que l'aire sous la courbe de g.
De plus, si f(x) est toujours plus petite qu'une fonction constante M, alors l'intégrale de f entre a et b sera plus petite que M multiplié par la longueur de l'intervalle. Si f(x) est toujours plus grande qu'une petite constante M, alors l'intégrale de f sera plus grande que M multiplié par la longueur de l'intervalle.
En résumé, ces propriétés indiquent que si une fonction est majorée, sa valeur intégrale sera aussi majorée par le produit de la constante et de la longueur de l'intervalle. De même, si une fonction est minorée, sa valeur intégrale sera plus grande que le produit de la constante et de la longueur de l'intervalle.
Il est important de connaître ces propriétés pour résoudre certains exercices. Pour plus d'informations, n'hésitez pas à consulter la FAQ ou à attendre la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

Théorème fondamental : Démo
Dans cette vidéo, nous allons démontrer le théorème fondamental de l'analyse, qui a été abordé de manière intuitive dans une précédente vidéo. Le théorème énonce que si f est une fonction continue et positive sur l'intervalle [a, b], alors la fonction F définie comme l'intégrale de f entre a et x est dérivable et sa dérivée est égale à f.
Nous allons commencer la démonstration en fixant un point x appartenant à [a, b], et nous voulons montrer que la fonction est dérivable en ce point. Pour cela, nous devons étudier la limite du taux d'accroissement de la fonction.
En utilisant la définition de la dérivée, nous cherchons à calculer la limite lorsque h tend vers 0 de [f(x + h) - f(x)] / h. Pour cela, nous allons manipuler l'expression de F(x + h) - F(x).
Nous appliquons la définition de F à F(x + h) et à F(x), puis nous utilisons certaines propriétés des intégrales pour réarranger les termes. En utilisant la propriété de Schall, nous pouvons dire que l'intégrale entre x et a suivie de l'intégrale entre a et x + h est équivalente à l'intégrale entre x et x + h.
Nous nous concentrons ensuite sur l'erreur entre x et x + h de la fonction f. Nous utilisons l'approximation de cette erreur par des rectangles, en encadrant l'aire sous la courbe de f entre x et x + h par l'aire d'un rectangle vert et l'aire d'un rectangle bicolore.
En utilisant les propriétés des rectangles, nous obtenons que l'erreur entre x et x + h est inférieure à f(x + h) × h. Divisant les deux côtés par h, nous obtenons l'inégalité f(x) ≤ [F(x + h) - F(x)] / h ≤ f(x + h).
Comme f est continue, nous pouvons dire que la limite de f(x + h) quand h tend vers 0 est égale à f(x). Ainsi, la limite du taux d'accroissement est f(x), ce qui montre que la fonction est dérivable en x avec une dérivée égale à f(x).
En conclusion, nous avons démontré que la fonction F définie par l'intégrale de f entre a et x est dérivable avec une dérivée égale à f. Ce théorème nous permet également de conclure que toute fonction continue sur un intervalle a des primitives sur cet intervalle.
J'espère que cette démonstration a été claire et que vous avez pu suivre les différentes étapes. N'hésitez pas à poser des questions si vous avez des doutes. À bientôt pour une prochaine vidéo !
Révisions Maths lycée
Analyse Terminale
BCPST

Calcul d'Intégrale avec Primitive
Le cours traite de la première méthode de calcul intégral. L'objectif principal de ce chapitre est de trouver une primitive, ce qui peut être assez complexe. La méthode consiste à trouver une primitive, puis à appliquer le théorème fondamental.
Dans cet exercice spécifique, l'intégrale à calculer est celle de x² moins cos2x de 0 à pi. Pour calculer cette intégrale, il suffit de trouver la primitive de x² et la primitive de cos2x, puis de les soustraire. La primitive de x² est x³ et la primitive de cos2x est ½ de sin2x. Cela donne une primitive de la fonction f.
Ensuite, en utilisant le théorème fondamental, l'intégrale de f2x dx de 0 à pi devient f2x en pi moins f0. Après avoir fait les calculs, on remarque que sin(pi) est égal à 0, ce qui simplifie l'expression. Finalement, on obtient pi au cube sur 3 comme résultat de l'intégrale.
This text summarizes the content of a video transcription about the first method of integral calculus. The main goal of this chapter is to find a primitive, which can be quite challenging. The method consists of finding a primitive and then applying the fundamental theorem.
In this specific exercise, the integral to be calculated is x² minus cos2x from 0 to pi. To calculate this integral, one simply needs to find the primitive of x² and the primitive of cos2x, and then subtract them. The primitive of x² is x³ and the primitive of cos2x is ½ sin2x. This gives a primitive of the function f.
Then, using the fundamental theorem, the integral of f2x dx from 0 to pi becomes f2x at pi minus f0. After performing the calculations, it is noticed that sin(pi) equals 0, which simplifies the expression. Finally, the result of the integral is pi cubed over 3.
Révisions Maths lycée
Analyse Terminale
BCPST

Fonction définie par une Intégrale
Ce cours traite des variations d'une fonction définie par une intégrale. Habituellement, pour déterminer les variations d'une fonction, nous calculons sa dérivée pour en déduire le signe et la monotonie. Cependant, la dérivée d'une intégrale est facile à calculer. Par exemple, si nous avons l'intégrale de a à x de u(t), sa dérivée est simplement u(x). Nous pouvons donc étudier le signe de la dérivée pour déterminer les variations, et construire un tableau de variations.
Dans cet exemple, nous devons étudier les variations de la fonction f sur l'intervalle 0 à π, avec f(x) égale à l'intégrale de 0 à x de sin^3(t). Il est important de faire attention, car la dérivée ne dépend pas seulement de la fonction au milieu (ici sin^3(t)), mais aussi des bornes de l'intégrale. Pour illustrer cela, prenons l'exemple de l'intégrale de -x à 0 de h(t)dt, où h est une fonction quelconque. En utilisant le théorème fondamental de l'analyse, nous pouvons réécrire cette intégrale comme l'intégrale de x à 0 de h(t)dt. Ainsi, la dérivée de cette fonction sera -h'(x). Donc, il est crucial de faire attention aux bornes lors du calcul de la dérivée d'une intégrale.
Ensuite, nous calculons la dérivée de la fonction f(x), en utilisant le théorème fondamental de l'analyse. En posant G(x) comme une primitive de g(x) = sin^3(x), nous obtenons f(x) = G(x) - G(0). Lorsque nous dérivons f(x), nous obtenons g(x) (sin^3(x)), ce qui confirme notre fonction initiale. Il est également important de noter que dans cette notation, la variable t utilisée à l'intérieur de l'intégrale est une variable locale, qui n'a de sens qu'à l'intérieur de l'intégrale. La variable x, quant à elle, est une variable globale et a un sens à l'extérieur de l'intégrale.
Enfin, pour étudier les variations de f(x), nous analysons le signe de sa dérivée, qui est sin^3(x). Étant donné que c'est au cube, nous savons que son signe est le même que celui de sin(x) sur l'intervalle 0 à π. Nous constatons que sin(x) est positif sur cet intervalle, puis devient négatif. Par conséquent, f(x) est croissante, puis décroissante. Il est possible de calculer les valeurs spécifiques en 0, π et 2π, mais pour cette question, nous avons simplement étudié les variations.
En résumé, le calcul des variations d'une fonction définie par une intégrale est relativement simple grâce au calcul de sa dérivée. Il est essentiel de faire attention aux bornes de l'intégrale et de comprendre les variables locales et globales utilisées dans le processus.
Révisions Maths lycée
Analyse Terminale
BCPST

Linéarité d'une Intégrale
Dans ce cours, nous étudions une méthode pour calculer les primitives en utilisant la linéarité de l'intégrale. Le professeur nous présente un exercice où il faut montrer que la fonction F proposée est une primitive de la fonction f(x) = x^x.
La première question est une question cadeau, car il suffit de dériver la fonction F pour vérifier si elle est une primitive de f. Comme f(x) est un polynôme multiplié par une exponentielle, la dérivabilité sur R ne pose aucun problème. En dérivant la fonction F, on obtient effectivement f(x), ce qui confirme que F est une primitive de f.
Ensuite, nous devons déterminer l'intégrale de 0 à 1 de la fonction 3t - 2e^(x^x). Cependant, il y a une erreur dans l'énoncé, car le professeur utilise par erreur la variable t au lieu de x. La vraie intégrale que nous voulons calculer est donc l'intégrale de 3x - 2e^(x^x).
Pour résoudre cet exercice, le professeur rappelle une règle générale : lorsque nous avons un polynôme multiplié par une exponentielle, il est souvent utile d'utiliser une intégration par parties (IPP). En utilisant cette méthode, nous posons U(x) = 3x - 2 et V'(x) = e^(x^x). La dérivée de U(x) est simplement 3, et la primitive de V'(x) est également e^(x^x). Nous avons donc les conditions nécessaires pour appliquer l'IPP.
En effectuant les calculs, nous obtenons finalement l'intégrale de 0 à 1 de 3e^(x^x) - 2x. Cette intégrale est plus simple à calculer, car l'exponentielle est facile à primitiver. En résolvant cette intégrale, nous trouvons 2e^5.
En résumé, cette méthode consiste à utiliser la linéarité de l'intégrale pour séparer les termes et simplifier le calcul des primitives. Lorsque nous avons un polynôme multiplié par une exponentielle, l'intégration par parties est souvent une bonne stratégie.
Révisions Maths lycée
Analyse Terminale
BCPST

Encadrer une Intégrale
Le cours porte sur les encadrements d'intégrales pour trouver des limites. On nous propose une fonction f(x) = e^(-x^2) à étudier et on nous demande de l'encadrer pour tout x supérieur à 1. Premièrement, on remarque que la fonction exponentielle est toujours positive, donc f(x) est également positive pour tout x supérieur à 1. Ensuite, pour montrer que f(x) est inférieure à e^(-x), on utilise des manipulations algébriques en observant que x est supérieur à x² et en multipliant par -1 pour inverser le signe. En composant cette inégalité avec l'exponentielle, on obtient l'inégalité souhaitée.
En utilisant la propriété de monotonie de l'intégrale, on en déduit un encadrement de l'intégrale de f(x) de 1 à 2. On sait que pour tout x appartenant à [1,2], 0 est inférieur à f(x) qui est lui-même inférieur à e^(-x). Ainsi, on calcule l'intégrale de 0 de 1 à 2, qui est égale à 0, et l'intégrale de e^(-x) de 1 à 2, qui se résout facilement. On obtient finalement que l'intégrale de f(x) de 1 à 2 est comprise entre 0 et e^(-1) - e^(-2). Cette méthode nous permet donc d'encadrer une intégrale en utilisant la monotonie de celle-ci.
Révisions Maths lycée
Analyse Terminale
BCPST
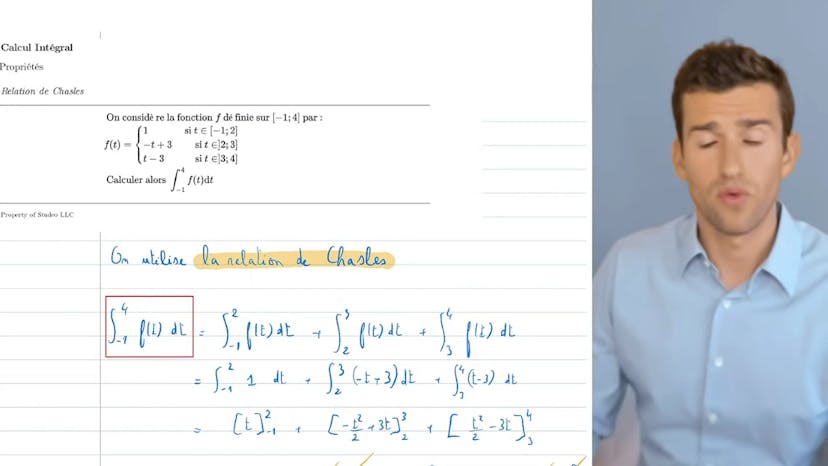
Relation de Chasles
Dans ce cours, nous allons voir la méthode de la relation de Schall en vue d'utiliser le SEO-friendly. La relation de Schall est facile à utiliser. Dans cet exemple spécifique, nous étudierons une fonction f qui a différentes expressions selon l'intervalle. Elle est égale à 1 entre (-1, 2), égale à (-t, 3) entre 2 et 3, et égale à t-3 entre 3 et 4.
La question posée est de calculer l'intégrale de (-1,4). Pour cela, nous utiliserons la relation de Schall. Nous disons que l'intégrale de (-1,4) est égale à l'intégrale de (-1,2), plus 2 à 3, plus 3 à 4. Ceci est assez simple car nous utilisons les expressions dans chaque cas. Ces fonctions sont couramment utilisées et faciles à primitiver. Donc, l'intégrale de 1 est t, l'intégrale de (-t, 3) est (-t², 2, 3t), et l'intégrale de t-3 est l'opposé.
En effectuant les calculs, nous obtenons 3-4-4, ce qui donne un total de 5. Ainsi, nous pouvons facilement jouer avec les vecteurs grâce à la relation de Schall. Nous pouvons découper notre intégrale en plusieurs morceaux selon nos besoins. L'important est de s'assurer que le chiffre ici soit égal à celui-là, de sorte que les résultats se rejoignent correctement. Une fois que nous avons fait attention à cela, il suffit de choisir un point de départ (-1) et un point d'arrivée (4), puis nous pouvons passer par où nous voulons.
En conclusion, en faisant attention à ces détails, la méthode de la relation de Schall s'applique facilement.
Révisions Maths lycée
Analyse Terminale
ECG

Introduction
Dans cette vidéo d'introduction sur les intégrales, nous allons aborder le lien avec les primitives. Ce sous-chapitre est assez théorique et demande une certaine concentration. Les méthodes de calcul de l'intégrale R nous permettent de faire des approximations très précises en ajoutant un nombre de rectangles, mais on cherche souvent des résultats exacts. Actuellement, nous pouvons seulement trouver des résultats exacts pour les fonctions affines et constantes. Cependant, dans ce chapitre, nous verrons qu'il existe un lien exact entre le calcul de l'intégrale R et les primitives. Cela nous permettra de calculer exactement les intégrales, sans aucune approximation. Ce lien fonctionne dans les deux sens : parfois, nous pourrons calculer exactement l'intégrale en utilisant la primitive, ce qui est très intéressant. Mais nous pourrons également aborder des primitives qui ne sont pas calculables. Par exemple, en statistique, nous avons souvent besoin de calculer la primitive de la fonction exponentielle moins x², qui est à la base de la courbe en cloche. Malheureusement, il n'existe pas de primitive utilisant des fonctions usuelles telles que les logarithmes, les sinus ou les exponentielles. Nous devons donc faire une approximation numérique, notamment en utilisant le calcul de l'intégrale R. Dans la suite du chapitre, nous explorerons certaines propriétés des intégrales en général, comme la comparaison entre les fonctions et les intégrales, qui est utile pour les physiciens et les mathématiciens. En résumé, ce sous-chapitre abordera principalement deux points : le lien avec les primitives, avec le théorème fondamental qui définit l'existence d'une primitive et ses conditions suffisantes, ainsi que quelques propriétés générales comme la relation de Chasles, la linéarité, la positivité, la croissance et des inégalités. En ce qui concerne les méthodes, nous utiliserons l'aide d'une primitive pour calculer une intégrale, ainsi que la linéarité, la relation de Chasles et l'encadrement des intégrales. Nous étudierons également les variations d'une fonction définie par une intégrale. N'hésitez pas à poser vos questions dans la FAQ et à me retrouver dans la prochaine vidéo !
Révisions Maths lycée
Analyse Terminale
ECG

Théorème fondamental : énoncé
Dans cette vidéo, le professeur présente le théorème fondamental de l'analyse, qui lie la notion de primitive et l'intégrale d'une fonction continue et positive sur un intervalle. Le professeur utilise un graphique pour illustrer ce lien et rend la notion plus claire. Il explique que lorsque la fonction dérivée est négative, l'air sous la courbe est décroissant, tandis que lorsque la fonction dérivée est positive, l'air sous la courbe est croissant. Cette observation suggère que la fonction présentée dans le graphique, qui ressemble à x^3, pourrait être une primitive. Le professeur annonce qu'il démontrera formellement ce lien dans une vidéo ultérieure. Il encourage les spectateurs à poser des questions ou à demander des précisions en laissant des commentaires.
Révisions Maths lycée
Analyse Terminale
ECG

Intégrale et Primitive : calcul
Dans cette vidéo, nous allons présenter une démonstration d'une propriété fondamentale en mathématiques. Cette propriété est distincte du théorème fondamental que l'on a précédemment étudié. Il est important de faire la distinction entre les deux et de comprendre ce que chacun apporte. La propriété nous dit que l'on peut calculer une intégrale grâce à une primitive. C'est une information très utile. Le théorème fondamental, quant à lui, nous dit que l'on peut trouver une primitive grâce à un calcul intégral. Les deux concepts sont donc différents.
Dans cette démonstration, on nous dit que f est une fonction continue et positive sur un intervalle [a, b]. F est une primitive quelconque de f sur cet intervalle. On ne nous donne pas la forme de F, on ne dit pas si F est exprimée sous forme d'une intégrale ou non. On utilise simplement le concept des primitives. On nous dit que l'aire entre a et b de la fonction f est égale à la valeur de la primitive en b moins la valeur de la primitive en a. Cela n'a donc rien à voir avec le théorème fondamental. Cette propriété est valable pour n'importe quelle primitive de f, peu importe sa forme.
On écrit souvent cette égalité de la manière suivante : F(b) - F(a). C'est une notation compacte pour représenter F(b) moins F(a). Cette notation est utilisée fréquemment en mathématiques pour ce type de concept.
Cette propriété est également valable pour les fonctions qui ne sont pas nécessairement positives sur l'intervalle [a, b]. On peut répéter la même démonstration dans ce cas. On peut donc généraliser cette définition pour toutes les fonctions continues sur [a, b], peu importe leur signe. L'élément important à retenir est que l'on peut démontrer cette propriété de manière générale, pour n'importe quelle fonction.
Maintenant, passons à la démonstration de cette propriété. Nous souhaitons montrer que pour toute primitive F, l'intégrale de f entre a et b est égale à F(b) moins F(a), peu importe la primitive choisie. Nous allons faire deux cas différents pour la démonstration.
Dans le premier cas, supposons que F soit exactement la fonction que nous avons étudiée précédemment dans le théorème fondamental. Dans ce cas, l'intégrale de f entre a et b est effectivement égale à F(b) moins F(a). Cela est tout simplement dû au fait que si nous plaçons b en haut et a en bas dans l'expression, cela nous donne directement F(b) moins F(a). Par ailleurs, nous savons que F(a) est égal à zéro dans ce cas précis, puisque F est la primitive du théorème fondamental. Donc l'équation devient simplement F(b) - 0, ce qui est égal à F(b) moins F(a).
Dans le deuxième cas, supposons que F soit une autre primitive quelconque de f. Nous allons l'appeler G. Nous savons d'après nos connaissances sur les primitives, et en particulier grâce à un théorème important, qu'il n'y a pas d'autres primitives possibles que celle que nous connaissons déjà. Autrement dit, si nous avons trouvé une primitive F, toutes les autres primitives seront simplement des translations de F, avec éventuellement une constante supplémentaire. Ainsi, si F est quelconque, nous pouvons écrire F(x) = G(x) + K, où K est une constante réelle. Cette démonstration repose entièrement sur cette primitive G que nous connaissons.
Au final, nous pouvons donc dire que F(b) moins F(a) est égal à G(b) moins G(a). Et puisque G(a) est égal à zéro, nous obtenons tout simplement G(b) comme résultat final. Or, nous avons déjà démontré que G(b) est égal à l'intégrale de f entre a et b. Donc, quelle que soit la primitive F que nous choisissons, nous trouvons toujours que l'intégrale de f entre a et b est égale à F(b) moins F(a).
Il est important de comprendre la distinction entre les deux théorèmes et de savoir que cette propriété s'appuie sur le fait que nous connaissons l'existence d'une primitive et sa forme, que ce soit la primitive du théorème fondamental ou une autre primitive quelconque. Si vous avez des questions, n'hésitez pas à consulter la FAQ ou à nous les poser. À bientôt pour une prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
ECG

Propriétés 1 : intuitives !
Dans cette vidéo, nous couvrons les propriétés de base de l'intégrale. La première propriété est la linéarité : l'intégrale de la fonction f multipliée par un coefficient lambda est égale à lambda fois l'intégrale de f. La deuxième propriété concerne l'addition des fonctions : l'intégrale de la somme de deux fonctions f et g est égale à l'intégrale de f plus l'intégrale de g. Les bornes de l'intégrale sont également importantes : si f est une fonction continue sur un intervalle [a, b], alors l'intégrale de f de a à a est égale à 0. De plus, l'intégrale de f de b à a est définie comme étant l'opposé de l'intégrale de f de a à b. Enfin, la relation de Chasles stipule que l'intégrale de a à c plus l'intégrale de c à b est égale à l'intégrale de a à b directement. Ces propriétés sont essentielles pour comprendre les calculs d'aires sous des courbes. J'espère que ces explications sont claires et je vous donne rendez-vous pour une prochaine vidéo sur d'autres propriétés de l'intégrale.
Révisions Maths lycée
Analyse Terminale
ECG

Propriétés 2 : remarques pratiques
Le cours est une transcription d'une vidéo donnant des propriétés en mathématiques. La première propriété concerne la fonction nulle et explique que si f est la fonction nulle, alors son intégrale sur un intervalle AB est nulle. Cependant, une fonction dont l'intégrale est nulle sur un intervalle n'est pas toujours nulle. Un contre-exemple est donné pour illustrer cela.
Ensuite, une propriété bonus est présentée : si une fonction est paire (c'est-à-dire que f(-x) = f(x) pour tout x), alors l'intégrale sur un intervalle symétrique centré sur zéro est égale à deux fois l'intégrale de 0 à A. En revanche, si une fonction est impaire (c'est-à-dire que f(-x) = -f(x) pour tout x), alors son intégrale sur un intervalle symétrique centré sur zéro est nulle.
Enfin, une dernière propriété bonus est énoncée pour les fonctions périodiques de période T. Si une fonction est périodique de période T, alors l'intégrale sur n'importe quel intervalle de taille T est égale à l'intégrale entre 0 et T.
Ces propriétés sont utiles pour gagner du temps lors de l'étude de fonctions et permettent de mieux comprendre leur comportement. La vidéo se termine en invitant les spectateurs à rester attentifs pour la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
ECG

Propriétés 3 : inégalités
Dans cette courte vidéo, nous abordons les propriétés de l'intégrale liées aux inégalités. Tout d'abord, si pour toutes les valeurs de x comprises entre a et b, la fonction f(x) est toujours supérieure à la fonction g(x), alors les intégrales correspondantes seront ordonnées de la même manière. Plus précisément, l'intégrale de f sera plus grande que l'intégrale de g. Cette propriété peut être illustrée graphiquement, où l'aire sous la courbe de f sera beaucoup plus grande que celle de g.
Une propriété intéressante est que si g est la fonction nulle (c'est-à-dire toujours égale à zéro), alors l'intégrale de la fonction f sera toujours positive. Cela peut sembler intuitif mais il est important de connaître cette propriété, car elle est utile dans les exercices.
Dans le cas où nous avons deux fonctions ordonnées de la manière suivante : f(x) est inférieure à une fonction constante égale à M, nous pouvons dire que M est une borne supérieure de f, ce qui signifie que f est bornée supérieurement. Dans ce cas, l'intégrale de f entre a et b sera plus petite que l'intégrale de M entre a et b. L'intégrale de M, étant une fonction constante, correspond à l'aire d'un rectangle qui est égale à M multiplié par la longueur de l'intervalle (b moins a en valeur absolue pour éviter les problèmes de signes). Par conséquent, nous pouvons dire que si f est bornée supérieurement, la valeur de son intégrale est également bornée supérieurement, et elle est bornée supérieurement par M multiplié par la longueur de l'intervalle.
De la même manière, si f est bornée inférieurement (c'est-à-dire que pour toutes les valeurs de x, f(x) est supérieure à une valeur M), nous aurons l'intégrale qui sera plus grande que l'aire du rectangle situé en dessous de la courbe, c'est-à-dire M multiplié par la longueur de l'intervalle (b moins a en valeur absolue).
Ces propriétés sont simples, mais il est important de les connaître. N'hésitez pas à poser des questions dans la FAQ si vous avez des doutes, et je vous retrouve dans la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
ECG

Théorème fondamental : Démo
Dans cette vidéo, on démontre le théorème fondamental de l'analyse. On définit la fonction F comme l'intégrale entre a et x de la fonction f. Cette fonction F est dérivable et sa dérivée est f. Une conséquence de ce théorème est que toute fonction continue sur un intervalle a, b a des primitifs sur cet intervalle. Pour démontrer le théorème, on commence par étudier la limite du taux d'accroissement de F en un point x. On utilise la propriété de Schall pour simplifier l'expression et on encadre l'erreur entre x et x+h par l'aire de deux rectangles. On montre ensuite que la limite de cette expression est f(x), ce qui prouve que F est dérivable avec une dérivée f. La démonstration peut être effectuée pour un h positif ou négatif.
Révisions Maths lycée
Analyse Terminale
ECG

Calcul d'Intégrale avec Primitive
Dans ce cours sur le calcul intégral, nous abordons la méthode de calcul d'une intégrale à l'aide d'une primitive. Le principal défi de ce chapitre est de trouver une primitive, ce qui peut être difficile par rapport à la dérivation qui est souvent plus simple. Nous allons donc nous concentrer sur cette étape.
Dans cet exercice spécifique, nous devons calculer l'intégrale de 0 à pi de x² moins cos2x. La première étape est de trouver une primitive de cette fonction. Comme nous avons affaire à une somme, la primitive de la somme est égale à la somme des primitives. Il suffit donc de trouver les primitives de x² et de cos2x.
La primitive de x² est x³ et la primitive de cos2x est ½ sin2x. Nous avons donc bien trouvé une primitive pour notre fonction f.
Une remarque importante est que la primitive de coskx est 1/k sinx, ce qui nous permet de trouver la primitive de cos2x. Nous vérifions ensuite que lorsque nous dérivons cette primitive, nous retombons bien sur la fonction initiale.
Nous appliquons ensuite simplement le théorème fondamental en substituant les bornes de l'intégrale par la fonction primitive. Il est important de faire attention aux signes lors de cette étape, car les erreurs de signes sont courantes.
En développant les calculs, nous remarquons que le sinus de pi est égal à 0, ce qui nous permet d'éviter des erreurs de signes. Finalement, nous obtenons le résultat de l'intégrale, qui est pi³/3.
C'est ainsi que nous avons calculé notre première intégrale en utilisant la méthode des primitives.
Révisions Maths lycée
Analyse Terminale
ECG

Fonction définie par une Intégrale
Dans ce cours, nous allons étudier les variations d'une fonction définie par une intégrale. Habituellement, nous calculons la dérivée pour déterminer le signe de la dérivée et la monotonie de la fonction. Cependant, dans le cas d'une dérivée d'une intégrale, le calcul est plus facile. Pour trouver les variations de la fonction f sur l'intervalle de 0 à π, avec f(x) égal à l'intégrale de 0 à x de sin^3(t), il est important de faire attention aux bornes. Une erreur fréquente est de penser que la dérivée de l'intégrale est simplement le terme du milieu, c'est-à-dire sin^3(t). Cependant, cela dépend des bornes de l'intégrale. Par exemple, si nous calculons l'intégrale de -x à 0 de h(t)*t, avec h une fonction quelconque, nous devons prendre en compte les bornes et appliquer le théorème fondamental du calcul intégral. En faisant cela, nous obtenons h(0) - h(x), qui, lorsqu'il est dérivé, devient -h'(x). Dans le cas spécifique d'une intégrale d'une constante, le résultat dépendra des bornes et peut être soit 0, soit une autre valeur. Il est donc important de réfléchir et de ne pas appliquer le résultat de manière automatique. Dans cet exemple, la dérivée de la fonction f, définie comme l'intégrale de 0 à x de sin^3(t), est sin^3(x), ce qui correspond à g'(x) lorsque g(x) est une primitive de sin^3(t). En étudiant les signes de cette dérivée, on remarque que sin^3(x) est du même signe que sin(x) sur l'intervalle de 0 à π. Ainsi, la fonction f est croissante de 0 à π/2, puis décroissante de π/2 à π. Les valeurs aux extrémités de l'intervalle, c'est-à-dire en 0 et en π, peuvent également être calculées, mais cela n'était pas demandé dans cet exercice. En conclusion, il est relativement simple de calculer les variations d'une fonction définie par une intégrale, à condition de faire attention aux bornes et de ne pas confondre les variables internes et externes. Si vous avez des questions supplémentaires, n'hésitez pas à les poser dans la FAQ.
Révisions Maths lycée
Analyse Terminale
ECG

Linéarité d'une Intégrale
Dans ce cours, nous utilisons la linéarité de l'intégrale pour simplifier le calcul des primitives en séparant les termes.
Dans la première partie du cours, nous étudions une fonction f(x) = x^2. Nous devons montrer que la fonction F(x) proposée est une primitive de f(x). Nous utilisons la dérivation pour cela, en justifiant la dérivabilité sur R. Comme f(x) est un polynôme multiplié par une exponentielle, nous n'avons aucun problème de dérivabilité. En dérivant le produit, nous obtenons à nouveau f(x), ce qui confirme que F(x) est bien une primitive.
Ensuite, nous devons déterminer l'intégrale de 0 à 1 de la fonction 3t - 2e^x. Cependant, il y a une confusion dans l'énoncé, car il utilise le symbole "t" qui n'est pas défini. La véritable intégrale que nous devons calculer est de 3x - 2e^x. Pour trouver une primitive de cette fonction, nous utilisons la règle selon laquelle lorsque nous avons un polynôme multiplié par une exponentielle, nous utilisons systématiquement une intégration par parties pour réduire le degré du polynôme. Nous posons U(x) = 3x - 2 et sa dérivée est 3. La fonction V(x) est la même que U(x) car l'exponentielle est facile à primitiver. Nous avons donc tous les éléments pour faire notre intégration par parties.
En utilisant cette technique, nous obtenons une expression qui est plus facile à calculer. L'intégrale de 0 à 1 de 3e^(2x) devient très simple à intégrer. Nous obtenons finalement le résultat de l'intégrale sous forme numérique, qui est égal à 2e^5.
En résumé, lorsque nous avons un polynôme multiplié par une exponentielle, nous devons penser à utiliser l'intégration par parties. Cette méthode nous permet de simplifier le calcul des primitives.
Révisions Maths lycée
Analyse Terminale
ECG

Encadrer une Intégrale
Dans ce cours, nous apprenons à encadrer des intégrales pour trouver des limites. Nous commençons par étudier la fonction f(x) = e^(-x^2). Nous voulons trouver l'encadrement de cette fonction pour tout x supérieur à 1.
Nous constatons que f(x) est toujours positive pour tout x supérieur à 1, car une exponentielle est toujours positive. Ensuite, nous voulons montrer que f(x) est inférieur à e^(-x). Nous commençons par multiplier x par lui-même, ce qui ne change pas le signe de nos inégalités car x est positif. Ensuite, nous multiplions par -1, ce qui change le signe de x^2 en -x^2. Puis, en composant cette expression avec l'exponentielle, qui est une fonction strictement croissante, le signe de nos inégalités ne change pas. Ainsi, nous obtenons l'inégalité voulue.
En utilisant la monotonie de l'intégrale, nous déduisons ensuite un encadrement de l'intégrale de 1 à 2 de f(x) dx. Pour tout x appartenant à [1, 2], nous avons 0 inférieur ou égal à f(x) inférieur ou égal à e^(-x). Nous intégrons chacune de ces deux fonctions, ce qui nous donne l'intégrale de 1 à 2 de 0, qui est évidemment 0, et l'intégrale de 1 à 2 de e^(-x), que nous savons facilement primitiver (-e^(-x)). Finalement, nous avons encadré notre intégrale entre 0 et e^(-1) - e^(-2). Ainsi, nous avons illustré comment encadrer une intégrale en utilisant la monotonie de l'intégrale.
Révisions Maths lycée
Analyse Terminale
ECG
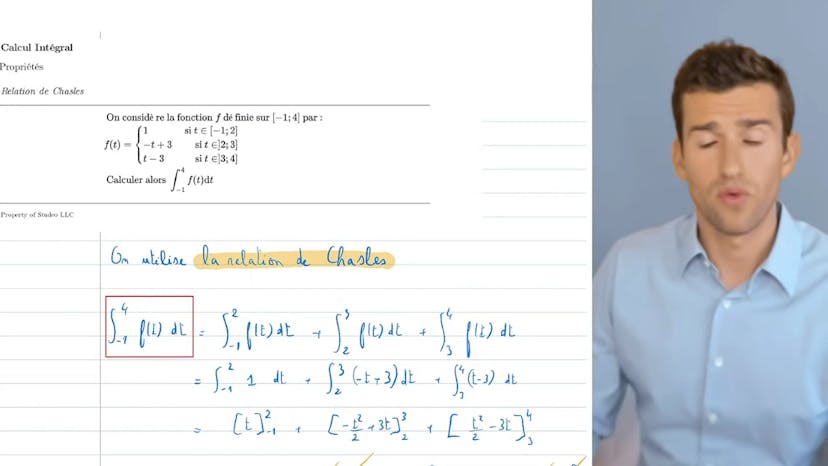
Relation de Chasles
La méthode présentée dans cette vidéo explique comment utiliser la relation de Schall pour calculer une intégrale. La relation de Schall est simple à utiliser et s'applique dans ce cas particulier à une fonction f qui a différentes expressions selon l'intervalle. Elle vaut 1 entre (-1,2), (-t,3) entre 2 et 3, et t-3 entre 3 et 4. Pour calculer l'intégrale de (-1,4), on utilise la relation de Schall en divisant l'intégrale en trois parties : (-1,2), 2 à 3 et 3 à 4. Les expressions des fonctions dans chaque cas sont faciles à primitiver. On obtient les résultats en effectuant les calculs, qui donnent 5 au final. La relation de Schall permet de découper l'intégrale en plusieurs morceaux selon les besoins, tant que les points de départ et d'arrivée correspondent. Cette méthode s'applique facilement si l'on fait attention à ces détails.


