Cours de Convexité en Ligne par les Meilleurs Professeurs - Convexité

Intuition et déf

Le cours explique les notions de convexité et de concavité. Il mentionne qu'une fonction est convexe lorsque sa courbe est en dessous de toute corde qui relie deux points de cette courbe. À l'inverse, une fonction est concave lorsque sa courbe est au-dessus de toute corde reliant deux points. La définition mathématique officielle est également introduite, mais il est souligné qu'il n'est pas nécessaire d'avoir une fonction continue et dérivable pour être convexe ou concave. La vidéo se termine en mentionnant que l'explication complète de la continuité sera abordée dans une prochaine vidéo.

Fonctions usuelles

Dans cette petite vidéo rapide, nous allons parler des fonctions classiques et de leurs caractéristiques. Tout d'abord, nous avons la fonction racine et la fonction log. Ces deux fonctions sont concaves, ce qui signifie que leur graphique a une certaine courbe vers le bas. D'autre part, nous avons également les fonctions x carré et exponentielle x, qui sont convexes. Leur graphique a une forme de sourire, ce qui indique qu'ils sont généralement convexes. Ensuite, nous pouvons dire que la fonction 1 sur x est convexe sur r plus étoile et concave sur r moins étoile. Pour vérifier cela, il faut tracer leurs graphiques respectifs. En bonus, si nous nous concentrons sur r plus (la partie droite du graphique), nous pouvons retenir une règle hors programme. Si nous prenons un alpha positif et que nous considérons les fonctions x puissance alpha avec alpha entre 0 et 1, nous obtenons des fonctions qui ressemblent à la racine carrée et qui sont concaves. D'autre part, les fonctions x puissance alpha avec alpha supérieur à 1 (comme x carré ou x cubique) sont convexes. Si nous explorons r moins, la convexité des fonctions dépendra de la parité de la puissance (x2, x4, x6 seront convexes, tandis que x3, x5, etc seront concaves). En résumé, nous pouvons dire que les racines sont toujours concaves, les puissances supérieures à 1 sont toujours convexes et lorsque la puissance est égale à 1, la fonction est une droite qui peut être à la fois convexe et concave. En traçant quelques exemples de fonctions x puissance alpha avec différents alpha, nous pouvons observer ces caractéristiques. En conclusion, ce cours rapide sur les fonctions classiques peut vous donner une bonne culture générale sur le sujet. N'hésitez pas à poser des questions si nécessaire.

Inégalité fondamentale

Dans cette vidéo, nous allons étudier la relation entre une courbe et ses sécant. Nous avons déjà vu qu'une fonction convexe est située en dessous de ses sécant. Pour illustrer cela, nous pouvons observer le graphe suivant : une courbe rouge située sous des sécant bleues. Pour traduire cette relation, nous allons comparer la différence d'ordonnée entre un point sur le segment bleu et un point sur le segment rouge, pour une même abscisse située entre les abscisses A et B. Nous allons comparer ces deux points : celui sur le segment et celui sur la courbe rouge. L'idée est de démontrer que lorsque nous avons une fonction convexe, le point situé sur le segment a une ordonnée plus élevée que le point de même abscisse situé sur la courbe rouge. Cette inégalité sera un élément important de notre étude. Avec ces informations en tête, nous pouvons introduire un point d'abscisse intermédiaire entre A et B. Nous allons nommer ce point T, situé entre 0 et 1. En pondérant les abscisses de A et de B, nous pouvons calculer une moyenne. Ensuite, nous comparons l'image de ce point intermédiaire par la fonction F (la courbe rouge) avec l'image de cette abscisse par l'équation du segment bleu (la sécant). La difficulté dans cette démonstration est de montrer que cette expression, TF2X + (1-T)F2Y, correspond bien à l'image du point d'abscisse intermédiaire sur le segment. La démonstration complète est un peu complexe, mais si vous êtes intéressé, je peux la présenter dans une autre vidéo. En résumé, nous avons montré que pour une fonction convexe, le point intermédiaire entre deux points sur la sécant a une ordonnée plus élevée que le point correspondant sur la courbe. Cette inégalité est une traduction directe de la différence de position entre la courbe et la sécant. De plus, il existe un lien logique entre convexité et concavité : si une fonction est convexe, sa fonction inverse est concave et vice versa. N'hésitez pas à poser vos questions dans le forum et je vous retrouve dans la prochaine vidéo bonus pour la démonstration complète.

Lien dérivation

Dans ce cours, nous abordons le concept de convexité d'une fonction dérivable. La convexité d'une fonction ne dépend ni de sa continuité ni de sa dérivabilité, mais seulement de la relation entre les sécantes et la courbe de la fonction. Cependant, lorsque la fonction dérivée est existante, nous pouvons avoir des approches et des définitions de la convexité plus pratiques au quotidien. Nous supposons que la fonction f est dérivable sur un intervalle i. Dans ce cas, la fonction f est dite convexe sur i si, pour tout réel x de cet intervalle, la dérivée f' est croissante. De même, la fonction f est dite concave sur i si la dérivée f' est décroissante. Pour illustrer ce concept, prenons l'exemple de la fonction cubique. On peut observer que cette fonction est concave au début, puis devient convexe. En examinant la dérivée de la fonction, on constate que la courbe de la dérivée est décroissante lorsqu'elle est concave et croissante lorsqu'elle est convexe. Nous pouvons également étudier la dérivée seconde de la fonction, qui représente la dérivée de la dérivée. Si la dérivée seconde est positive, la fonction est convexe sur les intervalles correspondants, tandis que si elle est négative, la fonction est concave. Ainsi, pour étudier la convexité d'une fonction dérivable, il est suffisant de calculer la dérivée seconde de sa dérivée et de déterminer les variations de celle-ci. L'étude de la convexité est donc simplifiée grâce à cette méthode. Si vous avez des questions ou des doutes, n'hésitez pas à les poser dans le forum.

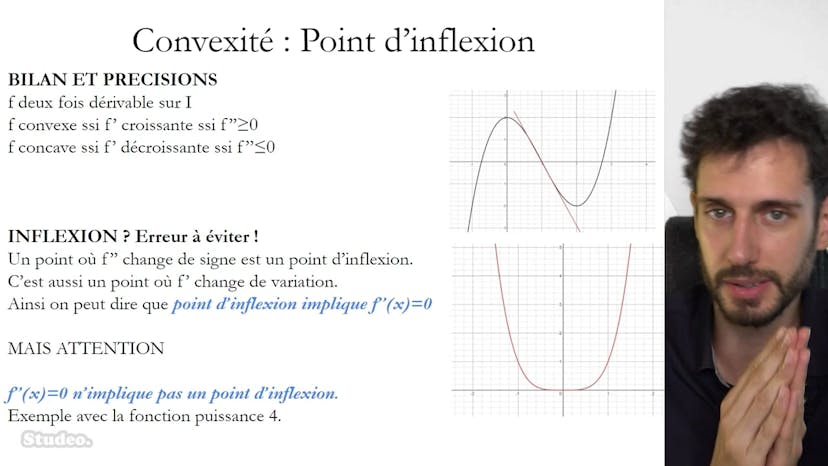
Point d'inflexion

Le cours traite de la notion de point d'inflexion dans les fonctions. Un point d'inflexion est défini comme un point où la courbe de la fonction traverse sa tangente. Visuellement, cela correspond à un changement de comportement de la fonction entre concavité (courbe en haut des sécantes) et convexité (courbe en bas des sécantes), ou vice versa. Un point d'inflexion est également un point de pente maximale de la tangente, où la pente atteint un maximum en valeur absolue. Le cours rappelle également une erreur courante : un point où la dérivée seconde est égale à zéro n'est pas forcément un point d'inflexion, il faut qu'il y ait un changement de comportement de la fonction. Finalement, le cours présente une relation entre la convexité de la fonction et le signe de sa dérivée première : une fonction est convexe si et seulement si sa dérivée première est croissante et positive, et elle est concave si et seulement si sa dérivée première est décroissante et négative.

Démo inégalité convexité

Le cours consiste en la démonstration que le point M, situé entre les points A et B, se trouve également sur la droite AB. Pour cela, le professeur utilise l'équation de la droite AB (Y = AlphaX + Beta) où Alpha est le coefficient directeur et Beta est l'ordonnée à l'origine. Il prouve ensuite que le point M appartient bien à cette droite en remplaçant les coordonnées de M dans cette équation. Si le résultat est égal à l'ordonnée de M, cela signifie que M est sur la droite. En conclusion, puisque le segment AB est au-dessus de la courbe CF (où F est une fonction convexe), l'image de l'ordonnée de M par la droite AB est au-dessus de son image par F.

Démo au programme : convexité et f''

Ce cours aborde les propriétés graphiques et le lien entre la dérivée seconde et la convexité d'une fonction. Si la dérivée seconde d'une fonction f est positive sur un intervalle i, alors la courbe représentative de f est au-dessus de ses tangentes sur cet intervalle. La démonstration consiste à mettre tout du même côté de l'équation de la tangente, poser une fonction qui compare la courbe avec la tangente, et étudier les variations de cette fonction. En montrant que cette fonction est positive ou nulle sur l'intervalle i, on conclut que la courbe est au-dessus de la tangente. La maîtrise de cette démonstration permet de mieux comprendre les concepts et d'être capable de la reproduire sur une feuille blanche.

Convexité et f''

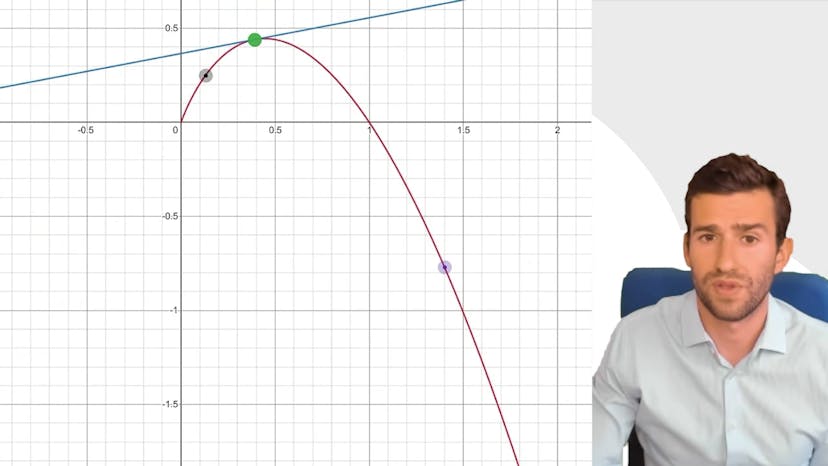
Dans ce cours, nous étudions la convexité d'une fonction, ce qui permet de déterminer certaines propriétés intéressantes, notamment la position de la tangente par rapport à la courbe. Dans le premier exemple, nous examinons la fonction f(x) = (1/3)x³ - (3/2)x² + 2x + 1. Nous dérivons cette fonction deux fois et obtenons la dérivée seconde f''(x) = 2x - 3. En analysant le signe de cette dérivée, nous concluons que f est concave pour x < 3/2 et convexe pour x > 3/2. Pour le deuxième exemple, nous étudions la fonction f(x) = 3x - 3x√x. Comme la fonction n'est pas définie pour x < 0 et n'est pas dérivable en 0, nous étudions sa convexité sur l'ensemble des réels positifs. En dérivant f deux fois, nous obtenons f''(x) = -9/(4√x). Comme cette dérivée est toujours négative, nous concluons que f est concave sur tout son ensemble de définition. La concavité d'une courbe signifie que la tangente est toujours au-dessus de la courbe. Il n'y a qu'un seul point de séquence entre la tangente et la courbe. De plus, la courbe est toujours au-dessus des cordes définies par deux points de la courbe. En utilisant la concavité et la convexité, il est possible de déterminer la position relative d'une tangente par rapport à une courbe. Une fonction concave sera en dessous de sa tangente, tandis qu'une fonction convexe aura sa tangente en dessous de la courbe. Cela résume les principaux concepts abordés dans ce cours sur la convexité des fonctions.

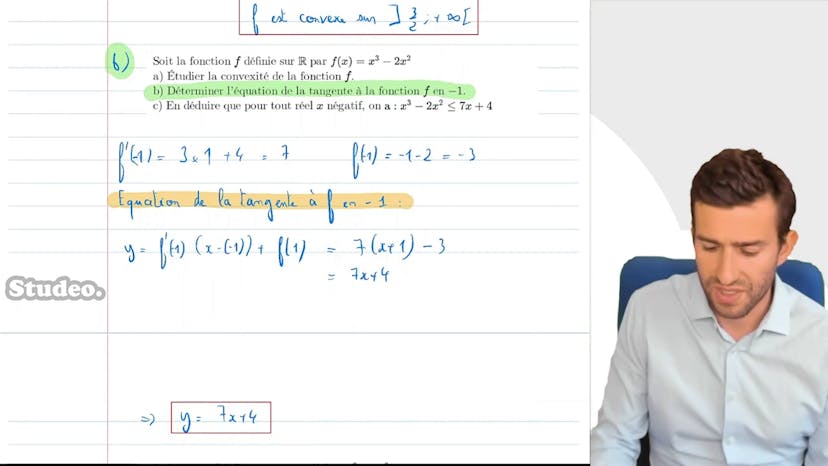
Convexité et Inégalités

Dans ce cours, nous allons étudier la convexité d'une fonction et utiliser cette information pour résoudre des inéquations. Nous commençons par prendre la fonction f(x) = x^3 - 2x^2 et nous calculons ses dérivées f'(x) = 3x^2 - 4x et f''(x) = 6x - 4. Nous étudions le signe de f''(x) pour déterminer la concavité et la convexité de f(x). En résolvant 6x - 4 > 0, nous trouvons que x > 3/2 et en résolvant 6x - 4 < 0, nous trouvons que x < 3/2. Ainsi, nous concluons que f(x) est concave sur l'intervalle (-∞, 3/2) et convexe sur l'intervalle (3/2, +∞). Ensuite, on nous demande de calculer l'équation de la tangente à f(x) en x = -1. En utilisant les formules appropriées, nous obtenons l'équation de la tangente y = 7x + 4. Nous utilisons cette information pour déduire que pour tout x négatif, x^3 - 2x^2 < 7x + 4. Cette inégalité signifie géométriquement que la courbe de f est en dessous de sa tangente, ce qui est le cas lorsque la fonction est concave. Comme nous avons prouvé précédemment que f(x) est concave sur l'intervalle (-∞, 3/2), nous pouvons conclure que l'inégalité est vérifiée dans cet intervalle. Nous illustrons cette propriété en traçant la courbe et la tangente correspondante. Enfin, nous rappelons l'importance de la convexité dans la résolution des inéquations, car sans cette connaissance, l'équation serait plus difficile à résoudre.

Points d'Inflexion

Ce cours est une transcription d'une vidéo qui explique une méthode pour étudier la convexité d'une fonction et trouver ses points d'inflexion. En utilisant la fonction f2x comme exemple, l'orateur explique comment dériver cette fonction deux fois pour déterminer ses variations. Il souligne que le signe de l'exponentielle est toujours positif, et le seul élément important pour déterminer le signe de la dérivée est le terme "-x + 1". Il en déduit un tableau de variations de la fonction f, montrant qu'elle est croissante puis décroissante avec un maximum atteint à 1. Les limites de la fonction sont également calculées pour montrer que la limite en moins l'infini est moins l'infini et la limite en plus l'infini est 0. Ensuite, l'orateur calcule la deuxième dérivée de f et trouve que c'est égal à 7 fois (x-2) fois e^(-x). Il note que l'exponentielle est toujours positive et donc, le signe de la dérivée dépend du signe de (x-2), ce qui est positif pour x>2 et négatif pour x<2. Il conclut que le point x=2 est un point d'inflexion et utilise la formule f(2) pour trouver les coordonnées de ce point. Il explique également que visuellement, un point d'inflexion se distingue par un changement de pente avant et après le point. Enfin, il fait le lien avec les points d'inflexion souvent observés dans des domaines tels que la physique, comme dans le cas d'une courbe de titrage. Cette méthode sur la convexité et les points d'inflexion est la dernière thématique traitée dans le cours. Des questions supplémentaires peuvent être consultées dans la FAQ.

Convexité étude COMPLETE

Aucun résumé n'est disponible pour cette vidéo

Fonctions cubes et convexité

Dans ce cours, nous étudions un exercice qui présente plusieurs paramètres (A, B, C, D) et cherche à montrer un résultat général sur les fonctions x³. Cet exercice est intéressant car il essaie de généraliser des résultats intuitifs concernant les fonctions x³. Nous commençons par analyser la convexité de la fonction f en fonction des valeurs de A. Pour cela, nous calculons la dérivée seconde, f''(x), et la dérivée première, f'(x). Nous remarquons que le signe de f''(x) dépend de la valeur de A. Si A est positif, la fonction est d'abord concave puis convexe. Si A est négatif, la fonction est d'abord convexe puis concave. Nous concluons donc que lorsque A est positif, la fonction f est convexe si et seulement si x > -2B/3A. Lorsque A est négatif, la fonction f est convexe si et seulement si x < -2B/3A. Il est important de faire attention à ne pas confondre ces deux cas. Nous poursuivons l'étude en montrant quels sont les points d'inflexion de la fonction f. Un point d'inflexion est un point où la courbe change de convexité. Nous démontrons que quel que soit le signe de A, la courbe admet un point d'inflexion en abscisse -6B/3A. Enfin, nous appliquons ces résultats à un exemple concret qui nous montre qu'un point donné appartient à la courbe de la fonction f. Nous utilisons les résultats précédents pour montrer que ce point est bien un point d'inflexion de la courbe. En conclusion, cet exercice nous permet de mieux comprendre les propriétés de convexité et de concavité des fonctions x³ en fonction des valeurs de A. Il est important de bien distinguer les différents cas et de structurer notre raisonnement pour éviter les erreurs.