Cours de Limites des Fonctions en Ligne par les Meilleurs Professeurs - Limites des Fonctions

Introduction Convergence

Dans ce nouveau sous-chapitre sur les limites de fonctions, on va aborder des concepts pratiques. Il sera important de connaître par cœur certains tableaux de fonctions de référence, notamment la limite de 1 sur x en plus infini. On étudiera également comment combiner des limites, par exemple, si la fonction f tend vers 1 et la fonction g tend vers 2, quelle est la limite de f plus g ? Il y aura des règles générales à connaître ainsi que des cas particuliers appelés les formes indéterminées, pour lesquels il n'y aura pas de règles préétablies. On étudiera aussi des théorèmes de convergence, similaires à ceux déjà vus pour les suites. Le théorème des gendarmes, par exemple, où deux fonctions encadrent une troisième fonction et la conduisent vers la même limite. Il y aura également le théorème de comparaison pour les limites infinies, qui permet de déterminer si une fonction est plus grande qu'une autre en se basant sur leurs limites respectives. On abordera également la croissance comparée, en se concentrant principalement sur l'exponentiel et sa comparaison avec des polynômes. On verra aussi comment gérer les limites des fonctions composées, en décomposant les fonctions complexes en sous-blocs. En résumé, il sera nécessaire de connaître les tableaux de référence pour les fonctions, les opérations sur les limites, les formes indéterminées, les théorèmes de comparaison, de convergence et de croissance comparée, ainsi que la méthode pour gérer les formes indéterminées. Si on maîtrise ces points, on sera prêt à aborder les problèmes de limites de fonctions.

Tableaux : fonctions de référence

Dans cette vidéo, le cours aborde les notions de limites et de règles de combinaison des fonctions de référence. Il commence par évoquer la fonction 1/x, dont la limite est plus l'infini lorsque x tend vers 0 du côté positif, et moins l'infini lorsque x tend vers 0 du côté négatif. Ensuite, les limites des fonctions x^n, où n est un nombre entier positif, sont abordées. On observe que ces fonctions tendent toutes vers plus l'infini lorsque x devient très grand. Cependant, si n est impair, la fonction tend vers moins l'infini lorsque x devient très petit. Ensuite, l'exponentielle et la racine sont étudiées. L'exponentielle de x tend vers plus l'infini lorsque x tend vers plus l'infini, et vers 0 lorsque x tend vers moins l'infini. La racine de x tend vers 0 lorsque x tend vers 0, et 1/racine de x tend vers 0 lorsque x tend vers plus l'infini et moins l'infini. Ces notions sont illustrées à l'aide de graphiques, facilitant leur compréhension. Il est important de retenir ces différentes limites lors de résolutions d'exercices, afin de ne pas se tromper dans les calculs. Le cours se termine en invitant les spectateurs à poser leurs questions dans la FAQ.

Tableaux : combiner des limites

Ce cours aborde les limites de Fonctions. Lorsque deux fonctions, f et g, tendent vers les limites L et L', le produit de ces limites est L*L'. Si L est fini alors que la limite de g est soit +infini ou -infini, la limite de la multiplication est soit +infini ou -infini selon le signe de L. Pour les formes indéterminées, il n'y a pas de règle qui s'applique tout le temps. Les deux formes indéterminées à retenir sont 0 fois l'infini et plus l'infini plus moins l'infini. Les fonctions peuvent être combinées en quotient, f/g, et si les deux fonctions tendent vers des limites L et L', la limite du quotient est L/L'. Lorsque le quotient est 0 sur 0, toutes les réponses sont possibles. Lorsque le quotient est plus l'infini sur plus l'infini, toutes les réponses sont possibles également.

Comparaison et encadrement

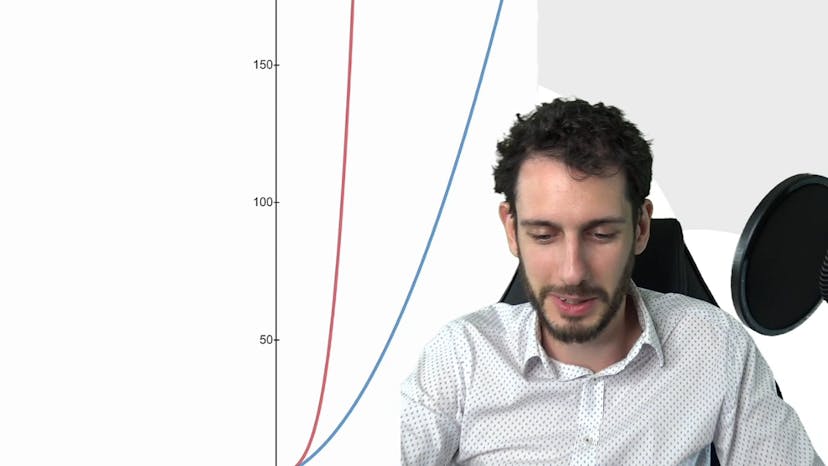
Ce cours traite de deux théorèmes qui permettent de comparer et d'étudier des fonctions de manière efficace, sans les étudier en détail. Le premier théorème est celui de la comparaison, qui dit que si une fonction f tend vers l'infini et qu'une autre fonction g est plus grande que f, alors f va pousser g vers l'infini. Le théorème d'encadrement, également appelé "théorème des gendarmes", est le second théorème présenté. Il stipule que si deux fonctions f et h encadrent une fonction g et tendent toutes deux vers la même limite, alors g tend également vers cette même limite. Le cours utilise des exemples pour illustrer ces théorèmes, notamment avec des graphiques pour mieux visualiser les concepts. Ces théorèmes sont particulièrement utiles pour résoudre des exercices de mathématiques impliquant des limites de fonctions.

Croissance comparée exp et ln

La croissance comparée est la théorie selon laquelle l'exponentielle l'emporte sur n'importe quelle puissance de x. En d'autres termes, si vous divisez E2x par x puissance n, la limite est toujours l'infini. L'exponentielle domine complètement sur les x puissances n. La propriété des puissances est utilisée pour appliquer cette théorie à l'exponentielle. On utilise également un changement de variable pour démontrer que la quantité tend vers 0 lorsque x tend vers moins l'infini. Cette méthode peut également être utilisée pour trouver des solutions simples à certains calculs de limites.

Limite des fonctions composées

Ce cours parle des limites de fonction, plus précisément de la composition de fonctions. L'exemple donné est celui de la limite de la racine de 1+ex lorsque x tend vers l'infini. Pour trouver cette limite, on décompose la fonction en deux parties: 1+ex et la racine de cette fonction. On utilise ensuite un théorème mathématique qui nous autorise à faire cette composition. La limité de la racine est prouvée en utilisant le comportement de la fonction racine envers la limite de 1+ex. Le théorème stipule que si la limite de f(x) tend vers b et que la limite de g(x) tend vers 1 quand f(x) tend vers b, alors la limite de g(f(x)) tend vers 1. En résumé, ce cours explique comment utiliser la composition de fonctions pour trouver des limites, en utilisant un théorème mathématique.

Forme indéterminée : utilisation du terme plus haut degré

La méthode pour déterminer les limites infinies des polynômes et des fonctions rationnelles est de factoriser par le terme de plus haut degré, également appelé le terme de Claudegris. Cette technique permet de résoudre les indéterminations et déterminer la limite facilement. Pour les polynômes, on factorise par x^4 et on obtient 1+4/x-2/x^3, qui tend vers 0 en plus/moins infini, et donc la limite est plus infinie. Pour les fonctions rationnelles, on factorise le numérateur et le dénominateur par le terme de Claudegris, et on fait attention au signe. En cas d'erreur, il suffit de vérifier la factorisation. Cette méthode est simple et efficace et il est important de la maîtriser en s'entraînant.

Forme indéterminée : Méthode quantité conjuguée

La méthode de la quantité conjuguée est utilisée dans les cas où il y a des racines car celles-ci ne s'additionnent pas bien. Pour supprimer ces racines, on multiplie souvent par la quantité conjuguée. Par exemple, si une fonction a une forme indéterminée lorsque x tend vers 0, on peut utiliser la quantité conjuguée pour lever cette indétermination. Si la fonction présente une forme indéterminée en l'infini, on utilise également la quantité conjuguée pour faire apparaître un plus dans l'expression. En utilisant cette méthode, on peut supprimer les racines et lever l'indétermination, ce qui permet de déterminer la limite de la fonction.

Limites : la Croissance comparée

La croissance comparée est une méthode utile pour étudier les fonctions. Elle consiste à comparer les croissances de différentes fonctions pour déterminer leur comportement en cas d'extrêmes. Dans ce cours, on étudie deux fonctions, E de X sur X et H, en utilisant la croissance comparée. La première fonction tend toujours vers plus infini, même si N est très grand. La seconde fonction est plus complexe mais on peut utiliser un changement de variable pour la ramener à la croissance comparée de référence. En général, l'exponentielle l'emporte sur toutes les puissances de X, tandis que le logarithme perd. Il est important de retenir ces références pour pouvoir lever la détermination facilement.

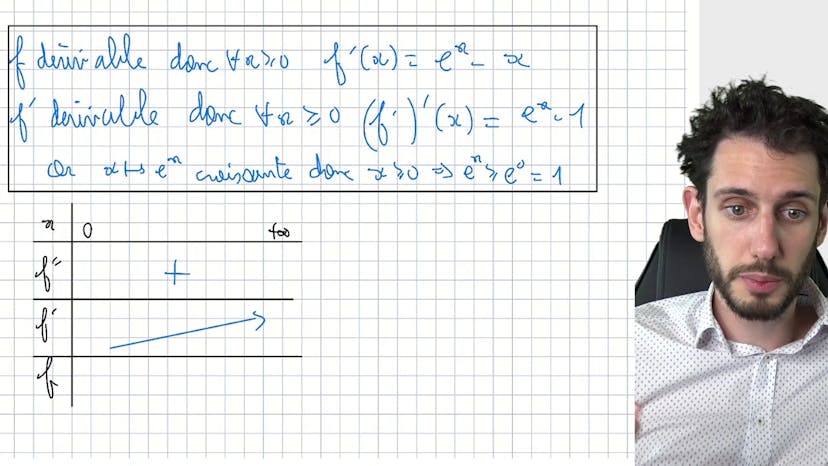
Double racine

Bonjour à tous ! Aujourd'hui, je vais vous résumer ce cours sur les limites de manière SEO friendly. Dans cet exercice de difficulté intermédiaire, nous devons étudier les limites. Tout d'abord, nous devons montrer que la fonction f est définie sur l'ensemble des réels. Pour cela, nous devons vérifier que les racines de la fonction sont positives ou nulles. Ensuite, nous devons étudier le tableau de variation de la fonction f. Pour pouvoir le faire, nous devons justifier la dérivabilité de f sur l'ensemble des réels. Puis, nous devons calculer la dérivée de la fonction f en utilisant la composition. Nous constatons que la dérivée est toujours positive, ce qui signifie que la fonction est strictement croissante. Enfin, nous devons étudier les limites de la fonction f. En utilisant la composition, nous montrons que la limite de f tend vers l'infini lorsque x tend vers l'infini et que la limite de f tend vers zéro lorsque x tend vers moins l'infini. Pour conclure, nous pouvons tracer le graphe de la fonction f en utilisant des valeurs remarquables. Voilà pour ce résumé SEO friendly de ce cours sur les limites. Merci d'avoir suivi !

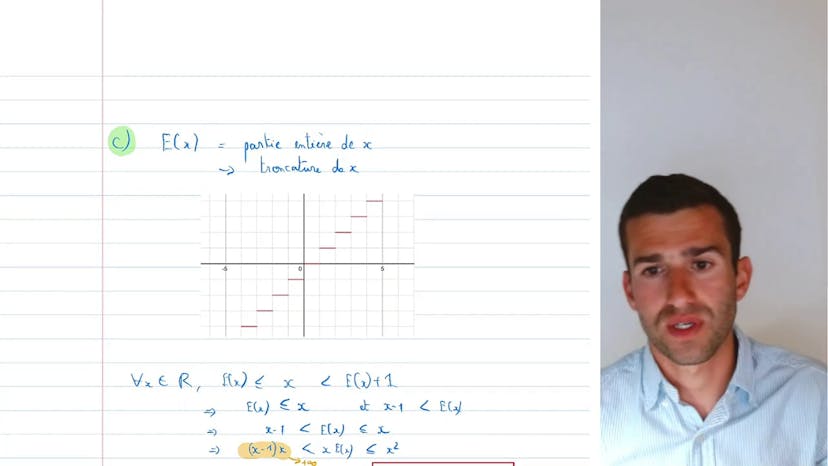
Calculs de limites complexes

Dans cette vidéo, le professeur explique comment résoudre cinq exemples de limites mathématiques complexes, destinées aux étudiants de niveau terminale++ et de préparation. Le premier exemple implique des racines et l'utilisation de quantités conjuguées pour simplifier l'expression, avec une astuce consistant à factoriser par le terme de plus haut degré. Le deuxième exemple implique des taux d'accroissement et la dérivée pour résoudre l'expression indéterminée, tandis que le troisième exemple utilise la partie entière pour encadrer l'expression afin de résoudre la limite. Le quatrième exemple utilise de nombreuses racines et une quantité conjuguée pour simplifier l'expression, tandis que le cinquième exemple divise l'expression en deux parties et utilise les taux d'accroissement pour résoudre l'expression indéterminée, en trouvant les limites des deux parties séparément.

Intro Convergence

Les théorèmes de convergence sont utilisés pour analyser des suites mathématiques complexes qui peuvent sembler difficiles à comprendre. Les deux théorèmes principaux sont le théorème de comparaison et le théorème de gendarme, qui ont des applications spécifiques pour montrer que les suites convergent ou divergent. Les suites minorées, majorées et bornées sont également définies, ce qui conduit au théorème de convergence monotone, important pour les mathématiques de niveau avancé. Les méthodes comprennent la gestion de sinus de n, de moins-un puissance n, et les suites homographiques, qui tombent souvent dans les examens.

Encadrer sin(n)

Dans cette vidéo, nous allons étudier deux exemples de suites en utilisant les théorèmes de convergence. Le premier exemple concerne la suite u_n = n + 2 * sin(n). Nous devons montrer que pour tout entier n, u_n est supérieur à n - 2. Pour encadrer la fonction sinus, nous savons que le sinus est toujours compris entre -1 et 1. En multipliant par 2, nous obtenons une valeur positive. En ajoutant n, nous obtenons finalement que u_n est supérieur à n - 2. Bien que cette partie de l'inéquation ne soit pas importante, elle est vraie. Ce qui nous intéresse vraiment est le fait que u_n est supérieur à n - 2. Comme n - 2 tend vers plus l'infini, et que u_n est plus grand qu'une suite telle que n - 2, nous pouvons conclure que u_n tend vers l'infini. Le deuxième exemple concerne la suite v_n = -n^2 + (-1)^n. Encore une fois, nous devons encadrer la puissance (-1)^n, qui est toujours entre -1 et 1. Le terme (-1)^n n'aura pas beaucoup d'importance, car il va alterner entre -1 et 1. Le terme dominant est n^2, qui tend vers moins l'infini. En encadrant la suite, nous obtenons que v_n est inférieur à une suite qui tend vers moins l'infini. En factorisant le terme dominant, nous obtenons v_n = n^2 * (-(1/n) + 1/n^2). La partie à droite tend vers 1, et la partie à gauche tend vers moins 1. Donc v_n tend vers moins l'infini. En utilisant l'encadrement, nous avons montré que les deux suites étudiées tendent toutes les deux vers l'infini et moins l'infini, respectivement.

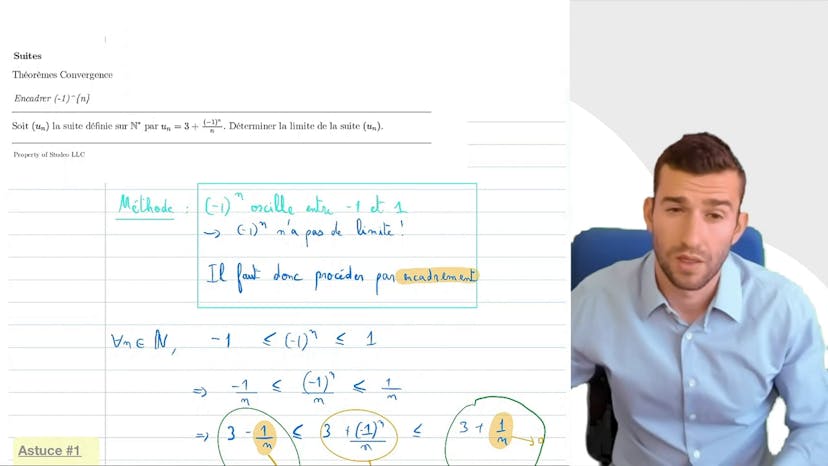
Encadrer (-1)^n

Dans ce cours, on étudie une suite qui contient des termes de la forme "-1 puissance n sur n". Grâce à une analyse asymptotique, on peut voir que cette suite tend vers 3. Pour prouver cela, on utilise la méthode de l'encadrement en multipliant l'expression par un nombre positif, et en ajoutant 3. On arrive à obtenir une expression qui encadre la suite entre 3 moins un sur n et 3 plus un sur n. En utilisant le théorème d'encadrement, on peut prouver que la suite converge vers 3. Cette méthode est très puissante car elle permet non seulement de prouver la convergence, mais aussi de trouver la limite.

Exo TRÈS classique

Dans cette méthode de convergence de suites, on étudie des suites sous forme de fonctions rationnelles, où le degré du numérateur est égal au degré du dénominateur. La limite est le quotient des coefficients dominants de chacun des polynômes. On s'intéresse aux résultats préliminaires comme la majoration, la croissance, et on en déduit la convergence avec les théorèmes de convergence. Pour étudier la monotonie d'une suite, on peut utiliser la méthode du quotient U n+1/U n. On ajoute ensuite les résultats préliminaires pour montrer la convergence. Les exemples présentés montrent comment majorer une suite et déduire la convergence en étudiant la croissance de U n, mais la limite ne sera pas toujours le majorant.

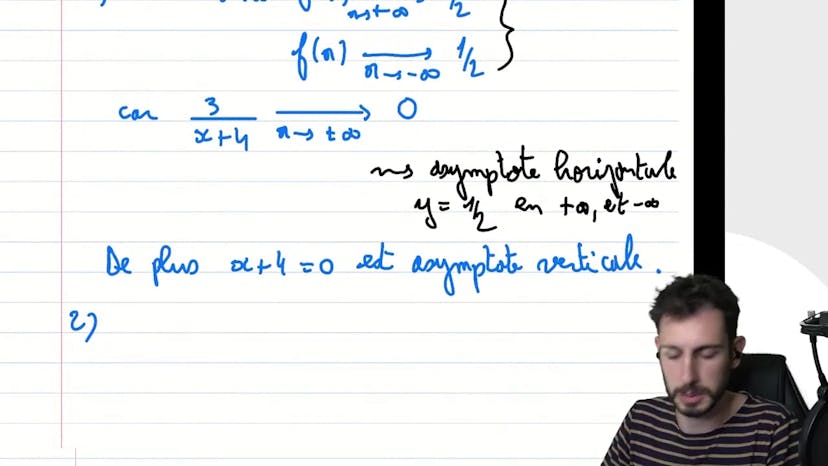
Asymptote et position relative

En étudiant une fonction classique, l'exercice porte sur l'étude de position relative et des asymptotes. Le réflexe immédiat est de factoriser f2x en bas par 2xx plus 4. Pour trouver la limite en plus et moins à l'infini, on peut considérer que pour des valeurs très élevées de x, une constante n'affecte pas grand-chose. Ainsi, f2x est approximativement égal à x sur 2x, ce qui fait 1,5. Ensuite, on peut réécrire la fonction homographique avec un polynôme de degré 1 pour le numérateur et le dénominateur. Il est utile de bien connaître cette technique pour trouver les éléments clés du comportement asymptotique. En utilisant cette écriture, on peut trouver les deux asymptotes de la fonction et résoudre la question 1. Pour la question 2, il faut trouver la position relative de CF par rapport à l'asymptote horizontale en faisant la différence des expressions de la fonction et de l'asymptote. En résumé, il est important de savoir reconnaître rapidement les asymptotes et de connaître la technique pour réécrire une fonction homographique.

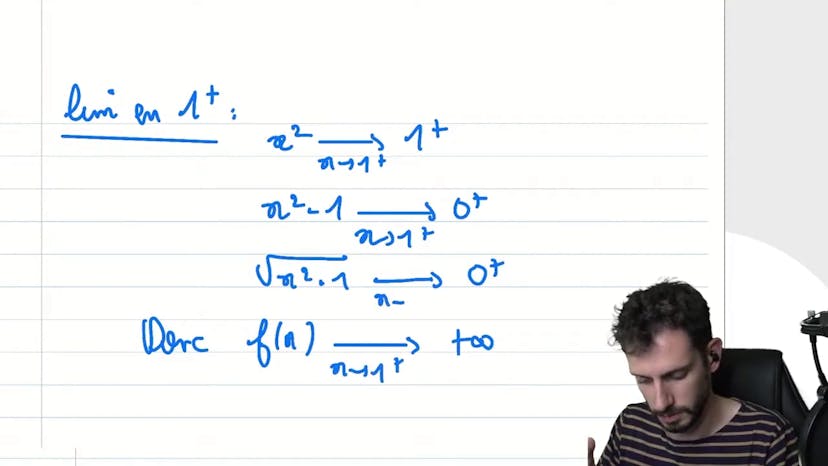
Étude TRES complète

Ce cours traite de la résolution d'une expression complexe en mathématiques. Pour trouver les valeurs de f, il est important de garder une expression positive ou nulle sous la racine, et d'éviter les divisions par zéro. Il est conseillé de vérifier la parité de la fonction afin de simplifier les calculs. En utilisant cette méthode, il est possible de trouver les limites de la fonction, en se basant sur l'infini et les bornes de DF. Les asymptotes sont également déterminées, en utilisant les limites précédemment calculées.

Asymptote oblique

En résumé, l'asymptote oblique est une droite de la forme AX plus B qui est approchée plus ou moins à l'infini. Bien que hors programme, il est important d'essayer les exercices qui impliquent des asymptotes obliques car il peut être difficile de les résoudre en terminale. La simplification en fractions est cruciale pour simplifier les expressions. Pour la dérivabilité d'une fonction, si elle n'a pas de racines ou de valeur absolue, alors elle est dérivable. Pour l'étude des variations et limites d'une fonction, il faut calculer les limites au bord de l'intervalle, vérifier la parité de la fonction et la dérivée. L'analyse de la position relative entre deux expressions est l'analyse du signe de la différence entre les deux expressions, qui doit être vérifiée pour l'étude de la position relative.

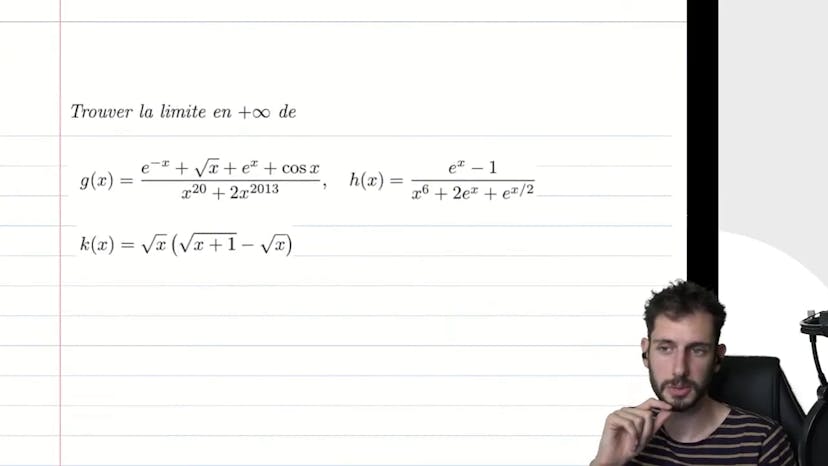
Croissance comparée plus lourde

Ce cours explique comment utiliser la croissance comparée pour trouver le petit h de x en gros. Pour simplifier, on compare E de x avec n'importe quelle puissance, en mettant en facteur E de x. On obtient 1-E de x, qui est facile à gérer. L'exercice tend vers 0 quand x tend vers l'infini, avec quelques nuances à prendre en compte. En résumé, ce cours montre une méthode utile pour trouver le terme dominant en mathématiques.

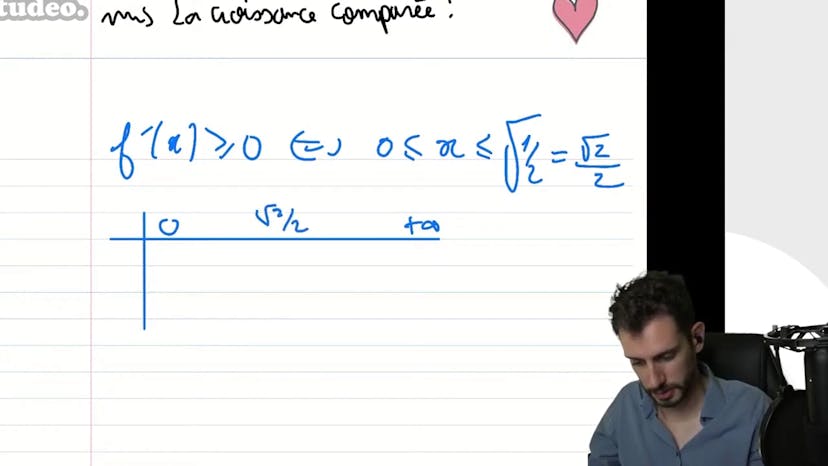
Difficile : BAC 2009

En bref, ce cours porte sur l'étude de fonction complète d'un examen de mathématiques de 2009. Il faut d'abord trouver la limite de la fonction à l'infini, ce qui nécessite l'utilisation de la croissance comparée pour comparer l'exponential et les puissances de x. Ensuite, il faut montrer que la fonction admet un maximum, ce qui nécessite de calculer la dérivée et d'analyser ses changements de signe. Enfin, on peut déterminer la valeur de la fonction au maximum, qui est égale à racine de 2 sur 2 fois exponentielle de moins 1 sur 2.

Exp : indéterminée en -∞

Dans cet exercice, on nous donne une fonction F2X et on nous demande de déterminer sa limite en plus l'infini, sa courbe CF comme asymptote horizontale et ses variations de f'E2X. Tout d'abord, on applique notre maîtrise des puissances pour simplifier la fonction F2X. Ensuite, on remplace petit x par moins grand x sur E de grand x, et on utilise des formules simples pour trouver la limite de la fonction. On en déduit que la courbe CF a une asymptote horizontale. Pour la variation de f'E2X, on calcule la formule du produit et on en déduit un petit tableau de variations. Finalement, on retrouve les limites que nous avions trouvées précédemment. La limite de f'F en plus l'infini est un plus 1, donc elle admet une asymptote horizontale y égale 1.

Vers la SUP : Quantité conjuguée

Dans cet exercice, il y a une somme finie de n termes avec x qui tend vers l'infini. Il est important de remarquer que c'est x qui tend vers l'infini et non pas n. Il y a des racines avec un signe moins, il s'agit de la méthode de quantité conjuguée à appliquer. Il y a n termes dans la somme qui sont compensés par n termes ailleurs. En utilisant cette méthode, il est possible de réécrire la somme en utilisant chaque racine avec un petit compagnon. En multipliant chaque terme par quantité conjuguée, on obtient une identité remarquable qui tend vers 0 lorsque x tend vers plus l'infini. La réponse est donc que la somme tend vers 0. Pour résoudre cet exercice, il est important de dépasser ses peurs et ses stress, analyser calmement la situation en se rappelant des méthodes et des astuces du cours.

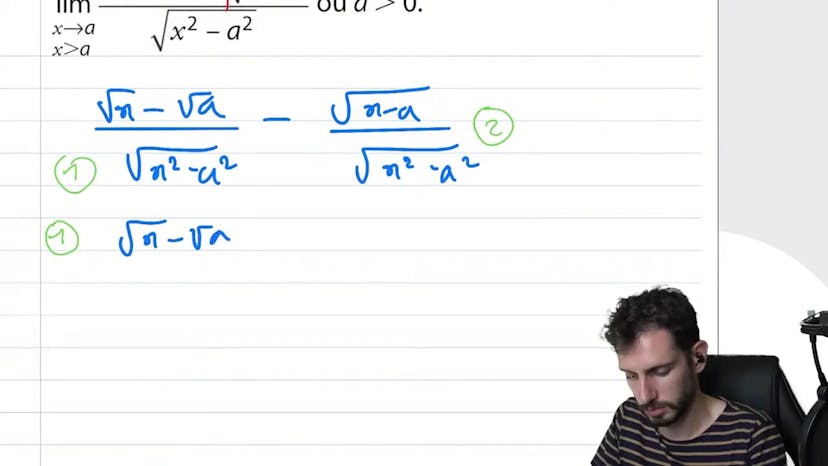
Quantité conjugée piégeuse

Le cours traite des quantités conjuguées et comment les utiliser correctement pour éviter les erreurs. L'auteur donne un exemple et explique pourquoi une certaine approche ne fonctionne pas. Il propose une solution en séparant la fraction en deux parties et en utilisant une quantité conjuguée pour simplifier l'expression. Ensuite, l'auteur gère chaque partie séparément et fait les calculs nécessaires pour arriver à la fonction finale. La fonction finale est donnée sous une forme simple et optimisée pour le SEO.

Théorème de comparaison - Illustration

Le théorème de comparaison en mathématiques permet d'économiser du temps et des efforts lors des démonstrations de suites. En effet, si l'on peut comparer une suite complexe à une autre plus simple et que cette dernière tend vers l'infini, alors nous pouvons conclure que la première suite aura le même comportement. Ce théorème est utile quand une suite est compliquée à démontrer et qu'on peut la comparer à une autre plus simple. Ainsi, le théorème permet de passer outre les démonstrations complexes en utilisant des suites plus simples. Dans la prochaine vidéo, nous verrons comment ce théorème peut être utilisé.

Théorème de comparaison - démonstration

Ce cours explique comment démontrer le théorème de comparaison en utilisant la divergence vers plus infini. Pour cela, il faut revenir à la définition de TvPi pour une suite et traduire la limite de Un égale plus infini. Ensuite, on peut conclure que Vn est plus grand ou égal à Un, plus grand ou égal à A pour tout A positif et N plus grand ou égal à un certain grand N de la suite. En résumé, cette démonstration permet d'éviter l'utilisation des démonstrations en epsilon ou en grand A, et de simplifier les exercices de comparaison.

Théorème des gendarmes

Le théorème d'encadrement, ou théorème des gendarmes, permet de montrer qu'une suite va tendre vers un réel fini en encadrant la suite entre deux autres suites convergentes vers la même limite. Le recours à ce théorème combiné au théorème de comparaison peut permettre d'accéder à des résultats sur les suites sans se préoccuper des définitions formelles d'epsilon et de A. Pour illustrer le théorème d'encadrement, on peut prendre l'exemple de la suite sinus s sur n encadrée par les suites des 1 sur n et des "-1 sur n". Si deux suites ordonnées convergent, alors leurs limites seront également ordonnées. Ce théorème est utile en mathématiques même si toutes les situations ne sont pas aussi simples à résoudre que celle de l'exemple.

Suite majorée, minorée & Th de convergence monotone

Dans ce cours, le professeur explique les concepts de majoration, de minoration et de bornage des suites. Une suite est dite majorée lorsqu'elle est bloquée par une certaine valeur et ne peut pas dépasser cette valeur. Il peut y avoir plusieurs majorants pour une suite. De même, une suite est dite minorée lorsqu'elle ne peut pas descendre en dessous d'une certaine valeur. Une suite est dite bornée lorsque elle est à la fois majorée et minorée. Le professeur illustre ces notions à l'aide de quelques exemples de suites bornées. Il mentionne le théorème de convergence monotone, qui associe le fait d'être croissante à celui d'être majorée. Ce théorème permet de conclure que si une suite est croissante et majorée, alors elle converge. Cependant, il précise que ce théorème ne donne pas la valeur de la limite de la suite. Le professeur présente également la version du théorème de convergence monotone pour les suites décroissantes et minorées, ainsi que pour les suites croissantes et non majorées, et les suites décroissantes et non minorées. Il insiste sur le fait que la réciproque du théorème de convergence monotone est fausse, c'est-à-dire que converger ne signifie pas forcément être croissante majorée ou décroissante minorée. Il donne des contre-exemples pour illustrer ce point, notamment la suite sinus sur n qui converge vers 0 mais oscille de manière "moche". Enfin, il conclut en soulignant l'importance de ne pas se laisser piéger par des fausses idées sur les suites qui convergent. N'hésitez pas à consulter la FAQ ou à discuter avec les autres étudiants si vous avez des questions.

Th convergence monotone - démo

Le théorème de convergence monotone prouve que toute suite croissante et non majorée tend vers l'infini. Il suffit de trouver un certain rang à partir duquel la suite est toujours au-dessus d'un nombre fixe A. Comme la suite n'est pas bloquée, il existe un anti-naturel P où la suite dépasse A. En combinant cela avec le fait que la suite est croissante, on peut montrer que pour tout A fixé, la suite finit toujours par être au-dessus de ce A. Cela prouve la convergence monotone.

Intro Convergence

Dans ce cours sur les théorèmes de convergence, on parle de suites qui peuvent être difficiles à gérer et qui semblent inexcessibles. Cependant, certaines de ces suites sont en réalité assez proches de zéro. On peut donc avoir l'intuition que ces suites vont converger vers zéro. Pour illustrer cela, le professeur montre un graphique montrant la fonction sin(x) ainsi que les différents points de la suite en question, qui convergent effectivement vers zéro. En termes mathématiques, les théorèmes de convergence nous permettent d'analyser ces suites en utilisant d'autres suites plus simples et classiques. Deux théorèmes importants pour cela sont le théorème de comparaison, qui permet de montrer qu'une suite tend vers l'infini, et le théorème de gendarme, qui permet de montrer qu'une suite tend vers une limite finie. On étudiera également les notions de suites minorées, majorées et bornées, ainsi que le théorème de convergence monotone, qui est essentiel en terminale. En termes de méthodes, on apprendra à gérer les sinus de n, les termes du type (-1)^n, et les suites homographiques, qui sont fréquemment rencontrées dans les exercices. Ce cours est accessible et clair, contrairement aux définitions de limites qui peuvent sembler plus compliquées. N'hésitez pas à poser vos questions dans la FAQ si vous avez besoin de précisions. La prochaine vidéo portera sur le théorème de comparaison.

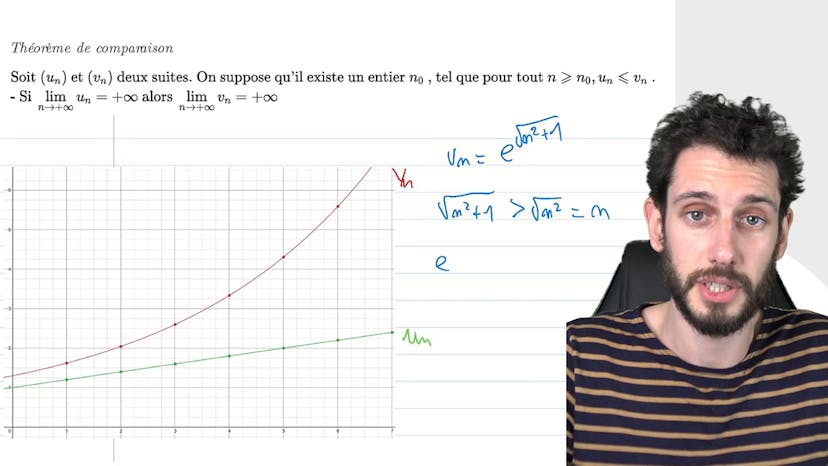
Théorème de comparaison - illustration

Le théorème de comparaison en mathématiques est un outil puissant qui permet d'économiser beaucoup d'efforts lors des démonstrations. Il consiste à comparer une suite complexe Vn à une suite plus simple Un, et si Un tend vers l'infini, alors Vn tendra également vers l'infini. Cela permet d'éviter de devoir manipuler des expressions compliquées et de résoudre des problèmes complexes. Par exemple, si on a la suite Vn définie comme l'exponentielle de la racine de n² plus 1, qui est difficile à gérer, on peut trouver une suite Un plus simple, comme la suite racine de n², et comparer les deux. En utilisant le fait que l'exponentielle est une fonction croissante, on peut conclure que Vn sera plus grand que Un, et donc Vn tendra vers l'infini. Ainsi, on évite de devoir étudier en détail la suite Vn et de faire de nombreuses manipulations complexes. C'est la beauté du théorème de comparaison en mathématiques.

Théorème des gendarmes

Le théorème de comparaison permet de démontrer que, si une suite VN tend vers l'infini, en la comparant à une suite UN plus petite et plus simple. Le théorème d'encadrement, également appelé théorème des gendarmes, est l'équivalent pour une limite finie. Il permet de montrer qu'une suite tend vers un réel fini en étant "prisonnière" entre deux autres suites convergentes vers la même limite. Ce théorème est très utile pour obtenir des résultats sur les suites sans avoir à se soucier des définitions formelles d'ε et d'A. Pour illustrer ce théorème, on prend l'exemple de la fonction sinus, qui converge vers 0. On encadre la suite sinn/n entre -1/n et 1/n, qui convergent toutes les deux vers 0. En utilisant le théorème des gendarmes, on peut en déduire que la suite sinn/n converge également vers 0. Ce théorème permet donc de simplifier les calculs en encadrant des suites plus complexes entre des suites plus simples dont on connaît la limite. Cependant, il n'est pas toujours possible d'utiliser le théorème des gendarmes dans toutes les situations. Parfois, on dispose de moins d'informations et on peut donc affirmer moins de choses. Néanmoins, il existe d'autres propriétés des suites, comme le fait que si deux suites sont ordonnées et convergentes, alors leurs limites seront également ordonnées de la même manière. Cette propriété intuitive doit également être connue et comprise. En résumé, le théorème des gendarmes, ou théorème d'encadrement, permet de démontrer que si une suite est "coincée" entre deux autres suites convergentes vers la même limite, alors elle converge également vers cette limite. Ce théorème est très pratique pour simplifier les calculs et obtenir des résultats sur les suites.

Définitions + th de CV monotone

Une suite est dite majorée lorsqu'elle ne dépasse pas une certaine valeur. Elle peut avoir plusieurs majorants, c'est-à-dire plusieurs valeurs qui la bloquent par le haut. Une suite est minorée lorsqu'elle ne descend pas en dessous d'une certaine valeur. De même, elle peut avoir plusieurs minorants, c'est-à-dire plusieurs valeurs qui la bloquent par le bas. Lorsqu'une suite est à la fois majorée et minorée, on dit qu'elle est bornée. Le théorème de convergence monotone établit que si une suite est croissante et majorée, alors elle converge. De même, si une suite est décroissante et minorée, elle converge également. Si une suite croissante n'est pas majorée, elle tend vers plus l'infini, tandis qu'une suite décroissante non minorée tend vers moins l'infini. Il est important de noter que la réciproque du théorème de convergence monotone est fausse. Une suite peut converger sans être croissante ou décroissante. Par exemple, la suite sinus(1/n) converge vers 0, bien qu'elle oscille de manière irrégulière. Il est essentiel de bien comprendre ces concepts pour éviter de se tromper dans les exercices et les questions de cours.

Théorème de comparaison - Illustration

Le théorème de comparaison est un outil puissant en mathématiques qui permet d'éviter de nombreuses démonstrations fastidieuses. En bref, si une suite Vn peut être comparée à une suite plus simple, et que cette dernière tend vers l'infini, alors on peut conclure que Vn tend également vers l'infini. Ce théorème est pratique car il permet de traiter des suites compliquées et de les comparer à des suites plus faciles à étudier. Par exemple, si on souhaite démontrer que la suite Vn = exp(n² + 1) tend vers l'infini, on peut la comparer à la suite Un = exp(n), qui est simple et diverge vers l'infini. En utilisant le fait que l'exponentielle est une fonction croissante, on peut conclure que Vn sera plus grand que Un, et donc tendra également vers l'infini. Ainsi, grâce au théorème de comparaison, on peut faire des économies d'efforts en évitant de faire des démonstrations détaillées. Dans la prochaine vidéo, nous verrons la démonstration de ce théorème.

Théorème de comparaison - démonstration

Le cours explique comment démontrer le théorème de divergence en mathématiques, en utilisant une approche SEO-friendly. Le professeur commence par expliquer que malgré l'avantage de ce théorème de se passer des démonstrations en epsilon et en grand A, il est nécessaire de revenir à la définition pour la démontrer. Le professeur démontre ensuite que si la limite d'une suite tend vers l'infini, alors il existe un certain rang à partir duquel tous les éléments de cette suite sont plus grands qu'un certain nombre A positif. En utilisant cette information, le professeur conclut que pour tout A positif, il existe un certain rang à partir duquel tous les éléments de la suite sont plus grands que A. Finalement, le professeur résume cette démonstration en expliquant que pour tout A positif, il existe un certain rang à partir duquel tous les éléments de la suite sont plus grands que A, ce qui correspond à la définition de la divergence vers l'infini. En utilisant cette démonstration, il n'est plus nécessaire d'utiliser des démonstrations plus complexes avec des grands A et des petits epsilon.

Théorème des gendarmes

Le théorème d'encadrement, aussi appelé le théorème des gendarmes, est l'équivalent du théorème de comparaison pour les limites finies. Il permet de démontrer que si une suite est "encadrée" entre deux autres suites convergentes vers la même limite, alors cette suite sera également convergente vers cette même limite. Pour illustrer ce concept, prenons l'exemple de la suite sinus n sur n. Cette suite est un peu complexe à analyser directement, mais nous pouvons l'encadrer en utilisant les fonctions sinx sur x et les suites 1 sur n et -1 sur n, qui convergent toutes deux vers 0. En utilisant le théorème des gendarmes, nous pouvons donc conclure que la suite sinus n sur n converge également vers 0. Il est important de noter que le théorème des gendarmes n'est pas toujours applicable et que parfois nous avons moins d'informations pour pouvoir déduire autant. Cependant, une propriété importante à retenir est que si deux suites un et vn sont ordonnées, c'est-à-dire que un est toujours plus petit que vn, et que ces deux suites convergent, alors leurs limites seront également ordonnées de la même manière, la limite de un étant plus petite que la limite de vn. N'hésitez pas à poser des questions et à discuter avec d'autres étudiants pour clarifier des points.

Suites majorées, minorées & le th de convergence monotone

Aucun résumé n'est disponible pour cette vidéo

Théorème des gendarmes

Le théorème d'encadrement, également connu sous le nom de théorème des gendarmes, permet de montrer que si une suite est prise en sandwich entre deux autres suites qui convergent vers la même limite finie, alors elle converge également vers cette limite. Ce théorème peut être utilisé pour démontrer des résultats sur les suites sans avoir à s'embêter avec les définitions formelles. Dans l'exemple donné, la fonction sin(x) est tracée et semble converger vers 0. Cependant, la suite sin(n)/n est plus difficile à gérer. Pour simplifier, on peut encadrer sin(x)/x entre -1/x et 1/x. En traçant les deux fonctions, on constate qu'elles encadrent parfaitement la suite sin(n)/n. On sait que les suites 1/n et -1/n convergent vers 0, donc on peut conclure que la suite sin(n)/n converge également vers 0. Il est important de noter que même si le théorème des gendarmes peut être très pratique, il ne s'applique pas toujours et il est possible de dire moins de choses dans certaines situations. Cependant, une propriété importante à retenir est que si deux suites sont ordonnées (un toujours plus petit que vn) et qu'elles convergent, alors leurs limites respectives seront également ordonnées (la limite de vn sera plus petite que la limite de vn).

Suite majorée, minorée & Th de convergence monotone

Le cours aborde les définitions des concepts de majoration, minoration et bornitude pour les suites. On dit qu'une suite est majorée lorsque ses termes sont tous bloqués par une certaine valeur, et on dit qu'une suite est minorée lorsque ses valeurs ne peuvent pas descendre en dessous d'une certaine valeur. Une suite bornée est à la fois majorée et minorée. L'exemple d'une suite croissante 2-1/n est donné, montrant qu'elle est majorée par 2. D'autres exemples de suites majorées, minorées et bornées sont également donnés, montrant différentes variations de comportement. Le théorème de convergence monotone est introduit, qui établit une relation entre la croissance et la majoration d'une suite. Si une suite est croissante et majorée, alors elle converge. Cependant, il est souligné que ce théorème ne donne pas accès à la valeur limite de la suite. Il est nécessaire de faire une étude plus approfondie pour trouver la limite. Le cours aborde également les cas où une suite peut converger vers l'infini positif ou négatif, même si elle n'est pas croissante ou décroissante. Des exemples de suites qui tendent vers l'infini positif ou négatif sont donnés, illustrant que la réciproque du théorème de convergence monotone est fausse. En conclusion, il est souligné l'importance de ne pas se laisser piéger par de fausses idées sur la convergence des suites, et il est encouragé à poser des questions et à participer aux discussions avec les autres étudiants.

Th convergence monotone - démo

Le théorème de convergence monotone démontre que dans le cas d'une suite croissante non majorée, c'est-à-dire une suite qui n'est jamais bloquée, celle-ci tend vers l'infini. On va revenir à la définition formelle de la convergence vers l'infini et on va réaliser que c'est quasiment la même chose que cette définition formelle, donc la démonstration ne sera pas compliquée. On commence par fixer un A positif strict. L'objectif sera de montrer qu'il existe un rang à partir duquel tous les termes de la suite sont supérieurs à A. Ce qui signifie que tout A finira par être dépassé. Comme la suite UN n'est pas majorée, il existera donc un rang P tel qu'à partir de ce rang, UP sera plus grand que A. En combinant cela avec le fait que la suite est croissante, on peut affirmer que pour tout N supérieur à P, UN sera toujours plus grand que UP. Cela signifie donc qu'à partir de P, pour tout N supérieur à P, UN sera strictement supérieur à A. Ainsi, on a démontré que pour tout A fixé, il existe un rang à partir duquel tous les termes de la suite sont supérieurs à A. Cela confirme donc la convergence vers l'infini. Deux conclusions sont à retenir : la suite finit toujours par être au-dessus de tout A fixé et cela explique le concept de tendance vers l'infini. C'est tout pour cette démonstration, à la prochaine.

Encadrer sin(n)

Dans ce cours, nous étudions les fonctions sinus et moins 1 plus sin dans le contexte des théorèmes de convergence. Nous examinons la suite un = n + 2*sin(n) et montrons que pour tout n, un est supérieur à n-2. Pour cela, nous utilisons l'encadrement du sinus entre -1 et 1 pour obtenir un encadrement de un. Puisque le sinus n'a pas de limite définie, il est essentiel de l'encadrer. En multipliant le sinus par 2 (ce qui est positif) et en ajoutant n, nous obtenons un qui est supérieur à n-2. Bien que cette partie de l'inéquation ne soit pas notre objectif, elle est néanmoins vraie. En effet, un est compris entre n-2 et n+2. Nous nous intéressons principalement à la première partie de cette inéquation. Puisque n-2 tend vers l'infini et que un est supérieur à une suite qui tend vers l'infini, nous pouvons conclure, par comparaison, que un tend vers l'infini. Dans le deuxième exemple, nous considérons la suite Vn = -n^2 - n + (-1)^n. Encore une fois, nous utilisons l'encadrement de (-1)^n entre -1 et 1 car cette fonction n'a pas de limite. Nous remarquons que le terme dominant est n^2, alors que (-1)^n n'a qu'un rôle mineur. Nous faisons l'encadrement de Vn en ajoutant (-1)^n, puis nous obtenons une suite qui tend vers moins l'infini. En factorisant le terme de plus haut degré, nous obtenons Vn < n^2*(-1) + (-1/n) + (1/n^2). La partie de droite tend vers 1, alors que la partie avec le minus tend vers moins 1. Ainsi, n^2*(-1) - n + 1 tend vers moins l'infini. En utilisant la comparaison avec une suite qui tend vers moins l'infini, nous concluons que Vn tend vers moins l'infini. Ainsi, ces deux exemples illustrent l'utilisation de l'encadrement pour traiter des suites impliquant des fonctions sinus ou (-1)^n.

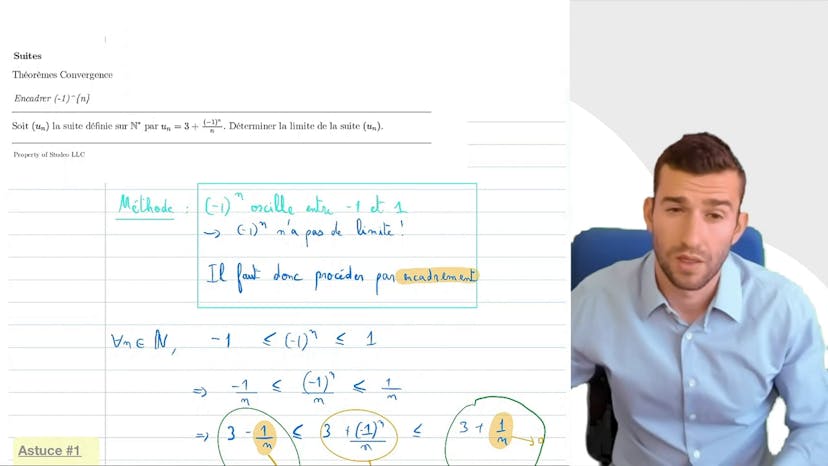
Encadrer (-1)^n

Dans ce cours, on étudie des suites où l'encadrement est nécessaire. Ces suites sont du type "(-1)^n/n" et n'ont pas de limite. Cependant, on peut les encadrer pour les analyser asymptotiquement. En utilisant cette méthode, on montre que la suite UN = 3 + (-1)^n/n tend vers 3. On utilise le théorème d'encadrement pour montrer cette convergence et trouver la limite. Le théorème d'encadrement est très puissant car il permet de prouver la convergence et de trouver la limite en même temps. Ici, par encadrement, on a prouvé que UN tend vers 3.

Exo TRÈS classique

Dans cette méthode, on étudie une suite qui est une fonction rationnelle de n, où le degré du numérateur est égal au degré du dénominateur. La limite de cette suite est le quotient des coefficients dominants des polynômes constituant le numérateur et le dénominateur. On s'intéresse aux résultats préliminaires tels que la majoration, la croissance et la convergence. Dans le premier exercice, on considère la suite Un = (n-1)/(n+4) et on veut montrer qu'elle est majorée par 1. Pour cela, on remarque que le numérateur est plus petit que le dénominateur si c'est plus petit que 1. On peut alors partir de -1, dire que -1 est plus petit que 4, ajouter n, et ensuite faire le quotient. Comme c'est positif, le signe ne change pas, donc on en déduit que Un est strictement inférieur à 1. Pour étudier la monotonie de la suite, on utilise généralement Un+1 - Un. On peut parfois utiliser le quotient, mais il faut vérifier certaines conditions, comme le fait que Un ne s'annule jamais et qu'elle ne change pas de signe. Si la suite est constituée de produits de quotients ou de factoriels, on peut étudier le quotient Un+1/Un. Dans ce cas, on peut dire que la suite ne change pas de signe à partir d'un certain rang, car on s'intéresse à ce qui se passe à l'infini. On peut également utiliser la méthode du quotient Un+1/Un pour étudier les variations de la suite. On fait la différence entre deux quotients et on simplifie au maximum en développant. On peut alors observer les termes qui se suppriment. Si tous les termes restants sont positifs, on en déduit que la suite est strictement croissante. Si la suite est croissante et majorée, on peut conclure qu'elle est convergente. Cependant, la méthode du quotient ne permet pas de connaître la limite de la suite. Enfin, les exemples donnés dans le texte montrent qu'il est possible de trouver un majorant de la suite, mais cela ne garantit pas que la suite converge vers ce majorant. Il est important de faire attention à cela lors de l'utilisation des théorèmes de convergence.

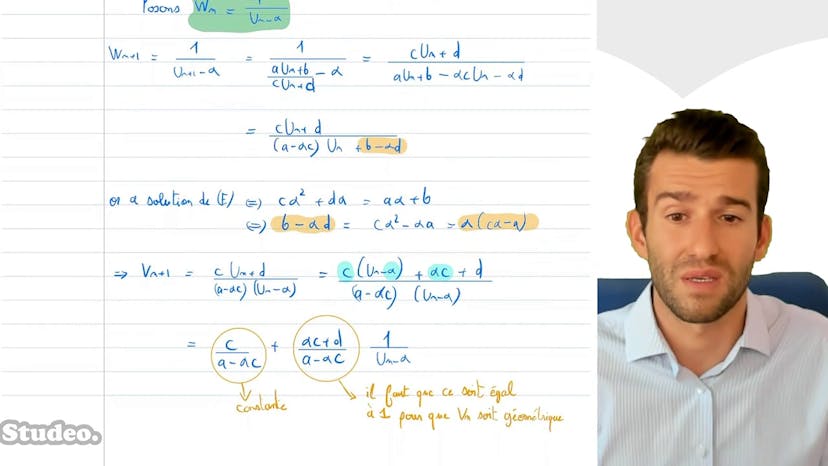
Suite homographique

Une suite homographique est une suite qui vérifie une relation de récurrence de la forme "un+1 = (aun + b)/(cun + d)". Il y a deux cas possibles : soit l'équation a deux solutions, auquel cas on pose une suite auxiliaire géométrique, soit elle a une seule solution, auquel cas on pose une suite auxiliaire arithmétique. En utilisant ces suites auxiliaires, on peut trouver l'expression de la suite homographique. Pour trouver l'expression de ces suites auxiliaires, on peut résoudre l'équation homographique et poser des suites auxiliaires en fonction des solutions trouvées. En utilisant différentes manipulations et simplifications, on peut obtenir l'expression de ces suites auxiliaires et remonter à l'expression de la suite homographique. En conclusion, les suites homographiques peuvent être résolues en posant des suites auxiliaires géométriques ou arithmétiques en fonction des solutions de l'équation homographique. Ces suites auxiliaires permettent de trouver l'expression de la suite homographique. Des exemples sont présentés pour illustrer le processus de résolution.

Encadrement

Dans ce cours, nous allons apprendre une astuce pour l'encadrement. Cette astuce est assez simple et rapide à utiliser, mais il est important de savoir la maîtriser car elle peut être utile dans certains exercices. La méthode consiste à utiliser deux suites de règles entre 0 et 1, telles que la limite entre un et vn en tant que produit tend vers 1. L'objectif est de démontrer que les suites un et vn convergent toutes les deux vers 1. Pour cela, nous allons prendre l'exemple de la suite un. Nous utilisons le fait que vn est compris entre 0 et 1, nous pouvons alors encadrer un en le limitant entre 1 et un-vn. En utilisant le théorème d'encadrement, nous concluons que un tend vers 1. Il est important de noter que cette astuce peut également être appliquée à la suite vn. Il s'agit donc d'une astuce rapide mais utile pour passer du produit de suite à l'une des deux suites. N'oubliez pas de bien maîtriser cette méthode car elle peut être fréquemment utilisée.

Suites adjacentes

Les suites adjacentes sont étudiées dans ce cours. Deux suites sont couplées et imbriquées l'une par rapport à l'autre. Une combinaison linéaire est utilisée pour simplifier le problème. On découvre que VN-UN est une suite géométrique de raison un tiers, avec un signe constant. On en déduit que UN et VN sont monotones et de sens de variation opposé. De plus, VN-UN tend vers zéro, ce qui montre que les deux suites sont adjacentes et convergent vers une limite commune L. En utilisant cette information, on obtient l'équation U0+V0=2L, ce qui permet de trouver la valeur de L. La subtilité est que cette fois-ci, c'est aux étudiants de trouver les combinaisons linéaires.

Série harmonique

Dans ce cours, nous allons étudier un exercice basé sur la série Harmonic. La première étape consiste à montrer que la série Harmonic diverge. Ensuite, nous allons examiner à quelle vitesse la série s'écarte de ln(2n+1). Nous verrons que cette suite converge vers une réelle constante, gamma, qui est la constante d'air. Cette deuxième partie est moins classique, mais tout aussi importante. Pour mieux comprendre la réponse à la question, nous allons utiliser une comparaison de séries intégrales. Nous encadrons l'intégrale de la fonction 1 sur x entre deux aires de rectangle. Nous prouvons ensuite rigoureusement cette comparaison en utilisant la décroissance de la fonction 1 sur x. Ensuite, nous démontrons que la suite harmonique converge vers plus l'infini en comparant les inégalités de gauche et de droite. Dans la deuxième partie du cours, nous étudions les suites h et v. En étudiant leur sens de variation, nous remarquons que h est décroissante et v est décroissante. Ensuite, nous montrons que la différence entre les deux suites tend vers 0. Cela nous permet de conclure que h et v convergent vers une même limite, gamma, qui est la constante d'air. Enfin, nous calculons la valeur de gamma, qui se situe entre 1,5 et 1, et nous déterminons à partir de quelle valeur de n la différence entre h et v devient inférieure à 10,2. Il est essentiel de maîtriser la première partie de l'exercice sans hésitation. Cette méthode vous permettra de résoudre des exercices similaires.