 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Introduction Limites
Lors de l'étude des limites de fonctions, on peut s'inspirer de ce qui a été fait pour les suites. Une suite converge lorsque ses termes semblent se rapprocher d'une valeur. Les fonctions sont plus complexes que les suites car elles portent sur l'ensemble des réels, contrairement aux suites qui ne portent que sur les entiers. Les fonctions peuvent avoir différents types de limites, comme se rapprocher d'un réel, tendre vers l'infini ou osciller. On utilise un vocabulaire plus étendu lorsqu'on parle de limites de fonctions. Les limites peuvent être étudiées en l'infini, c'est-à-dire lorsque la variable tend vers l'infini, ou en un réel particulier. Il y a également des cas où il n'y a pas de limite. Des exemples graphiques sont utilisés pour illustrer ces différents cas. On introduit également la notion d'asymptote, qui est une droite vers laquelle la fonction semble tendre. Dans ce chapitre, nous étudierons les définitions et les exemples de limites, ainsi que les méthodes pour les calculer. Nous utiliserons l'analyse graphique, la factorisation et les définitions pour déterminer les limites. Il faudra aussi connaître les concepts d'asymptotes horizontales et obliques.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

En l'infini, limites finies et infinies
La séquence présente deux définitions des limites lorsque x tend vers l'infini en mathématiques. La première définition concerne les fonctions qui tendent vers l'infini lorsque x devient de plus en plus grand. On dit qu'une fonction tend vers l'infini si, quel que soit le plateau Y choisi, la fonction finit toujours par dépasser ce plateau. La deuxième définition concerne les fonctions qui tendent vers un réel L. Dans ce cas, toutes les valeurs de la fonction finissent par être comprises dans un intervalle autour de L, peu importe la taille de cet intervalle. Ces définitions sont similaires à celles utilisées pour les suites. Il est important de préciser que lorsque x tend vers plus l'infini, afin de distinguer les autres valeurs de x. Les exemples graphiques sont présentés pour illustrer ces définitions. Il est conseillé de comprendre ces concepts, car ils sont utilisés dans des exercices mathématiques et peuvent rapporter des points précieux. N'hésitez pas à poser des questions si nécessaire.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Les asymptotes horizontales
Lorsque X tend vers l'infini, une asymptote est une droite vers laquelle la courbe de la fonction F se rapproche. Cela se produit lorsque la limite de F lorsque X devient très grand converge vers un réel appelé L. Il est important de rappeler qu'il existe une asymptote à la courbe de F et non à la fonction F elle-même. Une petite erreur courante à éviter est de dire que la droite se colle à la fonction F au lieu de dire qu'elle se colle à la courbe de la fonction F. Un exemple d'asymptote horizontale est une fonction de la forme 1/X, où la droite Y égale 3 est asymptote à la courbe de F. Il peut y avoir des asymptotes croissantes ou décroissantes selon le côté où la courbe se rapproche de la droite. Il est également possible d'avoir une asymptote pour des fonctions comme le sinus. L'asymptote est la droite vers laquelle la courbe de F se rapproche infiniment proche. C'est une notion liée à la limite et intuitive.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
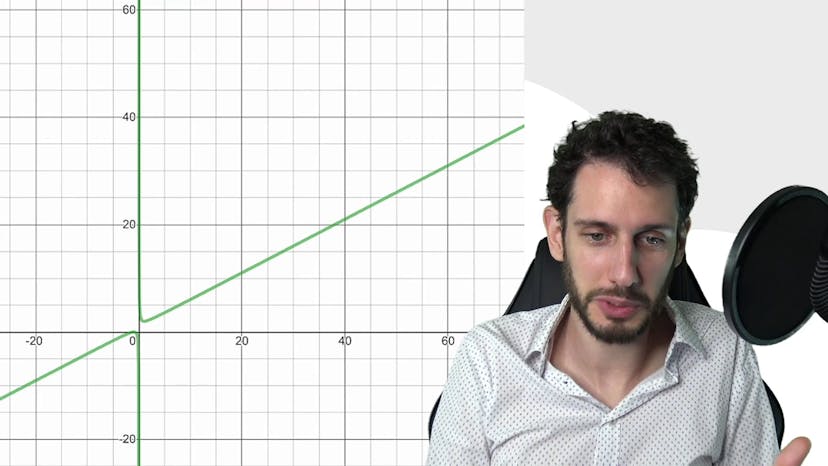
Bonus : Les asymptotes obliques
Dans ce cours, nous abordons le concept d'asymptote oblique qui se produit lorsque l'asymptote d'une courbe n'est plus horizontale mais inclinée. Nous considérons une fonction f définie sur un ensemble de définitions (df), dont la courbe cf représente la fonction f. Lorsque la différence entre la valeur réelle f2x et la droite ax + b tend vers 0, cela signifie que la courbe se rapproche de la droite oblique ax + b. Contrairement aux asymptotes horizontales où f2x tend vers une valeur réelle l, ici f2x tend vers plus l'infini car elle suit une droite affine. Il est important de savoir détecter et comprendre ce type de situation, car cela se produit fréquemment dans les exercices. Un exemple d'illustration est donné, montrant comment la courbe verte se rapproche de plus en plus de la droite rouge à mesure qu'on se rapproche de l'infini. Lorsque l'on dézoome, on constate que la courbe est pratiquement une droite. Dans certaines situations, cela peut également se produire de l'autre côté de la courbe. La différence entre les valeurs des courbes verte et rouge tend vers 0, indiquant un rapprochement. Ce cours a pour objectif de clarifier le concept d'asymptote oblique.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

En un point réel, limite infinie
Lorsqu'on parle de limite de fonction avec X qui tend vers un réel A, on distingue deux cas principaux :
1. La fonction F peut finir par partir vers plus ou moins l'infini.
2. La fonction F peut converger vers une valeur finie.
Dans le cas où la fonction F converge vers une valeur finie, cela signifie que la courbe de la fonction suit son cours normal et s'approche d'une valeur L. Cette notion est appelée la continuité.
Par exemple, la limite de X + 3 lorsque X tend vers 2 est égale à 5.
Cependant, il existe des cas plus complexes, comme celui de la fonction sinus X sur X où la limite en 0 est indéterminée (0/0). Dans ce cas, on exclut 0 de l'ensemble de définition de la fonction pour éviter une division par 0. Malgré cela, il est possible de démontrer que la limite de cette fonction en 0 est égale à 1.
En ce qui concerne la limite infinie, on peut l'aborder en utilisant la notion de plateau. Lorsque la fonction F tend vers plus l'infini, cela signifie que la fonction ne peut être bloquée par aucun plateau de données. Par exemple, si on prend une hyperbole, peu importe la taille du plateau choisi, la fonction finira par le dépasser lorsqu'on se rapproche de plus en plus d'une valeur donnée.
Si la limite à gauche ou à droite de F(x) lorsque X tend vers A est infinie, on parle d'une asymptote verticale en X égale à A.
En résumé, lorsque X tend vers un réel A, il peut y avoir plusieurs cas de limite de fonction, dont certains peuvent être représentés par des asymptotes verticales ou horizontales.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
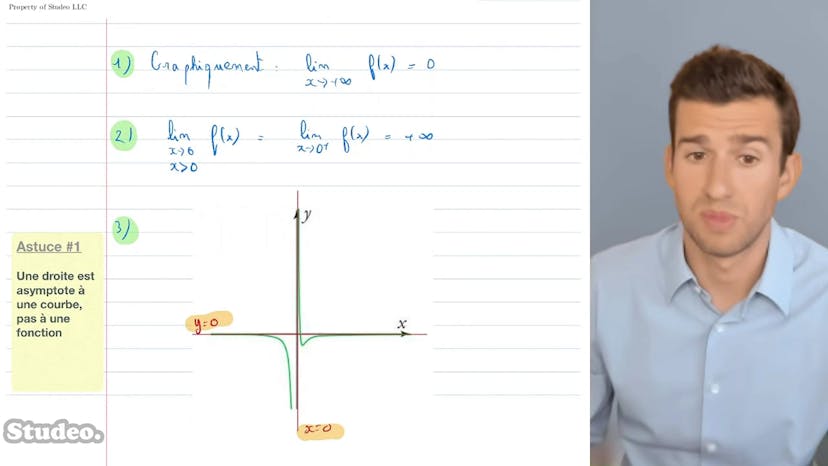
Analyse graphique
Bonjour à tous ! Dans ce cours, nous allons aborder la notion des limites des fonctions à travers une analyse graphique. Nous examinons une fonction tracée et tentons de déterminer ses limites. Lorsque nous observons le graphique, nous constatons que lorsque x tend vers l'infini, la fonction tend vers 0. C'est notre première observation. Ensuite, lorsque x tend vers 0 par une valeur positive, nous remarquons que la courbe s'élève vers l'infini. Cela nous conduit à conclure que la fonction admet deux asymptotes, une verticale en x=0 et une horizontale pour les valeurs positives et négatives infinies. Lorsqu'on nous demande les équations des asymptotes, nous savons que les droites horizontales sont de la forme y=a, tandis que les droites verticales sont de la forme x=a. Dans ce cas, l'équation pour l'asymptote horizontale est y=0 et pour l'asymptote verticale, c'est x=0. Une remarque importante à faire est qu'on parle d'une droite comme étant l'asymptote d'une courbe et non de sa fonction. Enfin, il est tout à fait possible qu'une droite soit asymptote en deux endroits, comme c'est le cas ici où l'asymptote horizontale est présente pour les valeurs positives et négatives infinies. Voilà pour cette méthode d'introduction. Si vous avez des questions, n'hésitez pas à les poser.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Calcul limite en un point fini par factorisation
Dans ce cours, nous allons apprendre une méthode pour calculer la limite d'une fonction lorsque l'on a une forme indéterminée. Dans ces cas-là, il est souvent possible de factoriser pour lever l'indétermination.
Dans le premier exemple, nous avons la fonction f(x) = x² - 2x / (x - 1). On peut remarquer que cette expression peut être simplifiée en utilisant l'identité remarquable (x - 1)² / (x - 1), ce qui donne x - 1. Ainsi, la limite de f(x) lorsque x tend vers 1 est 0, que ce soit à gauche ou à droite.
Dans le deuxième exemple, nous avons la fonction g(x) = (x² - 2x + 1) / (2x - 2). Nous pouvons simplifier cette expression en factorisant tout d'abord le numérateur par (x - 1)² et en factorisant ensuite par 2. Ainsi, g(x) peut s'écrire comme 2(x - 1)(x - 2). Pour trouver les racines de ce polynôme, nous pouvons utiliser la méthode classique du delta, qui nous donne les racines x1 = 1 et x2 = 2. En utilisant ces racines, nous pouvons factoriser g(x) en 2(x - 1)(x - 2). En simplifiant cette expression, nous obtenons (x - 1) / (2x - 2). Nous pouvons également remarquer que si nous avions testé la valeur 1 comme racine, nous aurions pu trouver directement la factorisation sans calculer le delta.
Ensuite, nous devons déterminer la limite de ces fonctions à droite et à gauche en 1. Pour f(x), la limite est de 1 des deux côtés. Pour g(x), quand x tend vers 1, la limite de x - 2 est -1, ce qui est différent de 0. Ainsi, la limite de g(x) quand x tend vers 1 est 0.
En conclusion, lorsque nous avons une forme indéterminée, il est souvent possible de factoriser pour simplifier l'expression et trouver la limite rapidement. Il est essentiel de s'entraîner sur ce type de méthodes pour bien les maîtriser.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Determiner une asymptote + étude
Dans ce cours, nous apprenons comment trouver les asymptotes d'une fonction. Les asymptotes peuvent être situées à moins l'infini, à plus l'infini, à la fois à moins l'infini et à plus l'infini, ou sur les bords de l'ensemble de définition de la fonction, là où il y a des valeurs interdites. Dans l'exemple donné, la fonction f(x) = -2/(1-x) est définie sur R privé de 1. Nous examinons les cas de moins l'infini et plus l'infini. Quand x tend vers moins l'infini, 1-x tend vers plus l'infini, et quand x tend vers plus l'infini, 1-x tend vers moins l'infini. Par quotient, nous concluons que f(x) tend vers moins l'infini en 0 et vers plus l'infini en 0. Nous en déduisons alors que la courbe CF a pour asymptote horizontale la droite d'équation y = 0, à moins et plus l'infini. Ensuite, nous examinons ce qui se passe en 1. Quand x tend vers 1 par valeur inférieure, 1-x tend vers 0 plus, et quand x tend vers 1 par valeur supérieure, 1-x tend vers 0 moins. Afin de confirmer cette tendance, nous pouvons choisir une valeur inférieure à 1, comme 0.1, où 1-0.1 est positif. Ainsi, 1-x tend vers plus l'infini en 1 par valeur inférieure. Nous pouvons également choisir une valeur supérieure à 1 pour vérifier. De ce fait, par quotient et en tenant compte du facteur -2, nous concluons que f(x) tend vers moins l'infini en 1 par valeur inférieure et vers plus l'infini en 1 par valeur supérieure. Lorsqu'il y a une valeur interdite, cela indique généralement une tendance vers plus ou moins l'infini, et nous avons alors une asymptote verticale. Ici, en x = 1, nous avons donc une asymptote verticale d'équation x = 1. En résumé, pour trouver les asymptotes, nous regardons les tendances en plus l'infini, moins l'infini et sur les bords de l'ensemble de définition de la fonction. Je recommande de vous entraîner à ces calculs et si vous avez des questions, consultez la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
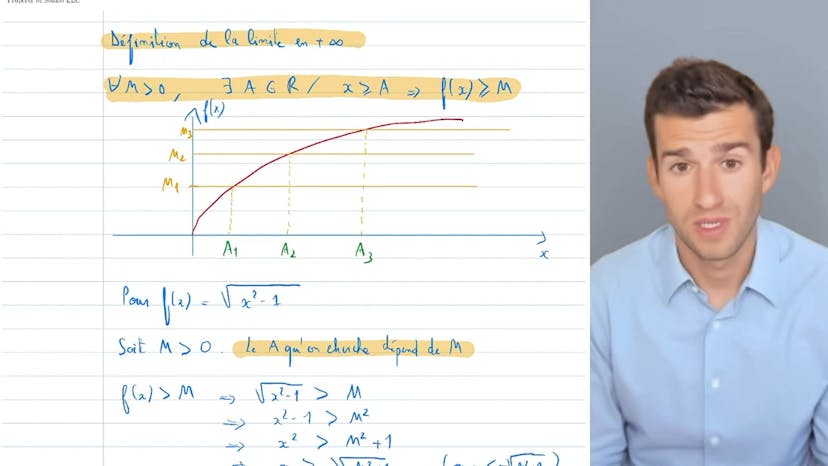
Calcul de limite infinie avec la définition (trouver un A)
La limite est définie comme étant lorsque une fonction tend vers l'infini. Peu importe la hauteur fixée, il y aura toujours un moment où la fonction la dépassera et sera au-dessus. Pour montrer cela, nous pouvons tracer des graphiques et fixer des valeurs pour m. A partir de ces valeurs, nous pouvons trouver les points où la fonction est toujours au-dessus de la hauteur fixée.
Dans cet exemple, nous avons tracé une fonction racine de x et fixé différentes valeurs pour m. Nous pouvons constater que peu importe la valeur de m, il existe toujours un réel a où la fonction est au-dessus de la hauteur fixée.
Ensuite, nous passons à un autre exemple où f(x) est égale à la racine de x carré moins 1. Pour montrer que la limite de cette fonction tend vers l'infini, nous devons trouver la valeur de a en résolvant l'inéquation f(x) > m. Nous trouvons a = racine de m carré plus 1. En utilisant cette valeur de a, nous pouvons montrer que si x est supérieur à a, alors f(x) sera supérieur à m.
Il est important de s'exercer avec différentes fonctions pour pratiquer cette méthode et trouver les bonnes valeurs de a. En fin de compte, il s'agit simplement de résoudre des équations. C'est ainsi que nous revenons à la définition formelle de la limite.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
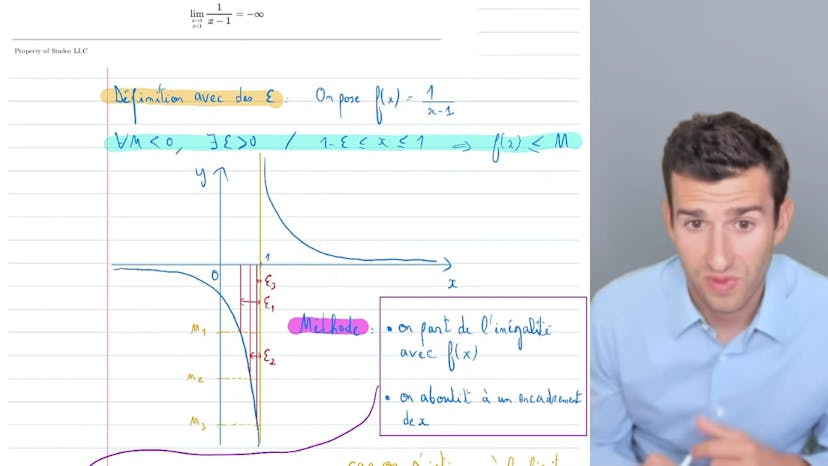
Calcul de limite finie avec la définition (trouver un epsilon)
La méthode que nous allons utiliser pour le calcul de la limite finie consiste à utiliser la définition formelle de la limite avec les epsilon. En utilisant cette méthode, nous pouvons montrer que la fonction tend vers moins l'infini.
Nous fixons un réel et nous choisissons une limite aussi basse que nous le souhaitons. Nous cherchons ensuite une valeur négative pour laquelle la fonction sera inférieure à cette limite. Nous trouvons un intervalle du type 1-epsilon1, où la fonction est inférieure à M1. Nous pouvons faire la même chose avec d'autres valeurs de M pour obtenir d'autres intervalles.
La méthode consiste à partir de l'inégalité f(x) inférieure à M, à résoudre f(x)-M et à trouver un encadrement de x qui nous permet de trouver l'epsilon correspondant. Nous prenons un réel M négatif, nous regardons la limite en 1- et nous résolvons f(x)-M, ce qui nous donne l'encadrement de x. Nous trouvons ensuite l'epsilon en utilisant cet encadrement.
En résumé, nous utilisons la méthode de l'encadrement pour trouver l'epsilon correspondant en partant de l'inégalité f(x) inférieure à M. Nous trouvons ainsi rigoureusement que la limite quand x tend vers 1- est moins l'infini. Il est important de s'exercer avec d'autres exemples pour bien comprendre cette méthode.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
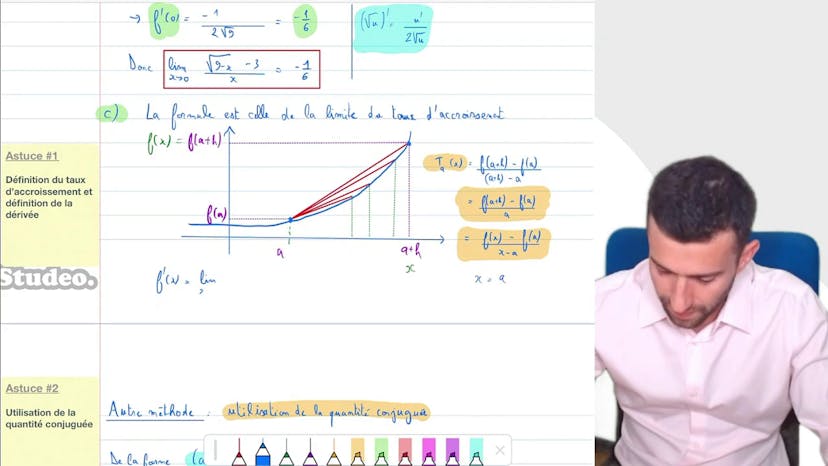
Utilisation de la dérivée
Dans cet exercice, nous devons trouver la limite d'une fonction en utilisant la dérivée. L'énoncé contient plusieurs exemples de ce type de problème. La première étape consiste à repérer les limites à calculer. Ensuite, nous utilisons la définition du taux d'accroissement pour réécrire la limite en utilisant la dérivée de la fonction. Ensuite, nous calculons la dérivée de la fonction et évaluons la dérivée en un point donné. Enfin, nous obtenons la limite en utilisant la dérivée calculée. Dans certains cas, il est possible d'utiliser une autre technique, comme la multiplication par la quantité conjuguée, pour lever l'indétermination de la limite. Il est important de vérifier si la limite est indéterminée au préalable. En utilisant ces méthodes, nous pouvons trouver les limites des fonctions données. Si des questions subsistent, il est possible de poser des commentaires dans la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
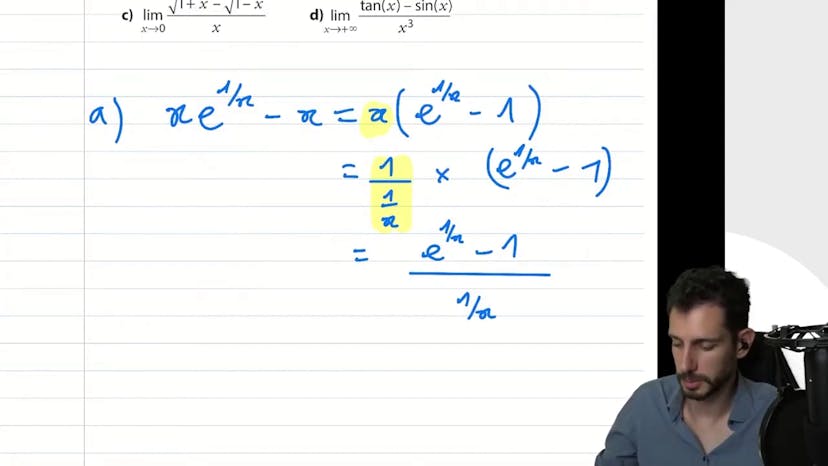
Encore un taux d'accroissement de exp
Ce cours porte sur le calcul de limites, avec un exemple particulièrement difficile : la limite de la fonction x exposant 1 sur x, moins x. Lorsque x tend vers l'infini, la fonction tend vers 1. Pour simplifier l'expression, on factorise par x, ce qui donne e de 1 sur x, moins 1. Cependant, cette simplification ne permet pas de résoudre l'indétermination de la forme. On utilise donc une astuce en posant x égal à 1 sur 1 sur x, ce qui donne e de quelque chose tendant vers 0, moins 1 sur quelque chose tendant vers 0. Cette limite est déjà connue et égale à 1. Ainsi, la limite de la fonction initiale est également égale à 1. Ce type d'exercice demande de repérer les formules et connaissances mathématiques spécifiques, afin de les appliquer de manière astucieuse pour obtenir la solution.
Révisions Maths lycée
Analyse Terminale
BCPST

Introduction Limites
L'étude des limites de fonction est plus complexe que celle des limites de suite. Une suite est une fonction qui porte uniquement sur les entiers, tandis qu'une fonction peut porter sur l'ensemble des réels. Il existe différents types de cas pour les limites de fonction, tels que les limites en l'infini et les limites en un réel. Certaines fonctions peuvent osciller à l'infini et n'ont pas de limite. Les limites peuvent converger vers une valeur réelle, diverger vers l'infini ou s'approcher d'une valeur réelle en s'éloignant de l'infini. Des exemples de graphes sont donnés pour illustrer ces différents cas. Dans ce chapitre, on étudiera ces différents cas en détail, avec des définitions et des exemples. On introduira également la notion d'asymptote. Les méthodes d'analyse graphique et de calcul de limites seront également abordées. Il faudra comprendre les définitions, connaître les exemples usuels et savoir utiliser les méthodes pour trouver une limite.
Révisions Maths lycée
Analyse Terminale
BCPST

En l'infini, limites finies et infinies
La première limite à connaître concerne une fonction qui tend vers l'infini lorsque x devient de plus en plus grand. Pour qu'une fonction tende vers l'infini, quel que soit le plateau y = A que l'on choisit, la fonction finit toujours par dépasser ce plateau. Cela signifie que pour un plateau donné, il existe une valeur de x à partir de laquelle toutes les valeurs de la fonction sont supérieures à ce plateau.
La deuxième limite concerne une fonction qui tend vers un réel L. Pour qu'une fonction ait une limite L, toutes les valeurs de la fonction finissent par être comprises dans un couloir autour de cette limite, quelle que soit la largeur du couloir.
Il est important de préciser que lorsque x tend vers plus l'infini, il faut toujours préciser cette condition. Enfin, la définition de la limite pour une fonction qui tend vers l'infini est similaire à celle des suites. Il faut toujours prendre en compte les couloirs autour de la limite et les plateaux pour comprendre ces concepts. Il est important de bien comprendre ces définitions pour les appliquer correctement dans les exercices.
Révisions Maths lycée
Analyse Terminale
BCPST

Les asymptotes horizontales
Dans ce cours, nous allons parler des limites de fonction lorsque X tend vers l'infini et de ce qu'est une asymptote. Une asymptote est une droite vers laquelle la courbe d'une fonction F se rapproche. Cela se produit lorsque la limite de F, lorsque X devient extrêmement grand, converge vers un réel appelé L. Il est important de noter que l'asymptote est à la courbe de F et non à F elle-même. Par exemple, si nous prenons la fonction 1/X, nous pouvons voir que la droite Y=3 est une asymptote à la courbe de F lorsque F s'approche de cette droite. De plus, une asymptote peut se rapprocher de manière croissante ou décroissante. Un autre exemple est le sinus, qui s'approche d'une droite asymptote lorsque nous changeons l'échelle. L'asymptote est donc la droite vers laquelle la courbe de F se rapproche infiniment. C'est tout ce qu'il y a à dire sur la notion d'asymptote horizontale.
Révisions Maths lycée
Analyse Terminale
BCPST

Bonus : Les asymptotes obliques
Dans cette vidéo, nous abordons le concept d'asymptote oblique. Habituellement, une asymptote est horizontale, mais dans ce cas particulier, elle possède une certaine pente. Pour une fonction f définie sur un ensemble de définition noté df, la courbe cf représente cette fonction. Une droite ax + b, appelée droite d, est une asymptote oblique de cf lorsque la différence entre f(2x) et ax + b tend vers 0 lorsque x tend vers l'infini. Dans ce cas, f(2x) tend vers l'infini, car elle suit une droite affine. Cela se produit fréquemment dans les exercices et il est important de savoir le détecter et le comprendre. Un exemple illustre cette situation, où une fonction verte se rapproche de plus en plus d'une droite rouge à mesure que x tend vers l'infini. Ce phénomène est visible même en zoomant sur une petite portion de la courbe. Dans cette vidéo, nous nous sommes concentrés sur les asymptotes obliques, mais les asymptotes verticales seront abordées dans une prochaine vidéo. N'hésitez pas à poser des questions ou à partager vos observations dans la FAQ. À bientôt pour la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

En un point réel, limite infinie
Le cours traite des limites de fonction lorsque x tend vers un réel A. Il explique qu'il y a deux cas principaux : une fonction qui tend vers plus ou moins l'infini, et une fonction qui converge vers une valeur finie. Le cas de convergence est plus simple, mais peut être étrange. La continuité est introduite comme une notion à voir ultérieurement. Des exemples simples et plus complexes sont donnés pour illustrer ces cas.
Ensuite, la limite infinie est abordée, en utilisant la notion de plateau de données. On définit la limite vers plus l'infini comme le fait que la fonction est indépassable par un plateau de données. Des exemples graphiques sont donnés pour illustrer cette notion. On introduit également la notion d'asymptote verticale, qui correspond à une limite infinie en un point fini. Un récapitulatif des différentes limites est ensuite présenté.
Le cours se termine en invitant les élèves à poser des questions, demander plus de détails et discuter dans la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Analyse graphique
Bonjour à tous ! Dans ce cours, nous allons aborder la limite des fonctions en effectuant une analyse graphique. Pour cela, nous nous concentrons sur une fonction tracée et cherchons à déterminer ses limites.
En examinant le graphique, nous constatons que lorsque x tend vers l'infini, la fonction tend vers zéro. Nous en concluons donc que cela est bel et bien une limite. De plus, lorsque x tend vers zéro avec des valeurs positives, nous observons que la courbe s'élève vers l'infini.
À partir de ces constatations, nous pouvons déduire que la fonction semble avoir deux asymptotes : une verticale en x = 0 et une horizontale en plus ou moins l'infini.
Lorsqu'on nous demande de fournir les équations des asymptotes, nous pouvons indiquer que l'asymptote horizontale est représentée par y = 0 et l'asymptote verticale par x = 0. Il est important de noter que l'on dit qu'une droite est asymptote à une courbe, et non à sa fonction.
Il est également possible qu'une droite soit asymptote en deux points, comme c'est le cas ici avec l'infini positif et l'infini négatif.
Voilà pour ce résumé SEO-friendly du cours sur les limites des fonctions. N'hésitez pas à poser vos questions si vous en avez. Vous pouvez retrouver le cours complet sur notre site.
Révisions Maths lycée
Analyse Terminale
BCPST

Calcul limite en un point fini par factorisation
Dans ce cours, nous apprenons une méthode pour trouver la limite d'une fonction lorsque nous avons une forme indéterminée. Cette méthode consiste souvent à factoriser pour éliminer l'indétermination.
Dans le premier exemple, nous avons la fonction f(x) = (x² - 2x) / (x - 1). Nous remarquons que cela peut être simplifié en utilisant l'identité remarquable (x-1)² / (x-1), ce qui donne simplement x-1. Ainsi, la limite de cette fonction tend vers 0, que ce soit de gauche ou de droite.
Dans le deuxième exemple, nous avons la fonction g(x) = (x² - 2x + 1) / (2x - 2). Nous avons ici un polynôme en bas, mais il peut être simplifié en le factorisant par 2. En utilisant la méthode classique pour trouver les racines du polynôme, nous obtenons les racines x1 = 1 et x2 = 2. Donc, nous pouvons factoriser g(x) en 2(x-1)(x-2). Cependant, il faut se rappeler de prendre en compte le coefficient dominant, qui est 2. Donc la fonction simplifiée devient (x-1) / (2x-2). Pour trouver la limite, nous devons déterminer les limites de chaque terme à gauche et à droite de 1. La limite de (x-1) est 1 de chaque côté. Le terme (2x-2) tend vers 0 à gauche de 1 et vers 2 à droite de 1. Ainsi, la limite de g(x) tend vers 1/2 à gauche de 1 et vers 1 à droite de 1.
En résumé, la méthode consiste à factoriser pour simplifier les expressions et éliminer les formes indéterminées. Ensuite, il faut déterminer les limites de chaque terme à gauche et à droite du point donné pour trouver la limite de la fonction. Il est également possible de tester les racines évidentes pour faciliter les calculs. N'oubliez pas de détailler si la limite tend vers 0 plus ou 0 moins lorsque vous effectuez des opérations supplémentaires avec la fraction dans des situations où cela est nécessaire.
Révisions Maths lycée
Analyse Terminale
BCPST

Determiner une asymptote + étude
Dans ce cours, nous apprenons comment trouver les asymptotes d'une fonction. Les asymptotes peuvent être trouvées soit en moins l'infini, soit en plus l'infini, soit les deux, soit sur les bords de l'ensemble de définition de la fonction. Pour trouver ces asymptotes, nous examinons les limites de la fonction aux extrémités de l'ensemble de définition. Dans cet exemple, nous avons la fonction f(x) = -2/(1-x), définie sur R (l'ensemble des réels) excluant 1. Nous examinons les limites de cette fonction en moins l'infini et en plus l'infini, qui tendent tous deux vers l'infini négatif. Nous pouvons donc conclure que la courbe CF a une asymptote horizontale, dont l'équation est y = 0, lorsque x tend en moins ou en plus l'infini. Ensuite, nous examinons la limite de la fonction en 1, par valeurs inférieures (x tend vers 1-) et par valeurs supérieures (x tend vers 1+), qui tendent toutes deux vers 0. Cela nous indique qu'il y a une asymptote verticale d'équation x = 1 en x égal à 1. En résumé, pour trouver les asymptotes, nous examinons les limites en plus l'infini, en moins l'infini et aux bords de l'ensemble de définition de la fonction. Pratiquez cet exercice et si vous avez des questions, consultez la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Calcul de limite infinie avec la définition (trouver un A)
Dans ce cours, nous abordons la définition formelle de la limite, qui peut être difficile à comprendre pour certains. Une limite signifie que ma fonction tend vers l'infini lorsque x devient infini. Peu importe la hauteur à laquelle je me fixe, il y aura toujours un moment où ma fonction dépassera cette hauteur. Pour illustrer cela, nous avons tracé une fonction racine carrée de x. Peu importe la hauteur m que je choisis, il y aura un réel a à partir duquel ma fonction sera toujours au-dessus de cette hauteur.
Dans l'exemple donné, nous prenons f(x) égal à la racine carrée de x au carré moins 1. Une fois que nous comprenons cette définition, il s'agit simplement de montrer l'existence d'un a qui dépendra de m en résolvant l'inéquation f(x) > m. Dans notre cas, cela devient x carré > m + 1. En regardant la limite à l'infini, nous prenons la solution positive, mais n'oublions pas qu'il y a aussi une solution négative. Ainsi, nous trouvons que x doit être supérieur à racine carrée de m carré + 1.
En utilisant l'implication inverse, nous montrons que si x est supérieur à ce a spécifique, alors f(x) sera supérieur à m. Nous avons donc utilisé la définition formelle de la limite pour montrer que la fonction tend vers l'infini lorsque x tend vers l'infini. Il est important de s'exercer avec différentes fonctions pour trouver la valeur de a qui convient. En fin de compte, il s'agit simplement de résoudre une équation.
Révisions Maths lycée
Analyse Terminale
BCPST

Calcul de limite finie avec la définition (trouver un epsilon)
Dans ce cours, nous examinons la définition formelle de la limite en utilisant des epsilon. L'idée est de montrer que pour n'importe quel niveau de limite fixé, il existe un intervalle dans lequel la fonction sera inférieure à une certaine valeur M. Pour cela, nous utilisons l'exemple de la fonction 1/(x-1) et fixons différentes valeurs de M.
En utilisant une méthode similaire, nous résolvons l'inégalité f(x) < M et obtenons un encadrement de x qui nous permet de trouver la valeur d'epsilon appropriée. Ensuite, nous montrons que pour tout x appartenant à l'intervalle 1-epsilon à 1, la fonction f(x) est inférieure à M, ce qui confirme notre objectif. En utilisant les définitions et les valeurs d'epsilon, nous démontrons rigoureusement que la limite de 1/(x-1) lorsque x tend vers 1- est égale à moins l'infini.
Il est recommandé de pratiquer davantage d'exercices similaires pour mieux comprendre cette méthode. En résumé, nous partons de l'inégalité f(x) < M et trouvons l'epsilon approprié en déroulant les calculs pas à pas. C'est ainsi que nous démontrons la limite en utilisant des définitions et des epsilon.
Révisions Maths lycée
Analyse Terminale
BCPST

Utilisation de la dérivée
Bonjour tout le monde ! Dans ce cours, nous allons corriger un exercice portant sur les limites utilisant le taux d'accroissement et la dérivée. Pour repérer les limites dans cet exercice, nous devons nous entraîner, car cela peut ne pas être évident au premier abord. Si vous avez des questions ou des difficultés, n'hésitez pas à les poser dans la FAQ. Le but de cet exercice est de nous familiariser avec les limites qui sont plus complexes lorsqu'elles font intervenir la dérivée. Nous allons commencer tout de suite avec la première limite. L'énoncé nous indique clairement qu'il faut utiliser la dérivée, donc nous savons que nous devons l'utiliser. "Dérivée" nous fait penser à "taux d'accroissement", donc nous allons réécrire la limite du taux d'accroissement. Nous allons revenir à la définition de la dérivée. Le taux d'accroissement, c'est quoi ? C'est quelque chose de la forme f(x+Δx) - f(x) / Δx. Quand Δx tend vers 0, cela converge vers f'(x), si la dérivée est bien définie. Une autre façon d'écrire cela est f(a+Δx) - f(a) / Δx, avec a égal à 0. Dans cet exercice, on nous demande de trouver f(x) = √(9-x), ce qui nous permet de trouver la dérivée. Maintenant, nous n'avons plus qu'à calculer la dérivée. En faisant le calcul, nous trouvons que f'(x) = -1/6. Donc nous en déduisons que la limite quand x tend vers 0 de √(9x) - 3 / x est égale à -1
Révisions Maths lycée
Analyse Terminale
BCPST
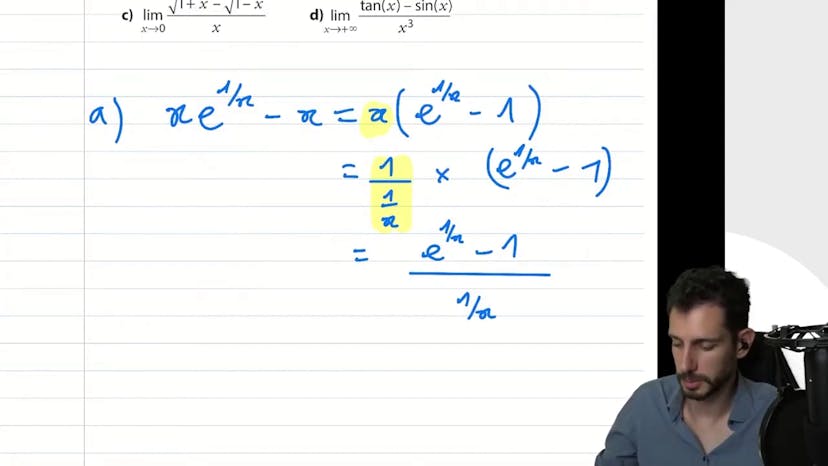
Encore un taux d'accroissement de exp
Le cours porte sur le calcul de limites en mathématiques. L'exemple étudié est la limite de la fonction f(x) = e^(1/x) - x lorsque x tend vers l'infini. Pour résoudre ce problème, l'élève utilise la factorisation par x pour simplifier l'expression. Cependant, il se retrouve avec une forme indéterminée. Il décide donc d'employer une autre méthode, celle du taux d'accroissement. En faisant une substitution astucieuse, il réécrit l'expression comme e^(1/(1/x)) - 1. Il remarque que le terme 1/x tend vers 0, ce qui lui permet de conclure que la limite de la fonction est 1. L'élève souligne que ce type d'exercice nécessite une bonne connaissance des formules mathématiques et la capacité de les utiliser dans des situations inhabituelles.
Révisions Maths lycée
Analyse Terminale
ECG

Introduction Limites
Lors de l'étude des limites de fonctions, nous pouvons nous inspirer de ce que nous avons fait avec les suites. Pour rappel, lorsque nous voyons les termes d'une suite se rapprocher d'une valeur et se coller à celle-ci, on dit que la suite converge. Les fonctions sont plus complexes que les suites car elles portent sur l'ensemble des réels, tandis que les suites se limitent aux entiers. Les fonctions peuvent donc prendre des valeurs pour tous les nombres réels, tels que -3, 0.74, racine de 2, etc. Il y aura donc plusieurs cas à étudier dans le cas des fonctions. En ce qui concerne les limites, nous pourrons parler de limites en l'infini (lorsque x tend vers l'infini), de limites en un réel (lorsque x tend vers un nombre réel spécifique), ainsi que des cas où il n'y a pas de limite. Il y aura également des cas où la fonction tendra vers une valeur réelle, vers plus l'infini, ou encore vers moins l'infini. Pour illustrer ces différents cas, des graphes peuvent être utilisés. Dans ce chapitre, nous verrons en détail tous ces exemples, avec des définitions et des exemples concrets. Nous aborderons également la notion d'asymptote, qui est une droite vers laquelle la fonction semble se coller. Nous étudierons tout cela à travers des exemples graphiques et des exercices. En résumé, il faudra connaître les définitions, les limites en plus ou moins l'infini, les exemples usuels, ainsi que les méthodes d'analyse graphique et de calcul de limites. N'hésitez pas à poser des questions ou à discuter avec les autres membres dans la FAQ.
Révisions Maths lycée
Analyse Terminale
ECG

En l'infini, limites finies et infinies
La limite d'une fonction lorsque x tend vers plus l'infini peut être définie de deux manières : soit la fonction tend vers l'infini (c'est-à-dire qu'elle dépasse n'importe quel plateau Y choisi), soit la fonction tend vers un réel L (c'est-à-dire que toutes les valeurs de la fonction finissent par être dans un couloir autour de L). Pour déterminer si une fonction tend vers l'infini, on peut choisir n'importe quel plateau Y et trouver une valeur de x à partir de laquelle toutes les valeurs de la fonction seront supérieures à ce plateau. Si cela est vrai pour tous les plateaux, alors la fonction diverge vers plus l'infini. Pour déterminer si une fonction tend vers un réel L, on trace un intervalle de taille quelconque autour de L et on recherche un moment où toutes les valeurs de la fonction sont comprises dans cet intervalle. Si cela est vrai pour tous les intervalles, alors L est une limite de la fonction. La notation pour exprimer cela est "limite de f(x) égale L lorsque x tend vers plus l'infini". Il est important de préciser que x tend vers plus l'infini dans cette notation. La limite d'une fonction est une propriété visuelle et peut être utilisée dans les exercices pour gagner des points facilement.
Révisions Maths lycée
Analyse Terminale
ECG

Les asymptotes horizontales
Dans cette transcription video, on aborde le sujet des asymptotes lorsque X tend vers l'infini. On se concentre principalement sur les asymptotes horizontales. Une asymptote horizontale est une droite vers laquelle la courbe de la fonction se rapproche lorsque la limite de la fonction F, lorsque X devient très grand, converge vers un réel appelé L. Il est important de mentionner que l'asymptote n'est pas la fonction F elle-même, mais la courbe de la fonction F. Il est également crucial de faire la distinction entre la droite et la fonction. Un exemple est donné pour illustrer le concept d'asymptote horizontale. Il est également mentionné que les fonctions peuvent se rapprocher de l'asymptote de manière croissante ou décroissante. Un autre exemple avec une fonction sinus est mentionné pour montrer qu'il n'est pas nécessaire que la fonction se colle à l'asymptote de manière croissante ou décroissante. En conclusion, une asymptote horizontale est une droite vers laquelle la courbe de la fonction se rapproche infiniment proche.
Révisions Maths lycée
Analyse Terminale
ECG

Bonus : Les asymptotes obliques
Lorsqu'il s'agit d'un cours en ligne, il est important de le rendre SEO-friendly, c'est-à-dire d'optimiser son contenu pour les moteurs de recherche. Voici un résumé SEO-friendly de ce cours sur les asymptotes obliques :
- Dans ce cours, nous nous intéressons aux asymptotes obliques, qui sont des cas particuliers où l'asymptote d'une fonction n'est plus horizontale mais inclinée.
- Une asymptote oblique est une droite représentée par l'équation y = ax + b, où a et b sont des réels.
- Lorsque la différence entre la valeur de la fonction f(x) et la droite ax + b tend vers 0 lorsque x tend vers l'infini, cela signifie que la courbe de la fonction se rapproche de plus en plus de la droite oblique.
- Cela se produit souvent dans les exercices mathématiques et il est essentiel de pouvoir le détecter et le comprendre.
- Un exemple illustrant ce concept est donné, où une courbe verte se rapproche d'une droite rouge lorsque l'on se déplace vers l'infini.
- Lorsque l'on zoom et que l'on regarde de plus près, la courbe verte semble être une droite, ce qui confirme l'existence d'une asymptote oblique.
- Ce concept d'asymptote oblique est souvent étudié en mathématiques et il est important de savoir l'identifier.
- Pour des questions supplémentaires ou des précisions, les apprenants sont invités à les poser dans la FAQ (Foire Aux Questions).
- La prochaine vidéo traitera des asymptotes verticales.
En résumé, ce cours explique le concept d'asymptote oblique et donne des exemples pour aider les apprenants à le comprendre. Il encourage également la participation des apprenants en posant des questions et partageant des informations dans la FAQ.
Révisions Maths lycée
Analyse Terminale
ECG

En un point réel, limite infinie
La limite de fonction avec X qui tend vers un réel A peut donner deux cas principaux : soit F part vers plus ou moins l'infini, soit F converge vers une valeur finie. Le premier cas est plus simple, mais il existe aussi des cas plus complexes comme la limite de sinus X sur X en 0, qui vaut 1. On peut visualiser ces limites sur un graphe. Ensuite, on introduit la notion de limite infinie en utilisant la notion de plateau. On peut approcher un point A par valeur supérieure ou inférieure, ce qui permet de définir les limites à gauche et à droite. Ensuite, on aborde la limite infinie en utilisant des exemples d'hyperboles. Quand la fonction ne peut être bloquée par un plateau, on dit qu'elle tend vers plus l'infini. Cela permet de définir des asymptotes verticales, représentées par des droites sur les graphes. En résumé, si la limite à gauche ou à droite de F2X quand X tend vers A est infinie, on appelle la droite X égale A une asymptote verticale.
Révisions Maths lycée
Analyse Terminale
ECG

Analyse graphique
Le cours porte sur l'analyse graphique des limites des fonctions. La première méthode d'introduction consiste à observer la courbe tracée et à déterminer les limites en utilisant cette analyse. Par exemple, on peut voir que lorsque x tend vers l'infini, la fonction tend vers 0. De même, lorsque x tend vers 0 par une valeur positive, la courbe s'éloigne vers l'infini. À partir de ces observations, on peut conclure que la fonction admet deux asymptotes : une verticale en x=0 et une horizontale en y=0. Pour écrire les équations de ces asymptotes, on utilise la forme y=a pour une droite horizontale et x=a pour une droite verticale. Il est également important de noter que l'on dit qu'une droite est asymptote à une courbe, et non à sa fonction. Enfin, il est possible qu'une droite soit asymptote en deux endroits, comme c'est le cas ici avec les asymptotes en plus et moins l'infini. Cette méthode d'introduction peut être utilisée pour déterminer les limites des fonctions en utilisant l'analyse graphique.
Révisions Maths lycée
Analyse Terminale
ECG

Calcul limite en un point fini par factorisation
Dans ce cours, nous avons examiné une méthode pour trouver la limite d'une fonction réelle donnée qui présente une forme indéterminée. Souvent, dans de tels cas, il suffit de factoriser pour lever l'indétermination.
Nous avons étudié deux exemples pour illustrer cette méthode. Dans le premier exemple, nous avions la fonction x²-2x sur x-1. En utilisant l'identité remarquable (x-1)² = x-1, nous avons simplifié cette fonction à x-1. Ainsi, la limite de cette fonction tend vers 0, que ce soit de droite ou de gauche.
Le deuxième exemple était un peu plus complexe. Nous avions la fonction (x²-2x+1)/(2x-2). Pour simplifier les calculs, nous avons factorisé cette fonction par 2, ce qui nous a donné (x-1)²/(2x-2). En utilisant la méthode classique pour trouver les racines d'un polynôme, nous avons trouvé que les racines de ce polynôme étaient 1 et 2. En factorisant par x-1, nous avons obtenu l'expression 2(x-1)(x-2)/(2x-2). En simplifiant davantage, nous avons obtenu (x-1)/(2x-2).
Ensuite, nous avons déterminé les limites à droite et à gauche de ces deux fonctions en x=1. Pour x-1, les limites étaient toutes les deux égales à 1. En ce qui concerne (x-1)/(2x-2), nous avons constaté que lorsque x tend vers 1, cette fonction tend vers 0.
Pour résumer, la méthode consiste à factoriser les fonctions pour lever l'indétermination et trouver leurs limites. Cette méthode peut être utile pour simplifier les calculs et résoudre rapidement des formes indéterminées.
Révisions Maths lycée
Analyse Terminale
ECG

Determiner une asymptote + étude
Dans ce cours, nous allons apprendre comment trouver les asymptotes d'une fonction. Les asymptotes peuvent être situées à moins l'infini, à plus l'infini, aux deux à la fois, ou sur les bords de l'ensemble de définition de la fonction lorsque des valeurs sont interdites. Nous allons examiner un exemple spécifique : f(x) = -2/(1-x), dont le domaine de définition est R privé de 1. Nous allons d'abord regarder les limites à moins l'infini et à plus l'infini de 1-x, qui tendent respectivement vers plus l'infini et moins l'infini. Par quotient, on peut en déduire que f(x) tend vers moins l'infini à moins l'infini et vers plus l'infini à plus l'infini. Cela signifie que la courbe CF a une asymptote horizontale correspondant à y=0 pour les valeurs de x allant vers plus et moins l'infini. Ensuite, nous examinons ce qui se passe en x=1. Pour 1-x, la limite par valeur inférieure tend vers 0+ et la limite par valeur supérieure tend vers 0-. En prenant des valeurs de x inférieures et supérieures à 1, on peut confirmer que c'est bien le cas. En appliquant le quotient avec le coefficient -2, nous trouvons que f(x) tend vers moins l'infini en 1- et vers plus l'infini en 1+. Lorsqu'il y a une valeur interdite, généralement, cela signifie que la fonction se rapproche de plus ou moins l'infini, et nous avons une asymptote verticale. Ainsi, en x=1, nous avons une asymptote verticale correspondant à x=1. En résumé, pour trouver les asymptotes, nous regardons les limites à plus l'infini, à moins l'infini et sur les bords de l'ensemble de définition de la fonction. Je vous encourage à vous entraîner sur cet aspect et si vous avez des questions, consultez la FAQ.
Révisions Maths lycée
Analyse Terminale
ECG

Calcul de limite infinie avec la définition (trouver un A)
Dans ce cours, nous abordons la notion de limite, qui peut être déroutante pour les étudiants. Une limite signifie essentiellement qu'une fonction tend vers l'infini lorsque son argument devient également infini. Cela signifie que quelle que soit la valeur que nous fixons comme objectif, la fonction la dépassera à un moment donné et restera toujours au-dessus de cette valeur. L'idée est donc de trouver un réel a à partir duquel, si x dépasse cette valeur, la fonction f(x) restera toujours supérieure à notre objectif.
Dans notre exemple, nous prenons une fonction de type racine carrée de x. Nous fixons différentes valeurs pour notre objectif, représentées par m. Pour chaque valeur de m, nous trouvons un réel a à partir duquel f(x) restera toujours au-dessus de notre objectif.
Ensuite, nous reprenons notre exemple avec une fonction f(x) égale à la racine carrée de x² moins 1. Une fois que nous avons compris la définition formelle de la limite, nous devons montrer l'existence de a en résolvant l'inéquation f(x) > m. En résolvant cette équation, nous trouvons que x² > m + 1. Comme nous regardons la limite à l'infini, nous prenons la solution positive et trouvons que x doit être supérieur à la racine carrée de m² + 1. Ainsi, nous avons trouvé notre valeur a.
En utilisant cette valeur a, nous remontons dans notre équation et montrons que f(x) est supérieure à m lorsque x est supérieur à a. Nous utilisons ainsi la définition formelle de la limite pour montrer que la fonction tend vers l'infini lorsque x tend vers l'infini.
Il est important de s'entraîner avec différentes fonctions pour maîtriser cette méthode de résolution d'équations et de retrouver la valeur a appropriée. En fin de compte, cela revient à résoudre des équations.
Révisions Maths lycée
Analyse Terminale
ECG

Calcul de limite finie avec la définition (trouver un epsilon)
Le cours porte sur le calcul de la limite finie en utilisant la définition formelle de la limite avec les epsilon. L'idée est de montrer que pour une limite donnée, il existe un intervalle où la fonction est inférieure à une certaine valeur M. Pour cela, on utilise l'inégalité f(x) < M et on résout pour obtenir un encadrement de x. En utilisant cette méthode, on peut démontrer rigoureusement que la limite lorsque x tend vers 1- est moins l'infini. Il est nécessaire de s'exercer régulièrement pour maîtriser cette méthode. Pour récapituler, il faut partir de l'inégalité f(x) < M et trouver l'épisylone qui convient en déroulant étape par étape.
Révisions Maths lycée
Analyse Terminale
ECG

Utilisation de la dérivée
Bonjour tout le monde, aujourd'hui nous allons corriger un exercice sur les limites utilisant le taux d'accroissement et la dérivée. Il y en a plusieurs dans l'exercice, il n'est pas toujours facile de les repérer immédiatement, il est donc important de s'entraîner régulièrement. Si vous avez des questions ou des incompréhensions, n'hésitez pas à les poser dans la FAQ. L'objectif est de se familiariser avec les limites qui sont un peu plus complexes en utilisant la dérivée. Commençons tout de suite par le premier exercice. L'énoncé est clair, il faut utiliser la dérivée, donc nous savons que nous devons l'utiliser. Je vois cela, je me dis "dérivée", donc avec des limites, je vais réécrire la limite du taux d'accroissement. Je reviens à la définition de la dérivée. Pour rappel, le taux d'accroissement est de la forme f(x+0) - f(0) / x, et lorsque x tend vers 0, cela tend vers f'(0), si la dérivée est bien définie. Une autre façon d'écrire cela, de manière plus générale, est f(a+x) - f(a) / x, avec a égal à 0 dans ce cas. Donc ici, que voyons-nous ? Notre fonction est f(x) = racine de 9-x, c'est ce que l'énoncé nous demande de calculer. Donc je regarde f(x) - f(0) / x, cela correspond exactement à ce que l'énoncé veut que je calcule. Donc lorsque je prends la limite de cela lorsque x tend vers 0, cela devient la limite du taux d'accroissement, et donc cela tend vers la dériv
Révisions Maths lycée
Analyse Terminale
ECG
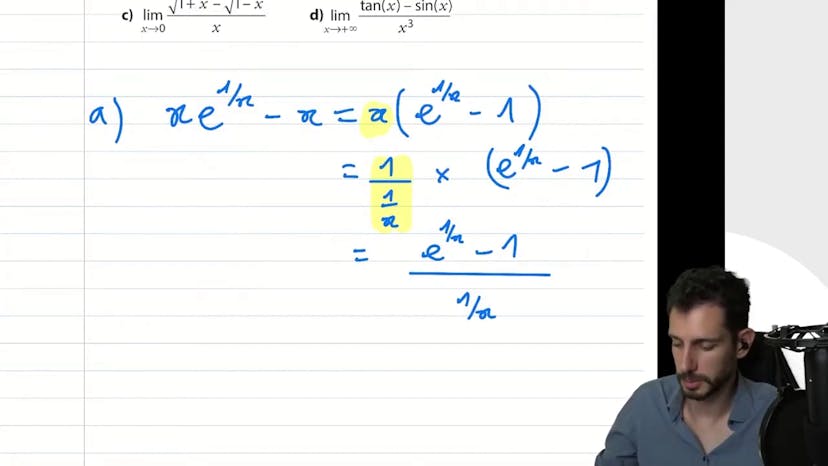
Encore un taux d'accroissement de exp
Dans cette vidéo, nous avons étudié le calcul de la limite de la fonction x exponentiel 1 sur x, moins x. Nous avons commencé par analyser le comportement de cette fonction lorsque x tend vers l'infini. Dans ce cas, la fonction tend vers 0. En factorisant par x, nous obtenons e de 1 sur x, moins 1. Cependant, cette forme ne permet pas de déterminer la limite car elle est toujours indéterminée. Nous avons donc utilisé une astuce en exprimant x comme 1 sur 1 sur x. Ainsi, la fonction devient e de petit machin qui tend vers 0, moins 1 sur le même machin qui tend vers 0. Cette limite est connue et vaut 1. Donc, la limite de la fonction étudiée est également 1. Ce type d'exercice est complexe car il nécessite de repérer les formules et connaissances mathématiques adéquates pour résoudre le problème.


