 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Déf formelle
La continuité en un point se définit comme suit : une fonction f est continue en un point a si et seulement si la limite finie de f(x) lorsque x s'approche de a est égale à f(a). Si cette condition est remplie pour tous les points d'un intervalle donné, on peut alors dire que la fonction est continue sur cet intervalle.
Une façon de comprendre cette notion de limite finie en un point est d'imaginer que l'on souhaite observer le comportement de la fonction lorsque x se rapproche de la valeur a. La fonction admet une limite l lorsque x tend vers a si, pour n'importe quel intervalle de taille donnée, il est possible de trouver un intervalle autour de a dans lequel les valeurs de la fonction sont toutes comprises dans l'intervalle initial.
En résumé, la continuité d'une fonction signifie que sa limite finie est égale à la valeur en ce point.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Discontinuités : exemples
La continuité d'une fonction est définie par le fait qu'il existe une limite finie en un point et que cette limite correspond à la valeur de la fonction en ce point. Pour illustrer cela, on peut utiliser un graphe de continuité.
Une discontinuité peut se présenter de différentes manières. Dans un premier exemple, il peut s'agir d'une discontinuité par non-existence ou non-définition du point. Par exemple, si on prend la fonction 1/x, le point zéro n'est même pas défini, donc la fonction n'est pas continue en ce point.
Dans un autre exemple, on peut avoir une discontinuité avec un saut. Par exemple, si on prend une fonction définie par une parabole à gauche et une parabole à droite qui ne sont pas connectées, il y a un saut au point de jonction. Dans ce cas, il est impossible de trouver un couloir vertical tel que toutes les valeurs de la fonction dans ce couloir soient dans le couloir orange.
Enfin, il peut y avoir une discontinuité avec un saut rattrapable. Par exemple, si on prend la fonction sinusX/X, elle n'est pas définie en zéro, mais on peut définir une valeur pour ce point qui permette de prolonger la fonction de manière continue. Il existe donc un point de continuité où la valeur de la fonction est 1 en zéro.
Ces différents exemples illustrent les différentes formes de discontinuité et montrent que certaines peuvent être rattrapables par une valeur appropriée au point de saut.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Fonctions usuelles
Ce cours porte sur la continuité des fonctions visuelles. Les fonctions x puissance n sont continues sur leur intervalle de définition. La fonction 1 sur x est continue sur son intervalle de définition, à l'exception de la valeur 0. La fonction racine carrée est continue sur l'intervalle de 0 à l'infini. La fonction valeur absolue est continue malgré un coin bizarre. Les fonctions exponentielle, sinus et cosinus sont également continues. Toutes les fonctions construites à partir de combinaisons de ces fonctions seront continues sur leurs intervalles de définition appropriés. Les fonctions non continues sont souvent celles qui sont construites par morceaux, comme les paraboles. Il existe différents types de discontinuités, notamment par définition, par sauts, prolongeables et mal placées. L'ensemble de définition d'une fonction n'est pas équivalent à son ensemble de continuité ou à son ensemble de dérivabilité. Par exemple, la fonction valeur absolue de x est définie sur R, continue sur R, mais non dérivable sur R. Elle est dérivable sur R étoile. N'hésitez pas à poser des questions dans le forum.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
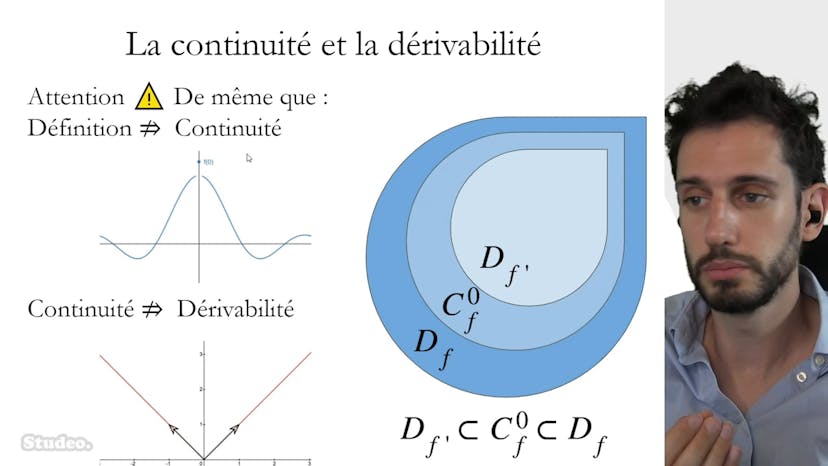
Continuité vs dérivabilité
Ce cours explique le lien entre dérivabilité et continuité. Il démontre que si une fonction est dérivable en un point, alors elle est continue en ce point. Cependant, le contraire n'est pas vrai. La démonstration utilise la définition de la dérivabilité d'une fonction f en un point A, qui donne la limite du taux d'accroissement de f quand x tend vers A. En utilisant cette expression, on peut isoler f de x et prendre la limite quand x tend vers A. Cela conduit à la conclusion que la limite de f de x quand x tend vers A égale f de A, ce qui est la définition de la continuité en ce point. Il est également souligné que la définiabilité n'implique pas la continuité, et la continuité n'implique pas la dérivabilité. Des exemples de fonctions non dérivables mais continues sont donnés, tels que la racine carrée en 0 et la valeur absolue. En résumé, l'ensemble des x où la fonction est dérivable est inclus dans l'ensemble des x où la fonction est continue, qui est lui-même inclus dans l'ensemble des x où la fonction est définie.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Continuité et suites : Théorème du point fixe
L'étude de la continuité dans le domaine des suites est très importante, et l'un des théorèmes fondamentaux est le théorème du point fixe. Ce théorème stipule que si une fonction f continue est définie sur un intervalle i, et qu'une suite un est définie de telle manière que pour tout n, un est dans i et un+1 est égal à f(un), alors si un converge vers l, où l est dans i, cela implique que f(l) = l. Ce résultat est intuitif car lorsque nous disons que la limite de f(x) lorsque x tend vers a est égale à f(a), cela nécessite la continuité de la fonction. Dans le théorème du point fixe, la suite un joue le rôle de x dans la définition de la continuité. Ainsi, si un tend vers l, alors la limite de f(un) est égale à f(l). Grâce à l'unicité de la limite, on peut conclure que l = f(l).
La démonstration du théorème du point fixe consiste à montrer que si un converge vers l, alors un+1 et f(l) convergent également vers l. En utilisant la continuité de f, on peut affirmer que la limite de f(x) lorsque x tend vers l est égale à f(l). En combinant ces résultats, on peut conclure que l = f(l).
En plus du théorème du point fixe, il est également important de mentionner que les comportements de convergence peuvent varier en fonction des propriétés de la fonction f et de la suite un. Par exemple, si f est une fonction continue mais croissante, et que la suite un est décroissante, la convergence peut prendre différentes formes, comme une approche en escalier ou en escargot vers le point d'intersection entre la fonction et la droite y = x.
En conclusion, l'étude de la continuité dans le domaine des suites est essentielle, et le théorème du point fixe est un résultat clé dans ce domaine. Il nous permet de comprendre comment les limites des termes d'une suite convergente sont liées à la fonction continue qui la génère.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
TVI : LE théorème
Le théorème des valeurs intermédiaires est un théorème capital en mathématiques, notamment pour les études de fonctions et la résolution d'équations. Il stipule que pour une fonction continue sur un intervalle donné, toute valeur comprise entre les images de deux points de l'intervalle aura au moins une solution correspondante dans cet intervalle. Ce théorème est illustré à l'aide d'un graphe montrant une courbe continue qui relie les points d'images correspondants des points de l'intervalle. En traçant une droite horizontale représentant une valeur k quelconque entre les images des points a et b, on constate qu'elle croise forcément la courbe, prouvant ainsi l'existence de solutions à l'équation f(x) = k. Ce résultat est valable même si la fonction ne fait que monter ou descendre de manière continue sans variation. Dans ce cas, il n'y aura qu'une seule solution à l'équation. Ce théorème permet de justifier l'existence de solutions dans différents cas et de les localiser. Il est important de l'appliquer en citant le théorème et en précisant si la fonction est continue ou strictement croissante/décroissante.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Continuité en un Point
Dans ce cours, nous examinons comment trouver la dérivée d'une fonction qui a plusieurs expressions sur différents intervalles. Nous constatons qu'elle peut ne pas être dérivable, bien qu'elle puisse être continue. Par exemple, pour la fonction f avec trois expressions selon les intervalles, nous vérifions si elle est parfaitement continue. La première condition pour qu'une fonction soit continue est qu'elle soit définie. Si elle n'est pas définie, il est inutile de poursuivre. Dans notre cas, elle est bien définie. Ensuite, excepté aux limites entre les intervalles, elle est continue sur les intervalles moins l'infini, 3, 3, 5 et 5 plus l'infini. Nous devons donc nous concentrer sur la continuité aux points 3 et 5 qui correspondent aux extrémités de ces intervalles. Comme nous avons deux expressions différentes à gauche et à droite de 3, nous devons vérifier la limite de x tendant vers 3 avec x inférieur à 3 et la limite de x tendant vers 3 avec x supérieur à 3. Ces limites doivent être égales et égales à f de 3 pour avoir la continuité. Dans notre cas, lorsque x tend vers 3 avec x inférieur à 3, nous utilisons la première expression, moins x plus 6. Lorsque x est supérieur à 3, nous utilisons également moins x plus 6. De plus, f de 3 vaut 3. Donc toutes les conditions requises pour que la fonction soit continue en 3 sont remplies. Ensuite, nous faisons la même chose pour 5. Nous examinons la limite lorsque x tend vers 5 avec x inférieur à 5 et la limite lorsque x tend vers 5 avec x supérieur à 5, et nous constatons que ce ne sont pas les mêmes expressions. Dans un cas, cela donne 7 et dans l'autre cas, cela donne 0, tandis que f de 5 vaut 0. Dès que la limite à droite n'est pas égale à la limite à gauche, la fonction ne peut pas être continue. Donc elle n'est pas continue en 5. Maintenant que nous avons examiné la continuité, les prochaines étapes consisteront à examiner la dérivabilité dans les méthodes suivantes.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Dérivabilité en un Point
Le cours porte sur la dérivabilité de la fonction valeur absolue. Il explique que la valeur absolue n'est pas dérivable en 0 car elle a une pente différente à gauche et à droite de ce point. Ensuite, il introduit une fonction qui comprend la valeur absolue, notée f(x) = |x|^2 + 2x - 3. Il explique que cette fonction est continue sur l'ensemble des réels car elle est composée d'un polynôme et de la fonction valeur absolue, qui sont toutes les deux continues. Cependant, en raison de la valeur absolue, la fonction présente une discontinuité de pente en -3 et en 1, ce qui la rend non dérivable en ces points. En observant graphiquement, on constate que la fonction n'est pas dérivable en -3 et 1, mais qu'elle est dérivable sur tous les autres points de l'ensemble des réels, à l'exception de ces deux points. Ce constat n'est pas une preuve formelle, mais simplement une observation. Cela conclut le premier aperçu des composés avec la fonction valeur absolue.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Prolongement par Continuité
Le prolongement par continuité est utilisé lorsque nous avons une fonction qui n'est pas définie en un point, mais dont la limite existe et est finie. Dans ce cas, nous pouvons prolonger la fonction en ce point en posant sa valeur égale à la limite de la fonction lorsque x tend vers ce point. Par exemple, si nous avons une fonction f(x) = x/x, qui n'est pas définie en 0, nous pouvons prolonger la fonction en posant f(0) = 1, ce qui rend la fonction définie et continue en ce point.
Dans l'exercice présenté, nous avons une fonction f(x) = x*sin(1/x), qui est définie pour toutes les valeurs de x sauf en 0 à cause du terme 1/x. Nous devons vérifier si cette fonction est bien un prolongement par continuité. En traçant la fonction sur une calculatrice, nous constatons qu'elle semble se rapprocher de 0 en 0. Pour le prouver, nous utilisons l'encadrement du sinus (qui est compris entre -1 et 1) en multipliant la fonction par la valeur absolue de x. En utilisant le théorème de l'encadrement, nous démontrons que la limite de la fonction est bien égale à 0. Ainsi, nous prouvons que la fonction f(x) = x*sin(1/x) est un prolongement par continuité avec f(0) = 0.
C'est donc une méthode utilisée pour prolonger une fonction définie sur un ensemble de valeurs à un point où elle n'est pas définie, en la rendant continue. Si vous avez d'autres questions, n'hésitez pas à les poser dans la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

TVI et Fonction Auxiliaire
Le cours aborde le théorème des valeurs intermédiaires, en utilisant une fonction compliquée comme exemple. La fonction étudiée est f(x) = (10x)/(e^x + 1). L'ensemble de définition est [0,+∞) car le dénominateur est toujours strictement positif. La fonction est définie et dérivable sur cet ensemble.
La dérivée de f(x) est obtenue en utilisant la formule du quotient de dérivées. On factorise ensuite cette expression pour obtenir une fonction g(x) = (1-x)e^x. On étudie les signes de g(x) pour appliquer le théorème des valeurs intermédiaires. On trouve que g(x) est strictement décroissante sur [0, +∞), passant de 2 à -∞. Donc, il existe un unique réel α tel que g(α) = 0.
Pour déterminer α de manière plus précise, on utilise une calculatrice pour encadrer sa valeur entre 1,28 et 1,29. Ensuite, on utilise les signes de g(x) pour déterminer les variations de f(x). On trouve que f(x) est croissante sur [0, α] et décroissante sur [α, +∞).
Les limites de f(x) sont calculées : f(0) = 0 et lim(x→+∞) f(x) = 0. Donc, la fonction f(x) est strictement croissante jusqu'à α où elle atteint un maximum, puis décroît progressivement vers une asymptote horizontale y = 0.
La stricte monotonie de la fonction est essentielle pour l'application du théorème des valeurs intermédiaires et l'unicité de l'antécédent. Un contre-exemple est donné pour illustrer ce point. La méthode complète est résumée avec les clés pour réussir ce type d'exercice. Si des questions subsistent, il est recommandé de consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Continuité et suites 1
Dans cette vidéo, nous étudions la méthode pour calculer la limite d'une suite définie par récurrence. Nous examinons les hypothèses nécessaires pour trouver et justifier correctement la limite. Nous utilisons la suite spécifique définie par u0 = 1 et un+1 = u*n – 1. Il est important de noter que la convergence peut dépendre du premier terme de la suite. Si une suite définie par récurrence du type un+1 = f(un) converge vers une limite L, alors un+1 converge également vers L. Pour trouver la limite, nous prenons la limite de l'égalité un+1 = f(un) en passant à la limite des termes. Nous obtenons l'équation f(L) = L, où L est un point fixe solution de cette équation. Cependant, cette méthode n'est valable que si la fonction f est continue. Il est essentiel de justifier la continuité dans cette méthode. Nous admettons dans l'énoncé que la suite converge vers L, et cela nous permet de supposer qu'elle a un point fixe, qui est l'unique limite possible. La représentation graphique de la suite en escalier converge vers 0, mais il est crucial de noter que la convergence dépend du premier terme u0. Si u0 est négatif, la suite divergera vers moins l'infini. Donc, u0 doit être positif pour que la suite converge. Il est également important de souligner que si la fonction f2x = x*e^2-x est discontinue, cette méthode ne fonctionne pas. Nous illustrons cela avec une fonction constante qui change brusquement en un point a. Dans ce cas, nous trouvons une suite spécifique qui converge vers a sans jamais atteindre a. Cette fonction n'est pas continue car la limite de f(un) est différente de f(L), où L est la limite de la suite. Ainsi, la continuité est essentielle dans cette méthode pour trouver et justifier correctement la limite.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Continuité et Suites 2
Ce cours traite de la méthode pour étudier la limite d'une suite définie par récurrence. Tout d'abord, la suite est associée à une fonction f telle que un+1 = f(un). La première étape est donc d'étudier la continuité de f, car elle sera nécessaire pour la suite du traitement. Ensuite, on résout l'équation f(x) = x pour trouver les éventuelles limites de la suite. Ensuite, on étudie la dérivabilité de la fonction f et sa croissance sur les intervalles où elle est définie. Il est important de noter que f peut ne pas être définie sur certains intervalles, ce qui peut impacter son comportement. Ensuite, on applique le principe de récurrence pour démontrer certaines propriétés de la suite, telles que son ordre de croissance et le fait qu'elle soit bornée. En utilisant ces propriétés, on peut conclure que la suite converge vers une limite L. Enfin, on utilise la continuité de f pour montrer que cette limite est également une solution de l'équation f(x) = x. La continuité de f est cruciale pour s'assurer que la limite recherchée appartient à l'ensemble des solutions de cette équation. En résumé, ce cours explique comment trouver la limite d'une suite définie par récurrence en étudiant la fonction associée, ses propriétés de continuité et de croissance, ainsi que l'application du principe de récurrence.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
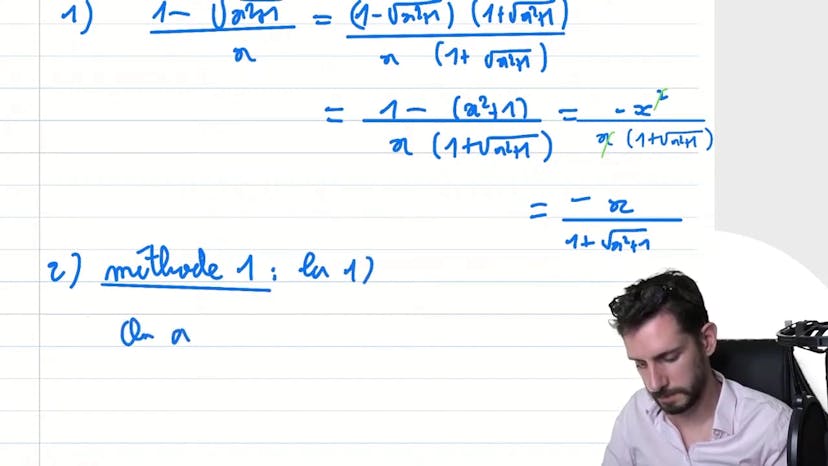
Saut de continuité
Le cours traite de la continuité d'une fonction définie par morceaux. On commence par introduire un exercice simple sur la continuité qui rappelle la définition de la continuité. Ensuite, on donne une fonction définie par f2x égale à une certaine valeur si x est différent de 0, et f2z égale à m si x vaut 0. On explique qu'il est possible d'écrire cette fonction sous une forme différente en utilisant la quantité conjuguée. On présente deux méthodes pour résoudre l'exercice. La méthode 1 consiste à utiliser la quantité conjuguée pour éliminer une forme indéterminée dans la limite de la fonction. La méthode 2 consiste à reconnaître un taux d'accroissement et à utiliser la dérivabilité de la fonction racine pour résoudre l'exercice. On conclut en disant que pour que la fonction f soit continue en 0, il faut que la valeur m soit égale à 0.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

TVI et expo
Dans cette leçon, nous étudions le nombre de solutions de l'équation E-x² = E2x-1. Graphiquement, nous avons représenté les deux fonctions E-x² et E2x-1. La première est une courbe en cloche symétrique par rapport à l'axe des ordonnées, tandis que la deuxième est une fonction exponentielle décalée de 1 vers le bas. En examinant le graphique, nous observons qu'il y a une solution autour de 0.552. De plus, pour les nombres négatifs, la fonction E-x² est toujours supérieure à la fonction E2x-1, tandis que pour les nombres positifs, il y a un point d'intersection où les deux fonctions se croisent.
Afin de démontrer mathématiquement ces observations, nous séparons l'étude en deux cas : R- (les nombres négatifs) et R+ (les nombres positifs). Pour les nombres négatifs, nous montrons que la fonction E-x² est strictement supérieure à la fonction E2x-1, en utilisant le fait que E2x-1 est négatif. Ainsi, il n'y a pas de solution à l'équation pour les nombres négatifs.
Ensuite, pour les nombres positifs, nous étudions la fonction f2x = E-x² - E2x-1. Nous montrons que cette fonction est strictement décroissante sur l'intervalle [0, +∞] en utilisant les propriétés des fonctions exponentielles. Nous montrons également que la limite de f2x quand x tend vers +∞ est -∞. En utilisant le théorème des valeurs intermédiaires, nous concluons qu'il existe une unique solution à l'équation pour les nombres positifs.
En résumé, il n'y a pas de solution à l'équation pour les nombres négatifs, et il y a une unique solution pour les nombres positifs.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

TVI et calculs costauds !
La fonction f(x) = 2/(e^x + e^(-x)) est étudiée.
Premièrement, on remarque que la fonction est toujours strictement positive car elle est une somme d'exponentielles positives. Ainsi, on peut exclure le cas où la fonction serait égale à 0.
Ensuite, on analyse graphiquement le nombre de solutions de l'équation f(x) = x. On trace la fonction et on observe qu'il y a une unique solution.
Pour montrer que la fonction g définie comme g(x) = f(x) - x est décroissante, on cherche d'abord si elle peut être décomposée en une somme de fonctions décroissantes. Cependant, on constate que f(x) n'est ni strictement croissante ni strictement décroissante, ce qui complique l'analyse.
On est donc obligé de passer par le calcul des dérivées. On dérive f(x) en utilisant une formule et en simplifiant, on obtient une expression à partir de laquelle on peut évaluer le signe de la dérivée.
Après une simplification et l'observation d'une identité remarquable, on arrive à exprimer g'(x) comme une somme de termes dont on peut déterminer les signes. On remarque que g'(x) est toujours négatif, ce qui montre que g(x) est décroissante.
En conclusion, on peut dresser un tableau de variation simplifié pour la fonction g : elle est décroissante, continue et admet un unique point d'intersection avec l'axe des abscisses.
Le nombre de solutions de l'équation f(x) = x est donc égal à 1.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Dérivabilité avec valeur absolue ?
Dans cet exercice, nous devons démontrer que la fonction donnée est continue et dérivable sur R, à l'exception du point x=0.
Tout d'abord, nous commençons par vérifier que la fonction est définie sur R. En effet, peu importe la valeur de x, 1+x est strictement différent de 0, ce qui nous permet d'avoir une définition valide de la fonction. De plus, nous savons que le quotient de deux fonctions continues donne une fonction continue.
Pour démontrer la continuité de la fonction, nous utilisons une calculatrice pour tracer son graphique et constatons qu'elle semble se rapprocher de 1 quand x tend vers l'infini et de -1 quand x tend vers moins l'infini. La fonction semble également relativement lisse, sans rupture de pente, ce qui soutient notre intuition de continuité.
En ce qui concerne la dérivabilité de la fonction, nous supposons qu'elle est dérivable en x=0, car elle est clairement dérivable pour tous les autres points de R. En effet, x est dérivable sur R et 1+x en valeur absolue est dérivable partout sauf en 0. S'appuyant sur cette hypothèse, nous concluons que la fonction est dérivable sur tout R, à l'exception de x=0.
Pour déterminer l'expression de la fonction en fonction du signe de x, cela est relativement simple. En vérifiant le comportement de la fonction en x=0, nous constatons qu'elle est bien continue, ce qui confirme notre expression.
Enfin, pour justifier que la fonction est dérivable partout, sauf en x=0, nous utilisons le fait que x est dérivable et que le quotient de deux fonctions dérivables donne une fonction dérivable. Nous effectuons les calculs nécessaires pour dériver la fonction en x=0 et vérifions que le résultat est cohérent de chaque côté de ce point. Nous constatons que les dérivées de chaque côté de x=0 sont égales à 1, confirmant ainsi la dérivabilité de la fonction.
En conclusion, nous démontrons que la fonction donnée est continue sur R et dérivable partout, sauf en x=0.
Révisions Maths lycée
Analyse Terminale
BCPST

Déf formelle
La continuité d'une fonction en un point est définie comme suit : une fonction est continue en un point a si et seulement si la limite de f(x) quand x approche de a est égale à f(a). Si cette condition est vérifiée pour tous les points d'un intervalle donné, on dira que la fonction est continue sur cet intervalle. Géométriquement, cela signifie que si on trace le graphique de la fonction, on peut le faire sans lever le stylo. Pour déterminer si une fonction admet une limite finie en un point, on sélectionne un intervalle autour de ce point et on vérifie si toutes les valeurs de la fonction dans cet intervalle sont comprises dans un autre intervalle plus grand. Si c'est le cas pour n'importe quelle taille d'intervalle, alors la fonction admet une limite finie en ce point. La continuité est donc définie comme le fait que la limite finie soit égale à f(a).
Révisions Maths lycée
Analyse Terminale
BCPST

Discontinuités : exemples
Une "discontinuité" se produit lorsque les valeurs d'une fonction ne se comportent pas de manière continue et prévisible. Une "continuité" se produit lorsque les valeurs d'une fonction se situent dans une certaine plage définie.
Dans ces exemples, on étudie différentes formes de discontinuités.
Le premier exemple montre une discontinuité due à l'inexistence d'un point. Par exemple, la fonction 1/x n'est même pas définie pour x=0. La fonction n'est donc pas continue en x=0 car elle n'est pas définie à cet endroit. La fonction a également des valeurs qui tendent vers l'infini à droite et à gauche de zéro.
Le deuxième exemple montre une discontinuité due à un saut. La fonction est définie comme une parabole décroissante à gauche et une parabole croissante à droite. Il y a un saut, car en x=0, il n'y a pas de valeur définie à gauche, mais la valeur 0 est attribuée à la branche de droite. Aucun couloir de taille quelconque ne contient toutes les valeurs de la fonction, car il y a des valeurs en dehors du couloir orange, qu'on prenne un couloir de grande taille ou de petite taille.
Le troisième exemple montre une discontinuité rattrapable. La fonction sin(x)/x n'est pas définie en x=0, car diviser par zéro est interdit. Cependant, un point supplémentaire peut être ajouté à la définition de la fonction en x=0 pour rendre la fonction continue. Dans ce cas, la valeur du point de continuité est 1.7, ce qui permet à la fonction de se prolonger de manière continue.
Ces exemples illustrent différentes formes de discontinuités et montrent comment une fonction peut ou ne peut pas être continue en différents points.
Révisions Maths lycée
Analyse Terminale
BCPST

Fonctions usuelles
Ce cours traite de la continuité des fonctions visuelles et récapitule les principales fonctions continues rencontrées depuis le lycée, telles que les fonctions linéaires, les fonctions puissances, la fonction inverse, la fonction racine carrée, la fonction valeur absolue, la fonction exponentielle, le sinus et le cosinus, ainsi que toutes les fonctions construites à partir de ces fonctions par des combinaisons, des compositions, des divisions, des multiplications, etc. Il est souligné que la plupart des fonctions discontinues sont construites par morceaux et par branches, comme les paraboles volontairement non continues. Ensuite, différents types de discontinuités sont expliqués, tels que les discontinuités par définition, les sauts de discontinuité, les discontinuités prolongeables et les discontinuités en un point mal placé non-prolongeables. Il est également précisé que l'ensemble de définition des fonctions n'est pas égal à leur ensemble de continuité ni à leur ensemble de dérivabilité. Par exemple, la fonction valeur absolue de x est définie sur R, continue sur R, mais non dérivable sur R, tandis qu'elle est dérivable sur R étoile. Le cours se termine en encourageant les étudiants à poser des questions sur le forum et en annonçant une prochaine vidéo. N'hésitez pas à poser des questions dans le forum encore une fois et je vous retrouve pour une prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

Continuité vs dérivabilité
Ce cours explique le lien entre dérivabilité et continuité d'une fonction. Il démontre que si une fonction est dérivable en un point, alors elle est continue en ce point, mais que le contraire n'est pas vrai. Pour démontrer cela, il utilise la définition de la dérivabilité et la limite du taux d'accroissement. Il montre également que la définition de continuité peut être représentée par la limite de la fonction. Il souligne que la dérivabilité n'implique pas la continuité, tout comme la continuité n'implique pas la dérivabilité. En conclusion, l'ensemble des points où la fonction est dérivable est plus petit que l'ensemble des points où elle est continue, qui est lui-même contenu dans l'ensemble des points où la fonction est définie. Deux exemples de fonctions continue mais non dérivable sont donnés : la racine carrée en 0 et la valeur absolue.
Révisions Maths lycée
Analyse Terminale
BCPST

Continuité et suites : Théorème du point fixe
Une application importante de l'étude de la continuité est l'étude des suites. Le théorème du point fixe est un théorème fondamental qui dit que si une suite converge vers une valeur l et qu'une fonction f continue sur un intervalle i, alors f(l) = l. Ce théorème repose sur la définition de la continuité, qui dit que pour que la limite de f(x) lorsque x tend vers a soit égale à f(a), il faut que f soit continue. La démonstration du théorème repose sur l'utilisation de la continuité de f et de la notion de limite. Ensuite, il est important de noter que les comportements de convergence des suites définies de manière récurrente peuvent varier en fonction de la nature de la fonction f: une fonction croissante de type concave peut donner une convergence en escalier, tandis qu'une fonction décroissante de type convexe peut donner une convergence en escargot. Ce rappel conclut la vidéo.
Révisions Maths lycée
Analyse Terminale
BCPST

TVI : LE théorème
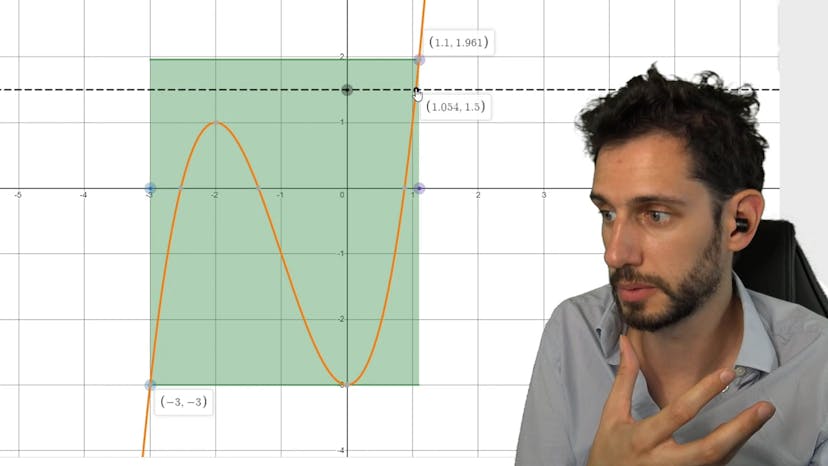
Le théorème des valeurs intermédiaires est un concept important en mathématiques, notamment en études de fonctions et résolution d'équations. Ce théorème stipule que pour une fonction continue f sur un intervalle [a, b], toute valeur k comprise entre f(a) et f(b) admet au moins une solution c dans l'intervalle [a, b].
Pour illustrer ce théorème, on peut visualiser graphiquement le comportement de la fonction f à l'aide d'un graphe. On trace la courbe représentant la fonction f(x), qui dans cet exemple est une courbe en forme de x3. On considère ensuite l'intervalle [a, b] défini par les points de la courbe. La fonction f(a) correspond à un point sur la courbe à l'extrémité gauche de l'intervalle, et f(b) correspond à un point à l'extrémité droite de l'intervalle.
En reliant les deux points avec une courbe continue, on montre que pour toute valeur k située entre f(a) et f(b), il y a nécessairement une intersection entre la courbe de la fonction et une droite horizontale tracée au niveau de k. En d'autres termes, l'équation f(x) = k admet au moins une solution dans l'intervalle [a, b].
Ce phénomène est dû à la continuité de la fonction f. En ne levant jamais le stylo lors du tracé de la courbe entre les points a et b, on garantit qu'il y aura toujours une intersection entre la courbe et la droite k, quelle que soit la valeur de k. Cette propriété s'applique également lorsque la fonction f est strictement croissante ou strictement décroissante, où il n'y aura qu'une seule intersection entre la courbe et la droite k.
Il est important de justifier l'utilisation du théorème des valeurs intermédiaires en citant le théorème lui-même et en précisant que la fonction est continue. De plus, ce théorème peut également être utilisé pour déterminer le nombre de solutions sur des intervalles spécifiques, en se basant sur la monotonicité de la fonction.
En résumé, le théorème des valeurs intermédiaires est un outil fondamental en mathématiques, permettant de garantir l'existence de solutions pour certaines équations lorsque l'on ne peut pas les trouver exactement. Il repose sur la continuité de la fonction et assure qu'il y aura toujours au moins une solution dans un intervalle donné.
Révisions Maths lycée
Analyse Terminale
BCPST

Continuité en un Point
Dans cette transcription vidéo, nous abordons la manière de trouver la dérivée d'une fonction qui présente différentes expressions sur différents intervalles. Nous constatons que cette fonction n'est pas nécessairement dérivable, bien qu'elle puisse être continue. Par exemple, pour la fonction f qui est définie par trois expressions selon trois intervalles, nous examinons sa continuité. Tout d'abord, pour qu'une fonction soit continue, il est essentiel qu'elle soit au moins définie. Si ce n'est pas le cas, il est inutile de poursuivre. Dans ce cas-ci, elle est bien définie, notamment grâce à la deuxième expression qui s'applique lorsque x est supérieur ou égal à 3. En dehors des limites entre les intervalles, f est bien continue de moins l'infini à 3, de 3 à 5, et de 5 à plus l'infini. Nous devons donc nous concentrer sur la continuité aux points 3 et 5, qui correspondent aux extrémités de ces intervalles. Étant donné qu'il y a deux expressions différentes à gauche et à droite de 3, nous examinons la limite de x approchant 3 avec x inférieur à 3 et la limite de x approchant 3 avec x supérieur à 3. Il est essentiel que ces limites soient égales et égales à f de 3 pour garantir la continuité. Lorsque x approche 3 avec x inférieur à 3, nous utilisons la première expression, soit moins x plus 6, ce qui donne 3 en approchant 3 par la gauche. Lorsque x est supérieur à 3, cela donne également 3. Par ailleurs, f de 3 équivaut à 3. Ainsi, toutes les conditions requises pour assurer la continuité de la fonction en 3 sont satisfaites. Nous avons f de 3 égal à 3, la limite de gauche et de droite de f est bien égale à f de 3. Ensuite, nous passons au deuxième point, qui est 5. Nous faisons exactement la même démarche. Nous examinons la limite de x approchant 5 avec x inférieur à 5, la limite de x approchant 5 avec x supérieur à 5, et nous constatons que les expressions ne sont pas les mêmes dans les deux cas. L'une donne 7, l'autre donne 0, et f de 5 lui-même vaut 0. En réalité, il n'était même pas nécessaire de vérifier cela. Dès lors que la limite de droite n'est pas égale à la limite de gauche, il est évident que la fonction ne peut pas être continue. Ainsi, la fonction n'est pas continue en 5. Voilà, nous avons abordé la continuité. Dans les prochaines étapes, nous examinerons également la dérivabilité, ce qui sera traité plus en détails dans les prochaines méthodes.
Révisions Maths lycée
Analyse Terminale
BCPST

Dérivabilité en un Point
Dans cette vidéo, nous examinons la dérivabilité de la fonction valeur absolue et son impact sur une nouvelle fonction, f(x) = |x|^2 + 2x - 3.
La fonction valeur absolue n'est pas dérivable en 0 car elle présente une discontinuité à cet endroit, avec des pentes différentes à gauche et à droite de zéro.
La fonction f(x) est continue sur l'ensemble des réels car elle est composée d'un polynôme et de la fonction valeur absolue, qui sont toutes deux continues. Bien que la valeur absolue ne soit pas dérivable, elle reste continue.
En traçant le graphique de f(x), on constate que la fonction présente une discontinuité de pente aux points -3 et 1, en raison de la valeur absolue. Cependant, sur tous les autres points, la fonction est dérivable.
Ainsi, d'après l'observation graphique, f(x) est dérivable sur l'ensemble des réels, à l'exception des points -3 et 1.
Ceci conclut notre aperçu des compositions avec la fonction valeur absolue.
Révisions Maths lycée
Analyse Terminale
BCPST

Prolongement par Continuité
Le prolongement par continuité est utilisé dans les cas où une fonction n'est pas définie en un point, mais la limite de la fonction existe et est finie. Dans ce cas, on peut prolonger la fonction en ce point en posant la valeur de la limite comme valeur de la fonction en ce point.
Un exemple de ce type de prolongement est la fonction f(x) = x/x. Cette fonction n'est pas définie en 0 à cause du dénominateur, mais on peut la prolonger par continuité en posant f(0) = 1. Ainsi, on obtient une fonction définie et continue en tout point.
Dans l'exercice présenté, on nous propose la fonction f(x) = x sin(1/x) pour x différent de 0, avec f(0) = 0. On veut vérifier si cette fonction est bien le prolongement par continuité de la fonction donnée. Pour cela, on observe le graphique de la fonction et on constate qu'elle semble se rapprocher de 0 en 0. On peut conjecturer que la fonction est continue en 0. Pour le prouver, on utilise une astuce en encadrant la fonction sin(1/x) entre -1 et 1. Ensuite, on multiplie par la valeur absolue de x pour obtenir une expression encadrée entre 0 et x. Quand x tend vers 0, cette expression tend vers 0, ce qui nous permet d'utiliser le théorème d'encadrement pour prouver que la limite de la fonction est bien 0. Ainsi, on démontre que la fonction f est continuellement 0, ce qui confirme que c'est bien un prolongement par continuité.
En conclusion, le prolongement par continuité est une technique utilisée pour étendre une fonction à un point où elle n'est pas définie, en posant la limite de la fonction comme valeur en ce point. Il est important de vérifier la continuité de la fonction prolongée en utilisant des méthodes telles que l'encadrement et le théorème d'encadrement.
Révisions Maths lycée
Analyse Terminale
BCPST

TVI et Fonction Auxiliaire
Le cours aborde le thème du théorème des valeurs intermédiaires en utilisant une fonction complexe. La fonction f(x) = 10x / (e^x + 1) est étudiée, en montrant d'abord que son ensemble de définition est i ici, c'est-à-dire 0 à l'infini. Ensuite, la dérivée de f est calculée, f'(x) = (1 - x) * e^x, en factorisant pour obtenir une fonction g(x) = 1 - x * e^x. L'objectif est de montrer qu'il existe un réel unique alpha tel que g(2alpha) = 0 en utilisant le théorème des valeurs intermédiaires. Pour cela, il est nécessaire d'établir la continuité de g et de montrer sa stricte décroissance. Une calculatrice est utilisée pour trouver une approximation de la valeur de alpha, qui est comprise entre 1,29 et 1,28. Ensuite, le signe de g est déterminé, ce qui permet de déterminer le sens de variation de f. Il est conclu que f est croissante sur 0 à alpha et décroissante à partir de alpha. Les limites de f sont calculées, f(0) = 0 et lim(x→+∞) f(x) = 0. Un graphique de f est tracé pour illustrer ces résultats. Enfin, l'importance de la stricte monotonie dans l'application du théorème des valeurs intermédiaires est soulignée à travers un exemple.
Révisions Maths lycée
Analyse Terminale
BCPST

Continuité et suites 1
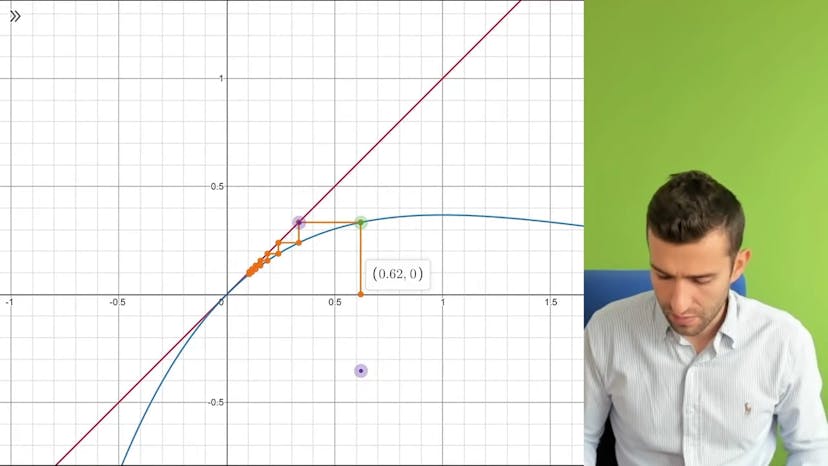
Dans ce cours, nous nous intéressons à la méthode de calcul de limite pour une suite définie par récurrence. Cette méthode est applicable aux suites dites "en escalier". Pour bien trouver et justifier la limite de ces suites, il est important de vérifier certaines hypothèses.
La méthode consiste à considérer une suite définie par une relation de la forme un+1 = f(un), où f est une fonction. Si la suite converge vers une limite L, alors un+1 converge également vers L. En prenant la limite de l'égalité un+1 = f(un), on obtient L = f(L). L est nécessairement un point fixe de l'équation f(x) = x. Il est important de noter que cette propriété est valable uniquement si f est une fonction continue.
En utilisant la continuité de f, on peut justifier que la suite converge vers L en montrant que L est le point fixe de f. Si f admet plusieurs points fixes, il faut étudier chaque cas individuellement pour déterminer la limite. Si f n'a pas de point fixe, alors la suite n'a pas de limite.
La vidéo donne un exemple concret de suite définie par récurrence, où u0 = 1 et un+1 = u*e^2 - u. On résout l'équation f(x) = x pour trouver les points fixes de cette suite. On trouve que le seul point fixe est x = 0. Comme il a été supposé que la suite converge, la limite de la suite est donc 0.
Il est souligné que le premier terme de la suite (u0) a une influence capitale sur sa convergence. Si u0 est positif, la suite converge vers 0, mais si u0 est négatif, la suite diverge vers -∞. Il est donc primordial de tenir compte du premier terme lors de l'étude de convergence des suites définies par récurrence.
Enfin, il est démontré l'importance de la continuité de la fonction f pour cette méthode. Un contre-exemple est donné avec une fonction discontinue, où une suite particulière converge vers un réel a sans jamais atteindre a. Il est expliqué que dans ce cas, la limite de f(un) diffère de f(a), ce qui contredit la propriété utilisée dans la méthode.
En conclusion, la méthode de calcul de limite pour une suite définie par récurrence en escalier nécessite de vérifier la continuité de la fonction f et prend en compte le premier terme de la suite. La limite de la suite est l'un des points fixes de l'équation f(x) = x. Si cette équation n'a pas de solution, la suite n'a pas de limite.
Révisions Maths lycée
Analyse Terminale
BCPST

Continuité et Suites 2
Ce cours porte sur l'étude des suites définies par récurrence et l'analyse de leur limite. Pour cela, on associe une fonction f à la suite et on étudie la continuité de cette fonction. En résolvant l'équation f(x) = x, on peut trouver les limites possibles de la suite. Ensuite, on étudie la dérivabilité de la fonction f et sa croissance. Il est important de noter que la continuité de f est essentielle dans cette étude. On utilise ensuite la méthode de récurrence pour démontrer certaines propriétés de la suite, notamment sa croissance et son caractère borné. On conclut que la suite converge vers une limite L, qui doit être solution de l'équation f(x) = x. La continuité de f est cruciale pour cette conclusion. Enfin, on précise que ce théorème ne s'applique que si f est continue. Un exemple est donné pour illustrer l'importance de la continuité de f.
Révisions Maths lycée
Analyse Terminale
BCPST
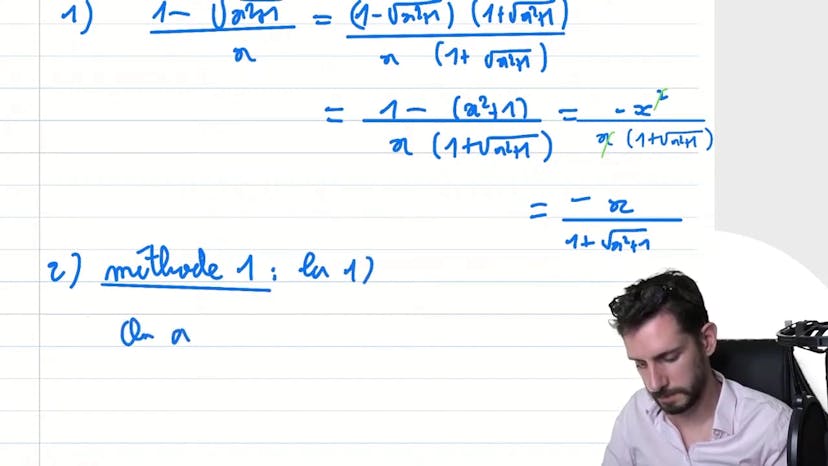
Saut de continuité
Ce cours porte sur la continuité des fonctions et propose quelques exercices pour mettre en pratique cette notion. Le premier exercice consiste à déterminer si une fonction est continue ou non. On nous donne une fonction définie par des morceaux et un point isolé. Pour résoudre cet exercice, deux méthodes sont proposées : la première utilise la quantité conjuguée pour simplifier l'expression, tandis que la deuxième exploite la dérivabilité de la fonction pour déterminer si elle est continue. La deuxième méthode est plus complexe mais permet de mieux comprendre le concept de continuité. Ensuite, la question b demande de trouver une valeur de m pour laquelle la fonction est continue en 0. La réponse est que m doit être égal à 0, selon la définition fondamentale de la continuité.
Révisions Maths lycée
Analyse Terminale
BCPST

TVI et expo
Dans ce cours, nous étudions graphiquement le nombre de solutions d'une équation. Nous avons deux fonctions, E-x² et E2x-1. La première est une courbe en cloche classique et la seconde est la fonction exponentielle décalée d'une unité vers le bas. Graphiquement, nous observons une solution approximative à x=0.552. Nous constatons que pour les nombres négatifs, la fonction E-x² est toujours au-dessus de la fonction E2x-1, tandis que pour les nombres positifs, les deux fonctions s'intersectent après un changement de comportement. En utilisant cette intuition graphique, nous pouvons rapidement répondre à certaines questions, telles que démontrer que pour tout nombre réel négatif, la fonction E-x² est supérieure à l'autre. Nous utilisons le fait que la fonction exponentielle est strictement croissante. Pour les nombres positifs, nous utilisons une méthode classique où nous posons une fonction égale à zéro et montrons qu'elle est strictement décroissante sur R+. Nous déduisons alors qu'il existe une solution unique à l'équation. En utilisant le théorème des valeurs intermédiaires, nous pouvons prouver qu'il n'y a pas de solution sur R- et qu'il y a une unique solution sur R+. En conclusion, l'équation a une unique solution sur R, ce qui correspond à l'intuition graphique initiale.
Révisions Maths lycée
Analyse Terminale
BCPST

TVI et calculs costauds !
La fonction f est définie sur R par f(x) = 2/(e^x + e^(-x)).
Avant de commencer, vérifions si f(x) peut valoir 0 à certains moments et poser des problèmes de définition. Comme f(x) est une somme d'exponentielles, et que les exponentielles sont strictement positives, f(x) ne peut jamais être égal à 0. Donc nous pouvons être confiants.
Réfléchissons graphiquement au nombre de solutions sur R de l'équation f(x) = x.
En traçant la fonction 2/(e^x + e^(-x)) = x, nous obtenons une seule solution, x = 2.
Passons maintenant à l'étape suivante. On pose la fonction g(x) = f(x) - x. Pour montrer que g est décroissante, on pourrait espérer que g soit la somme de fonctions décroissantes. Malheureusement, nous avons déjà vu graphiquement que f(x) n'est pas décroissante, mais plutôt croissante puis décroissante, donc ce n'est pas le cas. Nous devons donc calculer les dérivées.
Calculons d'abord la dérivée de f. La dérivée de 2/(e^x + e^(-x)) est 2*(-e^x + e^(-x))/(e^x + e^(-x))^2.
Maintenant, vérifions le signe de cette dérivée. Mettons tout au même dénominateur : -2/(e^x + e^(-x))^2 * (e^x - e^(-x)).
Maintenant, regardons le signe de cette expression. Si x est positif, cela semble simple. Si x est négatif, cela se complique un peu. Donc quittons tout ça. Restons calmes et gardons la tête froide.
Le résultat obtenu est -2e^(2x) + 2. Cela ressemble à une identité remarquable, n'est-ce pas ?
En effet, nous pouvons réécrire cette expression comme -(e^x - 1)^2.
Donc, quel que soit x, cette expression est négative. La fonction g est donc décroissante.
En résumé, nous avons montré que la fonction g(x) = f(x) - x est décroissante. Nous pouvons donc construire un tableau simple pour g :
- Les limites de g en +∞ et -∞ valent +∞ et -∞ respectivement, ce qui est cohérent.
- g est continue sur R
- 0 est compris entre -∞ et +∞, donc il existe un unique α tel que g(2α) = 0.
En conclusion, l'équation f(x) = x admet une seule solution sur R.
Révisions Maths lycée
Analyse Terminale
BCPST

Dérivabilité avec valeur absolue ?
Le cours concerne la démonstration de la continuité et de la dérivabilité d'une fonction f(x), qui est une transcription d'une vidéo.
La première partie du cours explique le potentiel problème de valeur absolue lorsque x=0, car la valeur absolue n'est pas dérivable en 0. Cependant, la fonction 1+x n'est jamais égale à 0, ce qui signifie qu'il n'y a pas de problème de définition et le quotient des deux fonctions est donc continue.
Ensuite, le cours mentionne que la fonction semble également dérivable, sauf en x=0. Cela est démontré en montrant que la fonction est dérivable sur tous les autres points.
Dans la partie suivante, il est demandé de déterminer l'expression de la fonction en fonction du signe de x. Une vérification rapide est effectuée au point x=0 pour confirmer la continuité de la fonction.
Ensuite, il est justifié que la fonction est dérivable partout sauf en x=0. Cela est démontré en calculant les nombres dérivés en x=0.
Finalement, le cours conclut que la fonction est bien continue et dérivable.
Révisions Maths lycée
Analyse Terminale
ECG

Déf formelle
La continuité d'une fonction en un point A signifie que la limite de la fonction lorsque x se rapproche de A est égale à f(A). Si cette propriété est vérifiée pour tous les points d'un intervalle, on dit que la fonction est continue sur cet intervalle. La géométrie associée à cette notion est que si l'on trace la fonction, on ne doit pas avoir à lever le stylo. En d'autres termes, la fonction peut être tracée sans interruption. Pour déterminer si une fonction admet une limite finie en un point, on peut visualiser cette notion en choisissant un intervalle autour de ce point et vérifier si toutes les valeurs de la fonction dans cet intervalle sont comprises dans un autre intervalle prédéfini. Si c'est le cas pour n'importe quelle taille d'intervalle, la fonction admet une limite finie et est continue en ce point.
Révisions Maths lycée
Analyse Terminale
ECG

Discontinuités : exemples
La vidéo présente différents exemples de continuité et de discontinuité dans les fonctions mathématiques. La continuité est définie comme une fonction ayant une limite finie en un point, tandis que la discontinuité est basée sur l'absence de définition ou un comportement irrégulier de la fonction.
Le premier exemple de discontinuité est basé sur la non-définition d'un point. Par exemple, la fonction 1/x n'est pas définie en zéro, ce qui entraîne une discontinuité. La fonction peut avoir un comportement divergent à gauche et à droite de zéro.
Le deuxième exemple est une fonction composée de deux paraboles se rapprochant l'une de l'autre. La fonction n'est pas continue en zéro car elle assigne une valeur différente à gauche et à droite, créant un saut dans le graphique. Il est impossible de trouver un couloir dans lequel toutes les valeurs de la fonction sont incluses.
Le dernier exemple présente une fonction dans laquelle un saut se produit en zéro, mais peut être "rattrapé". La fonction sinus(x)/x n'est pas définie en zéro, mais une valeur fixe de 1,7 est attribuée à ce point. Bien que discontinu, cette fonction peut être prolongée par continuité en attribuant une valeur spécifique à ce point.
En résumé, la vidéo explique les concepts de continuité et de discontinuité dans les fonctions mathématiques à l'aide de différents exemples.
Révisions Maths lycée
Analyse Terminale
ECG

Fonctions usuelles
Ce cours est une transcription d'une vidéo qui traite de la continuité des fonctions visuelles. Il explique que la plupart des fonctions visuelles rencontrées depuis le lycée sont continues sur leur intervalle de définition. Les fonctions x puissance n, 1 sur x, racine carrée, valeur absolue, exponentielle, sinus et cosinus sont toutes continues. Les fonctions construites à partir de combinaisons de ces fonctions seront également continues sur leur ensemble de définition approprié.
Les fonctions non continues sont principalement celles construites par morceaux et par branches. Il existe différents types de discontinuités, tels que la discontinuité par définition, les sauts de discontinuité et les discontinuités prolongeables ou non-prolongeables en un point mal placé.
Il est important de comprendre que l'ensemble de définition d'une fonction n'est pas égal à son ensemble de continuité, qui n'est pas non plus égal à son ensemble de dérivabilité. Par exemple, la fonction valeur absolue de x est définie sur l'ensemble des réels, continue sur cet ensemble, mais non dérivable sur cet ensemble. Elle est dérivable sur l'ensemble des réels étoile.
N'hésitez pas à poser des questions dans le forum et rendez-vous dans une prochaine vidéo pour approfondir ces concepts.
Révisions Maths lycée
Analyse Terminale
ECG

Continuité vs dérivabilité
Ce cours explique le lien entre dérivabilité et continuité d'une fonction. Si une fonction est dérivable en un point, alors elle est continue en ce point. Cependant, le contraire n'est pas vrai. La démonstration consiste à montrer que si f est dérivable en A, alors elle est continue en A. On utilise la définition du taux d'accroissement et la limite du taux d'accroissement lorsque x tend vers A est égale à la dérivée de f en A. En manipulant cette expression, on montre que la limite de f lorsque x tend vers A est égale à f en A, ce qui est la définition de la continuité. Cependant, il est important de noter que la dérivabilité ne garantit pas la continuité, et vice versa. Par exemple, la fonction sin(x)/x est définie partout mais pas continue en 0, tandis que la valeur absolue est continue mais pas dérivable en certains points. On peut résumer les trois ensembles (ensemble de définition, ensemble des points de continuité et ensemble des points de dérivabilité) en disant que l'ensemble des points de dérivabilité est contenu dans l'ensemble des points de continuité, qui lui-même est contenu dans l'ensemble de définition. Deux exemples importants à retenir sont la racine carrée en 0 (non dérivable avec une pente infinie) et la valeur absolue (non dérivable avec deux pentes distinctes).
Révisions Maths lycée
Analyse Terminale
ECG

Continuité et suites : Théorème du point fixe
L'étude de la continuité est appliquée à l'étude des suites, avec un théorème fondamental : le théorème du point fixe. Si une fonction f est définie et continue sur un intervalle I et si une suite un est définie de telle manière que pour chaque n, un appartient à I et un+1 est égal à f(un), alors si un converge vers l (l dans I), on a f(l) = l. Ce résultat est intuitif car lorsque n tend vers l'infini, un tend vers l et donc f(un) tend vers f(l). Cependant, il faut noter que la continuité de la fonction est nécessaire pour que ce résultat soit valide. La démonstration repose sur l'application de la définition de la continuité et l'unicité de la limite. Il est également rappelé que le comportement de convergence peut varier en fonction de la nature de la fonction, avec des convergences en escalier ou en escargot.
Révisions Maths lycée
Analyse Terminale
ECG

TVI : LE théorème
Le théorème des valeurs intermédiaires est un outil essentiel pour l'étude des fonctions et la résolution d'équations. Il permet de démontrer qu'une équation de la forme f(x) = k possède au moins une solution dans un intervalle donné, même si on ne peut pas trouver de solution exacte.
Le théorème stipule que si f est une fonction continue sur un intervalle [a, b], alors pour tout réel k compris entre f(a) et f(b), l'équation f(x) = k admet au moins une solution c dans l'intervalle [a, b].
Pour illustrer cela, on utilise un graphique représentant la courbe d'une fonction. En traçant la courbe de manière continue entre les points f(a) et f(b), on constate que cette continuité garantit le passage de la courbe à travers toute droite horizontale k tracée entre f(a) et f(b). Ainsi, on est assuré d'avoir au moins une solution pour l'équation f(x) = k.
Si la fonction ne présente pas de zigzags, c'est-à-dire si elle est strictement croissante ou décroissante sur l'intervalle [a, b], il n'y aura qu'une seule solution pour chaque valeur k. Cela peut être utilisé pour déterminer les positions exactes des solutions dans certains cas.
Il est important de citer le théorème des valeurs intermédiaires dans les justifications, en précisant que la continuité de la fonction permet d'affirmer l'existence de solutions. Dans le cas où la fonction présente des zigzags, il est également possible d'utiliser le théorème de la bijection pour déterminer le nombre de solutions sur différents sous-intervalles de [a, b].
Révisions Maths lycée
Analyse Terminale
ECG

Continuité en un Point
Ce cours explique comment trouver la dérivée d'une fonction qui a plusieurs expressions sur différents intervalles. Il souligne que même si la fonction peut être continue, elle peut ne pas être dérivable. Par exemple, pour une fonction f définie par trois expressions sur trois intervalles, il faut d'abord s'assurer qu'elle est définie. Ensuite, on vérifie la continuité de la fonction, en particulier aux points d'extrémité des intervalles. On compare les limites de la fonction lorsque x tend vers ces points d'extrémité avec une valeur f(x). Si les limites des deux côtés sont égales à f(x), alors la fonction est continue. En revanche, si les limites diffèrent, la fonction n'est pas continue à ce point. Ensuite, on aborde la dérivation de la fonction dans les prochaines étapes.
Révisions Maths lycée
Analyse Terminale
ECG

Dérivabilité en un Point
La fonction étudiée dans ce cours est f(x) = |x|^2 + 2x - 3. On commence par expliquer pourquoi cette fonction est continue sur R. C'est parce qu'elle est composée de deux fonctions, à savoir un polynôme et la fonction valeur absolue, qui sont toutes les deux continues. Même si la fonction valeur absolue n'est pas dérivable, elle reste continue. Donc par composition, la fonction f(x) est continue sur R.
Ensuite, on observe le graphique de la fonction pour comprendre son comportement. On remarque que la présence de la valeur absolue crée une discontinuité de pente en certains points. Plus précisément, la fonction n'est pas dérivable en x = -3 et x = 1. Cependant, sur tous les autres points, la fonction est dérivable sans problème.
En conclusion, d'après cette observation graphique, la fonction f(x) est dérivable sur tout l'ensemble des réels R, sauf en x = -3 et x = 1.
Révisions Maths lycée
Analyse Terminale
ECG

Prolongement par Continuité
Le prolongement par continuité est utilisé lorsque certaines conditions sont réunies. Tout d'abord, si la fonction n'est pas définie en un point (par exemple en raison d'une valeur interdite), et que la limite de la fonction existe et est finie, on peut effectuer un prolongement par continuité en posant la valeur de la fonction en ce point égale à la limite de la fonction lorsque x tend vers ce point. Cela permet de créer une fonction qui est définie et continue en ce point.
Par exemple, si on considère la fonction f(x) = x/x, on constate qu'elle n'est pas définie en x=0 en raison du dénominateur. Cependant, on peut prolonger cette fonction par continuité en posant f(0)=1, car la limite de la fonction lorsque x tend vers 0 est égale à 1. Ainsi, on obtient une fonction qui est définie et continue en tout point.
Dans l'exercice présenté, on nous propose une fonction f(x) = {0 si x≠0, x*sin(1/x) si x=0}. On constate que cette fonction n'est pas définie en x=0 à cause du terme 1/x. Cependant, en observant le graphique de la fonction, on peut conjecturer que cette fonction est continue en 0, car elle semble se rapprocher de 0 lorsque x tend vers 0. Pour démontrer cela, on utilise le théorème d'encadrement en observant que le terme sin(1/x) est compris entre -1 et 1. En multipliant cette expression par |x|, on obtient une expression qui est comprise entre 0 et x. Puisque cette expression tend vers 0 lorsque x tend vers 0, le théorème d'encadrement nous permet de conclure que la fonction f(x) tend vers 0 lorsque x tend vers 0. Ainsi, on démontre que la fonction f(x) est continuellement 0 en 0, ce qui confirme qu'il s'agissait bien d'un prolongement par continuité proposé par l'exercice.
En résumé, le prolongement par continuité est utilisé lorsque la fonction n'est pas définie en un point mais que sa limite existe. En posant la valeur de la fonction égale à cette limite, on obtient une fonction qui est définie et continue en ce point. Dans l'exercice présenté, on démontre que la fonction proposée est continuellement 0 en 0 en utilisant le théorème d'encadrement.
Révisions Maths lycée
Analyse Terminale
ECG

TVI et Fonction Auxiliaire
Le cours porte sur le théorème des valeurs intermédiaires et son utilisation pour étudier une fonction complexe.
La fonction étudiée, f(x) = 10x / (e^x + 1), est bien définie et dérivable sur l'ensemble de définition (0 ; +∞). La dérivée de f(x) est obtenue en utilisant la formule du quotient, et simplifiée pour obtenir la fonction g(x) = 1 - xe^x.
Pour appliquer le théorème des valeurs intermédiaires, il est nécessaire de vérifier la continuité de g(x) sur l'intervalle (0 ; +∞), ce qui est le cas ici. On trouve que g(0) = 2 et que la limite de g(x) lorsque x tend vers +∞ est -∞. Ainsi, la fonction g(x) passe par 0, ce qui permet d'utiliser le théorème des valeurs intermédiaires.
En dérivant g(x) on obtient g'(x) = -xe^x, qui est strictement négative sur l'intervalle (0 ; +∞). On en déduit que la fonction g(x) est strictement décroissante.
L'application du théorème des valeurs intermédiaires permet de conclure qu'il existe un unique réel alpha tel que g(alpha) = 0. En utilisant une calculatrice, on trouve que alpha ≈ 1,28.
Le signe de g(x) permet de déterminer le sens de variation de f(x). On trouve que f(x) est croissante sur l'intervalle (0 ; alpha) et décroissante sur l'intervalle (alpha ; +∞). Les limites de f(x) sont f(0) = 0 et f(x) tend vers 0 lorsque x tend vers +∞.
En conclusion, le théorème des valeurs intermédiaires permet d'affirmer l'existence et l'unicité d'un réel alpha tel que f(alpha) = 0, et d'obtenir le sens de variation de f(x) sur l'intervalle (0 ; +∞).
Révisions Maths lycée
Analyse Terminale
ECG

Continuité et suites 1
Dans cette méthode, nous étudions le calcul d'une limite lorsque la suite est définie par récurrence. Il s'agit des suites dites "en escalier". Pour trouver la limite et la justifier, il est essentiel de vérifier certaines hypothèses. La méthode consiste à considérer une suite spécifique définie par u0 = 1 et un+1 = u^n * (e^2 - u). Il est important de noter que la convergence peut dépendre du premier terme. Ainsi, si une suite définie par récurrence de la forme un+1 = f(un) converge vers une limite L, alors un+1 converge aussi vers L. Cela permet de passer à la limite de l'équation un+1 = f(un) en considérant que la limite de un+1 est L et que la limite de un, étant donné que un converge vers L, est f(L). Par conséquent, L est nécessairement un point fixe de l'équation f(x) = x. Cependant, cette assertion n'est vraie que si f est une fonction continue. Il est donc essentiel de justifier la continuité. L'énoncé suppose la convergence vers L, mais il ne justifie pas pourquoi. Cependant, c'est cette hypothèse qui permet de conclure que la limite est parmi les points fixes de f(x) = x. Si aucun point fixe n'existe, il n'y aura pas de limite pour cette suite définie par récurrence avec une relation de type un+1 = f(un). Dans cet exemple spécifique, on cherche les points fixes de la fonction f(x) = x * (e^2 - x). On trouve que la seule solution est x = 0. Comme nous supposons que la suite converge, c'est la seule possible limite. Graphiquement, on peut représenter cette suite en utilisant une construction en escalier, où chaque terme un est reporté sur l'axe des abscisses. On peut voir que la suite converge vers 0, mais cela dépend du premier terme u0. Si u0 est positif, la suite converge, sinon elle diverge vers moins l'infini. Ainsi, le premier terme est essentiel. Enfin, la continuité est essentielle dans ce type de fonction. Un exemple de fonction discontinue est présenté, où une suite particulière converge vers a sans jamais être égale à a. Cela montre qu'en l'absence de continuité, l'égalité limite de f(un+) = f(limite de un) ne s'applique pas. Il est donc crucial d'avoir la continuité pour utiliser cette méthode de calcul de limite.
Révisions Maths lycée
Analyse Terminale
ECG

Continuité et Suites 2
Dans ce cours, on étudie une suite définie par récurrence et on cherche à trouver sa limite. On associe une fonction f à la suite et on étudie la continuité de cette fonction. Ensuite, on résout l'équation f(x) = x pour trouver les solutions possibles. On étudie également la dérivabilité de la fonction f et on montre qu'elle est croissante sur certains intervalles. On utilise ensuite la méthode de récurrence pour montrer que les termes de la suite sont compris entre 0.5 et 3. On conclut que la suite est croissante et bornée, donc elle est convergente. On utilise ensuite la continuité de f pour montrer que la limite de la suite est une solution de l'équation f(x) = x. On trouve que la limite doit être 1. On explique ensuite pourquoi la continuité de f est importante en montrant un contre-exemple où la suite converge vers 1 mais ne satisfait pas l'équation f(x) = x. On conclut en résumant la méthode utilisée pour trouver la limite des suites définies par récurrence et en proposant des exercices d'entraînement.
Révisions Maths lycée
Analyse Terminale
ECG
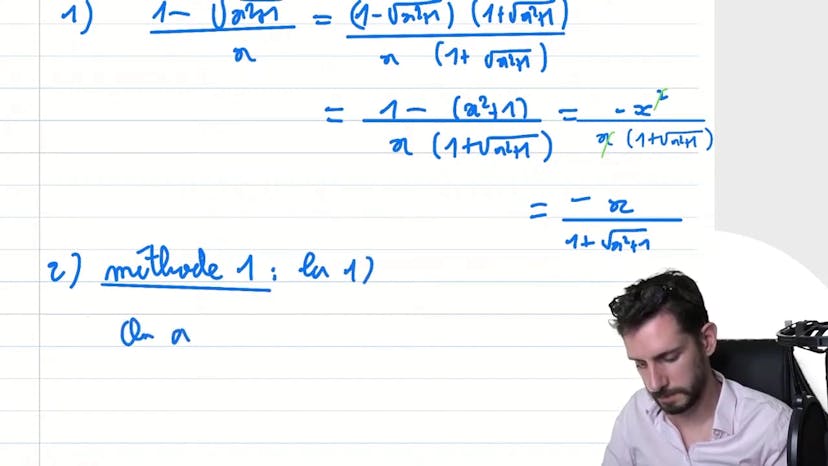
Saut de continuité
Le cours traite de la continuité d'une fonction définie par une valeur différente de zéro pour les valeurs de x différentes de zéro, et une valeur m quand x est égal à zéro. Pour déterminer si la fonction est continue, il est nécessaire de vérifier si le petit point introduit dans la fonction créé une situation où la fonction ne peut pas être tracée sans lever le stylo, ou si le petit point est positionné de manière à ce que la fonction puisse être tracée sans interruption. Deux méthodes sont utilisées pour déterminer la continuité de la fonction : la méthode de la quantité conjuguée et la méthode du taux d'accroissement. Dans le premier exercice, la méthode de la quantité conjuguée est utilisée pour simplifier une forme indéterminée et montrer que la fonction est continue. Dans le deuxième exercice, la méthode du taux d'accroissement est utilisée pour déterminer la continuité de la fonction en 0 et trouver la valeur de m qui rend la fonction continue en ce point. La réponse à la question b est que m doit être égal à 0 pour que la fonction soit continue en 0.
Révisions Maths lycée
Analyse Terminale
ECG

TVI et expo
L'objectif de ce cours est d'étudier le nombre de solutions d'une équation. Graphiquement, on observe les fonctions E-x² et E2x-1. La première est une courbe en forme de cloche et la seconde est une fonction exponentielle décalée d'une unité sur l'axe Y. On remarque qu'il semble y avoir une solution à environ 0.552. On observe également que pour les nombres négatifs, la fonction noire est au-dessus de la fonction rouge, tandis que pour les nombres positifs, elles s'intersectent à un certain point.
Pour montrer qu'il y a une solution pour tout réel négatif, on utilise le fait que la fonction E2x-1 est strictement inférieure à la fonction E2-x². Donc, elles ne se croisent pas et il n'y a pas de solution.
Ensuite, on se concentre sur les nombres positifs. On montre que la fonction f2x = E2x-1 est strictement décroissante sur l'intervalle [0, +∞]. On peut le démontrer en écrivant f2x = E2-x² sur l'intervalle [0, +∞]. On utilise également le fait que l'exponentielle est décroissante. Donc, f est négative et décroissante sur cet intervalle.
En utilisant le théorème des valeurs intermédiaires, on peut conclure qu'il existe une unique solution à l'équation sur l'intervalle des nombres positifs.
En résumé, il n'y a pas de solution pour les nombres négatifs, mais il y a une unique solution pour les nombres positifs. Ce résultat est conforme à ce que nous avions observé graphiquement.
Révisions Maths lycée
Analyse Terminale
ECG

TVI et calculs costauds !
Dans ce cours, nous étudions la fonction f(x) = 2/(e^x + e^(-x)). Notre premier réflexe est de vérifier si la fonction est bien définie, c'est-à-dire si le dénominateur peut être nul. Comme il s'agit d'une somme d'exponentielles positives et strictement positives, le dénominateur ne peut jamais être nul. Donc, nous sommes confiants quant à la définition de la fonction.
Ensuite, nous examinons graphiquement le nombre de solutions de l'équation f(x) = x. Nous observons qu'il y a une seule solution.
Pour prouver que la fonction g(x) = f(x) - x est décroissante, nous commençons par vérifier si elle peut être exprimée comme la somme de fonctions décroissantes. Malheureusement, cela ne fonctionne pas, donc nous devons passer par un calcul de dérivées.
Nous calculons la dérivée de f(x), qui est un peu compliquée mais faisable. Nous mettons tout au même dénominateur et nous obtenons l'expression simplifiée de la dérivée.
En analysant cette dérivée, nous remarquons que nous avons une somme d'exponentielles de x et d'autres termes qui forment des identités remarquables. Nous recomposons ces identités remarquables et nous obtenons finalement l'expression g(x) = (e^(2x) + 1)^2 - (e^(-x) - 1)^2. Nous remarquons que g(x) est toujours négatif, ce qui prouve que la fonction g est décroissante.
Finalement, nous faisons un petit tableau pour la fonction g, en prenant en compte ses limites (plus l'infini et moins l'infini), sa décroissance stricte et le fait que 0 est compris entre moins l'infini et plus l'infini. Grâce au théorème des valeurs intermédiaires, nous concluons qu'il existe un unique alpha tel que g(2x) = 0, ce qui signifie qu'il y a une seule solution à l'équation f(x) = x.
Révisions Maths lycée
Analyse Terminale
ECG

Dérivabilité avec valeur absolue ?
Dans cet exercice, il est question de déterminer si une fonction est continue et dérivable sur R. La fonction en question est définie comme suit : f(x) = 1 + x / |x|.
Tout d'abord, pour analyser la continuité de la fonction, on remarque que 1 + x est définie pour tout x appartenant à R. De plus, |x| est toujours strictement positive, donc l'expression 1 + x / |x| ne peut jamais être égale à zéro. Ainsi, il n'y a pas de problème de définition et la fonction est continue sur tout R.
En ce qui concerne la dérivabilité de la fonction, on constate qu'elle est dérivable partout sauf en x = 0. En effet, la dérivée de 1 + x est simplement 1, et la dérivée de |x| est indéfinie en x = 0. Cependant, on suppose que la fonction est dérivable en x = 0 par intuition, car elle semble lisse et ne présente pas de rupture de pente à ce point.
Pour démontrer la dérivabilité de la fonction, on calcule ses dérivées de chaque côté de x = 0. À droite de 0, la dérivée de f(x) est égale à 2x / (1 + x)^2. À gauche de 0, la dérivée de f(x) est égale à x - 1 / (1 - x)^2. En évaluant ces dérivées en x = 0, on obtient respectivement 0 et 1. Donc, les dérivées à gauche et à droite de 0 ne sont pas égales, ce qui signifie que la fonction n'est pas dérivable en x = 0.
En conclusion, la fonction f(x) = 1 + x / |x| est continue sur tout R, mais n'est pas dérivable en x = 0.


