 All subjects
All subjects
 All subjects
All subjects
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Intro Convergence
Bienvenue dans ce dernier sujet du chapitre sur les suites, les théorèmes de convergences. Les théorèmes de convergence nous permettent de mieux comprendre et analyser certaines suites qui peuvent sembler complexes. Nous pouvons observer que certaines fractions sont divisées par des valeurs de plus en plus grandes, ce qui peut sembler rendre la suite difficile à gérer. Cependant, si nous examinons de plus près, nous pouvons remarquer que ces nombres restent très petits. Malgré leur apparence complexe, ils se rapprochent de zéro. Nous pouvons également le voir graphiquement grâce à la fonction sinusex sur x et la suite sinusène sur n. Bien que la suite oscille, elle s'approche de plus en plus de zéro. Les théorèmes de convergences nous permettent d'analyser ces suites complexes en les comparant à des suites plus simples pour en tirer des conclusions. Parmi les théorèmes importants qui nous aideront à trouver les limites des suites, il y a le théorème de comparaison et le théorème de gendarme. Le premier est utilisé pour démontrer que quelque chose tend vers l'infini, tandis que le second est utilisé pour montrer qu'une suite tend vers une limite finie. Nous verrons également quelques définitions telles que les suites minorées, majorées et bornées. Enfin, nous étudierons le théorème de convergence monotone, ainsi que des méthodes pratiques pour gérer les suites comportant des sinus ou des puissances négatives. Nous aborderons également un cas courant : les suites homographiques. Cette vidéo nous prépare également à la prochaine vidéo qui sera consacrée au théorème de comparaison. N'hésitez pas à poser vos questions dans la FAQ. À bientôt !
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Théorème de comparaison - Illustration
Le théorème de comparaison en analyse mathématique est un outil puissant qui permet de simplifier les démonstrations en se basant sur des suites comparables. En effet, si on a une suite Vn qu'on ne sait pas traiter directement, mais qu'on peut comparer à une suite plus simple Un qui tend vers l'infini, alors on peut en déduire que Vn suit le même comportement. Par exemple, si on peut montrer que Vn est toujours plus grand que Un, et que Un tend vers l'infini, alors Vn aussi.
Cela permet d'éviter des calculs compliqués avec des epsilon et d'autres paramètres peu attrayants. On peut ainsi conclure que Vn suit la même tendance que Un sans avoir à étudier en détail la forme particulière de Vn. Ce théorème est particulièrement utile lorsque la suite Vn a une forme difficile à manipuler, comme dans l'exemple donné, où Vn est égal à l'exponentielle de la racine de n² plus 1.
Pour illustrer le théorème de comparaison, on prend l'exemple de racine de n² plus 1, qui est plus grand que racine de n² (n étant un entier). En utilisant l'exponentielle et en montrant que l'exponentielle de racine de n² plus 1 est plus grand que l'exponentielle de n, on peut conclure que Vn suit une croissance exponentielle et tend vers l'infini, car l'exponentielle de n est une suite géométrique de raison supérieure à 1.
Ce théorème permet donc d'éviter des calculs complexes et de simplifier les démonstrations en se basant sur des comparaisons entre suites simples et suites plus complexes. Son utilité réside dans le fait qu'il permet d'aboutir à une conclusion sans avoir à étudier en détail la forme de la suite complexe.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Théorème de comparaison - démonstration
Dans ce cours, nous démontrons le théorème qui nous permet de simplifier nos démonstrations en utilisant une notation plus simple. Nous commençons par rappeler la définition de "tendre vers plus infini" pour une suite. Ensuite, nous traduisons l'énoncé du théorème en langage mathématique. Si la limite de la suite Un lorsque n tend vers plus infini est égale à plus infini, alors quelque chose se produit. Plus précisément, pour tout nombre positif A, il existe un rang N à partir duquel tous les termes de la suite Un sont supérieurs à A. Nous utilisons cette propriété pour conclure que pour tout N plus grand ou égal à un certain grand N, les termes de la suite Vn sont également supérieurs ou égaux à A. En résumé, pour tout nombre positif A, il existe un rang N à partir duquel tous les termes de la suite Vn sont supérieurs ou égaux à A. Cette conclusion correspond à la définition de la divergence vers plus infini. En utilisant cette démonstration, nous n'avons plus besoin d'utiliser les démonstrations avec les démonstrations en epsilon, en grand A, etc. Vous pouvez poser des questions dans la FAQ si vous avez des doutes.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Théorème des gendarmes
Le théorème d'encadrement, également appelé théorème des gendarmes, est l'équivalent du théorème de comparaison pour les limites finies. Ce théorème permet de montrer qu'une suite VN converge vers un réel fini L en la comparant à deux autres suites UN et WN, telle que UN est inférieure à VN et WN. Si les suites VN et WN convergent vers la même limite L, alors la suite UN converge également vers L.
Ce théorème est très pratique car il permet d'obtenir des résultats sur les suites sans se soucier des définitions formelles d'ε et d'A. Il peut être illustré avec un exemple tel que la suite sinus n/n, qui peut être difficile à gérer. Cependant, en encadrant cette suite entre les suites 1/n et -1/n, qui convergent toutes les deux vers zéro, on peut conclure que la suite sinus n/n converge également vers zéro.
Il est important de noter que tous les cas ne sont pas aussi simples et qu'il est parfois difficile de tirer des conclusions. Cependant, on peut dire de manière intuitive que si deux suites ordonnées UN et VN convergent, alors leurs limites seront également ordonnées, c'est-à-dire que la limite de VN sera inférieure à la limite de VN.
En résumé, le théorème d'encadrement permet de prouver que les limites finies des suites en les comparant à des suites inférieures et supérieures convergentes. Cela facilite l'analyse des suites et offre des résultats pratiques.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Suite majorée, minorée & Th de convergence monotone
Le cours porte sur les théorèmes de convergence. Il explique les définitions de base pour comprendre ces théorèmes. On dit qu'une suite est majorée lorsqu'elle est toujours bloquée par une certaine valeur et toutes les valeurs au-dessus. Il peut y avoir plusieurs valeurs bloquant la suite, mais il y en aura toujours une infinité. On dit qu'une suite est minorée lorsqu'elle ne peut pas descendre en dessous d'une certaine valeur. De même, il peut y avoir plusieurs valeurs bloquant la suite vers le bas. Lorsqu'une suite est à la fois majorée et minorée, on dit qu'elle est bornée.
Le cours illustre ces concepts avec des exemples graphiques de suites bornées. Il explique également le théorème de convergence monotone, qui dit que si une suite est croissante et majorée, alors elle converge. Cependant, il souligne que ce théorème ne permet pas de trouver la limite de la suite, mais seulement de déterminer si elle converge.
Le cours aborde également la réciproque du théorème de convergence monotone, qui est fausse. Il montre des contre-exemples de suites qui convergent sans être croissantes ou décroissantes. Il insiste sur l'importance de comprendre ces contre-exemples pour ne pas se faire piéger lors des exercices ou des questions de cours.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Th convergence monotone - démo
Dans cette vidéo, on fait une démonstration du théorème de convergence monotone dans le cas où on a une suite croissante non majorée. On explique que si la suite croissante n'est jamais bloquée et tend à augmenter constamment, alors elle tend vers plus l'infini. On donne la définition formelle de la convergence vers plus l'infini et on montre qu'elle est quasiment identique à la démonstration faite précédemment. On commence en fixant un nombre positif A. Ensuite, on démontre que pour ce A fixé, il existe toujours un certain rang à partir duquel la suite est au-dessus de A, c'est-à-dire que tout grand A finira par se faire dépasser. On combine le fait que la suite n'est pas majorée avec le fait qu'elle est croissante pour montrer que pour tout N au-dessus d'un certain rang P, chaque terme de la suite sera plus grand que A. Ainsi, on a montré que pour tout A fixé, la suite finira toujours par être au-dessus de A, ce qui correspond à la définition de convergence vers plus l'infini. On conclut en disant qu'on a démontré le théorème et en laissant les spectateurs sur cette note, en les invitant à revenir pour la prochaine vidéo.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Encadrer sin(n)
Dans ce cours, nous appliquons les théorèmes de convergence aux fonctions sinus et moins 1 puissance n. Nous étudions la suite un qui est égale à n plus 2 fois sin n. L'exercice nous demande de montrer que pour tout n, un est supérieur à n-2. Pour cela, nous utilisons l'encadrement du sinus entre -1 et 1. Puis nous multiplions par 2 et ajoutons n pour obtenir un. Ainsi, un est compris entre n-2 et n+2. Ce qui nous intéresse vraiment, c'est la partie où un est supérieur à n-2. En utilisant la limite usuelle, nous montrons que n-2 tend vers moins l'infini et que un est plus grand qu'une suite qui tend vers l'infini. Donc, par comparaison, un tend vers l'infini.
Dans le deuxième exemple, nous avons la suite Vn qui est égale à moins n carré moins n plus moins 1 puissance n. Nous encadrons encore une fois le moins 1 puissance n entre -1 et 1. En analysant la suite, nous constatons que le terme dominant est moins n carré. Ainsi, le terme moins 1 puissance n ne nous gêne pas beaucoup. Nous démontrons cela par l'encadrement, en ajoutant moins n carré moins n à la suite Vn. Finalement, nous obtenons que Vn est inférieur à une suite qui tend vers moins l'infini. En factorisant et en examinant les limites, nous concluons que Vn tend vers moins l'infini.
Ainsi, ces deux exemples nous montrent comment utiliser l'encadrement pour des suites impliquant le sinus ou moins 1 puissance n.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
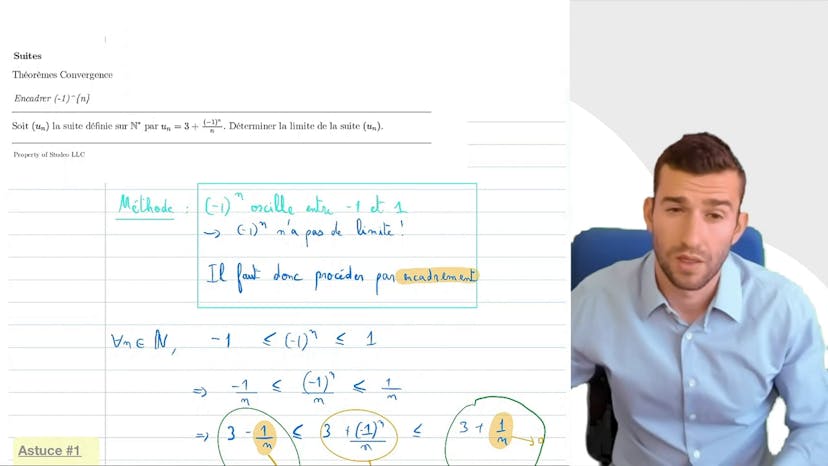
Encadrer (-1)^n
Dans ce cours, nous avons étudié une autre type de suite nécessitant un encadrement. Il s'agit des suites où il y a un "-1 puissance n" inclus. Dans ce cas, il n'y a pas de limite pour "-1 puissance n", donc nous utilisons l'encadrement pour déterminer la limite de la suite UN.
Dans ce cas précis, UN est égal à 3 plus "-1 puissance n sur n". En raison du terme "-1 puissance n sur n", qui tend vers 0 en raison du facteur "sur n", nous pouvons voir que UN tend vers 3. Nous prouvons cela par encadrement. En partant de l'encadrement de "-1 puissance n", nous multiplions ensuite par un sur n, qui est positif, ce qui ne change pas le sens des inégalités, et nous ajoutons 3.
Ainsi, nous avons 3 moins 1 sur n, qui est plus petit que UN, qui est plus petit que 3 plus 1 sur n. Par conséquent, le terme de gauche tend vers 3, tout comme le terme de droite. Selon le théorème d'encadrement, nous en concluons que UN tend vers 3.
Il est important de souligner que le théorème d'encadrement permet non seulement de prouver la convergence, mais aussi de trouver la limite, ce qui en fait un théorème très puissant. Grâce à l'encadrement, nous avons donc montré que UN tend vers 3.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Exo TRÈS classique
Dans cette leçon, nous avons étudié une méthode pour trouver la limite d'une suite qui est une fonction rationnelle. Nous avons examiné le cas où le degré du numérateur est égal au degré du dénominateur, et la limite est alors le quotient des coefficients dominants de ces deux polynômes. Cependant, au lieu de nous intéresser à la limite elle-même, nous avons montré des résultats préliminaires tels que la majoration et la croissance de la suite, à partir desquels nous pouvons conclure sur sa convergence en utilisant les théorèmes de convergence.
Dans le premier exercice, nous nous sommes intéressés à la majoration de la suite Un=n-1 / (n+4) et avons montré qu'elle est inférieure à 1. Ensuite, nous avons étudié la monotonie de la suite, en regardant Un+1 - Un, et avons conclu que la suite est strictement croissante. Ensuite, nous avons montré que la suite est à la fois croissante et majorée, ce qui implique qu'elle est convergente. Cependant, nous ne pouvons pas déduire la limite à partir de ces résultats.
Ensuite, nous avons examiné un autre exemple avec la suite Un=2n-2 / (n+4). En utilisant la méthode précédente, nous avons montré que la suite est majorée par 2 et que la suite est strictement croissante. Cela implique que la suite est convergente, mais encore une fois, nous ne pouvons pas conclure sur la limite.
En conclusion, cette méthode nous permet de montrer la convergence d'une suite rationnelle en montrant sa majoration et sa croissance, mais elle ne nous permet pas de déterminer la limite. Il est important de noter que la limite n'est pas nécessairement le majorant trouvé, et que la suite peut converger vers une valeur inférieure.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Introduction Convergence
Dans ce nouveau sous-chapitre sur les limites de fonctions, nous abordons des concepts plus pratiques et concrets. Il est important de connaître par cœur certains tableaux de fonctions de référence, par exemple la limite de 1 sur x en plus infini. Nous étudions également comment combiner des limites, par exemple la limite de f plus g. Certaines situations, comme lorsque f tend vers plus infini et g tend vers moins infini, nécessitent une étude plus approfondie. Nous examinons le rapport f sur g et le produit f fois g, en appliquant des règles spécifiques. Il y a quatre formes indéterminées pour lesquelles il n'y a pas de règles préétablies. Nous abordons également les théorèmes de convergence, tels que le théorème des gendarmes, dans lequel deux fonctions encadrent une troisième fonction pour la mener vers la même limite finie. Le théorème de comparaison est utilisé pour les limites infinies, où si une fonction f est inférieure à une fonction g et que f tend vers plus infini quelque part, g la suit également. Nous parlons également de la croissance comparée, en se concentrant sur l'exponentielle et discutons de la limite de composé, qui permet de gérer des fonctions complexes. Il faut également connaître les tableaux de référence pour les fonctions de référence, les opérations sur les limites et les quatre formes indéterminées. En termes de méthode, nous apprenons à gérer les formes indéterminées en utilisant des techniques telles que le terme du plus haut degré et la méthode de quantité conjuguée. En conclusion, en maîtrisant ces points de cours et les méthodes associées, vous serez prêts à aborder les différentes limites qui vous seront présentées. N'hésitez pas à poser des questions dans la FAQ si nécessaire.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Tableaux : fonctions de référence
Dans cette vidéo, nous faisons un bilan des différentes fonctions de référence et de leurs limites, ainsi que des règles de combinaison de ces limites. Nous commençons par étudier la fonction 1/x. La limite de cette fonction est plus l'infini lorsque x tend vers 0 à partir de valeurs positives, et moins l'infini lorsque x tend vers 0 à partir de valeurs négatives. Ensuite, nous examinons les limites de la fonction x^n, où n est un nombre entier. Lorsque x tend vers plus l'infini, cette fonction tend également vers plus l'infini. Si n est pair, la fonction reste positive quel que soit x. Si n est impair, la fonction change de signe selon le signe de x. Nous parlons ensuite des fonctions exponentielles et racines. L'exponentielle de x tend vers plus l'infini lorsque x tend vers plus l'infini, et vers 0 lorsque x tend vers moins l'infini. L'exponentielle de -x est symétrique par rapport à l'axe des ordonnées. La racine de x tend vers 0 en plus l'infini, et 1 sur la racine de x tend vers 0 en plus l'infini également. En conclusion, il est important de comprendre ces différentes fonctions et leurs limites pour résoudre des exercices de calcul.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Tableaux : combiner des limites
La prochaine étape consiste à étudier les limites des fonctions, notamment les limites d'une somme et d'un produit. Il existe plusieurs cas simples à prendre en compte. Lorsque deux fonctions, f et g, tendent chacune vers une limite L et L', respectivement, la limite de leur somme est L + L' et la limite de leur produit est L * L'. Ensuite, si L est une limite finie et qu'il est ajouté ou soustrait à une limite infinie, c'est toujours l'infini qui l'emportera. Pour le produit, cela dépendra du signe de L. Si L est positif, la limite tendra vers l'infini inversé, alors que si L est négatif, la limite tendra vers l'infini. Il faut garder à l'esprit que ces exemples suivent des règles de signes : plus et plus font plus, plus et moins font moins, et moins et moins font plus. Les cas où il est écrit "fi" représentent des cas indéterminés, c'est-à-dire des situations où il est impossible de déterminer la limite. Ces cas incluent la multiplication de 0 par l'infini et l'addition de plus l'infini et moins l'infini.
Une forme indéterminée signifie qu'il n'y a pas de règle générale qui s'applique dans toutes les situations. Pour illustrer cela, prenons l'exemple de l'addition de plus l'infini et moins l'infini. Selon les fonctions choisies, comme x, x^2 et x, les résultats peuvent varier et seront sans rapport les uns avec les autres. C'est ce qui rend une forme indéterminée : il n'y a pas de résultat prédéterminé, tout peut se produire.
En ce qui concerne le quotient, si l'on divise deux fonctions f et g, on obtient une limite l sur l'axe des x et L' sur l'axe des y, si f et g tendent respectivement vers L et L'. Il existe des règles évidentes à suivre : si la limite de f est L et la limite de g tend vers l'infini, le résultat sera très grand, donc la limite sera de 0. Si la limite de f est L et la limite de g est 0, le résultat sera plus ou moins l'infini, comme nous l'avons déjà vu avec l'exemple de 1/x.
En conclusion, il existe deux formes indéterminées à retenir : 0 sur 0 et plus l'infini sur plus l'infini. Ces formes indéterminées peuvent donner différents résultats selon les fonctions choisies. Il est important de s'entraîner à créer des exemples simples pour bien comprendre ces concepts. Il est également crucial de se rappeler que les formes indéterminées signifient qu'il n'y a pas de règle générale, et que tout est possible. En résumé, les formes indéterminées sont les aspects les plus importants à retenir lors de l'étude des limites des fonctions.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Comparaison et encadrement
Le cours résume les deux théorèmes de comparaison et d'encadrement pour les fonctions. Le premier théorème stipule que si deux fonctions f et g tendent vers plus l'infini et que g est plus grande que f, alors f va pousser g vers plus l'infini. Le deuxième théorème, appelé théorème des gendarmes, dit que si f et h encadrent une fonction g et que f et h tendent vers la même limite, alors g tend également vers cette limite. Des exemples graphiques ont été donnés pour illustrer ces théorèmes.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
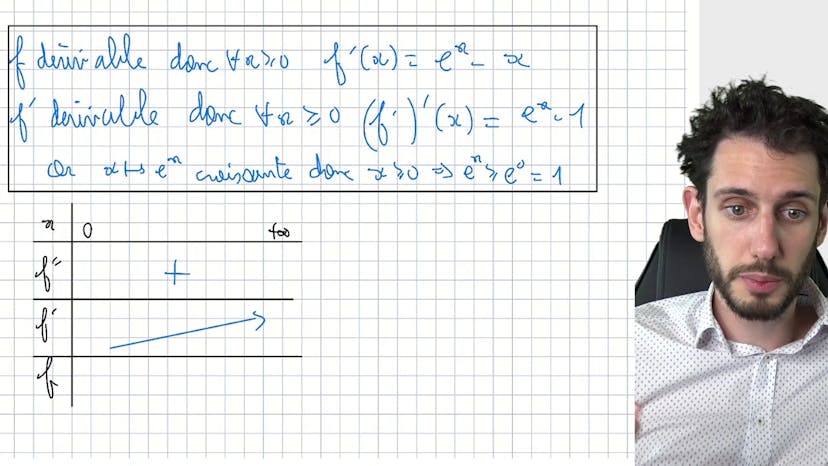
Croissance comparée exp et ln
Dans ce sous-chapitre sur les limites de fonctions, il est abordé le concept de croissance comparée. En résumé, la croissance comparée est l'idée que la fonction exponentielle domine n'importe quelle puissance de x. Cela signifie que quand on divise l'exponentielle e^2x par x^n, la limite de cette expression tend vers l'infini. La possibilité d'utiliser cette propriété est démontrée en montrant que la fonction f(x) = e^2x - (x^2)/2 est toujours positive. En utilisant cette démonstration, on peut alors prouver que e^x/x^n tend vers l'infini. De plus, il est également démontré que e^(-x)/x^n tend vers 0 quand x tend vers moins l'infini. Ces démonstrations utilisent des changements de variables simples pour simplifier les expressions et appliquer les propriétés des puissances. Il est souligné que ces méthodes peuvent être utiles non seulement dans le contexte de ces démonstrations, mais aussi dans d'autres calculs de limites ou exercices.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Limite des fonctions composées
Le cours porte sur les limites de fonctions, en se concentrant sur le concept de composition. Le professeur donne un exemple concret et simple pour illustrer l'idée de composition. Il explique que la composition consiste à décomposer une fonction en plusieurs morceaux et montre comment cela s'applique à l'exemple donné.
Il souligne également l'importance de démontrer les résultats obtenus par composition, en ajoutant que cela nécessite une autorisation théorique. Il promet de revenir sur cette notion plus tard.
En résumé, le cours met en avant l'idée de composition dans le calcul des limites de fonctions et explique comment appliquer cette notion à un exemple spécifique.
Note de l'éditeur : Pour optimiser ce résumé pour le référencement SEO, il serait nécessaire de le réorganiser afin de mettre l'accent sur les mots-clés pertinents pour le contenu donné. Cela pourrait inclure des mots-clés tels que "limites de fonctions", "composition", "démontrer les résultats", "autorisation théorique", etc.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Forme indéterminée : utilisation du terme plus haut degré
La méthode pour déterminer les limites des polynômes et des fonctions rationnelles consiste à factoriser par le terme de plus haut degré, appelé "terme de Claudegris". On applique cette méthode à une première fonction polynomiale G2x, en factorisant par x^4. On obtient alors (1 + 4/x)/(2x^3 - 2/x^3), qui tend vers 1/x^4. Ainsi, la limite de G2x en plus et moins l'infini est plus l'infini.
Pour une fonction rationnelle avec un quotient de deux polynômes, la méthode est la même. On factorise le numérateur et le dénominateur par le terme de Claudegris. Par exemple, pour une fonction h2x avec numérateur 2x^2 et dénominateur (1-x), on obtient (2x / (1-x))(1 + 1/x) qui tend vers 2x / (1-x). En analysant les signes, on détermine que la limite de h2x en moins l'infini est plus l'infini et en plus l'infini, moins l'infini.
En résumé, pour déterminer les limites en plus et moins l'infini des polynômes et des fonctions rationnelles, il suffit de factoriser par le terme de plus haut degré. Cette méthode fonctionne à chaque fois et il est important de la maîtriser.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Forme indéterminée : Méthode quantité conjuguée
La méthode de la quantité conjuguée est une technique classique utilisée lorsque nous avons des racines dans une équation. Lorsque nous ne voulons pas effectuer les calculs avec les racines car elles ne s'additionnent pas facilement, nous pouvons utiliser la quantité conjuguée pour les éliminer.
Nous avons ici un exemple de fonction avec une forme indéterminée lorsque x tend vers 0. Cependant, lorsque x tend vers 0, le terme en question tend vers 1 et la racine de x tend vers 0, ce qui donne 1 sur 1. Donc pour x > 0, il n'y a pas de problème, cela tend vers 1. La racine de x n'étant pas définie pour les valeurs négatives, nous nous concentrons sur les valeurs positives.
En revanche, lorsque x tend vers l'infini, la situation est différente. Sans effectuer de calculs détaillés, nous pouvons voir que cela donne plus l'infini moins l'infini, ce qui est une forme indéterminée. Les racines ne se factorisent pas facilement entre elles, donc nous utilisons la quantité conjuguée. En multipliant le numérateur et le dénominateur par la quantité conjuguée, les racines disparaissent en bas mais apparaissent en haut. Cependant, cela est avantageux car cela transforme le signe moins en un signe plus, ce qui résout le problème de l'indétermination.
Ainsi, nous obtenons x plus 1 moins x au dénominateur, ce qui simplifie à x plus 1. Finalement, le dénominateur devient 1 et la fonction devient la somme de deux racines de x, ce qui n'est plus une forme indéterminée. Donc, lorsque les racines diffèrent, il est conseillé d'utiliser la quantité conjuguée car cela élimine automatiquement l'indétermination. Voilà donc l'utilité de cette méthode classique pour les limites avec racines.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Limites : la Croissance comparée
La méthode de la croissance comparée est une technique très utile en mathématiques. Elle consiste à comparer la croissance de différentes fonctions pour déterminer le comportement de ces fonctions lorsque la variable tend vers l'infini ou moins l'infini.
Dans cette transcription, l'auteur utilise cette méthode pour étudier deux fonctions, e de x sur x et x puissance 4 sur e de x.
Pour la première fonction, e de x sur x, il montre que lorsque x tend vers moins l'infini, la fonction tend vers 0, car e de x tend vers 0 et x sur moins l'infini est toujours égal à 0. Lorsque x tend vers plus l'infini, il dit que par croissance comparée, e de x l'emporte sur toute puissance de x et donc la fonction tend vers plus l'infini.
Pour la deuxième fonction, x puissance 4 sur e de x, l'auteur fait un changement de variable astucieux en posant grand x égal à moins l'infini plus petit x. Ainsi, il peut écrire x sur e de x comme l'inverse de la croissance comparée de référence, qui tend vers 0. Par composition des limites, il conclut que la fonction tend vers 0.
En résumé, la méthode de la croissance comparée permet de déterminer le comportement de fonctions lorsque la variable tend vers l'infini ou moins l'infini. Grâce à cette méthode, on peut conclure que e de x sur x tend vers plus l'infini lorsque x tend vers plus l'infini, et que x puissance 4 sur e de x tend vers 0 lorsque x tend vers moins l'infini. Cette méthode est utile pour lever rapidement la détermination dans des calculs mathématiques.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Double racine
Bonjour à tous, dans cet exercice sur les limites, nous devons montrer que la fonction f est définie sur l'ensemble des réels. Pour cela, nous examinons les racines de la fonction. Pour la première racine, nous remarquons que x² et 1+x² sont toujours strictement positifs, donc il n'y a pas de problème. En ce qui concerne la deuxième racine, nous devons faire deux cas : si x > 0, alors x est positif et 1+x² est positif, donc pas de problème. Si x < 0, nous comparons les deux termes et remarquons que 1+x² est plus grand que x², donc racine(1+x²) est bien défini et positif. Ainsi, les racines sont définies pour tout x appartenant à R, donc l'ensemble de définition de f est R.
Pour la deuxième question, nous devons justifier que f est dérivable sur tout R. Pour cela, nous devons montrer que l'intérieur des racines est strictement positif. En utilisant les inégalités précédentes, nous pouvons conclure que l'intérieur des racines est strictement positif pour tout x. Nous justifions également que la fonction racine est dérivable en 0, car nous avons déjà montré que son intérieur est strictement positif. Donc, f est dérivable sur R.
Ensuite, nous calculons la dérivée de f en utilisant la composition et les formules de dérivation. Nous obtenons une expression pour f'(x) qui est toujours strictement positive. Donc, f est strictement croissante sur R.
Nous passons ensuite à l'étude des limites. La limite de f lorsque x tend vers plus l'infini est plus l'infini, ce que nous justifions en composant avec la limite de racine. La limite de f lorsque x tend vers moins l'infini est 0, ce que nous démontrons en utilisant la quantité conjuguée. Ainsi, nous concluons que la limite de f lorsque x tend vers plus l'infini est plus l'infini et la limite de f lorsque x tend vers moins l'infini est 0.
Enfin, nous traçons le graphique de f en utilisant des valeurs remarquables. Nous vérifions que f tend vers moins l'infini lorsque x tend vers 0 et que f tend vers plus l'infini lorsque x tend vers plus l'infini.
C'était la correction de cet exercice sur les limites. N'hésitez pas à poser vos questions dans la FAQ. Merci !
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
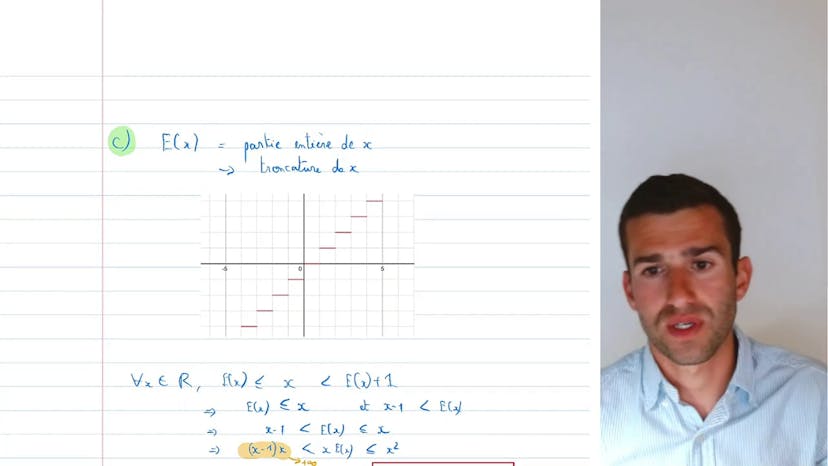
Calculs de limites complexes
Bonjour à tous, aujourd'hui nous allons étudier des exercices avancés sur les limites. Ce cours s'adresse principalement à ceux qui souhaitent se préparer pour l'année prochaine. Le premier exemple concerne les racines. Lorsque l'on rencontre des racines dans un exercice, il faut penser à utiliser la quantité conjuguée. Dans cet exemple, nous avons une forme d'indétermination avec des racines infinies. En utilisant la quantité conjuguée, nous pouvons simplifier l'expression et trouver la limite de la fonction. Dans le deuxième exemple, nous avons une expression avec des puissances. En utilisant la dérivée, nous pouvons simplifier l'expression et trouver la limite de la fonction. Le troisième exemple concerne la partie entière. En utilisant des encadrements, nous pouvons déterminer la limite de la fonction. Le quatrième exemple est similaire au premier, avec de nombreuses racines. En utilisant la quantité conjuguée et des simplifications, nous pouvons trouver la limite de la fonction. En résumé, ces exemples montrent différentes techniques pour calculer des limites dans des expressions complexes.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
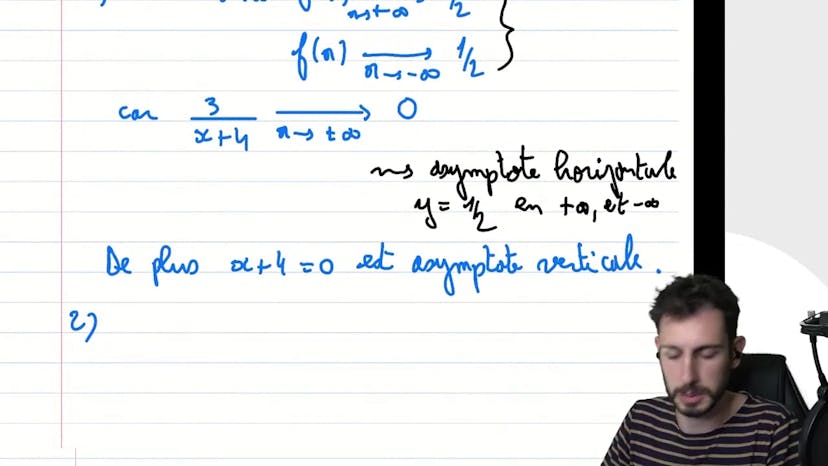
Asymptote et position relative
Ce cours est une transcription d'une vidéo qui traite de l'étude de fonctions, notamment l'étude d'asymptotes et de positions relatives. Le professeur commence par dire que l'exercice choisi est une fonction classique et qu'il souhaite rappeler les réflexes à avoir pour bien le maîtriser. Il fait remarquer que lorsqu'on voit f(x) écrit comme f2x, il faut immédiatement factoriser. Il explique que lorsqu'on étudie les limites en plus ou moins l'infini, on peut considérer que les constantes à côté de x n'ont pas d'importance. Ainsi, il simplifie rapidement la fonction en x/2x, ce qui donne 1,5. Ensuite, il aborde la réécriture des fonctions inverses, en manipulant le numerator pour que le denominator soit égal à x+4. Il sépare alors la fraction en deux et obtient une expression plus pratique à travailler. Cette écriture permet de répondre rapidement à la question 1, en identifiant les asymptotes horizontales et verticales. Ensuite, il explique que l'expression simplifiée de la fonction facilite également la réponse à la question 2, en trouvant la position relative de la fonction par rapport à l'asymptote horizontale. Il conclut en insistant sur l'importance d'intuiter et de repérer rapidement les asymptotes et les limites pour bien étudier une fonction.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
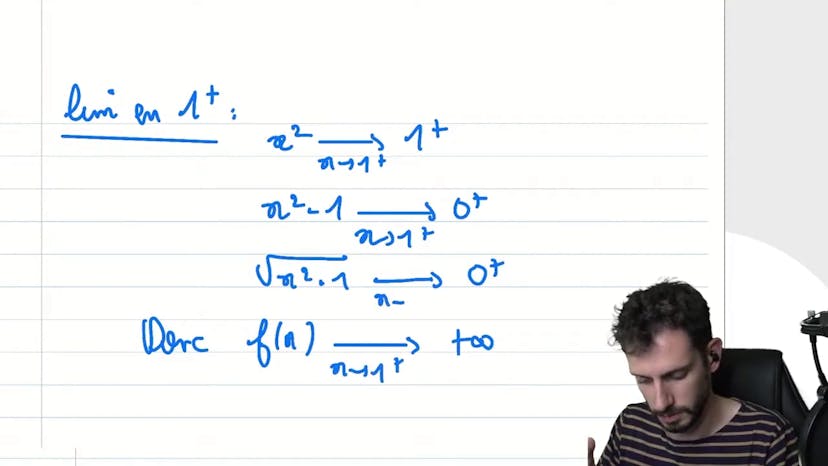
Étude TRES complète
Il est important d'écrire en français ce que vous voulez faire, car une racine n'est définie que pour des nombres positifs ou nuls sur R+. Donc, il faut que ce qu'il y a sous la racine soit positif ou nul. En gros, cela signifie que x doit être supérieur à 1 ou inférieur à -1.
En plus de cela, la fonction est définie comme un quotient, donc il faut également s'assurer que la racine de x²-1 soit différente de 0 pour éviter de diviser par 0.
Pour trouver les limites, nous pouvons utiliser deux étapes. Cependant, il est important de ne pas seulement exclure les valeurs -1 et 1, car cela ne fonctionne pas dans tous les cas. Par exemple, si nous prenons x = 0.5, nous obtenons un résultat négatif, ce qui ne fonctionne pas.
L'ensemble de définition (DF) de la fonction comprend quatre bornes. Il est important de faire attention à celles-ci.
Il est également utile de vérifier si la fonction est impaire ou paire, car cela peut réduire le travail à effectuer. Si la fonction est impaire, cela signifie que la courbe de la fonction possède un point de symétrie au point O. Par conséquent, si nous comprenons comment la fonction évolue de 0 à l'infini, nous pouvons automatiquement déduire son évolution de moins l'infini à 0.
Maintenant, passons aux calculs des limites. Nous commencerons par les limites de droite, c'est-à-dire 1 par la droite et l'infini. Lorsque x tend vers l'infini, x²-1 se rapproche de x² et la racine carrée de x² est égale à x. Ainsi, nous obtenons x/x, ce qui est environ égal à 1 lorsque x tend vers l'infini. Par symétrie, nous pouvons en déduire que lorsque x tend vers moins l'infini, la limite de la fonction sera -1.
Pour la limite en 1 par la droite, nous pouvons voir que lorsque x est légèrement supérieur à 1, x²-1 est toujours positif, ce qui signifie que nous pouvons définir la racine carrée. Cela nous donne 1/0+, ce qui est autorisé. Par symétrie, cela signifie que lorsque x tend vers moins 1 par la gauche, la limite de la fonction est également autorisée et égale à -1.
Maintenant, passons à la limite en moins l'infini. Ici, nous devons faire attention à la racine de x², car lorsque x est négatif, la racine de x² devient la valeur absolue de x. Donc, lorsque x tend vers moins l'infini, nous obtenons la valeur absolue de x, qui est légèrement supérieure à 1. Ainsi, nous pouvons dire que lorsque x tend vers moins l'infini, la racine carrée de x²-1 tend vers 0+.
En utilisant ces limites, nous pouvons conclure que la fonction a une asymptote horizontale en y = 1 pour les limites en plus l'infini, une asymptote verticale en y = -1 pour les limites en 1 par la droite, une asymptote verticale en y = -1 pour les limites en 1 par la gauche, et une asymptote verticale en y = -∞ pour les limites en moins l'infini.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Asymptote oblique
Lors de ce cours sur les asymptotes obliques, l'élève mentionne qu'il a vu ce sujet en première année et qu'il était hors programme à l'époque. Cependant, il explique que les asymptotes obliques sont souvent utilisées et qu'il est important de les maîtriser. Il effectue ensuite des calculs pour simplifier une fonction et déterminer une asymptote oblique. Il explique également comment étudier les variations de la fonction et calcule les limites aux extrêmes de l'intervalle. Enfin, il aborde la question des asymptotes verticales et horizontales, ainsi que la position relative de deux fonctions.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
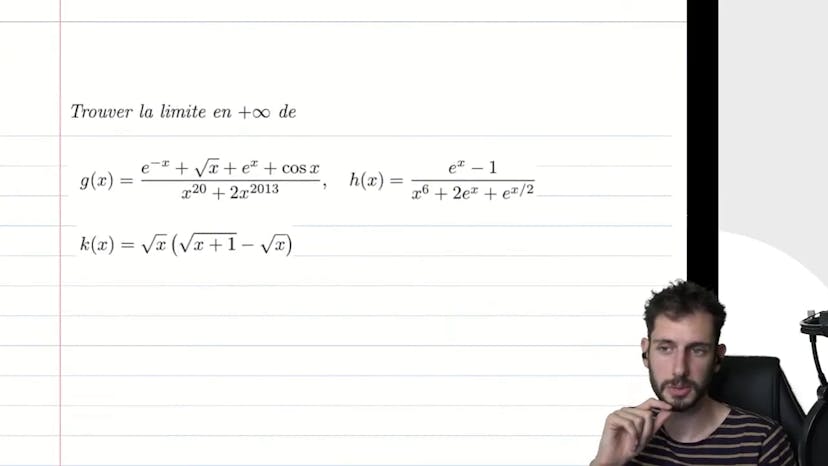
Croissance comparée plus lourde
Ce cours porte sur la croissance comparée en utilisant la fonction exponentielle. L'auteur explique notamment comment comparer la fonction exponentielle avec une autre puissance en utilisant le facteur le plus important, qui est E de x. En simplifiant cette expression, on obtient 1-E de x. Il est facile de gérer cette expression car E de x tend vers 0 lorsque x tend vers l'infini. De plus, l'exponentielle de moins x tend également vers 0 lorsque x tend vers l'infini. En utilisant ces concepts, on peut déduire que E de x sur x puissance 6 tend vers l'infini lorsque x tend vers l'infini. Cependant, il faut noter que cette tendance est inverse pour x6 sur E de x. En résumé, il est important de savoir que ces expressions tendent vers 0 lorsque x tend vers l'infini.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
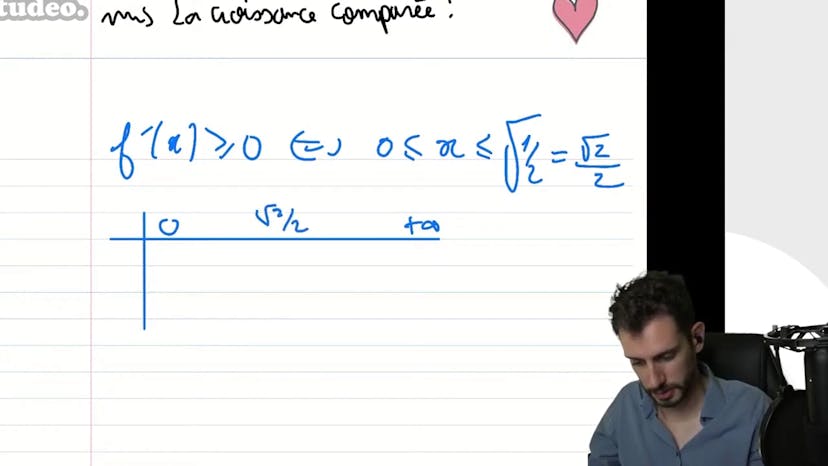
Difficile : BAC 2009
Ce cours porte sur une étude de fonction, plus précisément sur une fonction exponentielle. Le professeur explique comment trouver la limite de la fonction lorsque x tend vers l'infini et montre comment utiliser la croissance comparée pour résoudre ce problème. Ensuite, il procède à une analyse de la dérivabilité de la fonction et montre comment calculer la dérivée. En utilisant les propriétés de la dérivée, il détermine les intervalles où la fonction est positive ou nulle. Enfin, il construit un tableau de variations de la fonction et détermine le maximum de la fonction en une valeur spécifique de x. Il donne également la valeur de la fonction à cet endroit.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Exp : indéterminée en -∞
Le cours porte sur la démonstration d'une formule mathématique. L'exercice consiste à appliquer les règles des puissances pour simplifier l'expression. Ensuite, en utilisant certaines formules mathématiques connues, on peut conclure que la courbe a une asymptote horizontale à y=1. Enfin, on étudie les variations de la dérivée de la fonction et on montre qu'elle est positive ou nulle pour certains intervalles de x. On conclut en donnant les limites et asymptotes de la fonction.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Vers la SUP : Quantité conjuguée
L'exercice en question concerne le calcul d'une somme avec une limite infinie. Il est important de comprendre que c'est la variable x qui tend vers l'infini, pas le nombre d'éléments n de la somme. Pour faciliter le calcul, on peut utiliser la méthode de la quantité conjuguée, qui consiste à prendre une différence de racines. Dans ce cas, les n termes de la somme peuvent être compensés par des racines supplémentaires. En réorganisant les termes, on obtient une identité remarquable qui facilite le calcul. Finalement, en remarquant que tous les termes tendent vers zéro, on peut conclure que la somme tend vers zéro lorsque x tend vers l'infini. Il est important de ne pas se laisser distraire par des erreurs courantes, comme confondre le n avec le x, et de prendre le temps d'analyser calmement les différentes méthodes à appliquer.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
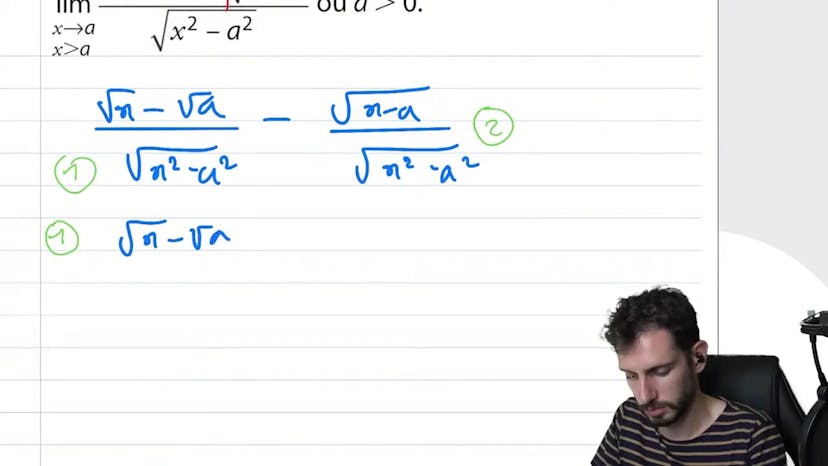
Quantité conjugée piégeuse
Le cours aborde la notion de quantité conjuguée dans le domaine des mathématiques. L'orateur explique qu'il est important de ne pas confondre une quantité conjuguée avec une simple addition ou une différence de racines. Il propose ensuite une méthode pour traiter une certaine équation en séparant la fraction en deux parties distinctes. Il utilise ensuite la quantité conjuguée pour simplifier le calcul et parvient à obtenir une expression plus simple. Il conclut en donnant le nom de la fonction étudiée et son comportement lorsque x tend vers a.
Révisions Maths lycée
Analyse Terminale
BCPST

Intro Convergence
Dans ce chapitre sur les suites, nous abordons les théorèmes de convergences. Ces théorèmes nous permettent d'analyser des suites qui semblent complexes et indomptables. Certains exemples de suites sont donnés, notamment des sinusènes. Malgré leur apparence compliquée, ces suites restent en réalité de petites valeurs. De plus, elles sont divisées par des termes très grands, tels que la racine de n ou n lui-même. Ainsi, on peut intuitivement comprendre que ces suites tendent vers zéro. Un graphique illustrant cela est présenté.
Ce chapitre est intéressant car il permet d'accéder à des théorèmes plus accessibles et compréhensibles que les définitions complexes des limites étudiées précédemment. Ces théorèmes de convergence nous permettent d'analyser des suites complexes en les comparant à des suites plus simples et classiques. On peut ainsi conclure sur des suites qui semblent intuitivement inaccessibles et compliquées.
Les principaux points abordés dans ce chapitre sont les théorèmes de comparaison et de gendarme, qui nous permettent de trouver des résultats sur les limites de suites en les comparant à d'autres suites. On étudie également les définitions de suites minorées, majorées et bornées, ainsi que le théorème de convergence monotone. Concernant les méthodes, il est important de savoir gérer des sinus de n et des moins-un puissance n, ainsi que de comprendre comment résoudre des suites homographiques.
N'hésitez pas à poser des questions et à discuter dans la FAQ. La prochaine vidéo portera sur le théorème de comparaison. À bientôt !
Révisions Maths lycée
Analyse Terminale
BCPST

Théorème de comparaison - Illustration
Le théorème de comparaison est un outil précieux en mathématiques qui permet d'économiser beaucoup d'efforts. En résumé, il dit que si une suite Vn, quel que soit son aspect peu attrayant, peut être comparée à une autre suite plus simple, et si cette dernière tend vers l'infini, alors la première tendra également vers l'infini.
Ce théorème est pratique car il permet d'éviter des démonstrations compliquées avec des epsilon et des grands A. Parfois, la suite Vn peut être de forme ingérable et difficile à manipuler. Dans ces cas-là, on utilise le théorème de comparaison en trouvant une autre suite plus simple, Un, telle que Vn soit plus grande que Un. En utilisant cette comparaison, on peut conclure que Vn tend vers l'infini.
Un exemple concret est donné pour illustrer le théorème. Si Vn est égal à l'exponentielle de la racine de n² plus 1, il est difficile de dire quelque chose de précis sur son comportement. Cependant, en comparant cette suite à la suite Un égale à la racine de n², on peut conclure que Vn est strictement plus grand que Un. Sachant que l'exponentielle est une fonction croissante, on peut alors affirmer que l'exponentielle de racine de n² plus 1 est strictement plus grande que l'exponentielle de n. Comme l'exponentielle de n est une suite géométrique qui tend vers l'infini, on peut en déduire que Vn tend également vers l'infini sans avoir à étudier le comportement détaillé de Vn.
En résumé, le théorème de comparaison permet d'économiser des efforts en trouvant une suite plus simple à laquelle on peut comparer une suite plus complexe. Si la suite simple tend vers l'infini, alors la suite complexe tendra également vers l'infini. C'est un outil puissant en mathématiques qui facilite les démonstrations et permet de conclure plus rapidement.
Révisions Maths lycée
Analyse Terminale
BCPST

Théorème de comparaison - démonstration
La démonstration de ce théorème consiste à revenir à la définition de la notion de tendre vers l'infini pour une suite. Nous partons de l'hypothèse que la limite de Un tend vers l'infini. À partir de là, nous pouvons conclure que pour tout nombre positif A, il existe un certain rang N tel que tous les éléments de la suite à partir de ce rang soient plus grands que A.
En utilisant le fait que Vn est toujours plus grand que Un, nous pouvons utiliser ce même rang N pour conclure que, pour tout N plus grand ou égal à N, Vn est plus grand ou égal à A.
Ainsi, nous avons démontré que pour tout nombre positif A, il existe un certain rang N tel que pour tout N plus grand ou égal à N, Vn est plus grand ou égal à A. Cette correspond à la définition de la divergence vers l'infini.
Cette démonstration permet de se passer des démonstrations utilisant des notions plus complexes et facilite l'utilisation du terrain de comparaison dans les exercices de ce type.
Révisions Maths lycée
Analyse Terminale
BCPST

Théorème des gendarmes
Le cours explique le théorème d'encadrement, également connu sous le nom de théorème des gendarmes, qui permet de démontrer qu'une suite converge vers une limite finie. Ce théorème stipule que si une suite UN est toujours comprise entre deux autres suites VN et WN, et que VN et WN convergent vers la même limite L, alors UN converge également vers L.
L'exemple donné dans la vidéo illustre l'utilisation du théorème d'encadrement avec une fonction sinus et ses suites correspondantes. La fonction sinus est encadrée entre -1 et 1, ce qui permet d'encadrer également les suites obtenues en évaluant la fonction sur n. Les suites encadrantes convergent vers 0, donc on peut conclure que la suite sinus n sur n converge également vers 0.
Il est précisé que toutes les situations ne sont pas aussi simples et que parfois, on dispose de moins d'informations pour conclure sur la convergence d'une suite. Cependant, une propriété est mentionnée : si deux suites un et vn sont ordonnées (un toujours plus petit que vn) et convergent, alors les limites de ces deux suites seront également ordonnées dans le même sens (la limite de vn sera plus petite que la limite de vn).
Le cours encourage les étudiants à poser des questions et à discuter entre eux dans la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Suite majorée, minorée & Th de convergence monotone
Dans cette vidéo, le concept des théorèmes de convergence est expliqué. Tout d'abord, il est expliqué ce qu'est une suite majorée et une suite minorée. Une suite est dite majorée lorsqu'elle ne dépasse jamais une certaine valeur. Par exemple, si une suite ne peut pas dépasser 3, alors elle est majorée par 3. Il est précisé qu'il peut y avoir plusieurs valeurs qui bloquent la suite par le haut. De la même manière, une suite est dite minorée lorsqu'elle ne descend jamais en dessous d'une certaine valeur. Par exemple, si une suite ne peut pas descendre en dessous de 2, alors elle est minorée par 2. Il est noté qu'il peut y avoir plusieurs valeurs qui bloquent la suite par le bas. Lorsqu'une suite est à la fois majorée et minorée, elle est dite bornée.
Des exemples de suites majorées, minorées et bornées sont donnés. Il est expliqué que le théorème de convergence monotone associe le fait d'être croissante et le fait d'être majorée, et indique que si une suite est croissante et majorée, alors elle converge vers une certaine valeur. Il est mentionné que le théorème de convergence monotone ne donne pas directement la valeur de la limite de la suite, mais permet de conclure que la suite converge.
Il est également expliqué qu'il existe des cas où une suite converge sans être croissante ou majorée, et des cas où une suite tend vers l'infini sans être décroissante ou minorée. Des contre-exemples sont donnés pour illustrer ces cas.
En conclusion, il est souligné l'importance de ne pas tirer de fausses conclusions concernant la convergence d'une suite en se basant uniquement sur le fait qu'elle tende vers une certaine valeur ou vers l'infini. Il est recommandé d'examiner attentivement les propriétés de croissance et de bornitude de la suite pour conclure sur sa convergence.
Révisions Maths lycée
Analyse Terminale
BCPST

Th convergence monotone - démo
Dans cette vidéo, nous faisons une démonstration officielle du théorème de convergence monotone dans le cas d'une suite croissante non majorée, qui tend vers l'infini. Nous commençons par donner une définition formelle de la convergence vers l'infini, qui est presque la même que celle du cas étudié. Ensuite, nous montrons que pour tout réel positif A, il existe un rang à partir duquel tous les termes de la suite sont supérieurs à A. Cela signifie que tout réel A sera finalement dépassé par la suite. Pour le prouver, nous utilisons le fait que la suite est croissante et non majorée, ce qui implique l'existence d'un rang P tel que le terme correspondant soit plus grand que A. En combinant cela avec le fait que la suite est croissante, nous pouvons montrer que pour tout rang N supérieur à P, tous les termes de la suite seront strictement supérieurs à A. Ainsi, nous avons démontré que pour tout réel fixé, la suite finit toujours par être supérieure à ce réel. Cela confirme la convergence vers l'infini. En conclusion, cette démonstration montre que dans le cas d'une suite croissante non majorée, la suite tend effectivement vers l'infini.
Révisions Maths lycée
Analyse Terminale
BCPST

Encadrer sin(n)
Dans ce cours, nous étudions deux exemples de suites utilisant les fonctions sinus et moins 1 puissance n. Dans le premier exemple, nous devons montrer que pour toute valeur de n, la suite un, égale à n plus 2 fois sin n, est supérieure à n-2. Pour ce faire, nous encadrons le terme sinus en le bornant entre -1 et 1. Ensuite, en multipliant par 2 et en ajoutant n, nous obtenons un qui est supérieur à n-2. En considérant uniquement cette partie de l'inéquation, nous montrons que un est supérieur à n-2 qui tend vers l'infini. Par comparaison, nous concluons que un tend également vers l'infini.
Dans le deuxième exemple, nous étudions la suite Vn qui vaut moins n carré moins n plus moins 1 puissance n. Encore une fois, nous encadrons le terme moins 1 puissance n en le bornant entre -1 et 1. Nous observons que le terme dominant est le terme moins n carré qui tend vers moins l'infini. En factorisant la suite, nous montrons que Vn est inférieure à une suite qui tend vers moins l'infini. Par comparaison, nous concluons que Vn tend vers moins l'infini.
En utilisant l'encadrement, nous avons démontré comment analyser des suites qui impliquent les fonctions sinus et moins 1 puissance n.
Révisions Maths lycée
Analyse Terminale
BCPST
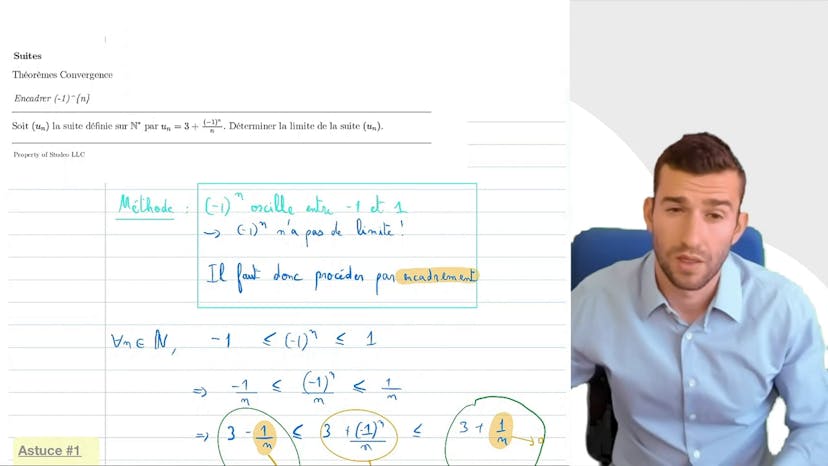
Encadrer (-1)^n
Dans ce cours, nous examinons une autre forme de suite qui nécessite une limite. Plus particulièrement, nous traitons les suites de la forme "-1 puissance n sur n". Grâce à une analyse asymptotique, nous constatons que lorsque n tend vers l'infini, cette expression tend vers 0 en raison de la division par n.
Cela signifie que la suite UN, qui est définie comme étant égale à 3 plus "-1 puissance n sur n", converge vers 3. Pour prouver cela, nous utilisons la méthode de l'encadrement. Nous commençons par encadrer "-1 puissance n" et multiplions ensuite par "1 sur n", qui est positif. En ajoutant 3, nous obtenons une inégalité de la forme 3 moins 1 sur n est inférieur à UN qui est inférieur à 3 plus 1 sur n.
En conséquence, le terme de gauche tend vers 3, tout comme le terme de droite. Par le théorème de l'encadrement, nous concluons donc que la suite UN converge vers 3. Il est également important de noter que le théorème de l'encadrement nous permet à la fois de prouver la convergence et de trouver la limite, ce qui en fait un théorème puissant.
Ainsi, grâce à l'encadrement, nous avons démontré que la suite UN tend vers 3.
Révisions Maths lycée
Analyse Terminale
BCPST

Exo TRÈS classique
Dans cette méthode, nous étudions une suite sous forme d'une fonction rationnelle de n, où le degré du numérateur est égal au degré du dénominateur. La limite de cette suite est le quotient des coefficients dominants de chacun des polynômes constituant le numérateur et le dénominateur. Cependant, au lieu de nous concentrer sur la limite elle-même, nous nous intéressons aux résultats préliminaires tels que la majoration, la croissance et la convergence, que nous déduisons à partir des théorèmes de convergence.
Dans le premier exercice, nous étudions la suite Un = (n-1)/(n+4) pour montrer qu'elle est majorée par 1. Pour cela, nous observons que le numérateur est inférieur au dénominateur s'il est inférieur à 1. Nous remarquons que -1 est inférieur à 4, puis nous ajoutons n et prenons le quotient. Comme le résultat est positif, le signe ne change pas et nous en concluons que Un est strictement inférieur à 1. Pour étudier la monotonie de la suite, nous utilisons généralement la différence Un+1 - Un. Dans certains cas, nous pouvons étudier le quotient Un+1/Un pour voir s'il est inférieur ou supérieur à 1. Cependant, il faut d'abord vérifier que Un ne s'annule jamais et ne change pas de signe. Si c'est le cas, nous pouvons étudier le quotient avec succès. Dans cet exemple, la suite est constituée de produits de quotients, ce qui permet d'utiliser cette méthode. Nous constatons que la suite ne change pas de signe, sauf en 0 où elle est négative. Cependant, cela n'a pas d'importance car nous nous intéressons à ce qui se passe à l'infini. Nous utilisons donc la méthode du quotient Un+1/Un. Nous regroupons les termes et développons l'expression pour trouver que tout est positif. Nous en déduisons que Un est strictement croissante et strictement positive, ce qui implique qu'elle converge. Cependant, la méthode ne nous permet pas de connaître la limite. Pour cela, nous appliquons la méthode du degré des polynômes en prenant les coefficients dominants, qui, dans ce cas, nous donnent une limite de 1. Il est important de noter que la limite n'est pas forcément le majorant que nous avons trouvé. Dans un autre exemple, nous avons la suite Um = (2n-2)/(n+4). En utilisant la méthode du degré des polynômes, nous concluons que la limite est de 2. Cependant, l'objectif de l'exercice est de montrer que la suite est majorée par 2, d'étudier les variations de Un et d'en déduire la convergence. Pour cela, nous utilisons une majoration successive. Nous montrons que pour tout n appartenant à N, Un est inférieur à 2. En ce qui concerne les variations de Un, nous différencions Un+1 - Un et développons l'expression. Nous observons que tout se simplifie et qu'il ne reste que 10, qui est strictement positif. Nous en concluons que Un est strictement croissante, mais nous ne savons pas vers quelle limite elle converge. Il est important de comprendre que la convergence d'une suite croissante et majorée ne signifie pas nécessairement qu'elle converge vers son majorant. En somme, il est essentiel de faire attention aux détails et de comprendre les différentes méthodes utilisées pour étudier les suites.
Révisions Maths lycée
Analyse Terminale
BCPST

Introduction Convergence
Ce cours aborde les limites de fonctions et présente plusieurs concepts importants à connaître. Il explique qu'il est nécessaire de mémoriser les tableaux de fonctions de référence, tels que la limite de 1 sur x en plus infini. Il aborde également la combinaison de limites, en examinant ce que se passe lorsque deux fonctions tendent vers quelque chose, par exemple, la limite de f plus g lorsque f tend vers 1 et g tend vers 2. Il souligne qu'il y aura des cas plus complexes, tels que lorsque f tend vers plus infini et g tend vers moins infini, et il étudiera les rapports f sur g et f fois g, en appliquant des règles spécifiques. Il présente ensuite les formes indéterminées, qui sont des cas particuliers nécessitant une attention particulière. Il aborde les théorèmes de convergence, tels que le théorème des gendarmes et le théorème de comparaison pour les limites infinies. Il introduit également la croissance comparée, en se concentrant sur l'exponentielle et les polynômes. Le cours aborde ensuite la limite de fonctions composées, expliquant que même les fonctions les plus complexes peuvent être décomposées en sous-blocs pour en analyser les limites. En résumé, il est important de maîtriser les tableaux de référence, les opérations sur les limites, les formes indéterminées et les théorèmes de convergence. Les méthodes principales à retenir sont l'utilisation du terme du plus haut degré et la méthode de la quantité conjuguée. En conclusion, en maîtrisant ces points de cours et ces méthodes, on sera prêt à aborder les diverses limites présentées dans le cours.
Révisions Maths lycée
Analyse Terminale
BCPST

Tableaux : fonctions de référence
Dans cette vidéo, le cours aborde les différentes limites et règles de combinaison des fonctions de référence en mathématiques. Voici un résumé SEO friendly de ce cours :
Le cours commence par expliquer les limites de la fonction 1/x. La limite de 1/x quand x tend vers 0 est à la fois plus et moins l'infini, et en approchant de 0 par valeur supérieure et inférieure, la fonction tend vers l'infini et moins l'infini respectivement.
Ensuite, le cours aborde les limites de la fonction x^n. Pour n impair, la fonction tend vers moins l'infini de chaque côté de l'axe des x, tandis que pour n pair, la fonction tend vers plus l'infini de chaque côté de l'axe des x.
Le cours se poursuit en expliquant les fonctions exponentielles (exp(x) et exp(-x)) et leurs limites. L'exponentielle de x tend vers plus l'infini en plus l'infini et tend vers 0 en 0, tandis que l'exponentielle de -x tend vers 0 en plus l'infini et tend vers plus l'infini en moins l'infini.
Enfin, le cours aborde les fonctions racine (sqrt(x)) et 1/sqrt(x). La racine de x tend vers 0 en plus l'infini et tend vers plus l'infini en plus l'infini. La fonction 1/sqrt(x) est similaire à 1/x, tendant vers 0 en plus l'infini et tendant vers plus l'infini en 0.
Ce résumé SEO friendly du cours explique les limites et les règles des différentes fonctions de référence, y compris les fonctions exponentielles et les fonctions racine, en fournissant une explication visuelle à travers des graphiques.
Révisions Maths lycée
Analyse Terminale
BCPST

Tableaux : combiner des limites
Ce cours porte sur les limites de somme et de produit. Les règles sont simples : lorsque deux fonctions f et g tendent vers des limites L et L' respectivement, la limite de leur somme est L + L' et la limite de leur produit est L × L'. Ensuite, si L est fini et tend vers l'infini, l'infini l'emporte toujours. Pour le produit, cela dépend du signe de L : si L est positif, la limite est l'infini inversement proportionnelle, et si L est négatif, la limite est négative inversement proportionnelle. Il est important de retenir que ces exemples ont du sens : plus l'infini plus l'infini est toujours l'infini et plus l'infini moins l'infini est moins l'infini. Cependant, il y a deux cas indéterminés, à savoir la multiplication de zéro par l'infini et l'addition de plus l'infini et moins l'infini. Une forme indéterminée signifie que les règles habituelles ne s'appliquent pas toujours et que tout peut arriver. Pour le quotient, si les fonctions f et g tendent respectivement vers les limites l et l', alors le quotient f/g tend vers l/l'. Les règles sont les suivantes : l/infini tend vers zéro, l/0 tend vers plus ou moins l'infini (selon le signe de l), et enfin, les formes indéterminées sont 0/0 et l'infini/l'infini. Il est possible d'avoir différents résultats selon les exemples donnés pour ces formes indéterminées. En conclusion, il est important de s'entraîner à utiliser des exemples simples afin de mieux comprendre ces concepts et de retenir les formes indéterminées.
Révisions Maths lycée
Analyse Terminale
BCPST

Comparaison et encadrement
Ce cours aborde deux théorèmes utilisés pour comparer des fonctions et éviter une analyse détaillée de fonctions complexes. Le premier théorème est celui de comparaison, qui établit que si deux fonctions f et g tendent vers l'infini et que g est plus grande que f, alors f va "pousser" g vers l'infini. Un exemple est donné pour illustrer ce concept.
Le deuxième théorème est celui des gendarmes, ou théorème d'encadrement. Si f et h encadrent la fonction g et que f et h tendent vers la même limite, alors g va aussi tendre vers cette limite. Une illustration graphique est donnée pour mieux comprendre ce théorème.
Ces deux théorèmes sont très utiles en pratique pour démontrer des limites finies ou infinies. Si l'on souhaite montrer une limite finie, on peut utiliser le théorème des gendarmes pour encadrer la fonction. Si l'on veut démontrer une limite infinie, on peut utiliser le théorème de comparaison pour comparer une fonction complexe à une fonction plus simple.
N'hésitez pas à poser des questions ou à faire des commentaires dans la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Croissance comparée exp et ln
Ce cours porte sur les limites de fonctions et la croissance comparée. L'idée principale est que l'exponentiel domine toujours les puissances de x. Par exemple, même si on divise l'exponentiel E2x par x puissance n, la limite de cette expression tend toujours vers l'infini.
La démonstration de cette propriété est effectuée en utilisant le théorème de comparaison. On commence par prouver que E2x sur x tend vers l'infini en comparant cette expression à x. On utilise ensuite la dérivée de la fonction f(x) = E2x - x2 sur 2 pour montrer que f'(x) est toujours positive. On construit ensuite un tableau de variation complet et concluons que f(x) est positive ou nulle.
Dans la démonstration générale pour un entier n quelconque, on utilise le résultat précédent en appliquant la propriété des puissances à l'exponentiel. On effectue un changement de variable en posant grand x égal à petit x sur n et en divisant x par n pour écrire l'exponentiel en puissance n en un seul bloc. Finalement, on conclut que lorsque x tend vers l'infini, E de x sur x puissance n tend vers l'infini.
Enfin, on démontre que lorsque x tend vers moins l'infini, E de x sur x puissance n tend vers z
Révisions Maths lycée
Analyse Terminale
BCPST

Limite des fonctions composées
La composition des fonctions est un point important dans le chapitre des limites de fonctions. L'idée est de décomposer un bloc en petits morceaux. Dans cet exemple, nous cherchons la limite de racine de 1 plus e de x lorsque x tend vers l'infini. Nous pouvons décomposer cette fonction en deux parties : la fonction 1 plus e de x et la racine de cette fonction. Si nous appelons f de x la fonction 1 plus e de x, nous pouvons dire que la limite recherchée est en fait la racine de f de x. Intuitivement, nous savons que 1 plus e de x converge vers 1 lorsque x tend vers moins l'infini, donc nous avons envie de dire que la limite recherchée est 1. Cependant, il faut démontrer cela mathématiquement en utilisant un théorème. Nous écrivons donc la limite de racine de f de x comme la limite de racine de truc lorsque truc tend vers 1, et nous montrons que cette limite est 1. En utilisant ce raisonnement, nous pouvons conclure que la limite de la composition des deux fonctions est égale à la limite de la deuxième fonction, soit 1. Ce résultat est généralisable et peut être formulé comme suit : si la limite de f de x tend vers b et la limite de g de x lorsque x tend vers b est c, alors la limite de g composé de f de x lorsque x tend vers a est égale à c.
Révisions Maths lycée
Analyse Terminale
BCPST

Forme indéterminée : utilisation du terme plus haut degré
La méthode pour déterminer les limites en plus et moins infini des polynômes et des fonctions rationnelles est de factoriser par le terme de plus haut degré, appelé terme de Claudegris. On remarque que seule cette partie du polynôme ou de la fonction rationnelle va compter pour déterminer la limite.
Pour un polynôme donné, par exemple G2x = x^4 + 4x^2 - 2x, on observe une forme indéterminée lorsque x tend vers plus ou moins infini. En factorisant par x^4, on obtient (1 + 4/x - 2/x^2). Cette expression tend vers 0, que ce soit pour x tendant vers plus ou moins infini. Donc la limite de G2x en plus et moins infini est plus l'infini.
Pour une fonction rationnelle avec un numérateur et un dénominateur (2x^2 / (1 - x)), la méthode est la même. On factorise le numérateur par x^2 (reste 2x), et le dénominateur par x (reste -1 + 1/x). L'expression (2x / (-1 + 1/x)) tend vers -1. Donc la limite de cette fonction rationnelle en plus et moins infini est plus l'infini et moins l'infini respectivement.
En résumé, la méthode consiste à factoriser par le terme de plus haut degré pour résoudre les indéterminations et déterminer les limites en plus et moins infini des polynômes et des fonctions rationnelles.
Révisions Maths lycée
Analyse Terminale
BCPST

Forme indéterminée : Méthode quantité conjuguée
La méthode de la quantité conjuguée est utilisée lorsqu'il y a des racines dans une fonction. On cherche à éliminer ces racines en multipliant la fonction par la quantité conjuguée. Par exemple, si on a une forme indéterminée lorsque x tend vers 0, on peut utiliser la quantité conjuguée pour éliminer les racines et obtenir une expression simplifiée. Cependant, cette méthode ne fonctionne pas toujours, notamment lorsque l'on a une forme indéterminée lorsque x tend vers l'infini. Dans ce cas, il est nécessaire de trouver une autre méthode de résolution. En utilisant la quantité conjuguée, on peut éliminer les racines dans la fonction et obtenir une expression simplifiée. Cela permet de lever l'indétermination et de trouver une limite plus facilement.
Révisions Maths lycée
Analyse Terminale
BCPST

Limites : la Croissance comparée
La méthode utilisée dans ce cours pour l'analyse des fonctions est la croissance comparée. La première fonction étudiée est e de x sur x. Il est démontré que cette fonction tend vers 0 lorsque x tend vers moins l'infini, et vers plus l'infini lorsque x tend vers plus l'infini.
Ensuite, une deuxième fonction h est analysée. Elle est un peu plus complexe, mais en utilisant une astuce de changement de variable, il est démontré que cette fonction tend vers 0 lorsque x tend vers moins l'infini.
La conclusion générale est que l'exponnentiel (e de x) l'emporte sur toute puissance de x. De plus, toute puissance de x l'emporte sur le logarithme népérien (ln). Donc, lors de l'analyse de fonctions, il est important de prendre en compte ces croissances comparées de référence pour faciliter la détermination des comportements asymptotiques.
Si vous avez d'autres questions, n'hésitez pas à consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Double racine
Ce cours traite de la résolution d'un exercice sur les limites d'une fonction. Tout d'abord, il est important de déterminer sur quel ensemble la fonction est définie. En l'occurrence, la fonction est définie pour tous les réels. Ensuite, il est demandé de trouver le tableau de variation de la fonction. Pour cela, il est nécessaire de prouver que la fonction est dérivable sur tout l'ensemble des réels. Pour calculer la dérivée, on utilise la décomposition de la fonction en une composition de fonctions. Après simplification, on obtient une expression de la dérivée qui est toujours positive, donc la fonction est strictement croissante sur tout l'ensemble des réels. Ensuite, on s'intéresse aux limites de la fonction. La limite en plus l'infini est prouvée en utilisant la composition de fonctions et en montrant que le terme à l'intérieur de la racine tend également vers plus l'infini. La limite en moins l'infini est montrée en utilisant une astuce avec la quantité conjuguée, qui permet de simplifier l'expression et de montrer que la limite vaut 0. Finalement, le tracé de la courbe de la fonction est réalisé en utilisant des valeurs remarquables et en observant que la fonction tend vers moins l'infini en 0 et vers plus l'infini en plus l'infini. Cette correction met également en avant l'importance de justifier les étapes de résolution et de prendre en compte les limites de la fonction lors de l'élaboration du tableau de variation.
Révisions Maths lycée
Analyse Terminale
BCPST

Calculs de limites complexes
Ce cours traite principalement de limites et présente cinq exemples complexes d'indétermination. Dans le premier exemple, il est expliqué que lorsqu'un terme avec une racine est présent, il est nécessaire de penser à l'utilisation de la quantité conjuguée. En utilisant cette méthode, il est démontré que la limite d'une expression tend vers 1/2.
Dans le deuxième exemple, l'expression x^n+1 - a^n+1 / x^n - a^n est considérée lorsque x tend vers 1. Grâce à des relations de taux d'accroissement, il est montré que cette limite converge vers (n+1) * a^n/n.
Le troisième exemple introduit la fonction de partie entière et explique comment encadrer une expression. En utilisant cette méthode, il est démontré que la limite tend vers l'infini lorsque x tend vers l'infini.
Le quatrième exemple présente une expression complexe comprenant de nombreuses racines. En utilisant la méthode de la quantité conjuguée et en décomposant l'expression en deux parties, il est démontré que la limite tend vers -1/(2 * racine de a).
Ces exemples illustrent différentes techniques pour évaluer les limites et sont destinés à ceux qui préparent des études supérieures en mathématiques.
Révisions Maths lycée
Analyse Terminale
BCPST
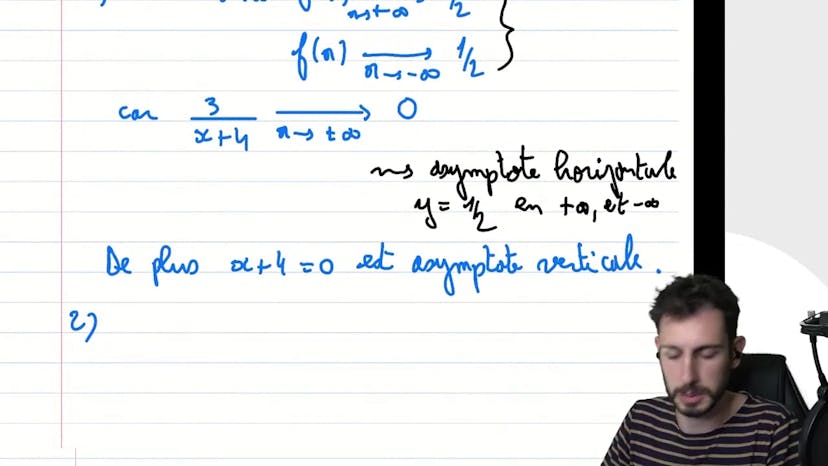
Asymptote et position relative
Résumé : Ce cours traite de l'étude d'une fonction à travers une série de questions. Le professeur rappelle certains réflexes importants pour réussir l'exercice, tels que factoriser, comprendre les limites en plus et moins l'infini, et effectuer des réécritures pour simplifier l'expression. Il souligne également l'utilité de repérer rapidement les asymptotes horizontales et verticales, ainsi que la position relative de la fonction par rapport à ces asymptotes. L'écriture utilisée dans l'exercice simplifie grandement la résolution et permet d'obtenir des résultats rapidement. L'ensemble de l'exercice souligne l'importance d'avoir des intuitions et des connaissances solides en termes de limites et d'asymptotes pour résoudre efficacement ce type de problème.
Révisions Maths lycée
Analyse Terminale
BCPST
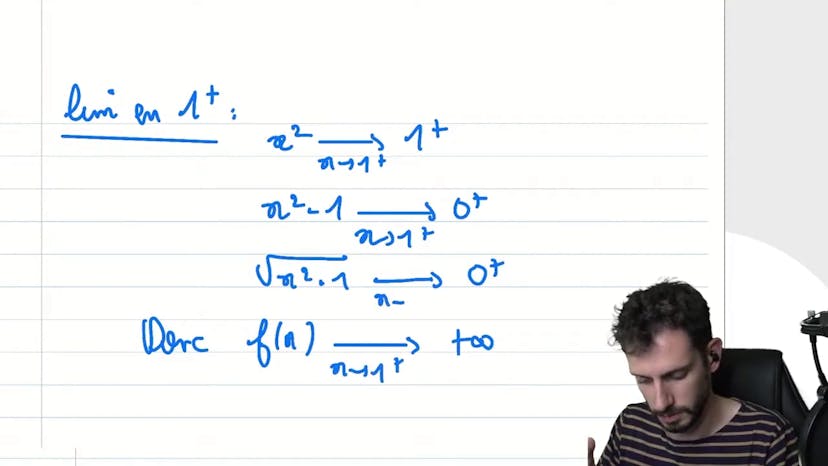
Étude TRES complète
Dans ce cours, nous étudions une fonction donnée par f(x) = √(x² - 1) / (x² - 1). Pour trouver les conditions d'existence de cette fonction, nous devons faire attention à deux choses. Tout d'abord, il faut que ce qui se trouve sous la racine soit positif ou nul, ce qui signifie que x doit être plus grand que 1 ou plus petit que -1. De plus, la fonction ne doit pas être définie pour x² - 1 = 0, c'est-à-dire lorsque x = 1 ou x = -1, car cela entraînerait une division par 0.
En utilisant ces conditions, nous pouvons déterminer les limites de la fonction. Nous remarquons tout d'abord que la fonction est impaire, ce qui nous permet de déduire les limites pour x tendant vers plus ou moins l'infini en se basant sur l'évolution de la fonction pour x près de 0. Cela nous permet de trouver que la limite de la fonction lorsque x tend vers plus ou moins l'infini est égale à 1 et -1 respectivement.
Ensuite, nous trouvons les limites pour x tendant vers 1 ou x tendant vers plus infini en utilisant les propriétés de l'imparité de la fonction. Nous trouvons que la limite de la fonction lorsque x tend vers 1+ est égale à -1 et la limite lorsque x tend vers plus infini est égale à 1. Par symétrie par rapport à l'origine, nous pouvons ensuite déduire les limites pour x tendant vers -1 et x tendant vers moins infini.
Enfin, nous examinons la présence d'asymptotes dans le graphe de la fonction. Nous trouvons une asymptote horizontale pour y = 1 lorsque x tend vers plus infini, une asymptote horizontale pour y = -1 lorsque x tend vers moins infini et une asymptote verticale pour x tendant vers -1.
En résumé, la fonction f(x) = √(x² - 1) / (x² - 1) a une limite de 1 lorsque x tend vers plus ou moins l'infini, une limite de -1 lorsque x tend vers 1 ou x tend vers moins l'infini, et présente des asymptotes horizontales pour y = 1 lorsque x tend vers plus infini et y = -1 lorsque x tend vers moins infini, ainsi qu'une asymptote verticale pour x tendant vers -1.
Révisions Maths lycée
Analyse Terminale
BCPST

Asymptote oblique
Lors de ce cours, il est question d'asymptotes obliques en mathématiques. L'enseignant mentionne qu'il a étudié ce concept en première, bien qu'il ne soit pas inclus dans le programme officiel. Il recommande cependant de connaître ce sujet car cela pourrait être abordé dans les exercices. L'enseignant fait une démonstration d'un exercice, montrant comment simplifier une fraction avec une asymptote oblique. Il explique également comment définir une fraction asymptote oblique et comment l'étudier en termes de variations et de limites. Il termine en soulignant l'importance de comprendre l'utilisation des asymptotes obliques et en expliquant comment analyser la position relative des expressions mathématiques.
Révisions Maths lycée
Analyse Terminale
BCPST
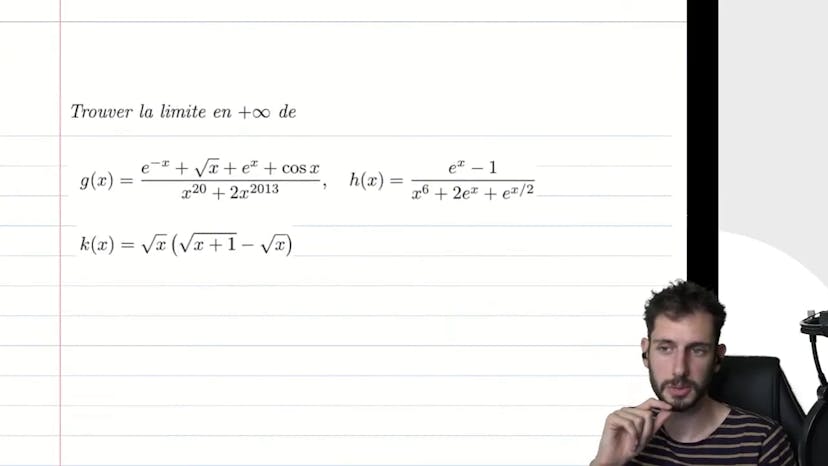
Croissance comparée plus lourde
Dans ce cours, nous étudions la croissance comparée en utilisant la comparaison entre E de x (exponentielle de x) et n'importe quelle puissance. Pour calculer cette croissance comparée, nous simplifions en utilisant le facteur qui semble le plus important, c'est-à-dire E de x. En simplifiant par E de x en haut et en bas, nous obtenons une expression idéale qui tend vers 1 - E de x. Cette expression est facile à gérer, car E de x tend vers 0. Nous examinons ensuite différentes expressions, telles que x6 sur E de x, plus 2, plus E de x, moins x sur 2, morceau par morceau. Toutes ces expressions tendent vers 0 lorsque x tend vers plus infini. De plus, nous observons que l'exponentielle de moins x tend également vers 0 lorsque x tend vers plus infini. Nous concluons en montrant que x6 sur E de x tend vers plus infini lorsque x tend vers plus infini, et l'inverse est également vrai. Pour résumer, cette étude de la croissance comparée est similaire à ce que nous avons déjà vu pour le terme dominant, avec la seule différence que cela tend vers 0.
Révisions Maths lycée
Analyse Terminale
BCPST
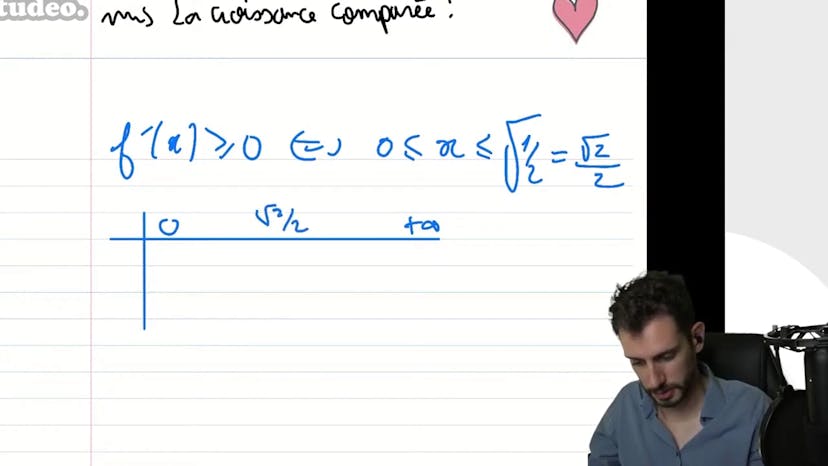
Difficile : BAC 2009
Ce cours, qui date de 2009, propose une étude de fonction complète. Tout d'abord, il faut trouver la limite de cette fonction en +∞. En utilisant la croissance comparée, on montre que l'exponentielle domine une puissance de x, ce qui permet de simplifier l'expression. Ensuite, on cherche à démontrer que la fonction admet un maximum, pour cela on calcule la dérivée et on étudie son signe. On trouve que la dérivée est positive pour x ≤ √2/2 et négative pour x > √2/2, ce qui signifie que la fonction monte puis descend. On en conclut que la fonction a un maximum en √2/2. Enfin, on calcule la valeur de ce maximum, qui est égal à √2/2 fois e^(-1.5).
Révisions Maths lycée
Analyse Terminale
BCPST

Exp : indéterminée en -∞
Ce cours traite d'un exercice classique qui permet de rappeler une limite importante en mathématiques. L'exercice consiste à étudier la fonction F(x) = x * e^(2x) / e. En utilisant les puissances, on peut simplifier l'expression et obtenir -x / e^(2x).
En étudiant la limite de cette fonction lorsque x tend vers moins l'infini, on peut déterminer que F(x) tend vers 0. De plus, on admet que F est dérivable sur R et on calcule sa dérivée, qui est x + 1 * e^(2x) - 1.
En utilisant un tableau de variations, on peut montrer que la dérivée de F est positive ou nulle lorsque x est inférieur à -1, et négative lorsque x est supérieur à -1. Ceci permet de conclure que F(x) est décroissante jusqu'à x = -1, puis croissante.
Enfin, on détermine les limites de F en moins l'infini et en plus l'infini. On trouve que la limite de F en moins l'infini est -1, tandis que la limite de F en plus l'infini est 1. On en déduit que F admet une asymptote horizontale d'équation y = 1.
En résumé, cet exercice permet de rappeler la limite classique de la fonction e^(2x) / x, de démontrer la dérivabilité de F et d'étudier ses variations. On conclut en trouvant les limites de F et en déterminant son asymptote horizontale.
Révisions Maths lycée
Analyse Terminale
BCPST

Vers la SUP : Quantité conjuguée
Ce cours porte sur une transcription d'une vidéo où il est question d'une somme avec une limite infinie. Il est important de repérer que c'est x et non n qui tend vers l'infini. Le nombre de termes reste fixe et est indiqué par n. On utilise la méthode de la quantité conjuguée pour simplifier les racines. En faisant cela, on remarque que les n termes sont compensés par d'autres termes. Ainsi, l'exercice se simplifie et on obtient une identité remarquable. En fin de compte, la réponse est que la somme tend vers zéro lorsque x tend vers l'infini. Ce cours peut sembler complexe, mais en prenant du recul et en utilisant les méthodes vues précédemment, on peut réussir à résoudre l'exercice.
Révisions Maths lycée
Analyse Terminale
BCPST
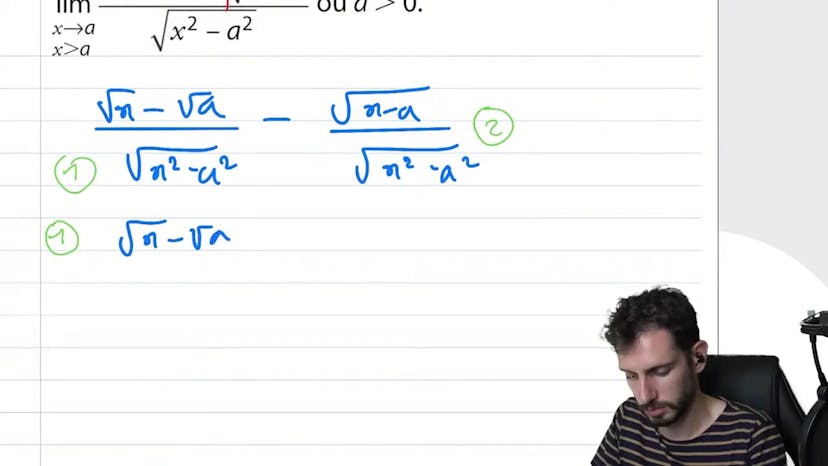
Quantité conjugée piégeuse
Dans ce cours, l'enseignant aborde la notion de quantité conjuguée et explique comment l'utiliser pour résoudre une équation. Il explique que la quantité conjuguée doit être utilisée lorsque l'on a une différence de racine. Il propose ensuite de séparer une fraction en deux parties afin de pouvoir appliquer une quantité conjuguée à chaque partie. Il décompose chaque étape de manière détaillée et explique les simplifications possibles. Finalement, il conclut en établissant une fonction f(x) basée sur les résultats précédents.
Révisions Maths lycée
Analyse Terminale
ECG

Intro Convergence
Dans ce cours, nous abordons les théorèmes de convergence des suites. Certaines suites peuvent sembler compliquées et difficiles à gérer, mais certains théorèmes nous permettent de les étudier de manière plus accessible. En utilisant des suites plus simples, nous pouvons les comparer et tirer des conclusions sur des suites en apparence complexes.
Parmi les points importants de ce cours, nous allons étudier deux théorèmes : le théorème de comparaison, qui nous permet de démontrer qu'une suite tend vers l'infini, et le théorème de gendarme, qui nous permet de montrer qu'une suite tend vers une limite finie. Nous aborderons également les notions de suites minorées, majorées et bornées, ainsi que le théorème de convergence monotone.
En ce qui concerne les méthodes, nous verrons comment travailler avec des sinus de n ou des moins-un puissance n, qui peuvent sembler compliqués de prime abord. Nous étudierons également les suites homographiques, qui sont des suites de la forme 3n+1/n+4. Ce type de suite est fréquemment rencontré et il existe des astuces pour simplifier ces expressions et gagner du temps lors des calculs.
N'hésitez pas à poser vos questions ou demander des précisions dans la FAQ. La prochaine vidéo portera sur le théorème de comparaison. À bientôt !
Révisions Maths lycée
Analyse Terminale
ECG

Théorème de comparaison - Illustration
Le théorème de comparaison est un outil puissant en mathématiques qui permet de simplifier les démonstrations. Il indique que si une suite Vn peut être comparée à une autre suite Un, et que cette dernière tend vers l'infini, alors Vn suivra le même comportement. Cela permet d'éviter des démonstrations compliquées avec des epsilon et des A.
Le théorème est utile car il permet de gérer des suites Vn qui peuvent être difficiles à manipuler. Par exemple, si Vn est de la forme exponentielle de la racine de n^2 + 1, on peut le comparer à la suite Un qui est plus simple, comme la racine de n^2. En utilisant le fait que l'exponentielle est croissante, on peut conclure que Vn sera plus grand que E^n, qui est une suite géométrique qui tend vers l'infini. Ainsi, en utilisant le théorème de comparaison, on peut dire que Vn tend également vers l'infini, sans avoir à étudier en détail la forme de Vn.
En résumé, le théorème de comparaison en mathématiques permet de simplifier les démonstrations en comparant une suite complexe à une autre plus simple. Cela permet d'éviter des calculs laborieux et d'obtenir des résultats plus rapidement.
Révisions Maths lycée
Analyse Terminale
ECG

Théorème de comparaison - démonstration
Le cours explique une démonstration concernant la divergence d'une suite tendant vers l'infini. Pour démontrer cela, il est nécessaire de revenir à la définition. On traduit la limite de la suite U n tendant vers l'infini en disant que si la limite de U n est égale à l'infini, alors quelque chose se produit. Plus précisément, pour tout A positif, il existe un certain rang N à partir duquel tous les termes de la suite U n sont plus grands que A. Ce raisonnement est valable pour tous les N plus grands ou égaux à ce rang N. Ainsi, on peut conclure que pour tout A positif, il existe un rang N à partir duquel tous les termes de la suite V n (qui sont plus grands ou égaux à U n) sont aussi plus grands ou égaux à A. Cette conclusion correspond à la définition de la divergence vers l'infini. Cette démonstration permet d'éviter l'utilisation de termes tels que epsilon ou grand A dans les exercices utilisant le terrain de comparaison.
Révisions Maths lycée
Analyse Terminale
ECG

Théorème des gendarmes
Le théorème d'encadrement, aussi appelé théorème des gendarmes, permet de montrer qu'une suite converge vers un réel fini en la comparant à deux autres suites qui convergent vers la même limite. Si une suite UN est "prise en sandwich" entre deux autres suites VN et WN, c'est-à-dire que UN est plus grande que VN et plus petite que WN, et que VN et WN convergent tous les deux vers la même limite L, alors UN converge également vers L. Ce théorème permet d'éviter les définitions formelles d'ε et d'A et offre une méthode pratique pour prouver des résultats sur les suites.
Pour illustrer ce théorème, on peut prendre l'exemple de la suite sinus n sur n. Cette suite est difficile à gérer, mais on peut l'encadrer entre les suites 1 sur n et -1 sur n, qui convergent toutes les deux vers 0. En appliquant le théorème des gendarmes, on peut conclure que la suite sinus n sur n converge également vers 0.
Il faut cependant noter que toutes les situations ne sont pas aussi simples et il peut arriver qu'on ait moins d'informations pour prouver la convergence d'une suite. Néanmoins, une propriété importante à retenir est que si deux suites un et vn sont ordonnées, c'est-à-dire que un est toujours plus petit que vn, et que ces deux suites convergent, alors leurs limites seront également ordonnées dans le même sens.
En résumé, le théorème d'encadrement, ou théorème des gendarmes, est une méthode pratique pour prouver la convergence d'une suite vers un réel fini en la comparant à deux autres suites convergentes. Il permet d'éviter les définitions formelles et offre des résultats intuitifs.
Révisions Maths lycée
Analyse Terminale
ECG

Suite majorée, minorée & Th de convergence monotone
Le cours concerne les théorèmes de convergence en mathématiques. La première définition donnée est celle de la notion de suite majorée, c'est-à-dire lorsque celle-ci est bloquée par une certaine valeur et toutes les valeurs supérieures. Ensuite, la notion de suite minorée est expliquée, qui représente le fait que la suite ne peut pas descendre en dessous d'une certaine valeur. Lorsqu'une suite est à la fois majorée et minorée, on dit qu'elle est bornée. Ensuite, des exemples de suites bornées sont donnés, comme la suite 2-1/n qui ne dépasse jamais 2, la suite 1/n qui ne descendra jamais en dessous de 0, et la suite sin(n) qui oscille entre 1 et -1.
Ensuite, le théorème de convergence monotone est présenté. Il établit que si une suite est croissante et majorée, alors elle converge. Cependant, le théorème ne fournit pas la valeur limite vers laquelle la suite converge.
Il est également expliqué que la réciproque du théorème de convergence monotone est fausse, c'est-à-dire que ce n'est pas parce qu'une suite converge qu'elle est forcément croissante et majorée, ou décroissante et minorée. Des contre-exemples sont donnés, notamment la suite sin(n) qui converge vers 0 mais oscille de manière chaotique.
En conclusion, il est souligné l'importance de bien comprendre ces concepts et de ne pas se laisser piéger par des fausses idées.
Révisions Maths lycée
Analyse Terminale
ECG

Th convergence monotone - démo
Le théorème de convergence monotone démontre que dans le cas d'une suite croissante non majorée, celle-ci tend vers l'infini. Pour démontrer cela, on commence par se donner un A positif strict et on va montrer qu'à partir d'un certain rang, la suite sera toujours au-dessus de A. Comme la suite UN n'est pas majorée, il existe donc un rang P à partir duquel UP sera plus grand que A. De plus, étant donné que la suite est croissante, pour tout N au-dessus de P, UN sera toujours plus grand que UP. Ainsi, à partir de P, pour tout N au-dessus de P, UN sera plus grand strict que A. Cela montre que la suite finit toujours par être au-dessus de tout A fixé, ce qui signifie qu'elle tend vers l'infini.
Révisions Maths lycée
Analyse Terminale
ECG

Encadrer sin(n)
Ce cours présente deux exemples d'application des théorèmes de convergence pour les fonctions sinus et moins 1 puissance n (exponentiation). Dans le premier exemple, nous étudions la suite un, définie comme n plus 2 fois sinus n. L'objectif est de montrer que pour tout n, un est supérieur à n-2. Pour cela, nous utilisons l'encadrement du sinus entre -1 et 1, et nous construisons la suite un en multipliant par 2 et en ajoutant n. Ainsi, nous obtenons un qui est supérieur à n-2. En utilisant la comparaison avec une suite qui tend vers l'infini, nous concluons que la suite un tend également vers l'infini. Dans le deuxième exemple, nous examinons la suite Vn, définie comme moins n carré moins n plus moins 1 puissance n. Puisque nous avons une puissance négative et alternante, nous utilisons à nouveau l'encadrement pour montrer que Vn est inférieur à une suite qui tend vers moins l'infini. En factorisant et en simplifiant les termes de plus haut degré, nous concluons que la suite Vn tend également vers moins l'infini. Ainsi, ces deux exemples illustrent comment utiliser l'encadrement pour traiter des suites impliquant sinus ou moins 1 puissance n.
Révisions Maths lycée
Analyse Terminale
ECG
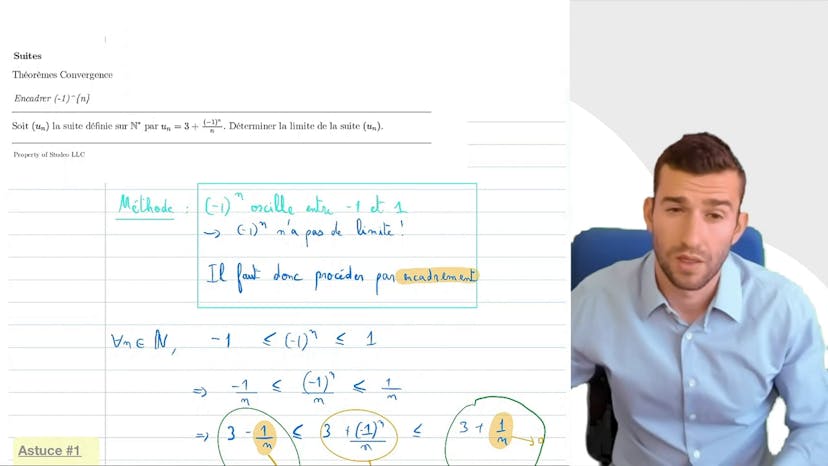
Encadrer (-1)^n
Dans ce cours, nous étudions un type particulier de suites nécessitant une borne supérieure. Ces suites sont de la forme "-1 puissance n sur n". Grâce à une analyse asymptotique, nous pouvons constater que lorsque n tend vers l'infini, le terme UN de la suite tend vers 3. Pour prouver cela, nous utilisons la méthode de l'encadrement. Nous partons de l'encadrement de "-1 puissance n", puis nous multiplions par un sur n, qui étant positif, ne change pas le sens des inégalités que nous utilisons. En ajoutant également 3, nous obtenons ainsi une double inégalité avec le terme UN. D'après le théorème d'encadrement, puisque les termes à gauche et à droite tendent tous deux vers 3, nous pouvons conclure que la suite UN tend effectivement vers 3. Il est important de rappeler que le théorème d'encadrement permet non seulement de prouver la convergence d'une suite, mais aussi de trouver sa limite, ce qui en fait un théorème très puissant. Ainsi, par l'encadrement, nous avons démontré que la suite UN tend vers 3.
Révisions Maths lycée
Analyse Terminale
ECG

Exo TRÈS classique
Dans cette méthode, nous étudions une suite qui est une fonction rationnelle de n, où le degré du numérateur est égal au degré du dénominateur. La limite de cette suite est donnée par le quotient des coefficients dominants de ces polynômes. Cependant, nous ne nous intéressons pas directement à la limite, mais plutôt aux résultats préliminaires tels que la majoration, la croissance et la convergence.
Dans le premier exercice, nous devons montrer que la suite Un = (n-1)/(n+4) est majorée par 1. Pour cela, nous constatons que si le numérateur est inférieur à 1, alors le numérateur est inférieur au dénominateur. En partant de -1, nous remarquons que -1 est inférieur à 4. En ajoutant n et en effectuant le quotient, nous obtenons Un < 1.
Ensuite, pour étudier la monotonie de la suite, nous utilisons souvent la différence Un+1 - Un. Dans certains cas, nous pouvons également étudier le quotient Un+1 / Un. Cependant, certaines conditions doivent être vérifiées, comme le fait que Un ne s'annule jamais et ne change pas de signe. Si ces conditions sont remplies, le quotient peut être étudié.
Concernant la convergence, nous pouvons utiliser la méthode du quotient Un+1 / Un. En développant cette expression, nous obtenons une différence avec deux quotients. En regroupant tout au même numérateur, nous pouvons nous intéresser au signe du numérateur. Si le numérateur est positif, nous pouvons conclure que la suite Un est strictement croissante et positive. Cela implique qu'elle est croissante et majorée, donc convergente.
Cependant, il est important de noter que la limite n'est pas nécessairement le majorant trouvé. La limite peut être différente et il est donc essentiel de faire attention à cela. En utilisant les coefficients dominants des polynômes, nous pouvons facilement trouver la limite de la suite s'il s'agit d'une fonction rationnelle.
Dans l'exemple avec Un = (2n-2) / (n+4), nous montrons d'abord que la suite est majorée par 2. En utilisant la méthode de majoration successive, nous pouvons prouver que pour tout n appartenant à N, Un < 2. Ensuite, nous étudions les variations de la suite en calculant la différence Un+1 - Un. Après développement, nous obtenons un résultat strictement positif, ce qui signifie que la suite Un est strictement croissante. En utilisant le théorème de convergence, nous pouvons conclure que la suite Un converge, mais sans connaître sa limite exacte.
Il est important de noter que la méthode de la différence Un+1 - Un permet d'étudier les variations et la convergence de la suite, alors que la méthode du quotient Un+1 / Un permet de trouver directement la limite de la suite si elle est une fonction rationnelle.
Révisions Maths lycée
Analyse Terminale
ECG

Introduction Convergence
Dans ce nouveau sous-chapitre sur les limites de fonctions, nous allons aborder des sujets plus concrets que les définitions précédentes. Nous devrons connaître quelques tableaux de référence par cœur, par exemple la limite de 1/x quand x tend vers l'infini. Nous étudierons également comment combiner différentes limites, par exemple si f tend vers 1 et g tend vers 2, alors f+g tend vers 3. Cependant, il y aura aussi des cas plus complexes, par exemple lorsque f tend vers l'infini et g tend vers moins l'infini. Dans ces situations, nous examinerons le rapport f/g et le produit f*g, et nous devrons appliquer des règles spécifiques. Il y aura certaines règles essentielles à connaître en permanence, ainsi que quatre formes indéterminées pour lesquelles il n'y a pas de règles prédéfinies. Cela peut poser problème et il faudra faire attention. Ensuite, nous étudierons des théorèmes de convergence similaires à ceux des suites. Nous verrons le théorème du gendarme, où deux fonctions encadrent une troisième fonction pour l'amener vers la même limite. Nous examinerons également le théorème de comparaison pour les limites infinies. En outre, nous étudierons la croissance comparée, qui se concentrera principalement sur les fonctions exponentielles et les polynômes. Nous apprendrons également comment gérer les fonctions plus complexes en les décomposant en sous-blocs. En résumé, il est important de connaître les tableaux de référence, les opérations sur les limites, les formes indéterminées, ainsi que les théorèmes de comparaison, du gendarme, de croissance comparée et des limites des fonctions composées. On nous présentera deux méthodes essentielles pour gérer les formes indéterminées : l'utilisation du terme de plus haut degré et la méthode de quantité conjuguée. Si nous maîtrisons ces concepts, nous serons prêts à aborder tous types de limites. N'hésitez pas à poser des questions dans la FAQ si vous en avez, et à consulter les discussions existantes sur les sujets qui vous intéressent. À bientôt !
Révisions Maths lycée
Analyse Terminale
ECG

Tableaux : fonctions de référence
Ce cours transcrit une vidéo qui fait le point sur les fonctions de référence et leurs limites en mathématiques. Il aborde également les règles de combinaison pour les différentes fonctions.
Tout d'abord, il explique que la limite de 1/x est infinie lorsque x tend vers plus ou moins l'infini, et que la limite de 1/x est 0 lorsque x tend vers 0. Il utilise des graphiques pour illustrer ces concepts.
Ensuite, il observe les limites de x^n, où n est un nombre entier. Les fonctions x^n tendent rapidement vers plus l'infini lorsque x devient de plus en plus grand. Pour les nombres impairs, les fonctions x^n sautent d'un côté à l'autre de l'axe des abscisses.
Le cours aborde ensuite les limites des fonctions exponentielles et des racines. Les fonctions exponentielles tendent vers l'infini lorsque x tend vers l'infini, et vers 0 lorsque x tend vers moins l'infini. Les fonctions racines, quant à elles, ont des limites spécifiques. La racine de x tend vers 0 lorsque x tend vers 0, et 1/sqrt(x) tend vers 0 lorsque x tend vers l'infini.
Le cours souligne l'importance de bien comprendre le signe des expressions dans les limites et de les combiner correctement. Enfin, il conseille de faire des fiches avec des dessins pour mieux mémoriser ces concepts.
Note : pour optimiser le résumé en termes de référencement SEO, il faudrait prendre en compte les mots-clés importants tels que "fonctions de référence", "limites", "règles de combinaison", "graphiques", "fonctions exponentielles", "racines", "interprétation graphique", "intuition", etc.
Révisions Maths lycée
Analyse Terminale
ECG

Tableaux : combiner des limites
Ce cours porte sur les limites des fonctions. Les règles sont les suivantes :
- Lorsque deux fonctions, f et g, tendent chacune vers une limite L et L', respectivement, la limite de la somme f + g est L + L' et la limite du produit f * g est L * L'.
- Lorsque l'une des limites est finie et l'autre est infinie, l'infini l'emporte. Si L est positif, le résultat est l'infini positif. Si L est négatif, le résultat est l'infini négatif.
- Pour le produit, le résultat dépend du signe de L. Si L est positif, le produit tend vers l'infini négatif. Si L est négatif, le produit tend vers l'infini positif.
- Il existe des cas indéterminés, où il est impossible de déterminer la limite. Ces cas incluent la multiplication de zéro par l'infini et l'addition de l'infini positif et de l'infini négatif.
- Une forme indéterminée signifie qu'il n'y a pas de règle définie applicable tout le temps. Différents résultats peuvent être obtenus en fonction des fonctions utilisées.
- Le quotient de deux fonctions, f/g, tend vers L/L' si les deux tendent respectivement vers L et L'. Si L tend vers l'infini, le quotient tend vers zéro. Si L tend vers zéro, le quotient tend vers l'infini (positif ou négatif).
- Il y a également des formes indéterminées pour les quotients, notamment 0/0 et l'infini/infini. Ces formes indéterminées peuvent avoir différents résultats en fonction des fonctions utilisées.
Il est important de retenir les formes indéterminées et de pratiquer des exemples simples pour mieux comprendre les concepts.
Révisions Maths lycée
Analyse Terminale
ECG

Comparaison et encadrement
Dans ce cours, nous étudions deux théorèmes de comparaison pour les fonctions. Le premier théorème de comparaison stipule que si deux fonctions f et g vérifient f tend vers plus l'infini et g est plus grande que f, alors f va également tendre vers plus l'infini. En d'autres termes, si f pousse vers l'infini, g va suivre cette tendance.
Pour illustrer cela, nous prenons l'exemple de deux fonctions : f(x) = x²/4 + x et g(x) = x²/32 + x. En tracant les graphiques de ces fonctions, nous voyons que g est toujours au-dessus de f. Ainsi, si f tend vers plus l'infini, cela signifie que g va également tendre vers plus l'infini, car g est "poussée" par f.
Le second théorème, appelé le théorème des gendarmes ou d'encadrement, affirme que si deux fonctions, f et h, encadrent une fonction g et que f et h tendent vers la même limite, alors g tendra également vers cette limite. Pour illustrer cela, nous prenons l'exemple de trois fonctions : f(x) = 3 + 1/x, g(x) = 3 + 5/x, et h(x) = 3 - 5/x. Nous voyons que g est comprise entre f et h. De plus, si f et h tendent vers 3, alors g tendra également vers 3.
Ces théorèmes sont utiles pour comparer et analyser des fonctions sans avoir à étudier en détail des aspects complexes. Ils permettent de donner des indications sur le comportement d'une fonction en se basant sur des fonctions plus simples. Cela peut être très pratique pour résoudre des exercices qui demandent de déterminer des limites ou des tendances de fonctions.
N'hésitez pas à me poser des questions ou à laisser des commentaires dans la FAQ si vous avez besoin de plus d'explications. Bonne journée ou soirée à vous.
Révisions Maths lycée
Analyse Terminale
ECG

Croissance comparée exp et ln
Dans ce cours, on aborde le sujet de la croissance comparée en mathématiques. On explique que la croissance exponentielle domine complètement les puissances de x. Peu importe la puissance de x, l'exponentiel sera toujours supérieur et tendra vers l'infini. On peut le voir graphiquement, où l'exponentiel monte très rapidement et les puissances de x sont rapidement dépassées. On démontre la formule de croissance comparée en utilisant le théorème de comparaison, en comparant l'exponentiel sur x à une fonction simple qui tend vers l'infini. On fait également usage du changement de variable pour simplifier les calculs. En utilisant ces techniques, on démontre que lorsque x tend vers l'infini, l'exponentiel sur x tend également vers l'infini. On utilise ensuite la même méthode pour montrer que lorsque x tend vers moins l'infini, l'exponentiel sur x tend vers zéro. Ces démonstrations peuvent être utiles dans d'autres contextes mathématiques et il est important de comprendre et de savoir utiliser ces méthodes.
Révisions Maths lycée
Analyse Terminale
ECG

Limite des fonctions composées
La composition de fonctions est un concept important dans les limites de fonctions en mathématiques. Pour comprendre cela, prenons l'exemple de la fonction racine de (1 + e^x). On peut décomposer cette fonction en deux parties : d'abord, la fonction f(x) = 1 + e^x, puis la racine de f(x). Nous cherchons donc à trouver la limite de la fonction racine de f(x) lorsque x tend vers l'infini. Intuitivement, nous savons que f(x) converge vers 1 lorsque x tend vers moins l'infini. Nous voulons donc dire que la limite de la fonction racine de f(x) est également 1. Cependant, il est important de démontrer cette affirmation à l'aide d'un théorème mathématique. Ce théorème nous permet d'établir une relation entre la limite de f(x) et celle de la fonction racine, permettant ainsi de conclure que la limite de la composition des deux fonctions est 1. En résumé, le théorème nous autorise à faire cette composition en deux étapes et confirme notre intuition initiale.
Révisions Maths lycée
Analyse Terminale
ECG

Forme indéterminée : utilisation du terme plus haut degré
La méthode pour déterminer les limites des polynômes et des fonctions rationnelles est très simple. On factorise par le terme de plus haut degré, appelé terme de Claudegris. Par exemple, pour un polynôme G2x, on factorise par x4, ce qui donne 1+4/x^2-2/x^3. Peu importe si x tend vers plus infini ou moins infini, la limite sera plus infini. Pour une fonction rationnelle, on factorise le numérateur et le dénominateur par le terme de Claudegris. Par exemple, pour h2x = (2x^2)/(1-x), on factorise le dénominateur par x, ce qui donne (2x)/(1+1/x). En faisant attention aux signes, on trouve que la limite sera moins infini en moins infini, et plus infini en plus infini. En résumé, il suffit de factoriser par le terme de plus haut degré pour résoudre les indéterminations des polynômes et des fonctions rationnelles. Il est important de maîtriser cette méthode car elle fonctionne à tous les coups.
Révisions Maths lycée
Analyse Terminale
ECG

Forme indéterminée : Méthode quantité conjuguée
La méthode de la quantité conjuguée est utilisée lorsque nous avons des racines dans une fonction et que nous souhaitons éliminer ces racines. La quantité conjuguée est multipliée en haut et en bas de la fonction pour supprimer les racines.
Dans l'exemple donné, la fonction présente une forme indéterminée lorsque x tend vers zéro. Cependant, lorsque x tend vers zéro depuis la droite (0+), la fonction est bien définie.
Pour traiter la limite lorsque x tend vers l'infini, la quantité conjuguée est utilisée car la fonction présente une forme indéterminée. En multipliant la fonction par sa quantité conjuguée, les racines du dénominateur disparaissent mais apparaissent dans le numérateur. Cependant, en effectuant cette manipulation, le signe négatif devient positif, éliminant ainsi la forme indéterminée.
Dans l'exemple donné, après avoir utilisé la quantité conjuguée, la fonction se réduit à racine de x plus 1 plus racine de x, ce qui n'est plus une forme indéterminée. La limite de la fonction lorsque x tend vers l'infini est donc plus l'infini.
En résumé, la méthode de la quantité conjuguée est utilisée pour éliminer les racines dans une fonction et résoudre des formes indéterminées. Cette méthode est particulièrement utile lorsque nous avons des différences de racines dans une fonction.
Révisions Maths lycée
Analyse Terminale
ECG

Limites : la Croissance comparée
La croissance comparée est une méthode utile en mathématiques pour étudier le comportement des fonctions. Dans ce cours, nous avons analysé deux fonctions.
La première fonction est f(x) = e^x/x. Pour x tendant vers l'infini, cette fonction tend également vers l'infini. En utilisant la croissance comparée, nous constatons que e^x domine toute puissance de x, même si cette dernière est très grande. Ainsi, f(x) tend vers l'infini.
La deuxième fonction est h(x) = x^4 / e^2x. Lorsque x tend vers moins l'infini, nous observons que x^4 tend vers moins l'infini, tandis que e^2x reste constant. Puisque le terme x^4 est plus grand que le terme e^2x, selon la croissance comparée, h(x) tend vers moins l'infini.
En résumé, la croissance comparée nous permet de déterminer le comportement des fonctions. L'exponentielle (e^x) l'emporte sur toute puissance de x, tandis que le logarithme (ln) est inférieur à toute puissance de x. N'hésitez pas à consulter la FAQ si vous avez des questions supplémentaires.
Révisions Maths lycée
Analyse Terminale
ECG

Double racine
Dans ce cours, il est question de la fonction f(x) = √(x + √(1 + x^2)). Tout d'abord, il est demandé de montrer que f est définie sur R, l'ensemble des réels. Pour cela, il faut vérifier que les racines dans la fonction sont bien définies. On peut constater que pour x supérieur à 0, il n'y a pas de problème car tous les termes sont positifs. En revanche, pour x inférieur à 0, il faut comparer les deux termes de la seconde racine. On peut voir que √(1 + x^2) est supérieur à |x|, donc la racine est définie pour toute valeur de x appartenant à R.
Ensuite, la dérivabilité de f sur R est abordée. On rappelle que la fonction racine n'est pas dérivable en 0. Ici, on décompose la fonction dans la forme f(x) = x + √(1 + x^2) et on vérifie que les termes à l'intérieur des racines sont strictement positifs, ce qui nous permet de dire que f est dérivable sur R. On calcule ensuite la dérivée de f en utilisant la formule de dérivation de la fonction racine. On obtient ainsi f'(x) = (√(1 + x^2) + x)/(√(1 + x^2)). On constate que les termes numérateur et dénominateur sont tous deux strictement positifs, ce qui indique que f est strictement croissante sur R.
Ensuite, les limites de f en moins l'infini et plus l'infini sont étudiées. Pour la limite en plus l'infini, on observe que les deux racines tendent vers plus l'infini et donc f tend également vers plus l'infini. Pour la limite en moins l'infini, on utilise la quantité conjuguée pour simplifier l'expression de f et on obtient que f tend vers 0. Enfin, le tracé de la courbe de f est abordé, en notant que la fonction tend vers moins l'infini en 0 et vers plus l'infini en plus l'infini.
Révisions Maths lycée
Analyse Terminale
ECG

Calculs de limites complexes
Dans ce cours, l'enseignant aborde plusieurs exemples complexes de limites. Il commence par expliquer l'utilisation de la quantité conjuguée pour gérer les racines dans une expression. Dans le premier exemple, il factorise l'expression par la racine de x pour la simplifier et trouve que la limite tend vers 1/2.
Dans le deuxième exemple, il utilise la dérivée pour simplifier l'expression et trouve que la limite est (n+1)/(n*a).
Le troisième exemple concerne la partie entière d'un nombre. L'enseignant explique comment encadrer la partie entière pour obtenir un résultat. La limite tend finalement vers l'infini.
Le quatrième exemple est constitué de nombreuses racines. L'enseignant utilise à nouveau la quantité conjuguée pour simplifier l'expression et trouve que la limite tend vers -1/(2*racine de a).
Dans l'ensemble, ce cours aborde des exemples complexes de limites et donne des astuces pour les simplifier.
Révisions Maths lycée
Analyse Terminale
ECG
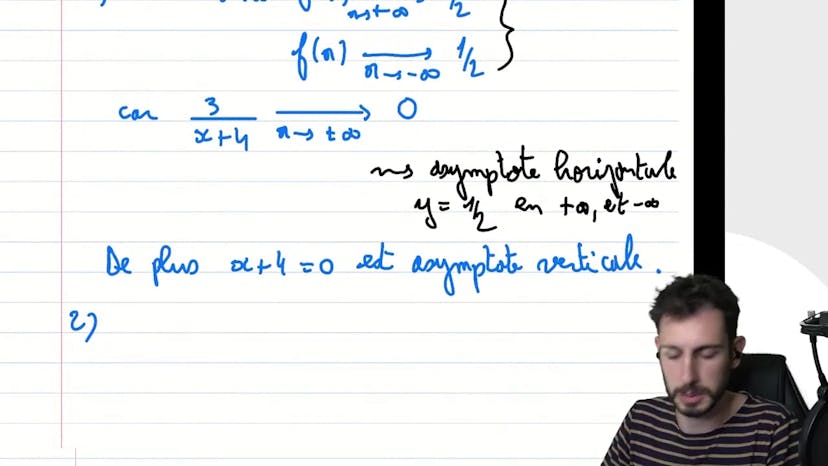
Asymptote et position relative
Ce cours est une transcription d'une vidéo qui concerne l'étude de fonctions, plus précisément l'étude de positions relatives et d'asymptotes. Le professeur explique que la question 2 de l'exercice est importante et permet de rappeler certains réflexes indispensables pour réussir l'exercice.
Tout d'abord, il faut factoriser dès que possible. Ensuite, le professeur explique qu'il est possible de simplifier les limites à l'infini en considérant que les valeurs deviennent énormes, ce qui permet d'obtenir rapidement la réponse.
Ensuite, le professeur parle de réécriture. Il explique qu'il est possible de réécrire une fonction homographique sous la forme d'une fonction inverse en séparant le numérateur et le dénominateur. Cette réécriture permet de mettre en évidence les éléments clés du comportement asymptotique de la fonction.
Il explique ensuite comment trouver les asymptotes de la fonction. Pour cela, il utilise l'écriture obtenue précédemment et déduit rapidement les asymptotes horizontales et verticales.
Ensuite, il aborde la question de la position relative de la fonction par rapport à l'asymptote horizontale. Il explique qu'il faut faire la différence entre l'expression de la fonction et celle de l'asymptote. Grâce à l'écriture obtenue précédemment, il est facile de répondre à cette question.
Le professeur conclut en soulignant l'importance de savoir trouver rapidement les asymptotes et de repérer les limites pour réussir ces types d'exercices. Il explique qu'il est essentiel de développer cette intuition pour simplifier les calculs et obtenir des réponses plus rapidement.
Révisions Maths lycée
Analyse Terminale
ECG
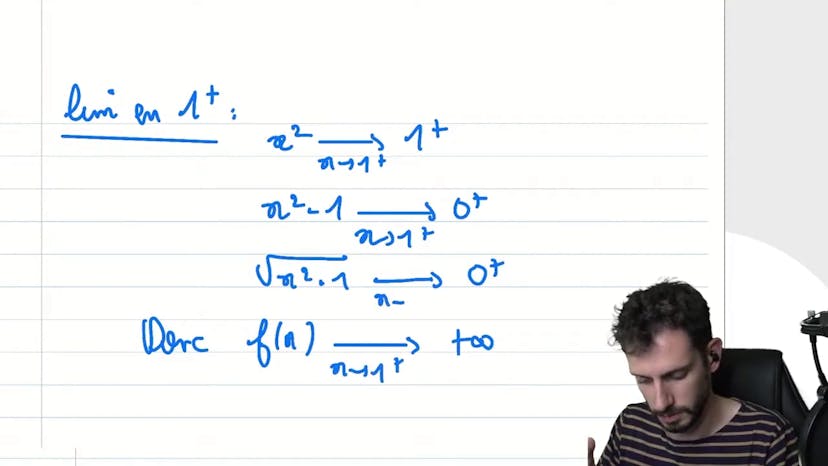
Étude TRES complète
Ce cours porte sur le calcul des limites d'une fonction. L'objectif est de déterminer les valeurs vers lesquelles la fonction tend lorsque la variable x se rapproche de certaines valeurs.
Pour cela, plusieurs conditions doivent être vérifiées. Tout d'abord, la racine carrée de x²-1 doit être différente de 0, afin d'éviter une division par 0. De plus, la fonction doit être définie pour des valeurs de x supérieures à 1 ou inférieures à -1.
Il est également important de vérifier si la fonction est paire ou impaire. Si elle est impaire, cela signifie que son évolution pour des valeurs positives de x sera symétrique par rapport à l'axe des ordonnées. Ainsi, si la fonction tend vers une valeur en plus l'infini, elle tendra vers son opposé en moins l'infini.
En utilisant ces conditions, on peut déterminer les limites de la fonction pour différentes valeurs de x, telles que plus l'infini, moins l'infini et 1 plus. Par exemple, en plus l'infini, la fonction tend vers 1, tandis qu'en moins l'infini, elle tend vers moins 1.
En résumé, ce cours aborde le calcul des limites d'une fonction en utilisant des conditions spécifiques telles que la positivité de la racine carrée et la parité de la fonction. Il permet de déterminer les valeurs vers lesquelles une fonction tend lorsque la variable x se rapproche de certaines valeurs.
Révisions Maths lycée
Analyse Terminale
ECG

Asymptote oblique
L'asymptote oblique a été étudiée en première, bien qu'elle ne faisait pas partie du programme. Cependant, il est recommandé de connaître son concept car il peut être utilisé dans des exercices. Une asymptote oblique est une droite de la forme AX + B à laquelle une fonction se rapproche ou s'éloigne à l'infini. Pour simplifier l'étude d'une fonction comportant une asymptote oblique, on peut séparer les différentes fractions qui la composent. Par exemple, si on a 2X, il est possible de simplifier cette expression en fractions distinctes, ce qui facilite la compréhension et l'étude de la fonction. Il est important de bien maîtriser ce concept, car il peut être abordé dans un exercice et devient un exercice classique en terminale. L'exercice consiste à étudier la variation et les limites de la fonction, et à identifier les asymptotes verticales et horizontales. Pour ce faire, on peut calculer la dérivée de la fonction et observer son signe. Il est également nécessaire de calculer les limites de la fonction aux extrémités de l'intervalle d'étude. Enfin, il est important de bien séparer les cas d'approche de zéro par la droite et par la gauche, afin de repérer d'éventuelles erreurs de calcul. Une fois toutes ces étapes complétées, il est possible de déterminer les asymptotes et de réaliser l'étude de la position relative de la fonction.
Révisions Maths lycée
Analyse Terminale
ECG
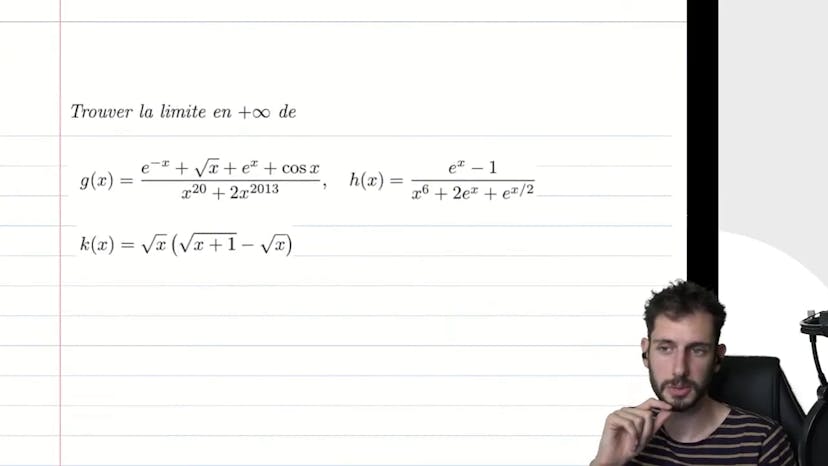
Croissance comparée plus lourde
Le cours traite de la croissance comparée et de la façon dont cela affecte le terme dominant d'une expression mathématique. Il explique comment comparer E de x avec n'importe quelle puissance, en mettant en évidence le terme qui semble être le plus grand. En simplifiant l'expression, il est possible d'obtenir 1-E de x. Le cours explique également que E de x tend vers 0 lorsque x tend vers l'infini. De même, l'exponentielle de moins x tend également vers 0 lorsque x tend vers l'infini. En utilisant ces informations, on peut conclure que x6 sur E de x tend vers l'infini lorsque x tend vers l'infini. En résumé, le cours montre la tendance de certaines expressions mathématiques à s'approcher de 0 lorsque la variable tend vers l'infini.
Révisions Maths lycée
Analyse Terminale
ECG
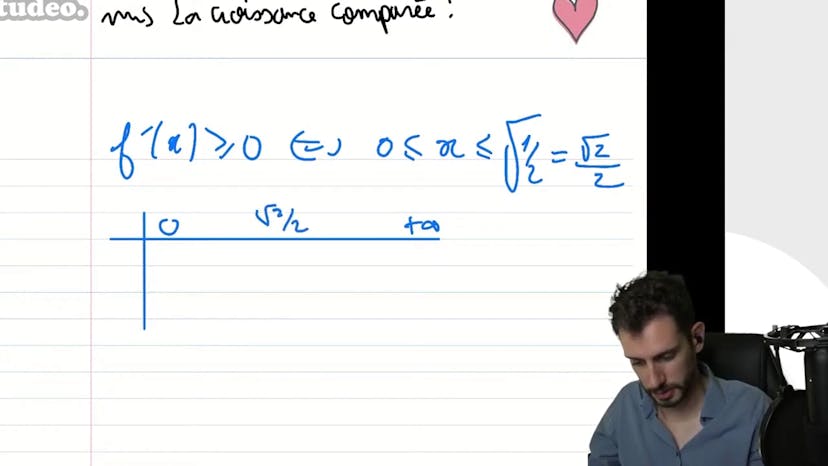
Difficile : BAC 2009
Ce cours est une étude de fonction complète portant sur une fonction donnée. Il commence par trouver la limite de la fonction lorsque x tend vers l'infini, en utilisant le concept de croissance comparée. Ensuite, il montre que la fonction admet un maximum en une certaine valeur, en calculant sa dérivée et en analysant ses variations. Il conclut en donnant les valeurs de la fonction aux points critiques.
Révisions Maths lycée
Analyse Terminale
ECG

Exp : indéterminée en -∞
Le cours propose une démonstration mathématique et une étude de variations pour la fonction F(x) = x * e^(2x). Le professeur rappelle une limite connue (limite de e^(2x)/x tendant vers +∞) et utilise cela pour simplifier l'exercice. Il détermine ensuite la limite de F(x) quand x tend vers +∞ et conclut que F(x) a une asymptote horizontale à y = 1. Il admet également que F(x) est dérivable sur R et calcule sa dérivée qui est F'(x) = (x+1)e^(2x) - e^(2x). En étudiant les variations de F', le professeur montre que F'(x) est positif ou nul lorsque x est inférieur ou égal à -1, et négatif lorsque x est supérieur à -1. Il reprend ensuite les limites trouvées précédemment pour conclure que F(x) admet une asymptote horizontale à y = 1 et qu'il y a un point d'inflexion au point (-1,0). Une petite erreur est corrigée à la fin du cours.
Révisions Maths lycée
Analyse Terminale
ECG

Vers la SUP : Quantité conjuguée
Dans ce cours, nous avons une somme avec un nombre fini d'éléments. La variable x tend vers l'infini, tandis que le nombre de termes dans la somme, noté n, reste fixe. Nous remarquons également la présence de racines avec un signe moins, ce qui nous fait penser à utiliser la quantité conjuguée. En utilisant cette astuce, nous pouvons regrouper les termes de la somme de manière à avoir une racine de x plus 1 moins une racine de x, puis une racine de x plus 2 moins une racine de x, etc. Après cela, nous pouvons simplement multiplier chaque terme par une quantité qui nous intéresse, à savoir racine de x plus 1 plus racine de x, divisé par la même quantité, afin de simplifier l'expression. Finalement, nous obtenons une identité remarquable où chaque terme tend vers 0 lorsque x tend vers l'infini, ce qui nous permet de conclure que la somme dans son ensemble tend également vers 0. La clé pour résoudre cet exercice réside dans la capacité à surmonter les peurs liées à l'écriture, à ne pas confondre x avec n, et à réfléchir calmement en utilisant les connaissances et astuces apprises précédemment.
Révisions Maths lycée
Analyse Terminale
ECG
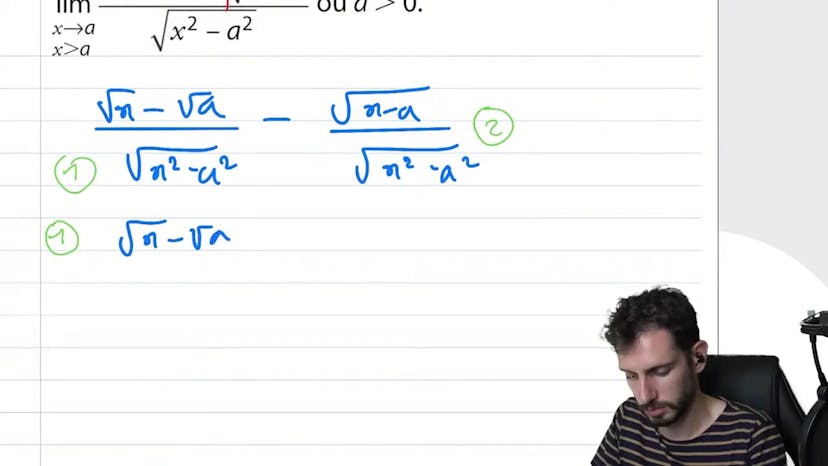
Quantité conjugée piégeuse
Le sujet abordé dans ce cours est l'utilisation des quantités conjuguées dans le calcul mathématique. L'orateur explique que l'utilisation de quantités conjuguées peut conduire à des erreurs si elles ne sont pas correctement appliquées. Il présente une méthode pour résoudre des équations complexes en séparant une fraction en deux parties et en utilisant des quantités conjuguées pour simplifier les calculs.
L'orateur divise la fraction en deux parties et nomme ces parties "1" et "2". Il commence par résoudre le "bloc 1" en utilisant une quantité conjuguée. Il simplifie les calculs en utilisant des propriétés de la racine carrée et démontre que lorsque x tend vers a, le résultat tend vers zéro.
Ensuite, l'orateur aborde le "bloc 2" qui est moins complexe que le premier. Il utilise les résultats obtenus dans le bloc 1 pour simplifier les calculs et conclut que la fonction f(x) tend vers -1/(2racine(x)) lorsque x tend vers a.
En résumé, ce cours explique comment utiliser des quantités conjuguées pour simplifier des calculs mathématiques complexes. L'orateur divise une fraction en deux parties, résout une partie en utilisant une quantité conjuguée, puis utilise ces résultats pour simplifier la deuxième partie de la fraction. La méthode présentée permet de résoudre des équations avec des racines carrées et d'obtenir des résultats plus simples et plus précis.


